基于IT2SFNN 的多关节机械手自适应反演控制*

马欢欢 赵乐

（贵州大学机械工程学院 贵阳 550025）

1 引言

在智能制造时代，机械手兼具人和机械的优点，被广泛应用于汽车制造和航空航天等诸多领域，如何控制机械手的高效运作成为一个研究热点［1～3］。但机械手在作业过程中，运动状态不断变化，具有时变性；内部摩擦和未知干扰的存在又使机械手具有一定的不确定性，因此在模型模糊的前提下，传统的控制方法和手段很难使机械手关节在快速追踪到期望轨迹的同时保持良好的控制精度。

为了取得理想的控制效果，人们尝试将更多的控制方法引入到机械手系统中。PID 控制器由于成本低、结构简单和良好的控制性能被采纳［4～6］，但由于机械手为强非线性的系统，而PID 控制器更好地适用于线性系统和微非线性的系统，因此这类方案的控制效果并不理想。鉴于此，计算力矩的非线性控制器、自适应控制和滑模控制等非线性控制方法被应用于机械手系统。W.Peng等针对机械手设计的非线性控制器性能良好［7］，但该控制器是建立在足够精确的模型之上的，而机械手在实际工作过程中，参数时刻变化，模型十分模糊，因此该设计方案有一定的局限。滑模控制针对时变性和非线性的机械手系统，表现出良好的控制性能［8～10］，但是其存在抖振的问题，可能激发机械手建模中被忽略的高频动态，从而导致系统崩溃。自适应控制因其抗干扰等优点在多关节机械手控制中应用广泛［11～13］。

近些年，自适应反演法作为控制不确定非线性系统的有效工具被引入到机械手控制系统［14～15］。但是模型的不确定性以及未知的扰动为反演控制带来了难题。神经网络的出现很好地弥补了这一缺陷，改善了反演控制的性能。由于神经网络具有逼近任意非线性函数的优点，因此被广泛应用于逼近机械手模型中的惯性力矩阵和离心力与哥氏力等。二型顺序模糊神经网络（T2SFNN）作为模糊理论与神经网络的产物，兼具二者的优点［16］，表现出更好的学习能力。

基于上述学者对机械手的研究成果，在反演控制框架内融入神经网络，利用区间二型顺序模糊神经网络（IT2SFNN）处理机械手干扰未知和模型模糊的问题，在此基础上采用反演控制方法设计控制器，并针对未知干扰项和逼近误差设计了鲁棒补偿项以获得更理想的控制效果。

2 动力学模型

多关节机械手的动力学模型可表示为如下非线性微分方程［17］：

机械手的动力学模型具有以下特性［18］：

3）未知扰动τd满足‖τd‖≤τM，τM为一正常数。

随着机械手关节数目的增加，其动力学模型的耦合性和非线性增强。另外，动力学模型的时变性和不确定性为实时获取精确的模型参数带来了困难，这里将利用IT2SFNN来解决这个难题。

3 IT2SFNN

本节对IT2SFNN［16］进行介绍。IT2SFNN 结构如图1 所示，共有5 层：输入层、模糊化层、隶属度层、模糊规则层和输出层。

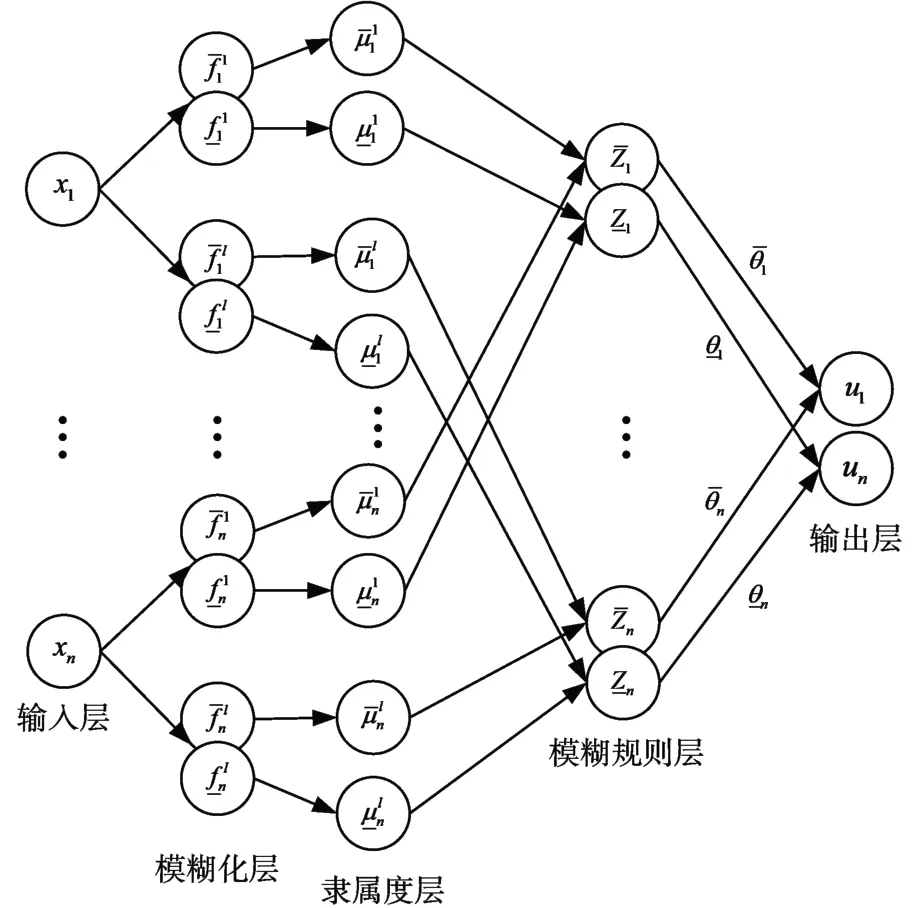
图1 IT2SFNN结构图

隶属度层：此层对上层的输入值继续进行模糊化处理，采用区间二型高斯隶属度函数，如图2 所示。与fi相对应的高斯型上限隶属度函数和高斯型下限隶属度函数分别为

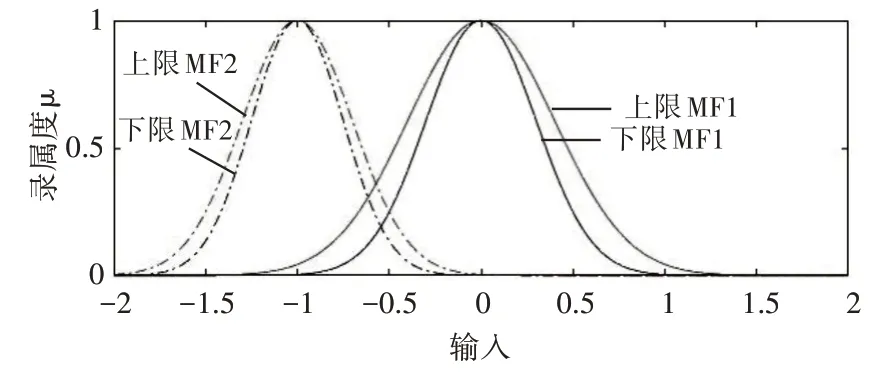
图2 区间二型隶属度函数

模糊推理层：IT2SFNN 中的模糊规则设计如下：

输出层：IT2SFNN 的输出值u取上限输出与下限输出的平均值即：

4 控制器设计

为了解决上述提到的问题，基于自适应反演法分三步设计控制器，使机械手各关节在快速进入期望轨迹的同时保持高的控制精度，取得理想的控制效果。

第一步：定义跟踪误差为

式中，qd为期望跟踪角度。

定义第一个Lyapunov方程为

第二步：令

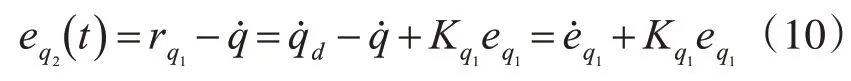
分别对式（9）和式（10）求导得

对式（14）求导得

式中：

第三步：设计控制输入

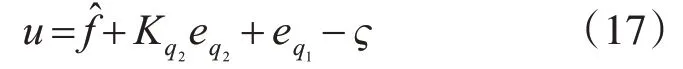
式中ς为针对IT2SFNN 逼近误差ε和不确定干扰τd设置的鲁棒补偿项。将鲁棒补偿项ς设计为

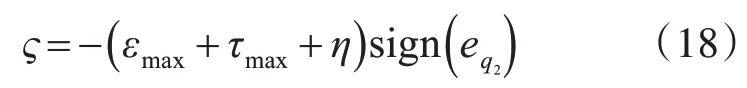
其中‖ε‖≤εmax，‖τd‖≤τmax，η＞0。

将式（17）代入式（15）得

定义θo为理想逼近常量，θ为实际逼近常量，令-θ。

定义第三个Lyapunov方程为

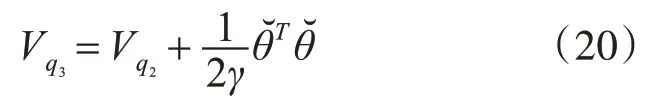
对式（20）求导得

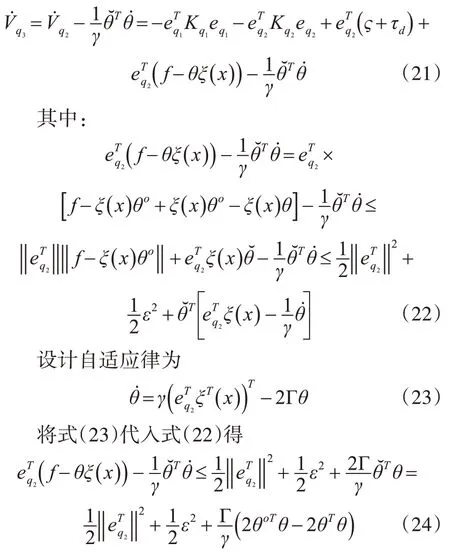
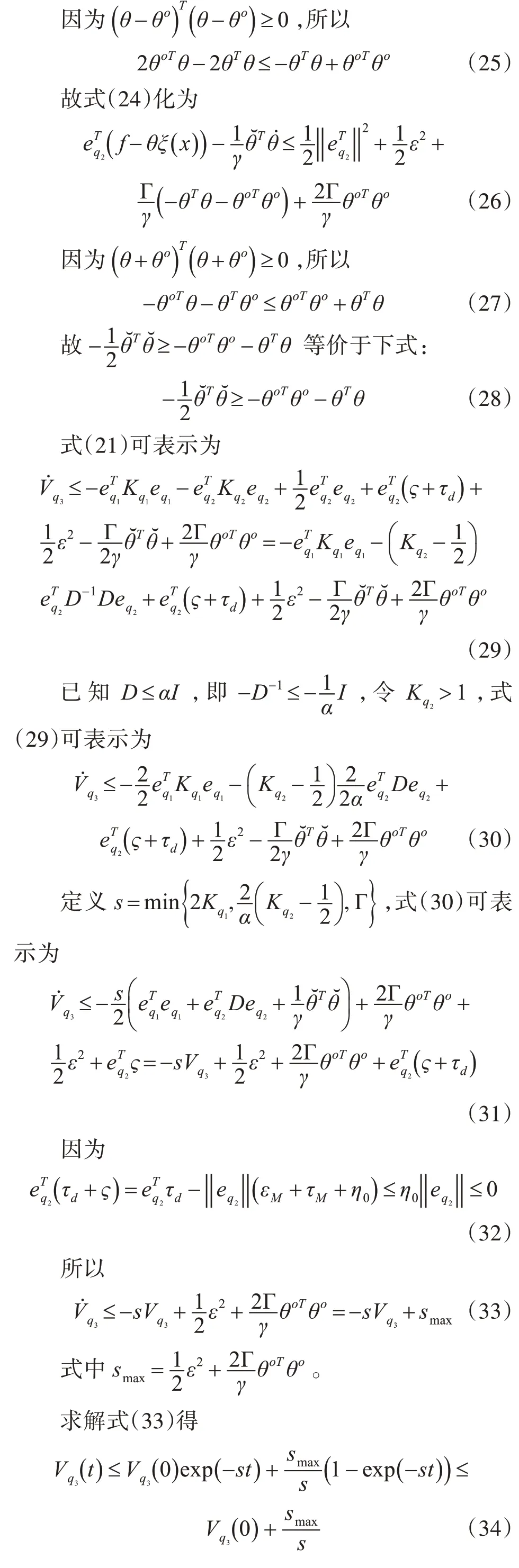
5 数值模拟

这里以二关节机械手为仿真对象，模型中

5.1 位置跟踪分析

图3 为两关节的位置跟踪仿真结果，从中可以看出，所设计控制器能使关节1 和关节2 在0.1s 内跟踪到期望的位置信号，快速进入理想轨迹，足以达到大部分机械手的工作要求。图4 为两关节的跟踪误差，从中可以看出，系统达到稳态后，关节1的跟踪误差可以稳定在0.01rad以内，关节2的跟踪误差可以稳定在0.005rad 以内，表明所设计的控制器具有良好的控制精度。

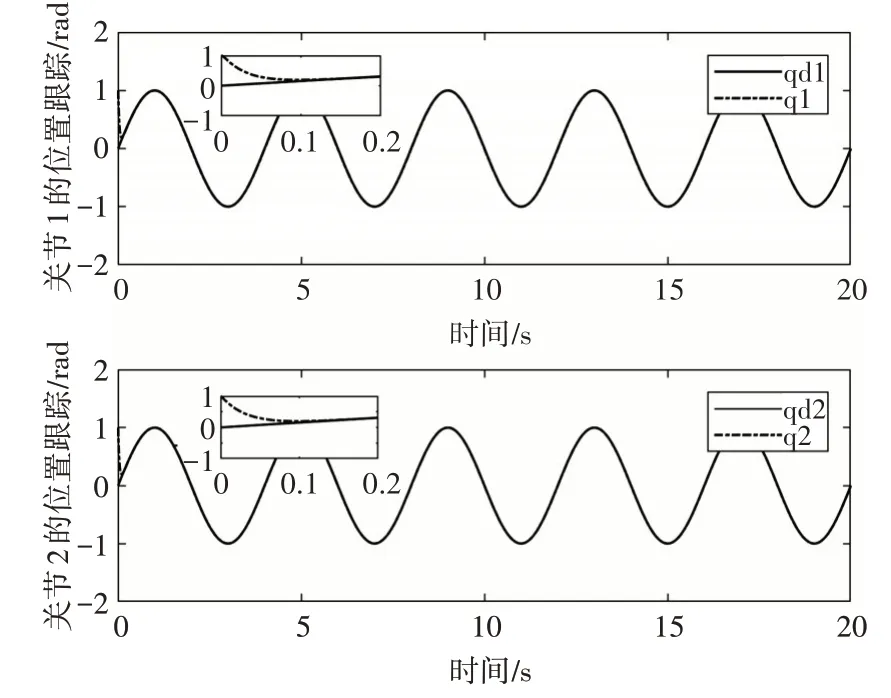
图3 位置跟踪

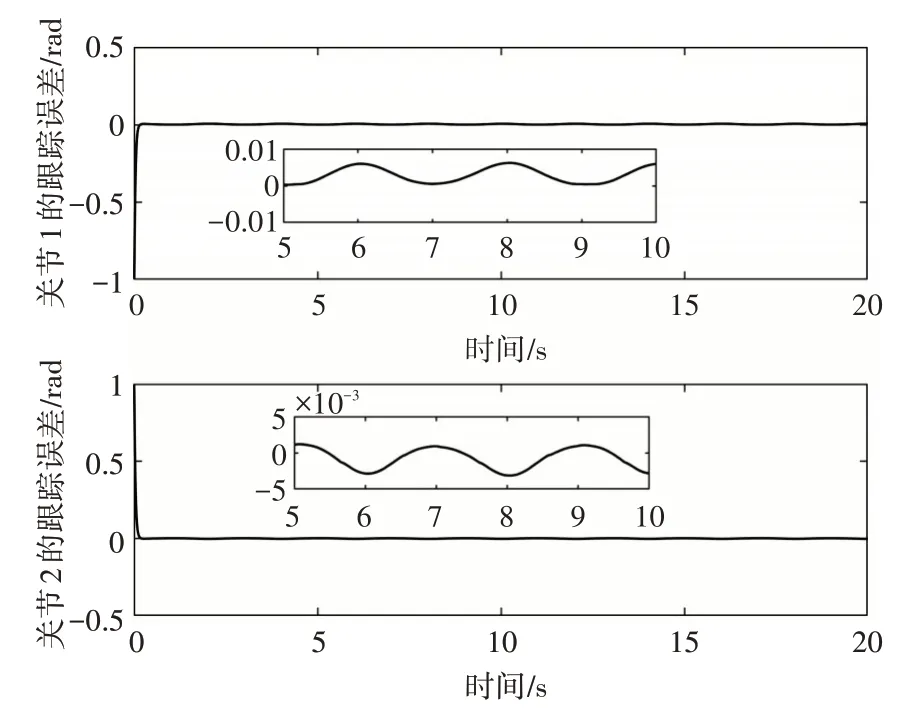
图4 跟踪误差

5.2 鲁棒性分析

仿真过程中，分别取干扰τd1=[0.4 sin(t) 0.4 sin(t)]T，τd2=[0.15 sin(t) 0.1 5 sin(t)]T与τd=[0.25 sin(t) 0.2 5 sin(t)]T时的跟踪误差和控制输入作比较，得到图5和图6。从图中可以看到，随着干扰力矩的变化，两个关节的跟踪误差维持在极小的变化范围内，控制输入也仅有微小浮动，即表明所设计的控制器对于不同的外界干扰表现出较强的鲁棒性。

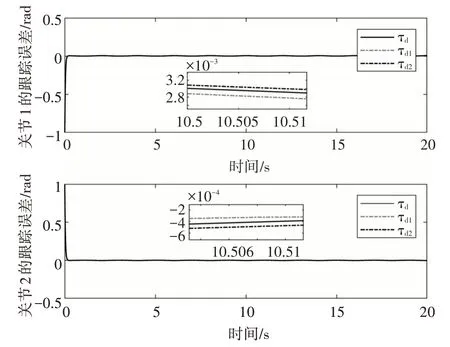
图5 不同干扰下的跟踪误差

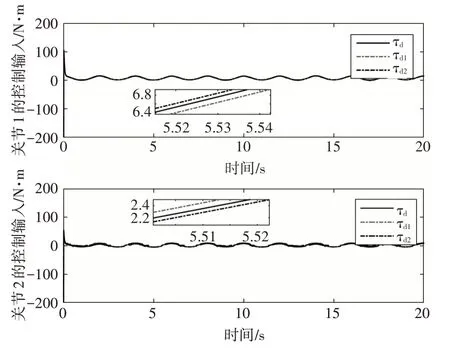
图6 不同干扰下的控制输入

6 结语

结合多关节机械手时变性和不确定性的特点，提出了一种自适应的反演控制策略。利用IT2SFNN 获取机械手模型中不确定部分的估计值，基于李亚普诺夫稳定性理论设计了控制律和自适应更新律，并且在保证闭环系统稳定性的前提下，设计了鲁棒补偿项。仿真表明，所设计的控制器能保持良好的控制精度并快速跟踪到期望信号，且鲁棒性良好。