基于图像分割和对抗训练的去雾算法*

谢勇 贾惠珍 王同罕 雷初聪 徐铠珈

（1.东华理工大学江西省放射性地学大数据技术工程实验室 南昌 330000）（2.宁波大学计算机科学技术研究所 宁波 315211）

1 引言

由于气候变化或者空气污染，不可避免地产生含雾图像。然而，图像质量的各个方面都容易因雾的存在而退化，尤其是在颜色和纹理等方面容易被影响，从而造成图像的模糊失真等问题。近来，为了解决这类问题，许多学者在雾图去雾方面做出了巨大努力，许多经典的算法也孕育而生。现今，主要可分为如下两种典型的图像去雾方案。

基于特征和先验，这类去雾方法往往侧重于对透射图的估计，这不可避免地使特征和先验的选择成为一个难点。有以下三种典型的雾图特征和先验：1）对比度。Tan［1］在统计中发现，相比于含雾图，无雾图像在对比度方面的数值是较高的，于是利用实现含雾图像的局部对比度最大化进而实现对含雾图像的去雾处理。2）暗通道先验。在实验中，He［2］发现，无雾图像的暗通道几乎为零，于是将暗通道作为估计透射图的工具，并且利用大气模型重新计算构造无雾图像，从而实现除雾。3）颜色衰减先验。在前人的基础上，Zhu［3］发现并利用雾的浓度与其亮度减去其饱和度的值是成正比这一规律，引入基于场景深度（景深）的线性模型来解析雾图景深，从而重新计算构造无雾图像。

基于学习的去雾方法，按照学习方式的不同，分为基于分步学习去雾算法和基于端到端学习的去雾算法。对于分步学习的去雾算法，其与传统的去雾方法相似，对通过预测得到的中间变量依赖性强。例如，Cai［4］对人工先验特征分析，针对性地设计了DehazeNet 模型，从而实现对透射图的更加准确预测。无独有偶，Ren［5］也构建了一种用于精准预测透射图的多尺度的卷积神经网络（MSCNN），其利用两个不同尺度的神经网络模型精准实现透射图的预测。由于上述算法都忽视了预测的大气光值的合理性，Li［6］利用线性变化，对大气散射模型［7］进行重构，将模型的多个中间变量融合成一个等价的变量，从而进一步引出了AOD_Net［6］，以实现无雾图像的直接预测。

很多图像处理工作均可看作是多个图层的混合与分离问题。例如，当图像受雾影响，我们可以将其视为两层的混合物：一层是没有雾的背景层，另一层是雾层。GAN 在零和博弈中网络内部不断相互对抗优化，从而达到生成更加真实的假图像的同时实现对真假图像的识别。在此基础上，受深度对抗分解［10～14］的启发，本文提出了一种基于图像分割和对抗训练的去雾算法，在参数训练时，其首先将一张清晰图和一张雾图作为输入，随机进行线性或者非线性图像融合，得到一张含雾的混合图。其次，引入一个分离器将之再次分离成新的清晰图和雾图，利用两张原图和分离之后的两张分离图，利用交叉计算误差作为损失函数，对分离器进行训练优化，充分学习雾图特征。再者，引入一个鉴别器，对分离器处理完之后的图进行鉴别，鉴别混合图分离与否。在整个训练过程中，保证最小化分离器误差的同时，实现鉴别器鉴别率的最大化。在去雾时运用训练得到的模型，对雾图通过图像分割，从而达到去雾的目的。

2 相关工作

2.1 大气散射模型

常用大气散射模型［7］来对雾图的成像原因进行描述，对其公式重写如下：

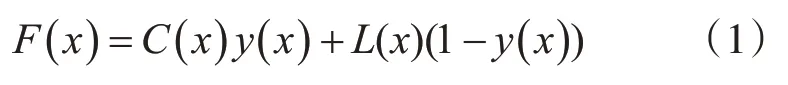
式中，F(x)，C(x)，A(x)分别代表雾图，无雾图，大气光值。y(x)代表各像素的透射率，x则代表整幅图像的每一个像素的位置。

假设大气成分是均匀，即L(x)不变时，那么则可对透射率y(x)重写为

其中，β，d(x)分别代表大气衰减系数，景深。

显而易见，该模型去雾效果受景深和大气光值的影响较大。在去雾过程中，仅雾图对研究人员是已知的，对于透射图和雾气的分布，研究人员很难对其进行预测，而且对于透射图以及雾气的不准确估计也可能导致误差的累积，很容易导致最终的去雾结果达不到预期。

2.2 生成对抗网络及其改进

生成对抗网络（即GAN）是一种深度学习模型，由Goodfellow 等［14］设计提出。GAN 主要由两部分组成，一个生成器G，一个判别器D。基于零和博弈的思想，生成器G试图在生成样本时获得尽可能真实的结果，同时判别器D尽可能将样本生成与真实样本更加精确地区分开来，即尽可能区分假图和真图。起初，GAN 刚现世的时候，以生成具有良好感知质量的图像而名噪一时，但模型坍塌以及梯度分散等问题仍存在，并没有没有得到有效解决。为了解决以上问题，Arjovsky 等［13］提出衡量不相交部分之间的距离时，JS 散度并不适用，从而利用Wasserstein 距离W(q,p)对生成样本和真实样本的距离进行衡量，由此进一步提出了称为WGAN 的GAN 的改进版本。对于WGAN 的损失函数，可具体表示如下：

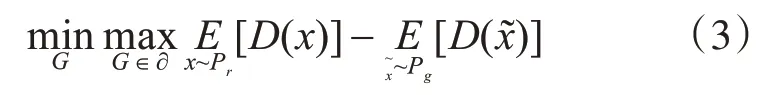
其中，∂代表一组非线性函数（满足利普希茨连续），Pg代表生成样本的数据分布，Pr代表真实样本的数据分布，训练WGAN 时，判别器D 遵循利普希茨函数的连续性，从而使判别值约等于K*W(Pr,Pg)，K代表利普希茨常数，规定了判别器梯度值的上限，W(Pr,Pg)则代表Wasserstein 距离，在WGAN 网络训练时，判别网络的权值被规定为[-c,c]，通过这一方式，权值参数的界限得以确保，从而限制其梯度信息。

3 本文算法

本文算法训练流程及去雾流程如图1、图2 所示。在训练时，输入的清晰图与雾图首先进行基于稀疏表示的图像融合，融合混合之后的图像进入分离器D，通过计算交叉计算损失，进入鉴别器C，以判别混合图像分离与否，同时鉴别器C 也在训练过程中参加训练，不断优化模型参数，使分离器D 最小化的同时鉴别器C 最大化。通过训练得到的分离器模型对雾图进行处理，实现去雾。

图1 训练流程

3.1 图像融合

在对图像进行图像分割训练前，本文算法利用基于稀疏表示的图像融合对雾图和原图进行融合。融合框架如图2所示。

图2 去雾

3.1.1 高频部分融合

由左向右，由上自下，将图像分为m*m个像素块，用一个单独的矢量代表一个像素块，用矢量v1和v2 表示大小为A*B的源图像x1 和x2，矢量的大小则表示为m2((A-m+1)(B-n+1))。每个矢量的稀疏表示则是通过OMP 算法实现。从而得到用来表示v1 和v2 的稀疏矢量v11 和v22 。v11 和v22 的融合规则为当列矢量对应的1范数都是最大值时，对应的列矢量即为融合列矢量V，则：

融合后的雾图y的矢量可表示为

其中，Z为已经学习过的字典原子。

最后，融合图像通过y进行重构。将V中的每一列矢量逐步归位，融合恢复成m*m的图像块。对于重构的图像，重构像素值为几个块值之和，最后比上叠加次数得出高频部分的融合图像。

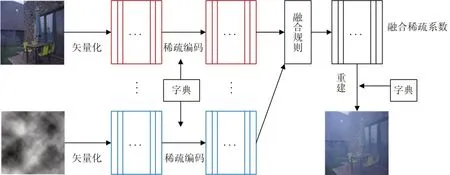
图3 融合框架图

3.1.2 低频部分融合

低频部分较高频部分的融合方式稍简单一些，即取各系数绝对值的最大值为融合后的稀疏。最终得出融合后的雾图可表示为

其中，f(.)表示图像融合。

3.2 分离器

分离器进行图像分割，实现去雾，如图4所示。

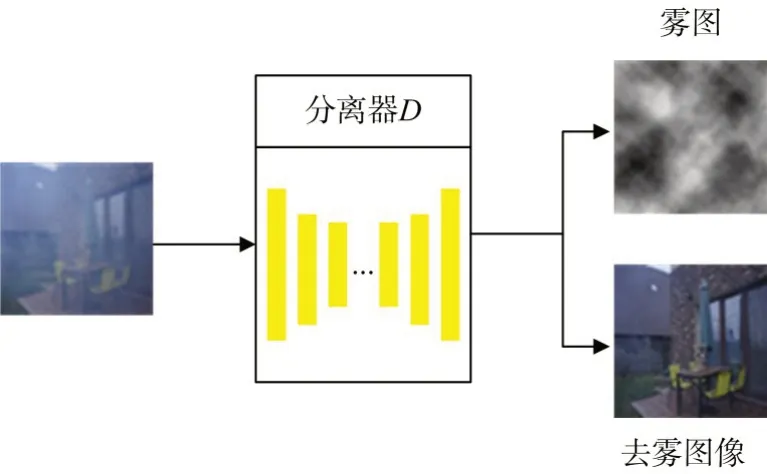
图4 图像分割实现去雾

以下部分，主要对本文分离器损失函数进行介绍。

这一部分是本文算法的核心，通过分离器D 对进行图像融合之后的雾图进行图像分离，得到分离之后的图像x11 和x22，对于x11 和x22 的输出顺序本文算法没有进行特殊规定，即分离器D分离出来的图片x11 和x22 输出顺序是随机的，本文算法在计算源图像x1，x2 与分离器D 分离出来的图像x11，x22 的损失时，应该将所有的输出情况考虑在内，即交叉计算：(||x11-x1||1,||x22-x2||1) 以及(||x11-x2||1,||x22-x1||1)。在对抗训练中，损失函数进行迭代优化，充分学习雾图特征，使其分离参数取得损失的最小值。即：

则整个数据集上的损失为

其中，xi（i=1，2，3，…）代表图像集中的所有图像。

3.3 鉴别器

基于图层具有不可避免的模糊性，分离器D 没有利用手工约束以及基于数字统计的约束，而是通过对抗训练，不断学习优化分离器D。为了进一步鉴别经过分离器D处理之后的雾图分离与否，引入一个鉴别器C，鉴别器C 不考虑经过分离器D 进行分离处理得到的两个输出图像的顺序，通过训练来实现区分输出(x11,x22)和一对源图像(x1,x2)，损失函数L进一步具体表达为

其中xi（i=1，2，3…）为图集的所有图片，xii 为分离之后的图片（即x11，x22）。值得一提的是，在鉴别器C 输入的末端，只是简单地将分离器D 分离出来的两张图片x11 和x22 在通道维度上简单的进行连接，以此来模拟分离出来的两张图片的联合概率分布。从而表现出分离器D 与鉴别器C 在对抗训练中不断最小化分离器误差的同时，实现鉴别器鉴别率的最大化的过程。在图像进行图像融合，分解，加权平均以及分离器D 鉴别器C 对模型进行充分训练之后，充分学习得到雾图的特征。概括得出最终结果：

4 实验与结果分析

4.1 图像库和评价标准

为了验证本文算法的有效性，训练及实验时均使用RESIDE［16］数据集，在定性与定量两个层面上，本文算法与现在较为经典的去雾算法进行实验比较。在客观评价指标的选用上，使用峰值信噪比（PSNR）和结构相似性（SSIM）作为评价指标。PSNR 反映的是图像结构信息完整性程度，显而易见，其数值越大，即代表图像的完整性程度越高，即噪声对图像的影响也就越小。SSIM 反映的是图像结构的相似性，其数值越大，即代表相似性程度越高，即失真程度也就越小。

4.2 算法性能比较

在设计分离器D 时，本文算法使用了UNet［15］。在分离器D 中，本文算法没有进行批量归一处理，显然本文算法工作量得以大大减少，提高了效率。同时为了提高效率，本文算法没有采取增加网络层数的方式，而是将通过鉴别器C 处理之后得到的输出图像尺寸进行调整，设置一个相对较小的值：64*64，用来捕捉整幅图像。在构建鉴别器C时，用4*3 全卷积作为标准的FCN。在默认参数的设置上，使用batch_size=2，learning_rate=e-4 的Adam优化器，并训练200epochs。

4.2.1 主观视觉效果对比

本文算法与经典去雾算法［19，21～22］实验对比结果如图5 所示。显而易见：对于室内图像，从人眼主观视觉上即可很直观地看出，DCPDN［19］、EPDN［21］、文献［22］算法均或多或少存在颜色扭曲、色彩失真、块效应等问题，在很大程度上并没有实现去雾，反而加重了含雾图像的模糊程度，去雾效果不佳。反观本文算法的去雾结果，可以直观看出，去雾之后的图像在纹理结构上保真度较高，更加清晰自然，对于室内和室外雾图的去雾处理，均有相当优秀的去雾效果。

图5 主观视觉效果对比

4.2.2 客观性能指标对比

通过含雾图像与处理之后得到无雾图像进行对比，使用PSNR和SSIM这两种客观评价指标来评判图像去雾处理之后的效果。实验结果如表1 所示。

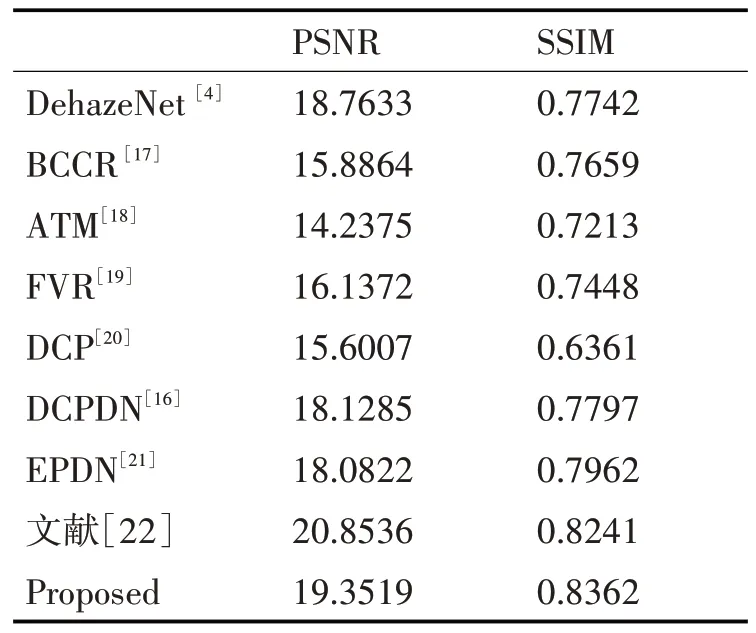
表1 客观性能指标对比

由表1 可知，相比于现存的一些经典的去雾算法，在SSIM 指标上，本文算法的数值较高，说明去雾前后的图像在结构上本文算法更为相似，在图像纹理细节保持方面表现更加突出；另外，在PSNR指标上，本文的去雾算法也明显占有优势。这说明经过本文算法在像素级上进行去雾之后的图像与原始的不含雾的清晰图像差异小，噪声对处理之后的图像的影响更小，去雾处理之后的图像更加清晰真实。

4.2.3 时间复杂度对比

本文算法同上述较为经典的去雾算法，同时对75 幅相同雾图进行去雾处理，平均去雾耗时定义为75 幅雾图去雾总耗时比上图像总数量得到平均去雾时间（s）。本文实验硬件环境和软件环境，硬件环境：CPU：Intel（R）Core（TM）i5-6300HQ CPU@2.30GHz；GPU：NVIDIA GeForce GTX 950M；内存：8GB；软件环境：64bit Windows10；Anaconda3-5.3.1；python 3.6。由表2 可知，本文算法在去雾时间上相对而言效果较好，对于对响应时间要求较高的应用领域实用性较强。

表2 去雾时间对比

5 结语

本文提出了一种基于图像分割和对抗训练的去雾算法，在参数训练时，其首先将一张清晰图和一张雾图作为输入，随机进行线性或者非线性图像融合，得到一张含雾的混合图。其次，引入一个分离器将之再次分离成新的清晰图和雾图，利用两张原图和分离之后的两张分离图，利用交叉计算误差作为损失函数，对分离器进行训练优化，充分学习雾图特征。再者，引入一个鉴别器，对分离器处理完之后的图进行鉴别，鉴别混合图分离与否。在整个训练过程中，保证最小化分离器误差的同时，实现鉴别器鉴别率的最大化。通过训练得到的分离器模型对雾图进行图像分割，实现去雾。实验结果表明，与经典的去雾算法相比较，在主观视觉效果和客观指标上，本文提出的算法都处于现存算法的前列，而且本文算法时间复杂度较低，实用性更强。但本文算法稳定性还有待改进，这是下一步工作的重点。