PSO-LS：一种非视距环境下目标定位方法*

金超 汪 洋

（1.武汉邮电科学研究院 武汉 430070）（2.南京烽火天地通信科技有限公司 南京 210019）

1 引言

近些年的研究中定位问题的测量和距离估算技术已初步成熟。定位测量模型主要分为距离测量技术和角度测量技术（Angle of Arrival，AOA）等。在基于测距的定位模型中非视距（Non-Line Of Sight，NLOS）误差是影响定位精度的关键因素，而非视距误差由于其统计特性不稳定，常常给定位精度带来较大影响。

如果目标和所有信标节点之间信号进行视线传播（Line Of Sight，LOS），则可以获得较高的定位精度。然而，在从目标到信标的直接路径被障碍物阻挡的情况下，信号测量行进中的过量路径导致的测量误差使得定位精度受到影响，该误差被称为NLOS误差。

非视距误差目前主要研究方向有非视距传播的识别、非视距传播误差的抑制、非视距传播的利用及非视距场景下的定位方法设计四个方面［1～2］。本文主要的研究方向为非视距场景下的定位方法设计。

在NLOS 环境下进行定位，有NLOS 判别、鲁棒求解定位位置、利用启发式算法定位求解等几种方案。针对NLOS 和LOS 混杂环境，文献［3］提出使用到达时间差（Time Of Arrival，TOA）和AOA 结合的NLOS 识别方法，文献［4］通过Anderson-Darling检验进行NLOS判别，从而区分LOS和NLOS。

鲁棒求解定位位置无需知道任何距离模型的参数，也不需要任何关于NLOS 测量的统计属性先验信息。文献［5］针对线性最小二乘方案中隐含无误差测量假设问题以及其半定松弛（Semidefinite relaxation，SDR）解的不稳定性，提出使用平方距离测量的方案，通过将原定位问题转换为广义信任域子问题（Generalized trust domain subproblem，GTRS）进行求解。文献［6］在此基础上进一步证明了该方案对NLOS 误差抑制的有效性，该文使用距离倒数加权的方式对测量距离进行加权处理，从而达到抑制NLOS 误差的效果。文献［7］使用二等分法求解GTRS，提升了模型定位的精度。文献［8～10］分别从两步加权最小二乘、基于中位值的最小二乘、使用模糊加权的最小二乘等方面对NLOS 定位误差进行限制。然而，基于鲁棒最小二乘方法的定位计算往往需要通过多个测量点的多组测量位置来提高测距精度且其计算量相对较大。

同时使用启发式算法求解目标位置的方法得到了部分学者的重视。文献［11］通过遗传算法使用一组测距信息对目标位置进行快速计算，但由于只使用单次信息，对于非视距环境的定位效果不佳。针对于该情况文献［12］在非视距情况下使用均方根时延拓展模型对TDOA 测量误差纠正，再通过最小二乘获得近似解，使用粒子群算法得出最优解，文献［13］在NLOS 环境中使用粒子群算法，利用惯性权重的非线性调整策略进行定位。

由此，本文提出一种NLOS 和LOS 混合环境中的目标定位算法，首先通过AD 判别筛选出NLOS较小的测距结果，再通过粒子群算法得到目标位置初值，最后通过迭代最小二乘得到目标最终定位位置。仿真效果表明本文算法在较小计算量的情况下，提升了定位的精度。

2 PSO-LS算法

粒子群优化算法［14］（Particle Swarm Optimization，PSO）由Eberhart和Kennedy 于1995 年提出，是一种基于种群的随机优化技术。PSO 模拟自然界中昆虫、鸟群、鱼群等的群集行为，这些群体按照一种合作的方式寻找食物，群体中的每个成员通过学习自身经验和其他成员的经验来不断改变其搜索模式。

迭代最小二乘［15］（Iterative LS，ILS）是求解非线性最小二乘逼近问题的，可以用来作为目标定位的方法。通过不断的迭代逼近目标位置。

Anderson-Darling test 通过对数据分布判别分析达到LOS 和NLOS 区分的效果。在得到一组测距数据后进行AD检验。检验结果符合要求则表明该组数据近似服从正太分布，可将该组测距视为近似LOS条件下测得，不符合要求则说明该组数据可视为在NLOS条件下测得。整体算法框架如图1所示。

女人说完就主动伸出手来，我心里有种莫名其妙的冲动。我赶紧握住女人的手，女人的手很白很嫩，我紧紧地把它攥在手心里，女人并没有反对，好像这白晰修长的手原本就该属于我一样。

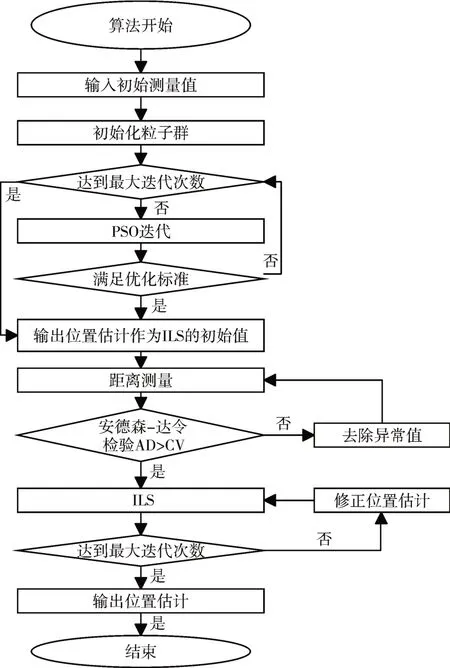
图1 算法流程

2.1 Anderson-Darling test（AD test）

LOS 环境和NLOS 环境下的距离公式如式（1）所示。存在一组测距数据D=[d1,d2,…,di,…,dM]，在视距情况下可近似视为服从高斯分布，而由于非视距误差nnlos的不稳定性，dnlos不服从高斯分布。故可以通过测距数据是否近似服从正态分布区分视距环境和非视距环境。

由于实际情况中非视距误差可能极大地影响测量结果的精度和准确性，通过AD 检验方法［4］对视距和非视距环境进行划分，可以筛选出那些非视距误差较小的一些测距组合，从而达到优化测距的效果。

由此可做如下假设H0:di～N(µ,δ2)，通过对距离进行标准化处理式（2）可得～N(0,1)。将处理结果作为标准化输入进行AD计算得式（3）：

其中φ表示标准正态分布概率密度函数，F(Zj)表示其累计分布函数。评价标准CV计算如式（5）：

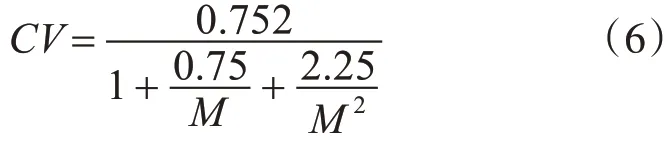
如果AD＞CV，则假设H0错误，说明该组测量距离存在较大非视距误差，需要去除误差较大项并重新测距。否则，将该组测量距离视为近似LOS环境下的测距，进入下一个环节的定位。

2.2 TDOA定位

TDOA 通过测量BS（base station）和MS（mobile station）之间的到达时间差来计算距离差，从而建立双曲线方程。假设存在BS1,BS2,BS3三个定位传感器，我们将其位置定义为x1=(X1,Y1),x2=(X2,Y2),x3=(X3,Y3)。MS 的实际坐标为(x0,y0)，估计坐标为=(x,y)。BSi和BSj到MS的距离差表示为

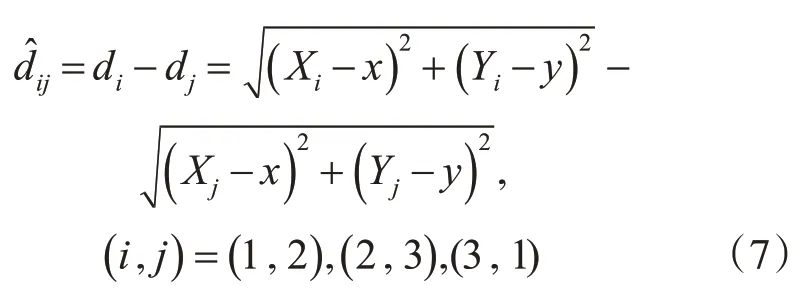
当BS 和MS 之间都是LOS 路径且忽略噪声偏差时，三条双曲线方程将相较于一点，该点就是MS的实际位置(x0,y0)。当噪声偏差和NLOS 误差无法忽略时，三条双曲线将会形成一个称为可行范围的区域，如图2 所示。

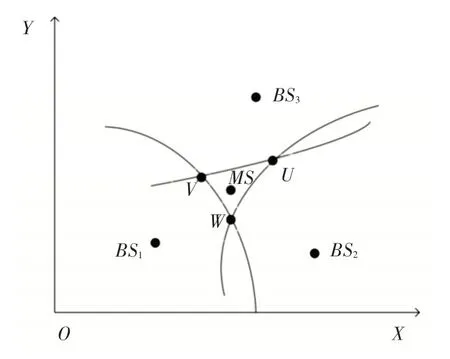
图2 TDOA的可行范围

交点坐标U(Ux,Uy),V(Vx,Vy),W(Wx,Wy)通过求解式（1）中所示的双曲方程得到。PSO 算法中目标函数［16］如式（8）所示：

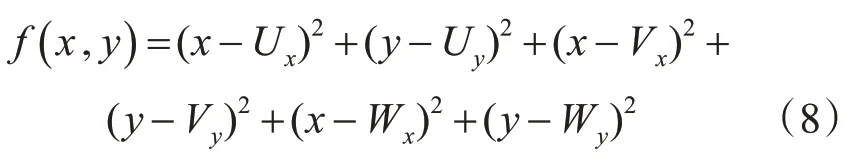
由于MS(x,y)的估计坐标可以在NLOS 误差和噪声偏差引起的可行范围内找到，使得目标函数值最小的解是MS 的估计坐标，于是原本定位问题转换为了带约束最优化问题，求得的估计坐标作为迭代最小二乘的初始值，进入下一步计算。

2.3 迭代最小二乘法（ILS）

上述定位问题中，本文通过测量距离差及实际距离差建立非线性最小二乘，如式（9）所示。以最小二乘结果作为损失函数，通过迭代最小二乘法进行目标定位求解。

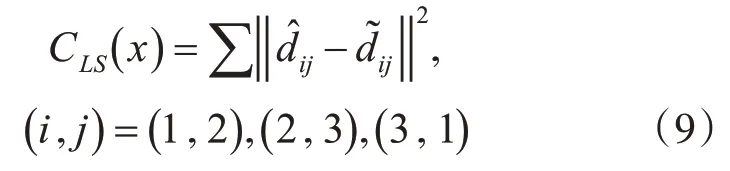
更新迭代公式如式（10）所示：

3 仿真结果分析

3.1 仿真条件

本文采用Python对上述理论进行仿真，仿真环境如下：测量噪声设定为方差为δ2的高斯分布，NLOS 为[0,U]的均匀分布。三个测量点BS 分别位于(0,0)(0,10)(5,)，待测点实际位于(5,5)，且预测位置表示为(x,y)。在得到MS 的估计位置后，根据式（14）计算均方根误差：

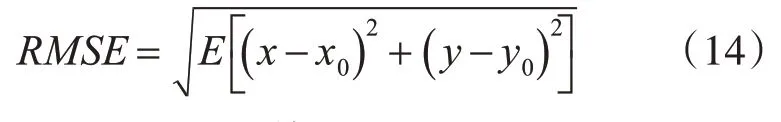
3.2 NLOS环境下不同算法定位效果

图3 展示了在固定迭代步长k=0.01，迭代次数为100 的情况下，不同算法GA、PSO 及ILS 下NLOS误差和RMSE 之间的关系。从图中，可以看出随着NLOS 误差上界的增大，各个算法的RMSE 均逐渐增大。同时，相较于其余算法GA、PSO，ILS 算法的RMSE 值在相同NLOS 误差上界时鲁棒性更强。实验结果表示ILS 可以较大的提升存在NLOS 误差时定位的准确性。相较于GA，PSO 等方法，ILS 算法基于多次测量结果进行定位计算，在测量次数多时定位结果较为准确。然而，ILS 算法虽然对计算精度进行提升，但同时需要更多的计算量及带来更多时延。

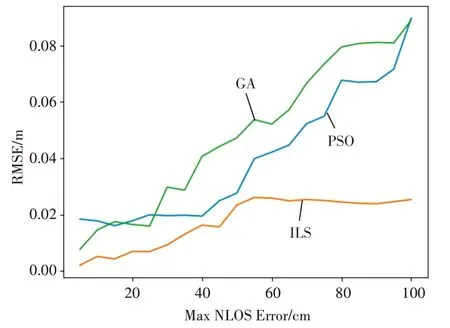
图3 NLOS环境下不同算法定位效果

3.3 不同初值对ILS影响

如图4 所示，使用五个不同点作为初始点运行ILS算法。其中，步长大小设置为0.1，NLOS误差上界设置为50cm，待测点位于（5，5）。在不同初始值下，RMSE 随迭代次数变化的图像如图4 所示。可以看出，随着初始RMSE 误差的增大，收敛时所需迭代次数增加。结果表明初始误差越小，到达相同RMSE所需迭代次数越少。

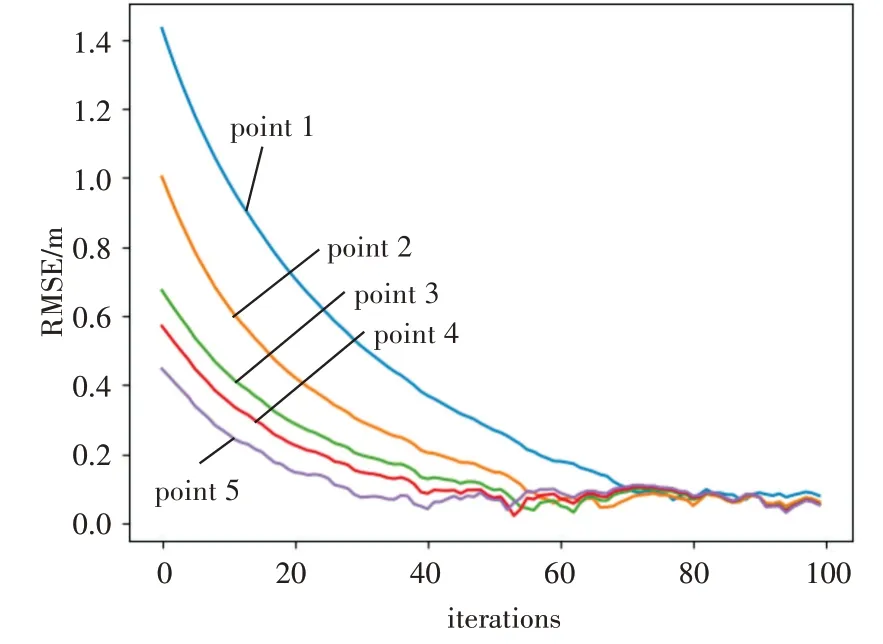
图4 不同初值对ILS影响

表1 显示了到达相同收敛精度时，不同初始点之间的迭代次数关系。从表中数据可见，在RMSE达到相同0.1m 误差时，较大的初始误差将需要更多次的迭代。这一结果展示了选取初始值对于迭代算法的重要性，较为精确的初始值可以较大地减少迭代次数，这对目标定位的实时性有重要意义。

表1 不同初始点达到相同误差迭代次数

3.4 不同步长对PSO_LS影响

由于上述原因，本文提出一种结合PSO 和ILS的新算法PSO-LS。该算法致力于提升定位的准确率的同时减少计算时延。图5 显示了PSO-LS 算法在不同步长下RMSE 随迭代次数变化的变化曲线，实验中NLOS 误差上界设置为50cm。从图中可以看出，步长越大RMSE 收敛越快，但稳定后的精度越低。步长越小，迭代稳定后的RMSE 值越小，但是需要更多的迭代次数。

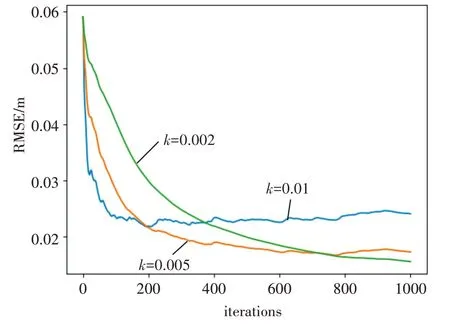
图5 不同步长对PSO_LS影响

结果表明步长需要在定位精度和收敛速度之间进行权衡选择，通过改变步长可以提高定位精度并减少收敛时间。

3.5 可变步长对PSO_LS影响

图6 展示了可变步长k 下RMSE 随迭代次数的变化，可变步长的定义k如下列函数所示：

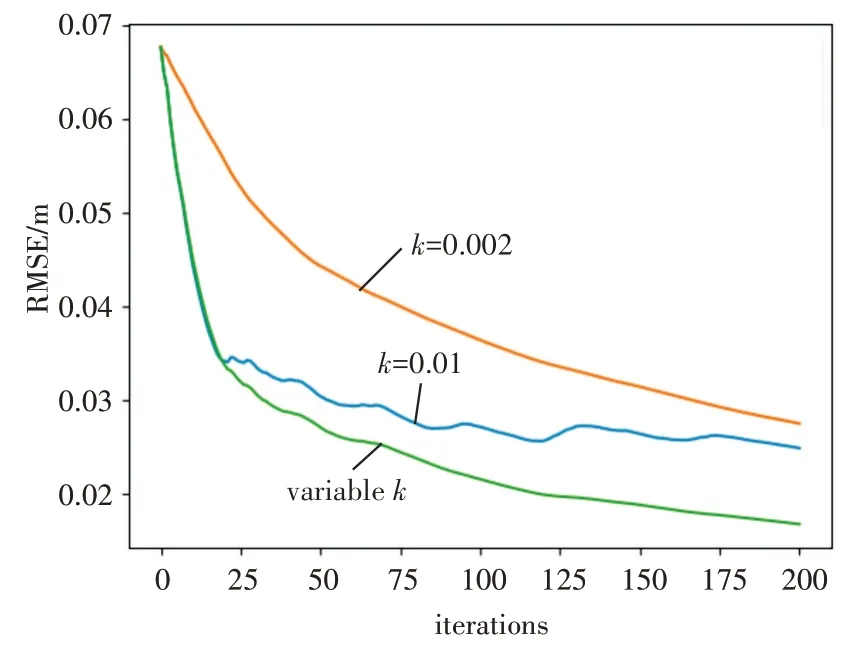
图6 可变步长对PSO_LS影响

其中l表示迭代次数，随着迭代次数的增加，可变步长k(l)随着迭代次数减小。图中展示了步长分别为固定步长0.01、0.002 与可变步长k(l) 时，定位RMSE 误差随迭代次数变化。图中可以看出相较于固定步长0.01，可变步长k(l)可以达到更好的收敛精度。同时相较于固定步长0.002，达到相同定位精度时使用可变步长需要更少的迭代次数。仿真结果表明采用可变的步长选取可以使得收敛速度更快、精度更高。

3.6 非视距环境中PSO_LS定位

图7展示了在不同NLOS上界误差下分别采用PSO 和PSO-LS 算法，在同时迭代50 次后，最终定位误差的结果示意图。图中可以看出，随着NLOS误差上界的增大，粒子群算法的定位误差明显增大，而PSO-LS 算法随NLOS 误差增大定位误差变化相对不明显。结果表明PSO-LS算法可以通过较小的计算量极大地提升定位的准确率。

图7 非视距环境中PSO_LS定位

3.7 混合环境中AD检验对定位改进

图8 展示了在NLOS 和LOS 混合环境中，采用AD检验法对定位性能的提升。仿真实验组数据从150组LOS和150组NLOS数据中提取出满足AD检验的一批数据。对照组采用等比率的LOS和NLOS数据，定位过程均使用PSO_LS 算法。其中NLOS的上界误差设置为100cm。仿真结果表明，在混合环境中的测距采用AD检验可以较大提升定位的精度。

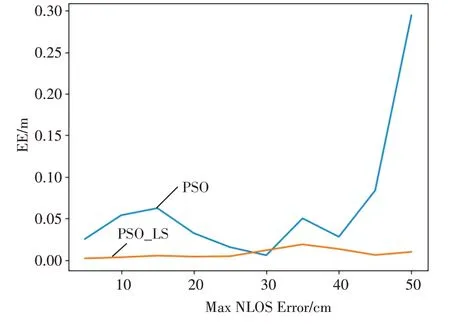
图8 混合环境中AD检验对定位改进

本实验提取满足AD 检验测量数据方法如下。由于NLOS 误差均为正值，考虑偏大的数值均有可能是存在NLOS 的测量数据，通过逐步删除NLOS数据从而达到筛选测量数据的效果。对数据进行整体AD 判断时，若数据不满足近似正态分布假设则删去其较大值并循环上述操作，若近似满足正态分布则输出该组数据。

4 结语

本文将粒子群算法与迭代最小二乘算法相结合，提出PSO-LS算法用于TDOA 室内定位优化，以消除非视距和噪声偏差。主要流程为通过粒子群算法获得定位初值，同时将通过AD 检验的测距结果作为最小二乘的输入，再采用迭代最小二乘算法更新位置估计值。

仿真实验研究了不同初值，步长下的定位精度和收敛速度，对AD 检验在混合环境中应用进行了研究。仿真结果表明，AD 检验能有效地从NLOS和LOS混合环境中筛选出误差较小的项，从数据源上提升定位质量。适当的初始值可以减少计算量，变步长可以在较少的迭代次数下获得较高的定位精度。研究结果可为室内定位提供有意义的参考。