考虑输电线路档距及弧垂影响的故障精准定位
戴 锋,刘贞瑶,陈 轩,康宇斌,郭 嵘,谢 伟
(国网江苏省电力有限公司检修分公司,江苏 南京 210000)
随着电力工业的高速发展和电力系统规模的不断扩大,高压输电线路也日益增多[1-2]。输电线路分布范围较广,沿线地理环境复杂。线路常年暴露在荒郊野外,故障时有发生[3-4]。故障精准定位对于减少故障巡线时间、提升检修运维效率以及保证系统安全稳定运行具有重要意义[5-6]。
输电线路故障测距方法主要分为阻抗法和行波法[7-8]。阻抗法主要利用稳态电压、电流与线路参数、故障距离之间的关系构建故障定位方程,虽然实施成本较低,但易受故障初始条件以及系统参数变动等因素影响而导致测距精度较低[9-10]。行波法利用暂态信号到达时刻、主频率和幅值等信息实现故障精确测距,基本不受故障初始条件影响[11-12],测距精度高,已经在实际高压输电网广泛应用。
根据行波测距原理[13-14],线路长度是影响其测距精度的重要因素之一。高压输电线路长度会受到弧垂、环境温度、负荷电流等因素[15-16]的影响。已有故障测距方法大多直接选取杆塔档距作为计算故障距离时所用到的线路长度。以500 kV线路为例,根据《110~750 kV架空输电线路设计规范》[17],输电线路杆塔大多高30~50 m,导线到达地面的最小距离不超过14 m。若某输电杆塔高40 m,其档距为40 km,然而考虑弧垂影响后,线路导体的实际长度为40.447 km。因此,取档距作为线路长度会对行波故障测距结果造成明显的误差,给检修人员巡线增加了难度。
如图1所示,输电线路杆塔J和K跨河架设。假设实际故障发生在杆塔Q、J间线路的末端F点。如果仅用杆塔档距信息进行行波测距,故障有可能会被定位至杆塔J、K间线路的F′。F、F′不仅是在杆塔两端,也是位于河流两岸。这样的定位误差会误导检修人员选择的路径出现明显错误,增加了故障查找时间,降低了检修效率。

图1 跨河杆塔模型Figure 1 Schematic diagram of a tower acrossing a river
针对上述问题,本文首先利用Haversine公式对输电线路的档距进行修正,然后建立输电线悬链线模型,采用微元法,综合考虑线路导体的受力情况以及对温度对线路导体长度的影响,结合修正后的输电线路档距长度,实现对线路弧垂以及线路实际长度的计算,进而利用双端行波法实现故障精确测距。在PSCAD/EMTDC中搭建500 kV输电线路模型,通过比较线路补偿前、后行波法故障测距误差验证所提方法的有效性。
1 基于Haversine公式杆塔档距修正
关于输电线路档距的测量方法可分为直接法(钢尺测量法)和间接法(碳素钢丝测量法)[18]。
1)直接法。该方法直接人工利用测量工具测量两杆塔之间的档距,该测量方法简单直接有效,但实际操作中因为读数误差及其他因素的影响,这导致测量结果存在些许误差。
2)间接法。该方法将碳素钢丝两端固定在母线横梁中间,并利用紧线器紧缩钢丝来确保得到直线距离,但因为张力等因素的影响,这导致测量精准度不高。
无论利用直接法还是间接法,本质上是人工手动对线路进行测量,测量误差无法难免,因此,需要对实际输电线路的杆塔档距数据进行修正。
针对上述档距测量误差的问题,本文基于电网的地理信息系统所提供的精准杆塔经纬度坐标,利用半正矢公式(Haversine公式)对水平档距进行修正[19],即
(1)
式中θ为地球表面两点与地心的夹角弧度。
假设地球表面任意一点的经纬度坐标为P(δ,φ),δ为经度,φ为纬度,地球半径r≈6 370.856 km。设任意2个杆塔的经纬度坐标分别为T1(φ1,δ1)、T2(φ2,δ2),两杆塔相距Ld,则两杆塔与地球球心的夹角圆心角θT=Ld/r,代入式(1)可得:
hav(2A)+cosφ1cosφ2hav(2B)
(2)
其中,A=(φ2-φ1)/2,B=(δ2-δ1)/2。
由式(2)可求得两杆塔档距距离:
Ld=2rarcsin·
(3)
以某市500 kV电网输电线路杆塔为例,利用式(3)计算档距,档距的测量与计算结果对比如表1所示。

表1 500 kV输电线路杆塔档距测量与计算结果对比Table 1 Comparison of measurement and calculation results of tower spans of 500 kV transmission lines
根据表1,500 kV输电线路杆塔档距测量值之和与实际档距之和相差541.94 m,而经式(3)求得的计算值之和与实际档距之和相差95.23 m,从结果可以看出,计算档距的误差相较于测量档距的误差明显较小。
输电线路档距测量值之和与计算值之和相差634.17 m,约为2~3个档距。若直接利用档距测量值之和作为线路长度,则会导致故障定位结果具有较大的误差。因此,利用本文方法修正输电线路杆塔档距,可以减小因线路长度的测量误差给定位精度带来的影响。
2 基于温度及弧垂补偿的输电线路双端行波测距
假设将架空线看作是没有刚性的柔性锁链,架空线的刚性作用对悬挂空间的曲线形状几乎没有影响,其在架空线上的荷载沿线均匀分布。基于以上假设,悬挂在两杆塔之间的架空线呈悬链线模型[20]。输电线路弧垂计算通常有悬链线和抛物线2种模型[21],考虑到精度问题,本文通过搭建悬链线模型进行电气距离补偿。
建立架空线悬链线模型,如图2所示。模型以弧垂最低点为原点建立坐标系,并设悬挂点为M、N。任取线上一点P进行受力分析,如图3所示,线段OP在导线自重G、水平应力σ、斜应力F2的共同作用下保持平衡。

图2 架空线不等高式悬链线模型Figure 2 Overhead line unequal height catenary model

图3 弧长微元受力示意Figure 3 Force diagram of the OP conductor segment
根据受力分析可得:
(4)
式中 dx为OP的长度;β为水平线和F2之间的角度;ω为自重比载。
根据式(4),可以得到函数表达式:
(5)
当x=0时,y=0,此时可求出C=-σ/ω,即式(5)可变换为
(6)
式(6)即为以弧垂最低点为原点的架空线路数学表达式。根据式(6)即可进一步求得电气距离补偿后的线路实际长度。
图2中设M坐标为(-a,h),N坐标为(l-a,h+H),其中,h表示M到达弧垂最低点的垂直距离,H表示悬挂点M、N之间的高度差,l表示档距长度,此处取修正后的档距长度。
根据H,有
y(l-a)-y(-a)=H
(7)
基于式(6),可求得:
(8)
将经式(3)修正后的档距长度L和式(8)所计算的a代入弧长计算公式,可得线路长度为
(9)
根据式(9)可知,悬挂点M、N点高度差越大,线路档距越大,线路实际长度越大,即其受弧垂影响越大。
在实际运行现场中,导线运行温度受外界环境因素、导线负荷影响。当没有电流流过导线时,其温度和外界环境温度保持一致;当有电流流过导线时,其产生的热量一部分使自身温度升高,一部分散发到周围的环境中,直至达到稳态,导线达到稳定运行状态。受到温度的影响,导线会发生热胀冷缩。其伸缩量为
L1=α(T-T0)L′
(10)
式中a为伸缩系数;T0为基准温度;T为导体当前温度。
因此,综合考虑导线温度影响,导体实际总长度为
L=L′+L1=[1+α(T-T0)]L′=
(11)
中国年平均温度在10 ℃左右,大部分地区常年在40 ℃以下。根据《110~500 kV架空送电线路设计技术规程》[22],输电线路最高允许温度不超过70 ℃,华东地区不超过80 ℃[23]。假设输电线路导线长度仅受温度影响,以LGJ-300/40 mm2型钢芯铝绞线为例,其自重比载为35.06×10-3MPa/m,水平应力为53.955 MPa。将温度为15 ℃时的线路长度作为基准,利用式(11)计算不同温度下的导线长度。
输电线路导线长度随温度和档距的变化关系如图4所示,可知导线长度随温度升高而增大。在相同温度条件下,导线长度越长,其变化就越明显。综上所述,在长距离高压输电网中,线路导线长度更易受温度变化的影响。

图4 不同温度和档距下的线路长度变化量Figure 4 Line length variation at different temperatures and spans
将式(11)所计算的线路实际长度代入双端行波测距公式,可得基于温度及弧垂补偿的双端行波测距结果:
(12)
式中x为故障点至线路首端距离;v为行波波速;t1、t2分别为故障首波头到达线路首、末端的时间。
3 仿真验证
3.1 不同故障位置的影响
在PSCAD中搭建含105个杆塔的500 kV线路,设每一档距长度为390 m,线路总长度为40.950 km。在实际线路长度模型下,每一档距的实际长度为391.076 8 m,线路总长度为41.063 km。为了验证不同故障位置的影响,分别在线路首端、中间、末端设置故障。
在电气距离模型中,假设单相接地故障分别发生在距线路首端2.100、20.430、37.200 km处,线路模型如图5所示。在线路首、末端处采集电压行波信号,采样频率为10 MHz,0.08 s时发生故障,仿真时间为0.15 s。

图5 故障发生在线路首端、中部、末端时的线路模型Figure 5 The line model when the fault occurs at the beginning, middle and end of the line
根据式(12)计算得到定位结果,如表2所示(距005杆塔135.00 m表示故障发生在005、006杆塔之间,且距离005杆塔135.00 m,其他结果同理),电气距离模型下线模行波波头到达线路两端的时间t1、t2如图6所示。根据表2可知,实际距离模型下的定位更为精准,其定位结果的绝对误差相较于电气距离模型下定位结果的绝对误差较小。

表2 2种距离模型下不同故障位置的定位结果Table 2 The positioning results of different fault locations under two distance models

图6 电气距离模型下故障发生在线路首端、中部、末端时线模行波波头到达线路两端时间Figure 6 Traveling wave head arrival time in the line mode when the fault occurs at the beginning,middle and end of the line under the electrical distance model
3.2 不同温度下的影响
以15 ℃为准,在-10、35 ℃的情况下建立电气距离模型。仿真模型和条件与文3.1中相同。如图7所示,假设故障发生在杆塔095、096之间,并且距095杆塔150 m。故障定位结果如表3所示,可知当温度变化时,线路长度也会发生变化,这会对定位精度产生一定的影响,并且在低温下影响更加明显。

图7 故障发生在线路末端时模型Figure 7 The model of the transmission line when faults happen at the end of the line
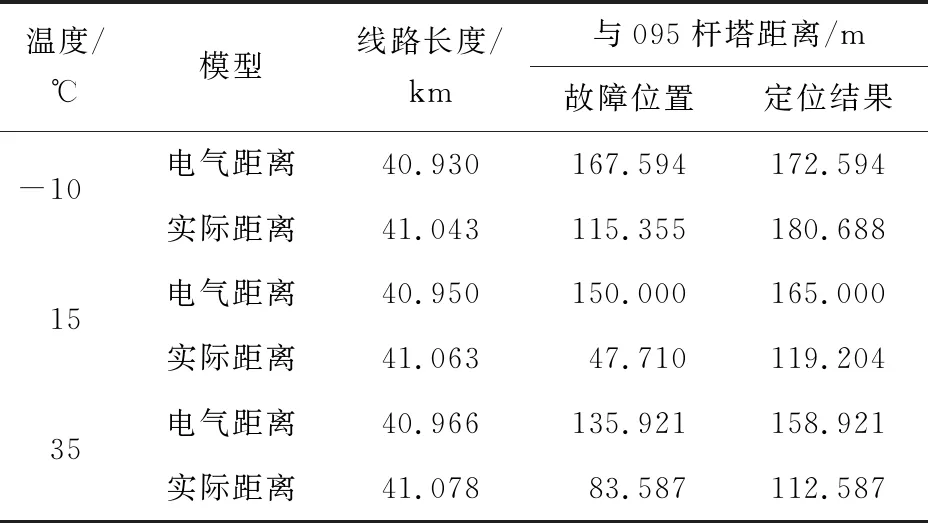
表3 2种距离模型下不同温度的定位结果Table 3 The positioning results for different temperatures under two distance models
4 工程应用
以国内某500 kV输电线路为例,线路总长为27.612 km,沿线共设88个杆塔。具体线路分布如图8所示。

图8 500 kV线路分布Figure 8 The distribution of the 500 kV transmission line
架空线路导体型号为LGJ-630/45,其自重比载为57.033 7×10-3MPa/m,水平应力为86.445 MPa。架空线路y=1.515×103cosh(6.597×10-3x)-1.515×103;不考虑温度影响,线路实际长度L=3.031×103sinh(3.23×10-4l)。
假设单相接地故障发生在距线路首端16.022 km处,即根据电气距离模型(如图9所示),故障发生在杆塔032、033之间,距032杆塔470 m。在线路两端杆塔处采集电压行波信号,采样频率为10 MHz,0.08 s时发生故障,仿真时间为0.15 s。根据线路实际长度模型(如图10所示),故障发生在杆塔032、033之间,距032杆塔403.290 m。
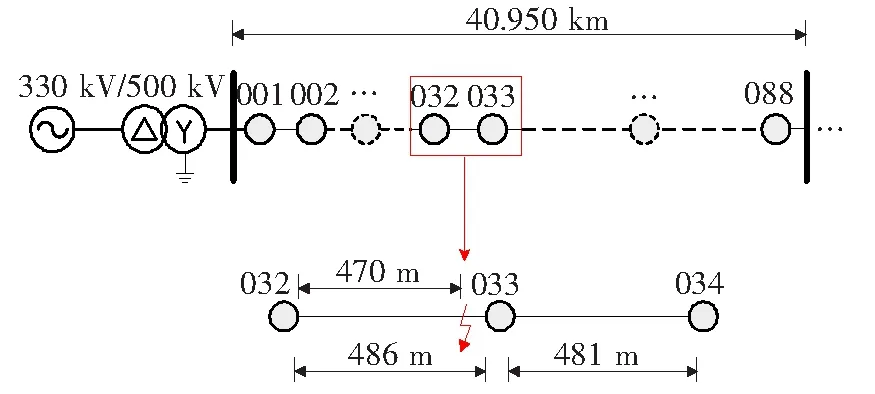
图9 电气距离模型下500 kV线路Figure 9 Schematic diagram of the 500 kV transmission line in terms of electrical distance

图10 实际距离模型下500 kV线路Figure 10 Schematic diagram of the 500 kV transmission line in terms of actual distance
在PSCAD中搭建电气距离模型下的输电线路模型,利用小波变换获取线模行波波头达到线路两端的时间。在电气距离模型下,线模行波波头到达线路两端的时间t1、t2如图11所示。

图11 电气距离模型下线模行波波头到达线路首、末端时间Figure 11 Traveling wave head arrival time in the electrical distance model
根据式(12)计算得到定位结果,如表4所示,可以看出,实际距离模型下故障发生在杆塔032、033之间,但是因为在电气距离模型下的定位误差,将故障错误地定位至杆塔033、034之间。由于杆塔跨河,错位的定位结果会造成检修人员无法快速排除故障。因此,本文所提方法可以有效降低区段定位结果的错误率。

表4 电气、实际距离模型下定位结果比较Table 4 Comparison of fault location results from the electrical and actual distance models
5 结语
本文基于双端行波测距原理,搭建考虑弧垂和温度对输电线路长度的影响的输电线路电气距离补偿模型,根据补偿结果进行故障定位,实现电气和实际距离的映射。
1)通过搭建悬链线模型对线路长度进行修正并进行故障仿真。仿真结果表明,所提方法对发生在线路末端的故障定位效果较为显著。
2)当温度在极高或极低的状况下,本方法对故障位置的修正效果更明显,即对于温度变化较大或极端温度地区弧垂对线路的长度影响更加明显。
3)所提方法可以有效提高故障区段定位的准确率、降低错误率。对于发生在杆塔附近的故障,可以有效降低区段定位误判的可能性。

