高压大排量径向柱塞泵滑靴副流固热耦合数值模拟

李少年，杨攀，包尚令，李毅

(兰州理工大学能源与动力工程学院，甘肃 兰州 730050)

高压大排量径向柱塞泵广泛应用于压机等重载机械领域，泵内3对摩擦副是保证泵正常工作的基本部件，其中定子-滑靴摩擦副(简称为滑靴副)油膜的支承与润滑特性是影响高压大排量径向柱塞泵性能的关键因素.一般认为滑靴的“烧坏”是由于滑靴与定子之间的油膜被破坏而引起配对金属直接接触造成的.因此，保证滑靴副在泵全周期运行过程中始终处于良好的润滑状态至关重要[1].

由于高压大排量径向柱塞泵滑靴副结构特殊，难以使用试验方法对滑靴副特性进行测试，目前对滑靴副动态特性的研究主要采用数值模拟的方法.李新峰[2]对JBP-40型径向柱塞泵滑靴副的油膜特性进行数值模拟，得到不同工况及不同滑靴副结构尺寸下油膜厚度的变化规律.陈俊强[3]建立JBP32H型径向柱塞泵滑靴副流体域流动的数学模型，计算得到不同工况下柱塞泵内压力、速度以及温度场的分布情况.邹姜昆等[4]对高压水介质柱塞泵间隙泄漏问题进行研究，得到工作压力对泄漏量的影响.赵婕等[5]将JBP-40型径向柱塞泵的额定压力提高到35 MPa，对主要运动件进行有限元分析，以验证其强度和刚度.赵勇等[6]对径向柱塞泵滑靴副流场及泄漏量展开研究，分析滑靴副流场的压力与流速的变化.何广进[7]开展径向柱塞泵滑靴的结构设计，并对不同厚度下油膜的密封性和流动状态进行仿真分析.TANG等[8-9]建立考虑摩擦产热的滑靴副全耦合热-力模型，研究了不同工作条件下滑靴结构参数对油膜厚度、压力、温度和泄漏量等性能的影响.

现有径向柱塞泵滑靴副的研究主要集中于低压小排量泵的滑靴副流场特性或结构强度分析，而基于流固热多场耦合的高压大排量泵滑靴副研究鲜见文献报道.同时，现有研究通常将油液视作不可压缩流体，且忽略油液的黏压、黏温特性[10]，这势必造成仿真结果与实际情况有一定误差.文中以某一高压大排量径向柱塞泵滑靴副为研究对象，考虑油液的可压缩性以及黏温、黏压特性对流场的影响，采用热流固耦合仿真的方法，研究不同工况下滑靴副流场与固体域结构强度之间的耦合影响，从而为径向柱塞泵的设计及优化提供一定的参考.

1 数值计算

1.1 计算模型及网格划分

所研究的高压大排量径向柱塞泵设计性能分别为工作压力p=42 MPa，排量Q=1 000 mL/r，转速n0=1 000 r/min；主要几何参数分别为定子半径R=280 mm，转子半径r=215 mm，柱塞直径d=25 mm，偏心距e=23 mm，滑靴旋转圆心距滑靴顶端距离l=44 mm，滑靴宽度a=84 mm，长度b=124 mm，中心油腔半径Ro=20 mm,阻尼孔直径dp=6 mm，滑靴副油膜厚度设定为h=8 μm.泵芯及滑靴副的结构如图1所示.

图1 径向柱塞泵泵芯及滑靴副结构示意图Fig.1 Structure of slipper pair and pump core of radial piston pump

单个滑靴副的流体域及固体域网格划分如图2所示，其中流体域包含滑靴部分和油膜部分.由于油膜部分厚度通常在几微米到几十微米之间，故采用由线到面、由面到体的网格划分策略，以保证在油膜厚度方向至少有5层网格，从而得到质量较高的六面体网格.结构不规则的中心油腔及均压槽部分采用四面体网格进行划分.油膜部分网格与其余部分通过Interface面进行数据交换.固体域网格采用四面体网格进行划分.

图2 计算域网格划分Fig.2 Mesh of computational domain

1.2 网格无关性验证

考虑到油膜的几何特殊性，对油膜部分网格进行加密.设计3种不同网格数N划分方案，以工作压力p=42 MPa时，不同转速工况下油膜出口的泄漏量q为判据指标，进行网格无关性验证，结果如图3所示.可以看出，当网格数约为343.00万时，再增大网格数，泄漏量变化不大.综合考虑计算精度与计算成本，最终选取计算域网格总数为3 430 800，其中油膜部分网格数为1 587 500.

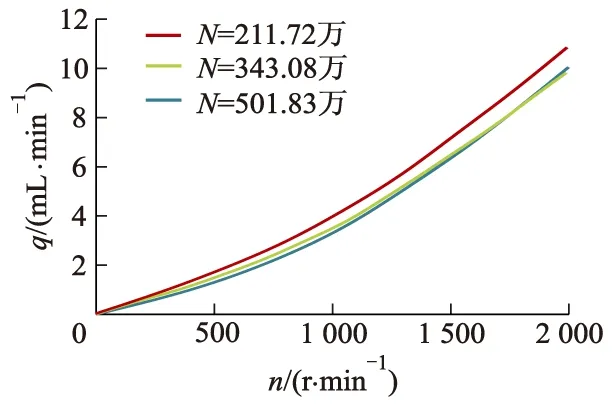
图3 网格无关性验证Fig.3 Verification of mesh independence

1.3 湍流模型与计算方法

应用Fluent软件对径向柱塞泵滑靴副流场进行定常数值计算.工作介质为46号抗磨液压油，该液压油常温常压下密度为870 kg/m3，动力黏度为0.046 Pa·s.采用总压进口边界条件，按照柱塞腔油压变化，总压分别设置为20，30，42 MPa.采用出口压力边界条件，泄漏压力设定为0.2 MPa.设置油液进口温度为常温288 K.油膜外表面转速分别设定为500，1 000，1 500 r/min.

根据流体域实际流态分析，滑靴副流体域整体选用SSTk-ε湍流模型，油膜部分单独设定为层流模型.考虑到油膜流域的几何特性，对油膜流域开启“laminar zone”层流选项.滑靴与定子之间的相对运动通过“moving wall”实现.

应用ANSYS Workbench的静态结构模块和稳态热模块并结合Fluent对滑靴结构进行流固热耦合仿真计算[11].滑靴材料为锡青铜ZQSn10-2-3,其弹性模量为113.4 GPa，泊松比为0.34，导热系数为74.4 W/(m·K)，热膨胀系数为1.83×10-5K-1.对滑靴的定位销孔位置采用固定支撑约束.

由于该部分重点研究在大压差流及强剪切流综合作用下滑靴副油膜流场的压力分布及温升引起的滑靴副结构的应力与变形情况，因此通过单向流固热耦合的方式展开仿真计算.

1.4 流体的弱可压缩性及黏温、黏压特性模型

径向柱塞泵工作压力较高，应考虑油液的可压缩性.相对于具有较大可压缩性的空气，液压油的可压缩性要小很多，称之为弱可压缩性流体.根据流体体积弹性模量的定义进行推导，得到密度随压力变化的表达式为

(1)

式中:E为流体的弹性模量；ρ0为流体初始密度；p为流体受压缩时的压力.

流体的黏温特性体现的是油液黏度受温度的影响，黏压特性体现的是油液黏度受压力的影响.现有的油液黏度与温度、压力的关系式都是经验公式，文中选取Roelands方程[12-13]来表征黏度随温度和压力变化关系，即

(2)

其中

(3)

(4)

式中：μ(p,T)为任意压力p及温度T下油液的黏度；μ0为标准大气压下温度为T0时油液的黏度；λ为Reynolds黏温关系式μ=ae-bT中的黏温系数a；α为Barus黏压关系式μ(p)=μRexp(α,p)中的黏压系数α.

文献[14]提供了不同温度下46号抗磨液压油的黏度测定值，如表1所示.

表1 46号液压油黏温关系试验测定数据Tab.1 Experimental data of viscosity-tempera-ture relationship of No.46 hydraulic oil

将表1数据代入Reynolds黏温关系式计算得到λ值，代入式(4)计算得到S0=1.16.Z0的值参考文献[15]，取Z0=2.3×10-8.最后确定黏度与压力和温度关系式为

(5)

考虑油液的弱可压缩性以及黏温、黏压特性，利用UDF用户自定义函数中的DEFINE_PROPERT预定义宏将压力和温度对油液黏度的影响计入流场仿真计算.

1.5 固体域弹性变形模型

滑靴副固体域材料在油液压力以及温升的双重作用下会产生弹性变形，该弹性变形又会导致油膜形状改变.为了研究因滑靴结构变形而导致的油膜厚度变化，以滑靴底面中心为原点，建立柱坐标系如图4所示，其中垂直面方向为滑靴底面法线方向.点A处流体载荷对点A外任意一点B处所造成的弹性变形量可表示为

图4 固体域弹性变形示意图Fig.4 Schematic diagram of elastic deformation in solid domain

(6)

式中：dδB为点B微元面在滑靴底面法线方向变形量；ν为滑靴材料的泊松比；L为滑靴底面受力点A，B的距离.

2 计算结果及分析

2.1 滑靴副流场数值计算结果及分析

2.1.1 滑靴副流体域的压力分布

图5为在额定工作压力p=42 MPa下，不同转子转速时，径向柱塞泵滑靴副流场的压力分布.可以看出，整体上，不同转速下油膜压力的分布规律基本相同，仅在滑靴中心油腔和两侧腰形区域压力有一定变化.一方面，随着转速的增大，滑靴中心油腔以及密封带部位压力有降低趋势，但下降幅度很小.这是因为定子内表面与滑靴底部配合面之间的相对运动速度增大，使得低压区流体流速增大、流阻减小，从而导致中心油腔压降增大，流体域压力有一定下降.另一方面，中心油腔两侧的腰形区域压力也有变化，左侧(滑靴运动正方向)区域油膜压力继续下降，而右侧(滑靴运动反方向)区域压力继续升高.这同样是因为转子转速增加使得定子内表面与滑靴底部配合面之间的相对运动速度增大，低压区流体流速进一步增大所致.

图5 额定工作压力下不同转速时油膜压力分布Fig.5 Pressure distribution of fluid field under different speeds under rated working pressure

转速的增大，引起滑靴副中心油腔两侧腰型区域内压力变化加剧将导致两侧油膜的厚度及承载能力发生明显变化，严重时会导致滑靴副一侧油膜厚度增大，泄漏量加剧，而另一侧油膜厚度减小，甚至滑靴底面与定子内表面直接金属接触，加剧摩擦磨损以及温升，对滑靴副配合面造成破坏.

图6为在额定转速n=1 000 r/min下，不同工作压力时，径向柱塞泵滑靴副流场的压力分布.可以看出，整体上，不同工作压力下油膜的压力分布规律也基本相同.在转速一定时，随着径向柱塞泵工作压力的升高，滑靴中心油腔的压力也同时升高.

图6 额定转速下不同工作压力时油膜压力分布Fig.6 Pressure distribution of fluid field under different working pressures under rated speed condition

值得注意的是，工作压力变化仅改变了滑靴中心油腔的压力大小，对中心油腔区域之外滑靴副间隙油膜的压力分布影响较小.

2.1.2 滑靴副流体域的速度分布

为了进一步研究滑靴副流体域的流动特征，通过流场仿真得到xoy平面(横向)的油液流速分布情况，如图7所示.

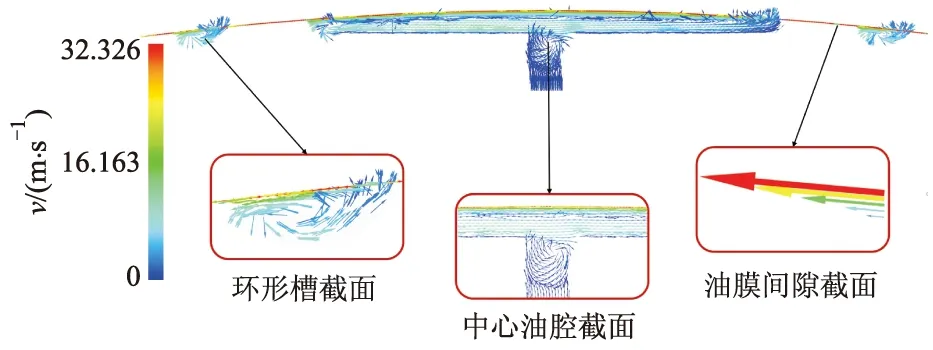
图7 油膜内油液在xoy截面(横向)的速度分布Fig.7 Velocity distribution in xoy section (transverse) of oil film

由图7可以看出：滑靴副流体域不同部位的油液速度分布及流动状态差异较大；油液刚进入阻尼孔时，流速较小，自阻尼孔进入中心油腔后流速有所增大；油液自阻尼孔进入滑靴中心油腔后，由于定子内表面与滑靴的相对运动，使得中心油腔内的油液产生了环形绕流；在滑靴表面环形均压槽内，也有一定的环形绕流；在油膜部分，由于油液黏性摩擦力的影响，在定子与滑靴相对运动的作用下，油膜内油液不再是简单的压差流，而是压差流和剪切流的叠加，因此油膜内油液速度沿着法线方向存在速度梯度.

进一步计算可知，当径向柱塞泵工作压力为42 MPa时，油膜内部油液压力随着转速增大而升高.当转速为1 000 r/min时，随着工作压力的升高，油液流速相差较小，这说明滑靴副油膜油液速度基本不受工作压力影响，主要由泵的转速所决定，剪切流在油膜流动中占主导地位.

2.1.3 滑靴副流体域的温度分布

当工作压力为42 MPa，转速为1 000 r/min时，滑靴副流体域温度分布如图8所示.可以看出：滑靴副流体域内部不同区域温度分布有所不同，滑靴中心油腔和周围环形均压槽部位温度较其他位置明显偏低；在中心油腔两侧，沿着x轴正方向(滑靴的正方向)一侧温度比另一侧温度要低.

图8 滑靴副流体域的温度分布Fig.8 Temperature distribution in fluid field of slipper pair

分析可知，在x轴负方向，油膜在相对运动和黏性摩擦的作用下，受到压差力和剪切力的正叠加作用，故流速高，产热量较大.在x轴正方向，油膜的压差力与剪切力是负叠加，故流动受到抑制，流速低，产热量较小.

温度沿油膜厚度方向逐渐升高，靠近滑靴表面温度最低，而靠近定子内表面温度最高.可见，温度升高主要由于油膜内部油液运动黏性摩擦产热所引起.进一步分析可知，当泵的工作压力增大时，滑靴副流体域各部分温度变化并不明显；当泵的转速增大时，油膜部分的温度有大幅度升高，说明转速对滑靴副油膜的温升影响较大.

2.2 滑靴副流固热耦合数值计算结果及分析

2.2.1 弹性及热变形对滑靴强度的影响比较

在柱塞泵转速为1 000 r/min，油液初始温度为288 K，工作压力为42 MPa的工况下，对滑靴副分别进行流固耦合与热固耦合分析，得到滑靴的变形与应力分布情况，如图9所示.

由图9a,b可以看出，滑靴变形及应力较大的区域位于滑靴底部的中心油腔，这个区域也是阻尼孔的出口位置.该区域需要承受中心油腔高压油液的压力，又是滑靴几何结构比较薄的位置(厚度仅为5.1 mm)，很容易产生应力集中.

由图9c,d可以看出，滑靴的应力与变形区域位置分布与图9a,b基本一致，但是滑靴底面与油膜接触表面的应力明显变大，这是因为滑靴副流体域油膜部分温度较高，故此处滑靴热应力与热变形较大.

图9 分别考虑弹性变形与热变形时的滑靴变形与应力分布Fig.9 Deformation and stress distribution of slipper separately considering elastic deformation and thermal deformation

在上述研究的基础上，进一步对柱塞泵在转速为500，800，1 000，1 200和1 500 r/min时，滑靴分别受到油膜压力场与温度场载荷下的变形以及应力分布情况进行计算，得到滑靴最大变形和最大应力变化曲线，如图10所示.

图10 分别考虑弹性变形与热变形时不同转速下最大变形与最大应力变化Fig.10 Maximum deformation and maximum stress curves of elastic deformation and thermal deformation under different rotation speeds

图10a为在热固及流固耦合情况下，滑靴底面法线方向最大变形量随转速变化的曲线，可以看出：随着泵转速的增大，因油膜温度场导致的变形量呈现持续上升趋势，而压力场导致的变形量却有下降趋势；在同一转速下，流固耦合计算出的变形量总是大于热固耦合计算的变形量，这说明与温度场相比，油膜压力场对滑靴底面的变形影响更大，压力场是主导因素，但两者在数值上相差不大.

图10b为在热固及流固耦合情况下，滑靴底面法线方向最大应力值随转速变化的曲线，可以看出：随着泵转速的增大，因油膜压力场导致的滑靴底面应力值变化较小，而因温度场导致的滑靴底面最大应力值持续增大，这是因为随着泵转速的升高，油膜油液黏性摩擦产热现象进一步加剧，对滑靴结构的影响也进一步增大；在同一转速下，流固耦合计算出的最大应力值总是大于热固耦合计算的应力值，这说明此时油膜压力场仍是主要影响因素.

综上所述，在实际工程应用中，随着径向柱塞泵转速的增大，滑靴副油膜的温升情况会进一步加剧，因此需要采取优化措施以避免因滑靴副温度过高而造成润滑失效，对柱塞泵的滑靴及定子结构造成破坏.

2.2.2 转速对滑靴结构强度的影响

图11为径向柱塞泵在工作压力为42 MPa，初始油温为288 K，泵转速为500，1 000和1 500 r/min时，通过流固热耦合计算得到的滑靴变形与应力分布情况.

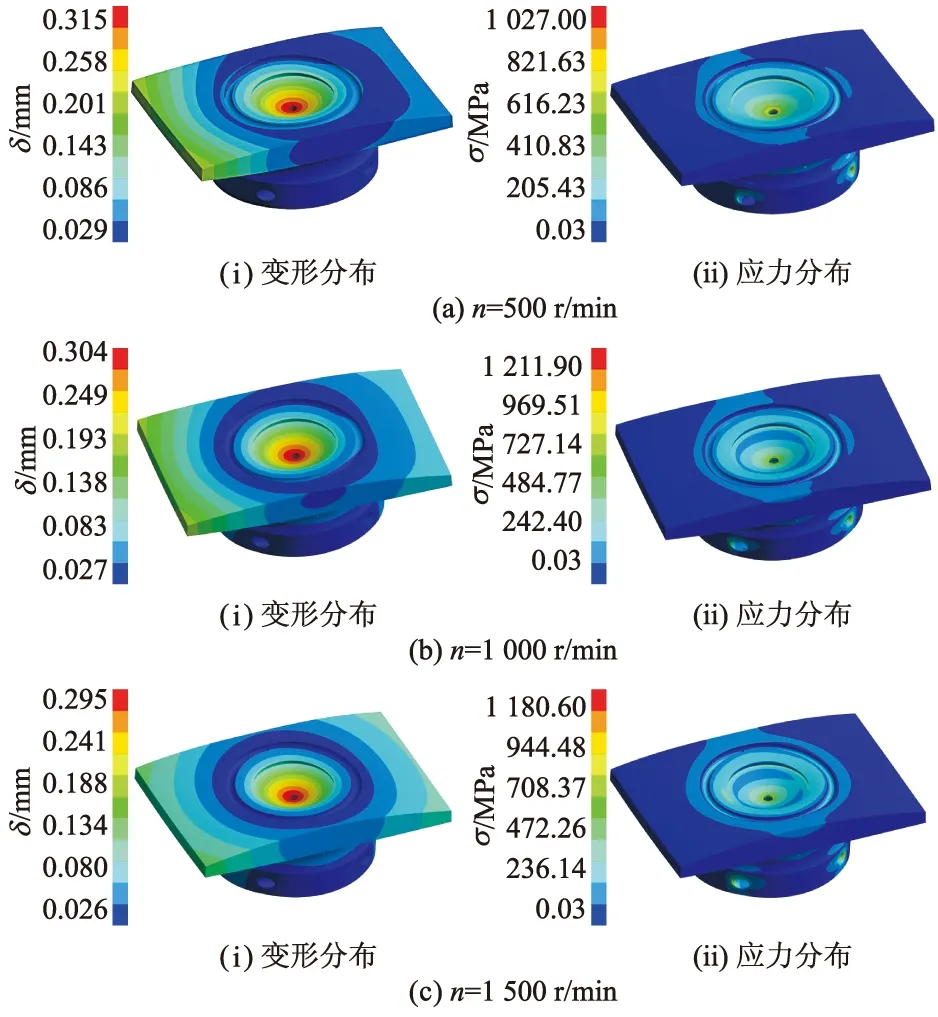
图11 不同转速下滑靴的变形与应力分布Fig.11 Deformation and stress distribution of slipper at different rotation speeds

由图11可以看出：随着泵转速的增大，滑靴的变形与应力分布基本一致，但变化趋势有所不同；滑靴在密封带以及均压槽外侧高应力区域面积有所增加，但是滑靴边缘处变形量却有所减小；滑靴底面最大变形区域与最大应力部位并不在同一位置，这是因为结构的变形不仅与所受载荷有关，还与结构的几何形状密切相关；随着转速增大，滑靴副流体域的压力与温度均有所上升，导致滑靴所受压力与热应力均有所增大，但转速的增大也使滑靴底面与定子之间流体流速增大，故而滑靴底面边缘处实际流体压力有所减小，变形量减小.

在上述研究的基础上，对柱塞泵分别在转速500，800，1 000，1 200和1 500 r/min下滑靴副流体域及固体域进行流固热耦合仿真，得到滑靴底面法线方向最大变形与最大应力变化曲线，如图12所示.

图12 滑靴底面最大变形处变形量与应力值随转速变化的曲线Fig.12 Variation curves of deformation and stress at the maximum deformation of slipper surface with rotational speed

由图12可以看出，随着泵转速的增大，应力出现持续上升趋势，变形则有所下降.

2.2.3 工作压力对滑靴结构强度的影响

图13为柱塞泵转速为1 000 r/min，初始油温为288 K，泵工作压力为20，30和42 MPa时，通过流固热耦合计算得到的滑靴变形与应力分布情况.

由图13可以看出，随着泵工作压力的升高，滑靴的应力与变形分布基本一致，且应力与变形值都有所增大.这是因为随着工作压力升高，滑靴副流体域的压力场变化较大.

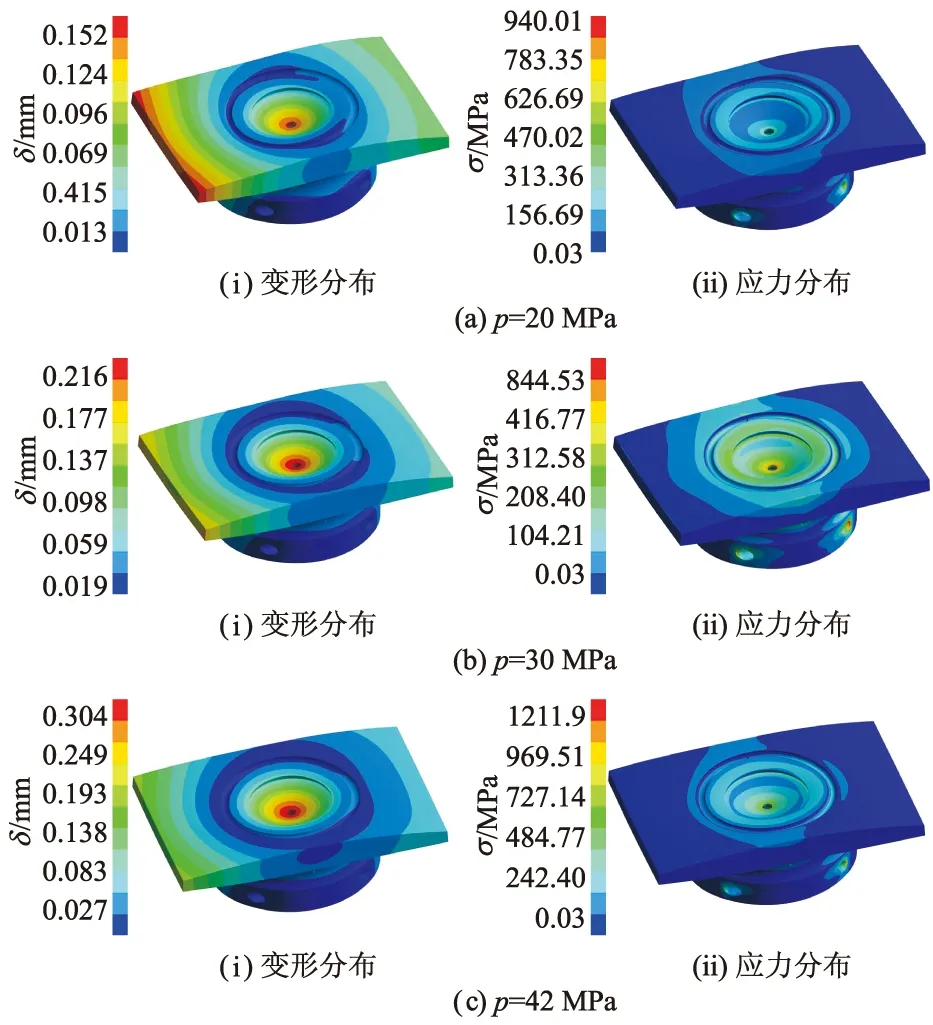
图13 不同工作压力下滑靴的变形与应力分布Fig.13 Deformation and stress distribution of slipper under different working pressures

在上述研究的基础上，进一步对柱塞泵在工作压力10，20，30，35，42 MPa工况下滑靴副流体域及固体域进行流固热耦合计算，得到滑靴底面最大变形与最大应力变化曲线，如图14所示.

由图14可以看出，随着工作压力的增大，变形与应力有所波动，但总体仍呈上升趋势，且变化幅度较大.

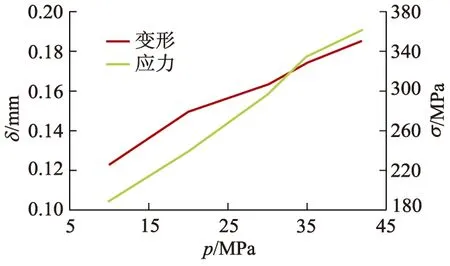
图14 滑靴底面最大变形量与应力值随工作压力变化的曲线Fig.14 Variation curves of the maximum deformation and stress at slipper surface with change of working pressures

3 结 论

在充分考虑油液的弱可压缩性以及黏温、黏压特性基础上，对滑靴副流场及固体域结构展开流固热耦合数值计算，得到如下结论：

1) 随着泵工作压力的升高，滑靴副流体域压力上升.随着泵转速的增大，中心油腔两侧外密封带的压力变化较大，滑靴运动正方向外密封带区域油膜压力下降，而滑靴运动反方向外密封带区域压力升高.

2) 滑靴副流体域的油膜温度变化剧烈，主要由油液黏性摩擦产热引起.温度场的分布基本不受工作压力的影响，而随着泵转速的升高，油膜温度明显增高.可见，在剪切流作用下，油液的黏性摩擦力是柱塞泵滑靴副温升的主要因素，同时也是柱塞泵能量损失以及效率降低不可忽略的原因.

3) 滑靴的最大变形与应力均出现在中心油腔底部阻尼孔出口边缘处.该位置几何结构较薄，且承受中心油腔高压油压力载荷与温度载荷，因此是整个滑靴结构强度较为薄弱的部分.

4) 滑靴副流体域温度场对滑靴底面变形的影响要小于压力场，但总体处在一个数量级上.同时，随着泵转速的升高，油膜温升逐渐增大，使得温度场对滑靴变形的影响不断增大.