不同亚格子模型在水翼云空化数值计算中的适用性分析
洪锋,薛环铖,张帆,胡涛*
(1. 三峡大学水电机械设备设计与维护湖北省重点试验室,湖北 宜昌 443002;2. 三峡大学机械与动力学院,湖北 宜昌 443002;3.江苏大学国家水泵及系统工程技术研究中心,江苏 镇江 212013)
空化是一种复杂两相湍流流动,包含了空泡的产生、生长、收缩和溃灭等多种非稳态过程,涉及可压缩、旋涡运动和多尺度流动分离等非定常特征.空化在流体机械中广泛存在,严重时会造成机组振动、噪声及空蚀等问题[1-2].
由于空化具有高湍流特性,湍流模型在准确模拟空化流中起着重要作用[3].大涡模拟(LES)已被证明能够精确再现流场的不稳定性[4],并在水翼云空化流动问题中得到了广泛应用[5-6].为研究二维几何条件下LES模型的适用性,ROOHI等[7]和谢庆墨等[8]分别在OpenFOAM和Fluent平台,实现了对二维Clark-Y水翼云空化的精确计算,验证了2D LES方法模拟翼型空化的可行性.
LES引入了一种基于空间平均的滤波方法,对大尺度流场直接求解,并通过亚格子模型对较小的涡流进行模化处理.Smagorinsky- Lilly涡黏性模型为最早的亚格子模型,该模型中的系数Cs是一个经验值,导致该模型在计算过程中常产生过度的耗散[9].随着研究的深入,相继产生了动态亚格子模型(KET),以及考虑湍流壁面效应的亚格子模型,如WALE模型.不同亚格子模型主要聚焦于单相、简单流动的研究,如后向台阶流动问题[10].然而,空化流场的剧烈非定常特征,导致了流动结构的复杂性和多变性,在LES中所选取的亚格子模型需充分捕获大小尺度湍流结构之间的相互关系,并最终决定了空化流动数值计算的精确度.但目前水翼空化流场数值计算较少关注大涡模拟方法中亚格子模型的适用性问题.
为了分析不同亚格子模型在空化非定常流动中的计算精度及适用性,文中分别使用4种亚格子模型,对二维Clark-Y水翼周围云空化流动特性进行模拟,并与相应试验结果对比研究,从而对上述亚格子模型计算效果以及精确性进行评价.
1 数值模型
文中采用Mixture多相流模型,假设多组分具有相同的分速度.空化模型采用Zwart模型,该模型基于Rayleigh-Plesset方程,并假设系统中气泡具有相同的尺度.Zwart模型在水翼、离心泵等流体机械空化流动数值计算中得到了广泛应用[11-12].
LES对Navier-Stokes方程进行滤波,并将湍流分解为可解大尺度和不可解小尺度2个部分.滤波后的Navier-Stokes方程[13]为
(1)
式中:τij为亚格子应力;Sij为应变率张量.
Smagorinsky-Lilly亚格子模型湍流黏度系数[14]计算式为
(2)
式中:Ls为亚格子尺度的混合长度;D为翼型表面第一层网格厚度;k为Karman常数;Cs为Smagorinsky常数,取0.1;Δ为局部网格尺寸.
在WALE亚格子模型中,湍流黏度系数[15]为
(3)
(4)
其中Cs取0.325.
WMLES模型会在空间和时间尺度都过小的近壁区域激活RANS模式,在网格大小足以解析自由流的局部大尺寸时切换到大涡模拟LES,其湍流黏度系数[15]为
(5)
式中:dw为距壁面的距离;S为应变率;取κ= 0.41,Cs= 0.2;hmax为最大网格尺寸;hwn为标准网格间距;取Cw=0.15.
KET亚格子模型增加了对亚格子尺度湍流效应的模拟,其湍流黏度系数[16]定义为
(6)
式中:ksgs为亚格子动能;参数Ck的值根据流场状态调整.
2 计算域及网格划分
2.1 数值计算模型
研究对象为弦长C=70 mm、翼型攻角α=8°的Clark-Y型水翼.水翼位于矩形流场中,流场域的几何参数如图1所示.计算域边界条件设定与ROOHI等[7]的研究保持一致,即流场入口设置为速度入口边界,速度Uin=10 m/s;出口设置为压力出口边界,压力值由空化数决定;上壁面和下壁面以及水翼表面均设为无滑移壁面条件.

图1 计算域Fig.1 Computational domain
2.2 网格无关性分析
采用WALE亚格子模型计算水翼非定常流动,来验证网格无关性.验证的网格数分别为80 636(Mesh1),127 696(Mesh2),170 066(Mesh3)及253 764(Mesh4).翼型壁面周围采用O型网格,并对近壁面网格进行加密.文中采用压力-速度直接耦合法(couple)求解控制方程,扩散项采用二阶中心差分格式,对流项采用高阶分辨率格式.瞬态项采用非稳态二阶隐式时间积分格式.为满足湍流模型对壁面网格的要求,y+的值不大于1.根据Courant-Friedrichs-Lewy condition条件,确定时间步长Δt= 1.0×10-6s.
表1为σ=0.8条件下,采用4种不同网格计算得到的平均升、阻力系数Cl,Cd.从表中可以发现,Mesh2计算所得的升阻力系数与试验值已较为吻合,且继续增大网格数量,升阻力系数的变化基本稳定,表明网格数量没有导致求解误差.因此,选择Mesh2作为文中的计算网格.
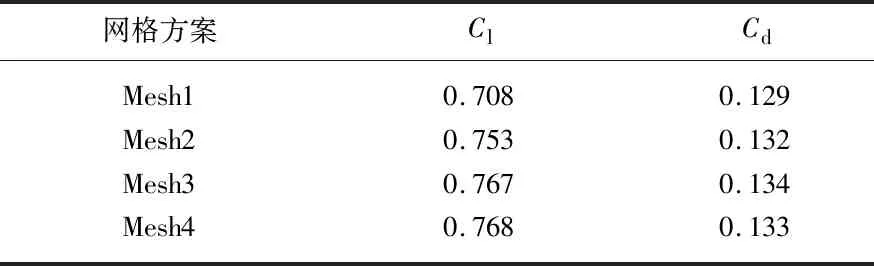
表1 不同网格数下的升、阻力系数对比Tab.1 Comparison of predicted lift and drag coe-fficients based on different grids
3 结果与讨论
3.1 升阻力系数变化规律
图2为4种亚格子模型在一个空化周期内升力系数的瞬时变化,并与试验值进行对比.

图2 不同亚格子模型预测的瞬时升力系数与试验值的比较Fig.2 Comparison of transient lift coefficient obser-ved by different sub-grid scale models and experiments in cavitation cycle
由于空泡生长、脱落和溃灭,升力随时间呈现振荡变化.空泡长度达到最大时升力系数最大,而小幅度的振荡说明云空化阶段空泡的小规模分离.对比发现,WALE模型预测的瞬时升力系数周期性变化更接近试验数据,KET模型及WMLES模型预测的升力系数峰值较高,升力系数变化过程较为剧烈,Smagorinsky-Lilly模型预测的升力峰值虽然与试验较为接近,但周期性变化明显弱于WALE模型的预测结果.
表2为不同亚格子模型模拟得到的平均升、阻力系数与相应试验值的对比.从表中可以看到,文中采用的WALE模型模拟得到的平均升力系数与试验值的相对误差δ在1.00%以内,而其余3种模型的计算值及文献预测值均大于1.00%;就平均阻力系数而言,文中WALE与Smagorinsky-Lilly模型预测的结果与试验值的相对误差均在12.00%以内,且远远低于ROOHI等[7]的预测值.综上,根据平均升阻力系数及瞬时升力系数预测精度,文中采用的WALE具有较好的适用性与可行性.
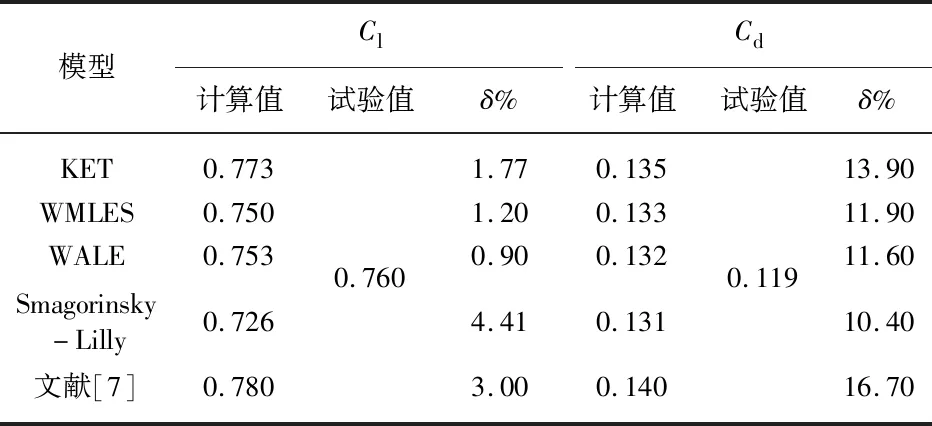
表2 4种亚格子模型计算得到的平均升力、阻力系数对比Tab.2 Comparison of average lift and drag coefficients calculated by four sub-grid scale models
3.2 时均速度分布规律
图3为σ=0.8时,沿水翼吸力面垂直方向5个不同位置(x/c=0.2,0.4,0.6,0.8,1.0),不同亚格子模型预测的平均速度分量与相应试验值[13]的对比.

图3 时均速度数值结果与试验数据的比较Fig.3 Comparison of numerical results of time-averaged velocity with experimental data
从图3中可以看到,当x/c小于等于0.4时,水翼前缘处速度平均值大于0,而当x/c大于等于0.6时,水翼后缘处由于逆压差的影响,速度出现负值,表明产生了回射流.对比发现,4种亚格子模型预测的平均速度与试验结果均吻合良好.在空化和非空化区域以及边界层内部,不同亚格子模型预测的结果差异也较小,这是由于4种亚格子模型在壁面及主流区域预测到的空化程度比较接近.
3.3 云状空泡周期性演变
图4为不同亚格子模型模拟得到的空泡形态周期性变化和试验结果对比.观察发现,不同亚格子模型计算得到的空泡演变基本符合试验结果.在5%T至20%T,上一个空化周期的云空泡团脱离翼型表面,向下游低压区移动并完全溃灭,此时附着型空泡在前缘产生并向后缘生长,空穴的厚度和长度随之变大.随着时间推移,空泡几乎完全覆盖整个翼型表面.

图4 不同亚格子模型模拟得到的空泡形态的周期性变化和试验值的比较Fig.4 Comparison of periodic changes of cavity shape simulated by different sub-grid scale models and experimental data
在60%T至70%T,空穴从尾缘开始破裂并向前缘推进,回射流进一步向上游移动,导致空穴断裂;在81%T至97%T,前缘的附着型空泡基本溃灭,尾缘处形成大尺度空泡团.随时间推移,前缘开始产生较薄的附着型空泡,尾缘大体积空泡团脱落并向下游运动.
比较4个模型模拟结果可以发现,WALE模型模拟得到的空泡体积分数云图与试验结果更接近.具体体现在:① 根据试验描述,在10%T时刻,翼型尾缘处大体积云空泡团还在翼型表面,WALE模型的结果与试验相符,其他3个模型的云空泡团已脱离尾翼表面;② 在20%T时刻,试验结果中,翼型表面上的片状空泡长度与厚度达到最大,几乎覆盖整个吸力侧表面,WALE模型较好地满足这一特性,而KET及WMLES模型所预测片状空泡厚度及长度都过低;③ 根据文献[13] Clark-Y水翼试验结果得出,云空化的不稳定性主要归结于回射流的作用.在60%T时刻,回射流开始作用于尾缘处并向前缘推进,空腔闭合处的反向压力梯度有利于回射流的发展.KET与WMLES模型其后缘处有小规模空泡断裂,其回射流作用效果过大,相较之下,Smagorinsky-Lilly与WALE模型更符合试验结果;④ 片状空化在翼型中部断裂,其空泡长度减少至上一时刻的2/3左右,WALE模型的结果与试验数据较吻合,尤其是翼型中后部空穴特性.此外,图5为20%T时刻,水翼尾缘处的速度矢量分布图,对比发现WALE模型尾缘处空泡受到的回射流影响很小,逆压力梯度作用不明显,而Smagorinsky-Lilly模型此时受到回射流影响,片状空穴尾端发生明显回缩,回流长度增大,表明除WALE模型以外的亚格子模型过早地预测到翼型尾缘的回射流结构.因此,总体上,WALE模型能较好地预测云状空化周期性演变过程及其流动细节.

图5 20%T时水翼尾部速度矢量分布图Fig.5 Velocity vector distribution diagram of hydro-foil tail at 20%T
为进一步理解空化流动机理,研究空化与旋涡相互作用.利用Q准则对非定常涡结构进行可视化,Q准则定义为
(7)
式中:ω为旋转率张量;s为应变率张量;Q准则表明旋转与变形之差,其值表示旋转强度的大小,用正值来识别涡流,负值则说明在该区域作为主导的为剪切作用.
图6为利用WALE模型预测的一个空化发展内某一时刻Q值分布情况.观察得到,5%T时刻,大尺度云状空泡团运动到水翼尾缘,尾缘附近Q值分布较大,表明此处存在较强的旋转和剪切作用;20%T时刻,片状附着性空穴向后缘生长,在空穴内部的Q值较为稳定,表明在空穴内部流体的旋转效应和剪切效应相对平衡,没有表现出明显的涡流;70%T时刻,在回射流的作用下,片状空穴发生断裂,且断裂空泡周围Q值为负,说明回射流的轴向变形效应较强;90%T时刻大尺度空泡团生成,空泡团边界及尾缘附近的Q值为正且绝对值极大,说明这部分区域有较强的旋涡作用,旋转与剪切效应相互制衡和转化,致使该区域流动出现不稳定.

图6 WALE模型计算得到的Q值分布Fig.6 Q value distribution calculated by WALE model
4 结 论
1) 与其他3种亚格子模型相比,WALE模型预测的平均升阻力系数与试验结果最为符合,且在1个典型空化周期内,WALE模型预测的瞬时升力变化趋势与试验也最接近.
2) 4种亚格子模型预测的空泡演变过程基本与试验相符,但WALE模型模拟得到的空泡在云空化周期内的形态、大小与位置更符合试验结果,能够比较准确地捕捉到二维Clark-Y水翼云空化时翼型尾部回射流作用所导致的空泡断裂效果,并精确预测到大型空泡团的脱落及其体积变化特征.
3) 使用Q准则,描述了基于WALE模型下翼型空化流动中的旋涡结构,得到了片状空化脱落所产生的强烈旋转与剪切作用对流场不稳定性的影响.

