空间机械臂在轨插拔孔操作的超扭曲滑模阻抗控制

曾晨东，艾海平，陈 力

（1. 江西理工大学 能源与机械工程学院，南昌 330013；2. 福州大学 机械工程及自动化学院，福州 350108）

空间站作为长时间运行的载人航天器，其站内的插拔、旋拧、搬运等复杂精密的太空操作任务多依赖宇航员出舱执行[1-3]。宇航员出舱执行此类太空任务时，由于操作空间有限、操作时间较长、精度要求较高，存在成本高、效率低、风险大等问题。为此，用空间机械臂代替宇航员完成此类太空任务具有重要意义[4,5]。

目前，世界各航天大国有近20座空间机械臂正在或计划应用于执行复杂精密的在轨操作任务。针对空间机械臂执行太空操作任务方面的研究，Yoshida等[6]基于动量守恒定律研究了空间机械臂捕获卫星的碰撞动力学及运动学问题。陈德相等[7]针对航天器自主任务规划中的资源受限、约束复杂、活动并行等问题，提出了基于时间拓扑排序的航天器资源计算方法。Huang等[8]针对空间机械臂捕获卫星后质量特性与反作用轮结构发生变化的问题，提出了一种改进的状态依赖Riccati方程最优控制器。Gasbarri等[9]介绍了空间机械臂捕获卫星前后的两种控制策略，实现了对柔性构件的柔性激励补偿。Gangapersaud等[10]分析了空间机械臂抓捕非合作、翻滚目标时末端执行器的力/力矩。龚柏春等[11]分析了空间非合作目标近程交会过程，并提出了基于相机偏心安装“杆臂效应”提供状态可观测性的仅测角相对导航算法。

上述研究成果多局限于空间机械臂的捕获、对接、交会等，其模型及工况不适用于空间机械臂在轨部件替换及在轨燃料加注。另外，对于长期运行的空间站，其站内的插拔、旋拧、搬运等任务属于复杂精密的操作，而目前对空间机械臂相关操作的精度控制问题鲜有研究。考虑空间机械臂在轨部件替换、在轨燃料加注及空间站站内任务过程包含插拔孔操作，而上述研究均未涉及。综合分析以上内容，本文提出对空间机械臂在轨插拔孔操作的相关问题进行研究。

值得一提的是，空间机械臂系统由于存在非完整动力学约束，系统会产生强烈的动力学耦合作用，相关在轨操作控制过程较为复杂。针对空间机械臂在轨操作的研究，Nanos等[13]提出了一种柔性关节空间机械臂末端跟踪的反馈线性化控制策略。付晓东等[14]设计了一种全柔性空间机械臂运动振动一体化输入受限重复学习控制策略。Wang等[15]研究了空间机械臂捕获非合作卫星后组合体系统的解耦策略及协调控制方案，提出了基于四次Bézier曲线和特定约束条件下的自适应粒子群优化算法。Luo等[16]考虑了混合体系统的不可测状态、未知惯性特性和外部干扰，提出了一种基于有限时间收敛的鲁棒无惯性预定性能控制策略。

上述控制策略虽可对空间机械臂有效控制，但存在结构较复杂、计算量较大等特点，不适用于空间机械臂在轨插拔孔操作。滑模控制作为非线性控制，其算法简单，具有快速全局收敛特性，对外部干扰和参数摄动具有鲁棒性。然而，由于滑模控制含有不连续的切换控制律，导致执行器跟踪速率过快，引发抖振现象。抖振不仅会降低系统的鲁棒性和稳定精度，甚至可能激发未建模动态，破坏系统的稳定性。考虑到超扭曲算法不仅具备普通滑模控制的优点，而且能将滑模变量及其一阶导数在有限时间内收敛到零，同时有效地抑制抖振现象[17]。基于此，本文提出超扭曲滑模阻抗控制策略。

考虑太空环境中，空间机械臂系统的燃料异常宝贵，若对其载体位置、姿态进行控制，将大幅增加操作成本，故本文建立载体位置、姿态均不受控的空间机械臂系统动力学方程；利用系统位置几何关系，建立了部件插头在基联坐标系下的运动雅可比关系；结合阻抗控制原理，建立了阻抗控制模型。然后，提出了超扭曲滑模阻抗控制策略，控制策略分为位姿跟踪控制内环和阻抗控制外环。最后，为保证插孔操作过程的精确控制，采用分段控制方案将插孔操作细分为两个阶段。将上述控制策略应用于空间机械臂在轨插拔孔操作，并对操作过程进行仿真，分析校验所提控制策略的有效性。

1 运动学、动力学及阻抗模型分析建立

1.1 运动学、动力学模型分析建立

空间机械臂在轨插拔孔操作模型如图1所示，其由自由漂浮的载体 B0，机械臂杆 B1、 B2、 B3及部件BP组成。OC0、 OCi（ i= 1,2,3）、OCP分别为载体、机械臂杆、部件的质心； O0、 Oi（ i= 1,2,3）分别为载体、关节铰几何中心，其中 O0与OC0重合；x0为 O0到 O1的连线， xi（ i= 1,2,3）为机械臂杆 Bi的对称轴；XOY、x0O0y0、 xiOiyi（ i= 1,2,3）分别为系统惯性坐标系、载体质心坐标系、关节铰中心坐标系；X'O1Y'为系统基联坐标系，X'方向与载体水平面平行，Y'方向与载体竖直平面平行。

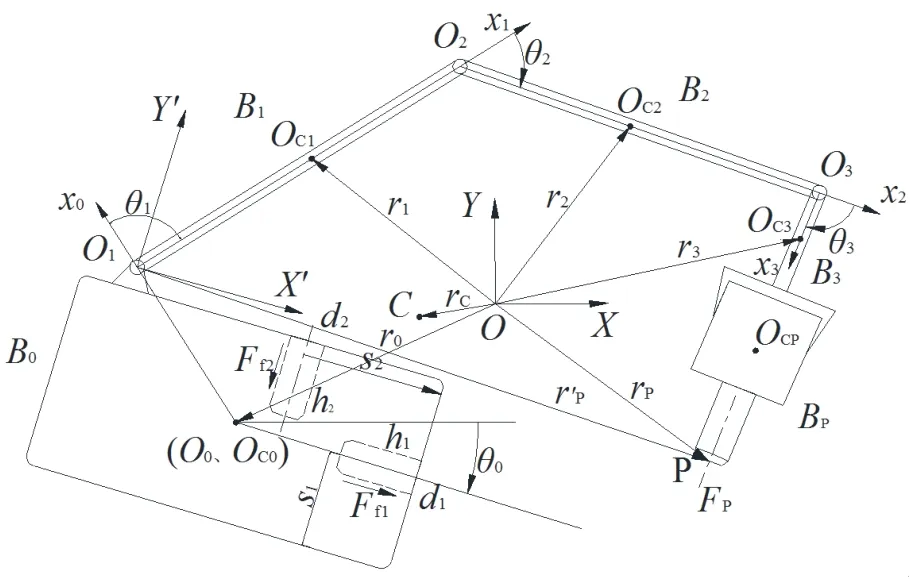
图1 空间机械臂在轨插拔孔操作模型Fig.1 Model of space manipulator orbit insertion and extraction operation

定义载体质量、转动惯量和质心 O0到 O1的距离分别为 m0、I0、 L0；各臂杆质量、转动惯量、长度分别为 mi、Ii、 Li（ i= 1,2,3）；部件 BP的质量、转动惯量、长度分别为 mP、IP、 LP；关节铰中心 Oi到臂杆i质心的距离为 di（ i= 1,2,3）；载体姿态角、关节转角、部件插头转角分别为θ0、 θi（ i= 1,2,3）、θP；系统总质量为M，总质心为C，矢径为rC；载体质心矢径为r0；各臂杆质心矢径为 ri（ i= 1,2,3）；部件插头末端P点在惯性坐标系下的矢径为rP，在基联坐标系下的矢径为；h1为侧面孔深度，h2为正面孔深度；S1为侧面孔轴线到载体底部的距离，S2为正面孔轴线到载体右侧的距离；FP为部件插头输出力及力矩，Ff1、Ff2为插拔孔操作过程中孔内摩擦阻力及力矩。

忽略太空的微重力影响，载体位置、姿态均不受控的空间机械臂系统为无外力作用的自由漂浮无根多体系统，其遵循对XOY的动量守恒，及对O点的动量矩守恒，不失一般性，假设系统初始动量、动量矩均为零。根据第二类拉格朗日方程，可得到欠驱动形式的空间机械臂系统动力学模型：

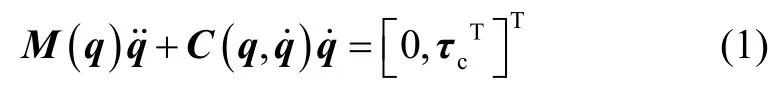
式中，q = ［θ0,θ1,θ2,θ3］T为系统广义坐标；M （q ） ∈R4×4为系统对称、正定的惯性矩阵；C (q,∈R4×1为包含科氏力、离心力列向量； τc∈R3×1为关节电机输出力矩。

对式(1)进行如下分块：

考虑到空间机械臂在轨插拔孔操作中，载体位置、姿态均不受控，因此需要研究部件插头在基联坐标系内的轨迹运动情况。为建立部件插头末端P点相对于载体 B0的位姿关系，将部件插头末端P点相对于 O1的矢径向基联坐标系X'O1Y'内投影，并定义L3P=L3+LP，得到：

又可知，在基联坐标系X'1OY'内，臂杆3与部件插头姿态保持一致，故有结合式(3)对时间t求导，得到部件插头末端P点相对运动Jacobian关系：

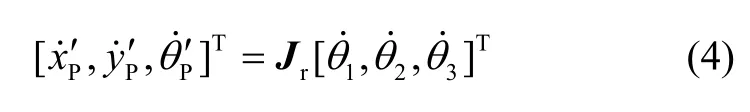
式中， Jr∈R3×3为相对运动Jacobian矩阵。

1.2 阻抗模型建立

阻抗控制作为机械臂控制中非常有效的一种控制方法，其目标是通过调整机械臂阻抗参数来保持末端的位姿、末端与环境之间接触力的理想动态关系，即通过阻抗关系模型将力和位姿容纳到同一框架，对力和位姿的动态关系进行调整。

考虑到空间机械臂在轨插、拔孔操作对部件插头输出力和位姿的要求，将阻抗控制应用于空间机械臂在轨插拔孔操作不失为一种有益尝试。一般的，部件插头阻抗关系的数学模型可表现为二阶微分方程形式，环境模型可近似为二阶非线性函数形式：

根据式(5)可计算出部件插头输出力及力矩 Fp与部件插头接触力及力矩 Fe的误差，得到表达式：

结合上述内容，并定义 rA为θq变换到X的过程，则可得到如图2所示的阻抗控制流程。

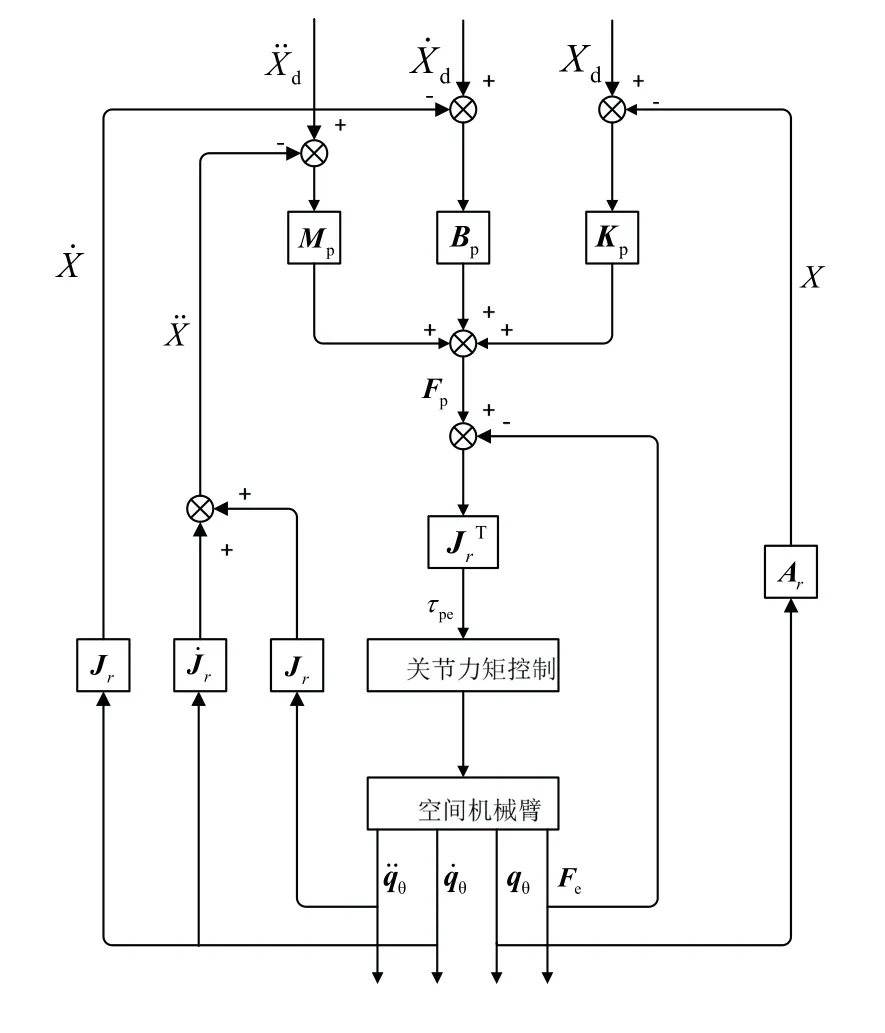
图2 阻抗控制流程Fig.2 Impedance control process

由此，在空间机械臂在轨插拔孔操作过程中，若开启阻抗控制，则式(1)表示的载体位置、姿态均不受控的空间机械臂系统动力学模型可写为：

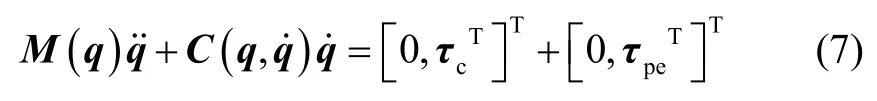
2 超扭曲滑模阻抗控制策略设计

2.1 超扭曲算法

超扭曲算法与普通滑模控制算法相比，其可将高频切换部分隐藏至滑模变量的高阶导数中，因此可有效地抑制普通滑模算法产生的抖振。此外，超扭曲算法考虑了系统动力学不确定与外部扰动的影响，能在有限时间内使滑模变量及其一阶导数收敛至零。

引理 1 考虑如下受控系统：

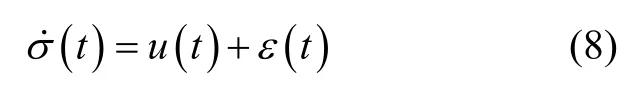
式中， σ （ t ）∈ R为状态量； u（t）表示系统控制输入；ε（ t ）表示有界的外部扰动，并且满足C表示外部扰动导数的上界。

根据式(8)，结合超扭曲算法，得到扰动条件下的非线性方程：

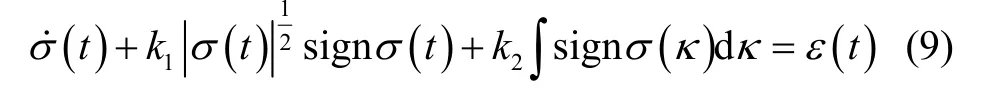
式中，1k和k2均为常系数。

2.2 超扭曲滑模控制内环设计

空间机械臂在轨插拔孔操作过程中，存在动力学不确定及外部扰动，故式(7)可写为：

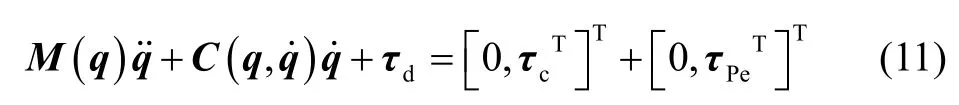
式中， KP∈R3×3表示系统动力学不确定及外部扰动项。

考虑到空间机械臂系统动力学方程是欠驱动、不完全能控的，这将不利于控制系统的设计。在此，采用增广变量的方法，即虚拟扩展系统的控制输入及输出，以解决这一问题。为此，对系统输出的X加以扩展，定义则可导出新的运动雅可比关系：

由于研究的是部件插头运动轨迹，联立式(11)(12)，可得：

式中，

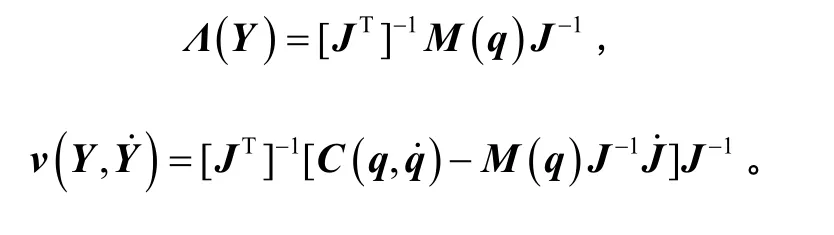
同时，为利于控制器的设计，将式(13)写成式(14)所示状态向量形式：

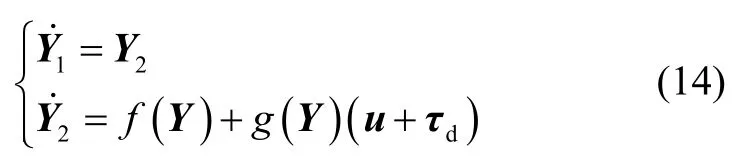
基于式(14)，设计如下滑模变量：

式(15)求导后可得：

结合式(14)(16)可得：

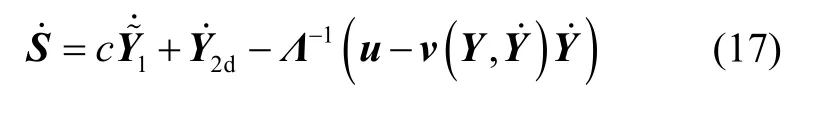
为此，设计如下系统控制输入：

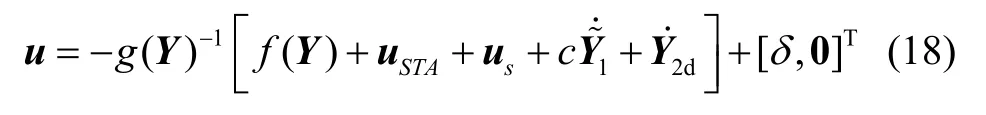
式中，us、uSTA分别为滑模控制项、超扭算法控制项。

超扭算法控制项的定义如下：

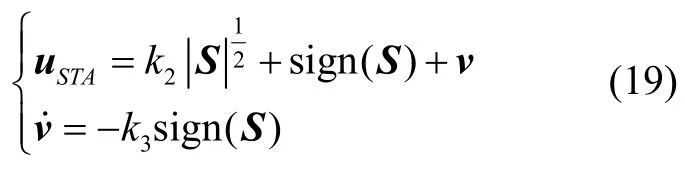
式中，k2、k3＞0。

滑模控制项的定义如下：

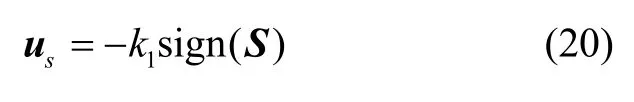
式中，k1＞0。

结合式(17)-(20)，可得到以下闭环系统：

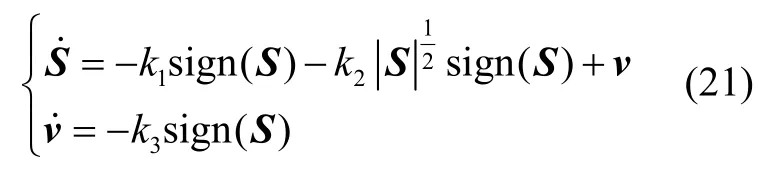
定理 1结合式(18)(21)，对于存在动力学不确定及外部扰动的系统，其轨迹跟踪误差可以收敛到零，即系统满足渐近稳定性。

证明根据式(21)，可定义χ，其表达式如下：

由此，可定义Lyapunov函数：

式中，P为对称正定矩阵，其满足：

结合式(21)(22)可得：

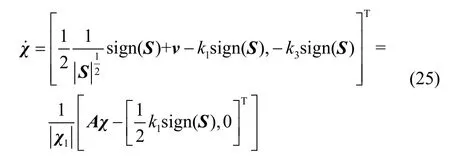
式(23)对时间求导可得：

对式(26)进一步分析可得：

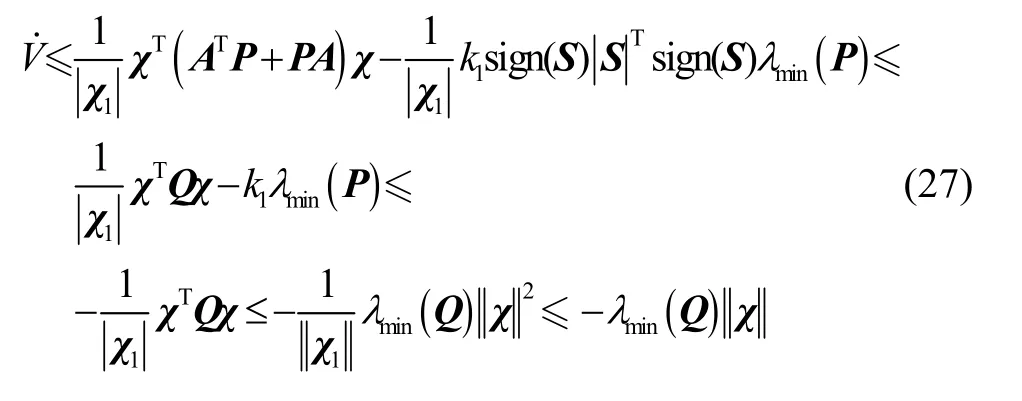
则：

由此可知：

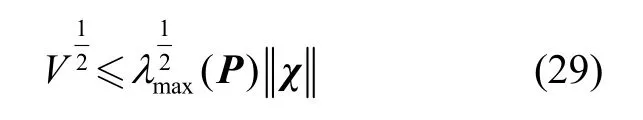
结合式(27)(29)可得：

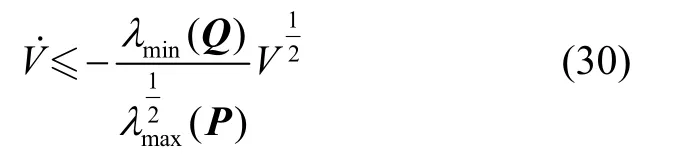
结合式(16)(30)可知，在有限时间内，式(21)所表示的闭环系统可收敛到零，即对于存在动力学不确定及外部扰动的系统，采用式(18)的控制输入，可以保证其有界且收敛。证毕！

2.3 阻抗控制外环设计

开启阻抗控制时，结合阻抗控制原理，并考虑空间机械臂系统动力学不确定及外部扰动，载体位置、姿态均不受控。空间机械臂系统动力学模型可写为：

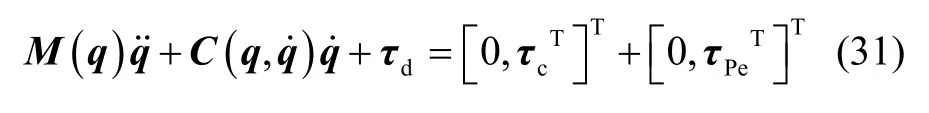
结合式(5)(6)可构成阻抗控制外环部分，由阻抗关系式根据部件插头输出力及力矩 pF与部件插头接触力及力矩 eF的误差在线修正末端运动轨迹，并获得输出力及力矩的跟踪。

将式(31)写成式(13)的形式，由此，对应的控制力矩可变为：

3 仿真模拟分析

为验证所提控制策略的有效性，采用图1所示模型仿真模拟。在仿真模拟中，可将孔内摩擦阻力及力矩等效为部件插头接触力及力矩，当部件插头输出力及力矩大于或等于孔内摩擦阻力及力矩时，即可进行插拔孔操作。同时，由于控制精度的问题，若直接以孔内摩擦阻力及力矩作为部件插头接触力及力矩带入阻抗模型，得到的部件插头输出力及力矩可能小于孔内摩擦阻力及力矩，导致插拔孔操作无法进行。由此，引入期望输出力及力矩，并选取期望输出力及力矩的数值略大于孔内摩擦阻力及力矩。

为保证插孔操作过程的精确控制，将插孔操作分为两个阶段，第一阶段，关闭阻抗控制，部件插头到达孔的正上方；第二阶段，开启阻抗控制，部件插头沿期望轨迹克服孔内摩擦阻力及力矩完成插孔操作。选取模型参数： m0= 50 kg ， m1= 4 kg ，m2= 4 kg ，m3= 2 kg ，mP= 5 kg ； L0= 1.5 m ，L1=3 m，L2= 3 m ，L3= 0.4 m ， LP= 0.2 m ； d1= 1.5 m ，d2= 1.5 m ，d3= 0.2 m ；I0= 35 kg·m2，I1= 2 kg·m2，I2= 2 kg·m2， I3= 1 kg·m2， IP= 5 kg· m2。定义有界扰动

仿真模拟包括三组：摩擦阻力及力矩不突变侧面插孔操作、摩擦阻力及力矩突变侧面插孔操作、摩擦阻力及力矩不突变正面拔孔操作。

3.1 摩擦阻力及力矩不突变侧面插孔操作

选取空间机械臂系统控制策略参数如下：KP=diag（ 355,355,355），BP=diag（300,300,300），MP=diag（1 ,1,1），k1=1，k2=5，k3=0.5，λ=16；假设在基联坐标系内，侧面孔口坐标［ 3 .6 m,-1 m ］T，侧面孔的深度h1= 0.1 m ，侧面孔轴线到载体底部的距离S1=1 m；为简化插孔操作，假设插孔过程仅存在沿插孔方向的摩擦阻力，摩擦力矩为0N·m，即Ff1=［18 N,0 N,0 N·m］T。

部件插头初始位置及姿态为：

仿真总时间为31.68 s，在0~5 s，关闭阻抗控制，调整部件插头位置和姿态，使其从初始位置到达孔的上方。在5~31.68 s，开启阻抗控制，调整部件插头位置和姿态，对准孔口，使其沿期望轨迹克服孔内摩擦阻力完成插孔操作。根据上述分段控制方案，仿真全程内部件插头的期望位姿如下：

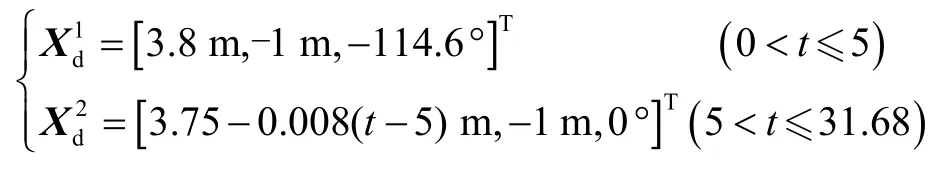
期望输出力如下：

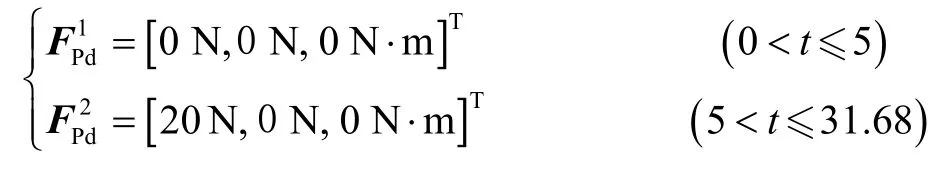
仿真结果如图3-6所示。图3为部件插头插孔轨迹，可知在进入孔口前一时刻，孔轴线方向的轨迹误差约为1 mm；进入孔口后，由于孔的位置约束，误差为0 mm。图4为部件插头插孔深度，其以孔口为参照，孔口外为负，孔口内为正。图5为部件插头输出力，可知插孔操作的整个过程，插孔方向的输出力大于摩擦阻力，力误差约为1 N。图6为部件插头姿态角变化情况，其跟踪误差小于0.5 °。

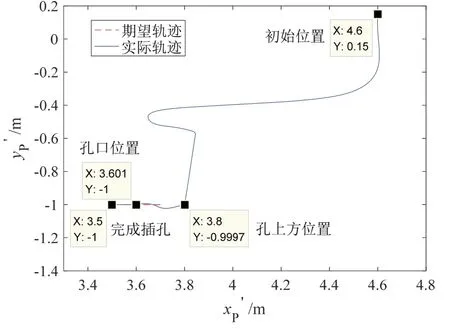
图3 部件插头插孔轨迹Fig.3 Trajectory of the end parts

图4 部件插头插孔深度Fig.4 Depth of the end parts

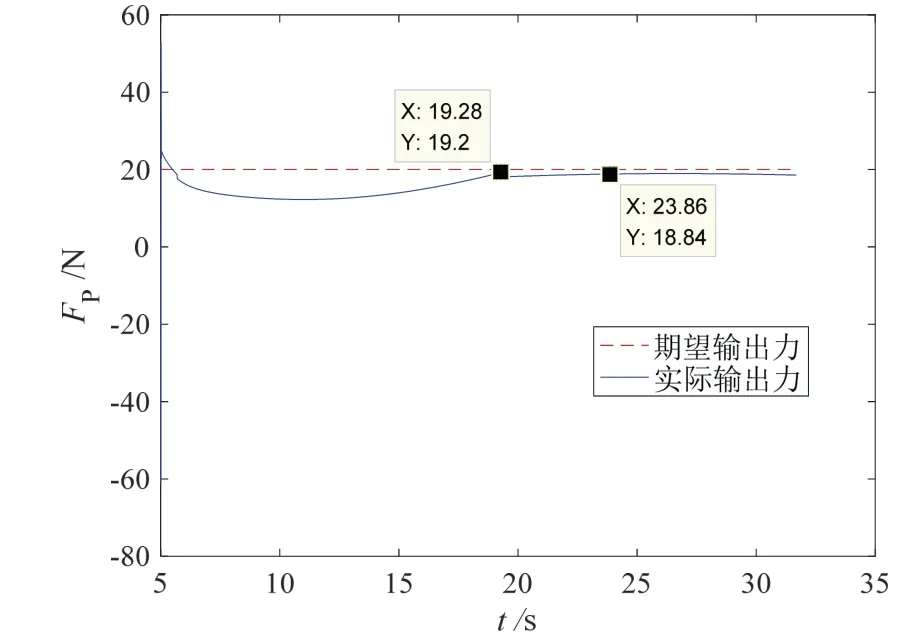
图5 部件插头输出力Fig.5 Output force of the end parts

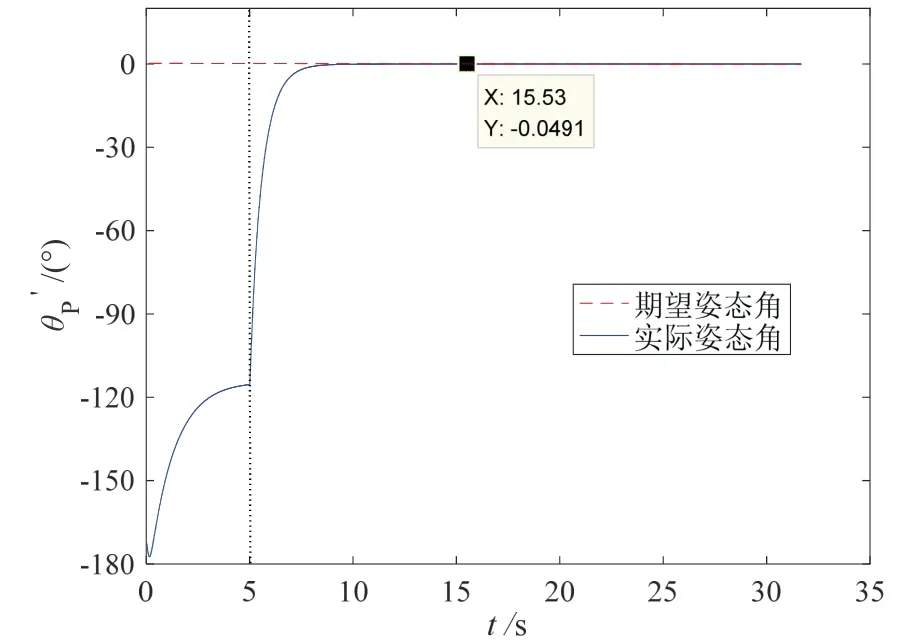
图6 部件插头姿态角Fig.6 Attitude angle of the end parts

3.2 摩擦阻力及力矩突变侧面插孔操作

选取空间机械臂系统控制策略参数如下：KP=diag（ 355,355,355），BP=diag（300,300,300），MP=diag（1 ,1,1），k1=1，k2=5，k3=0.5，λ=16；假设在基联坐标系内，侧面孔口坐标［ 3 .6 m,-1 m］T，侧面孔的深度h1= 0.1 m ，侧面孔轴线到载体底部的距离S1=1 m；为简化插孔操作，假设插孔过程仅存在沿插孔方向的摩擦阻力，摩擦力矩为0N·m，即Ff1=［18 N,0 N,0 N·m］T；考虑实际插孔过程摩擦阻力可能发生突变，即存在卡阻现象，可假设插孔深度为0.05m时，摩擦阻力突变为 30 N，此时

部件插头初始位置及姿态为：

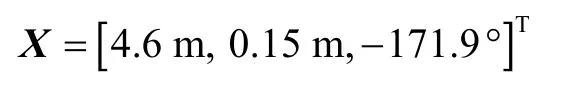
仿真总时间为39.69 s，在0~5 s，关闭阻抗控制，调整部件插头位置和姿态，使其从初始位置到达孔的上方。在5~39.69 s，开启阻抗控制，调整部件插头位置和姿态，对准孔口，使其沿期望轨迹克服孔内摩擦阻力完成插孔操作；特别地，在插孔深度为0.05 m，即25.35 s时，摩擦阻力发生突变，此时插孔操作停止，调整期望输出力，实际输出力线性增加，当其大于摩擦阻力，插孔操作继续，同时期望输出力调整为设定值。根据上述分段控制方案，仿真全程内部件插头的期望位姿如下：

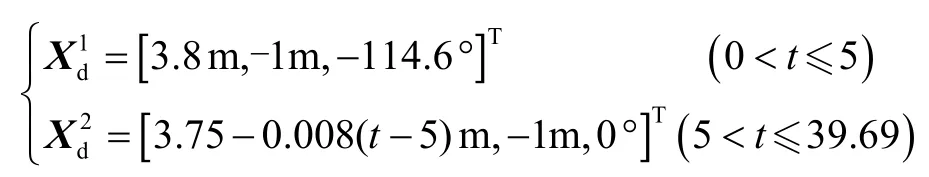
期望输出力如下：

仿真结果如图7-10所示。图7为部件插头插孔轨迹，可知在进入孔口前一时刻，孔轴线方向的轨迹误差约为0.1 mm；进入孔口后，由于孔的位置约束，误差为0 mm。图8为部件插头插孔深度，其以孔口为参照，孔口外为负，孔口内为正；可知在25.35~34 s，由于摩擦阻力发生突变，插孔操作停止，插孔深度保持不变。图9为部件插头输出力，在插孔操作的整个过程，插孔方向的输出力大于摩擦阻力，力误差约为1 N，且在摩擦阻力大小突变为30 N的情况下，输出力线性增加至大于30 N。图10为部件插头姿态角变化情况，其跟踪误差小于0.5 °。

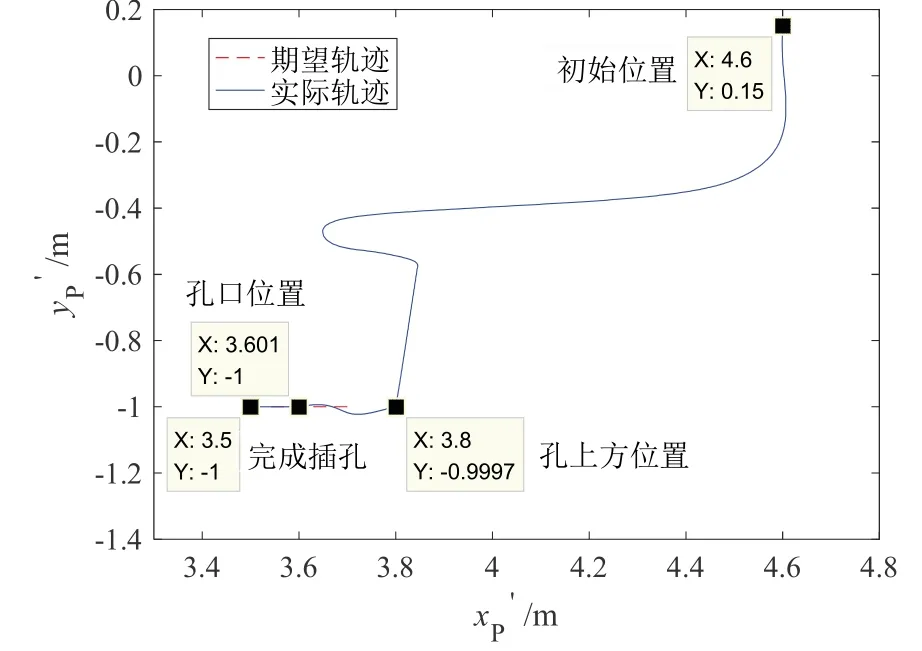
图7 部件插头插孔轨迹Fig.7 Trajectory of the end parts

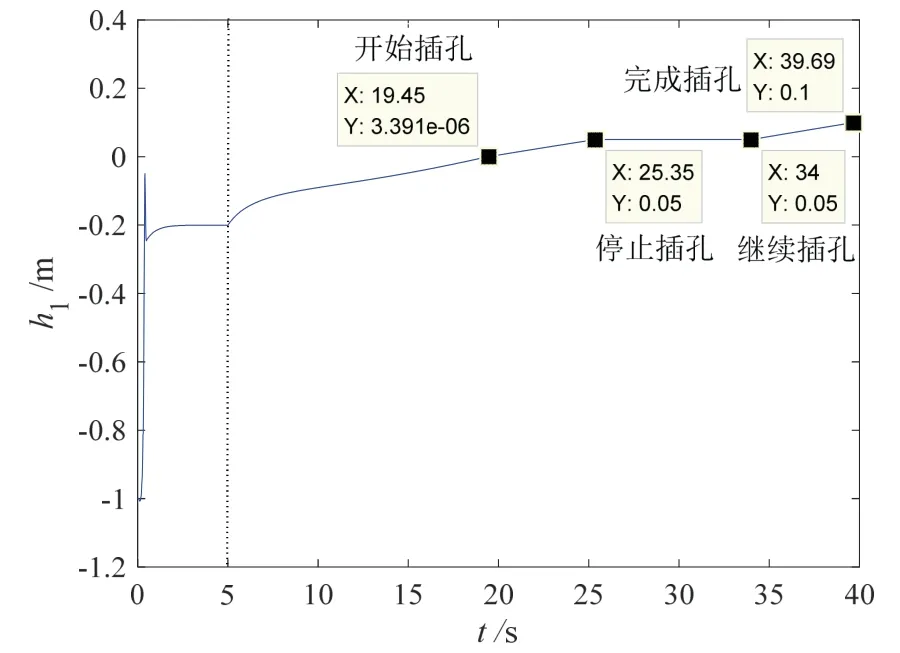
图8 部件插头插孔深度Fig.8 Depth of the end parts

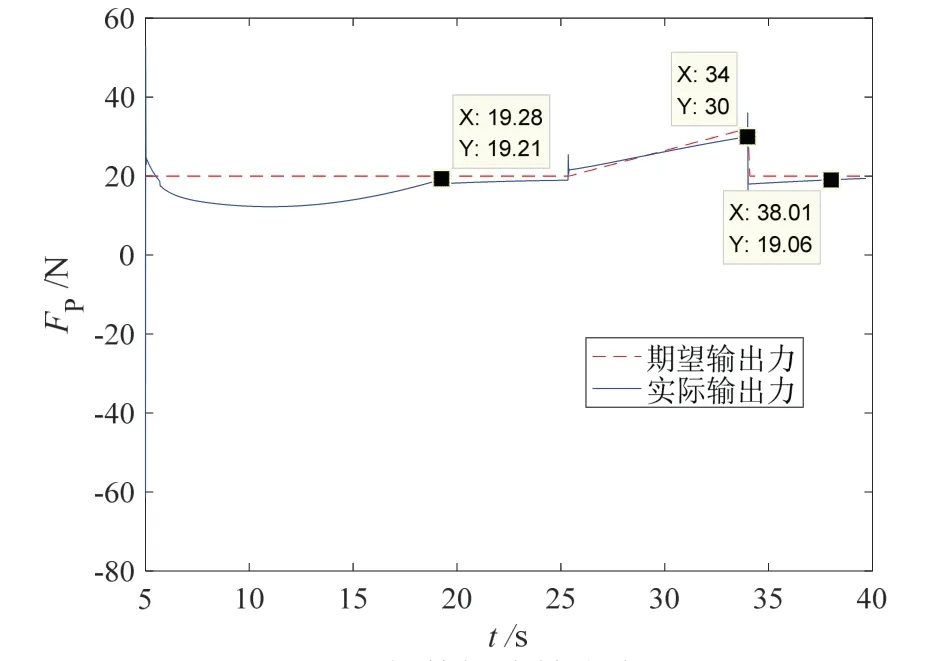
图9 部件插头输出力Fig.9 Output force of the end parts

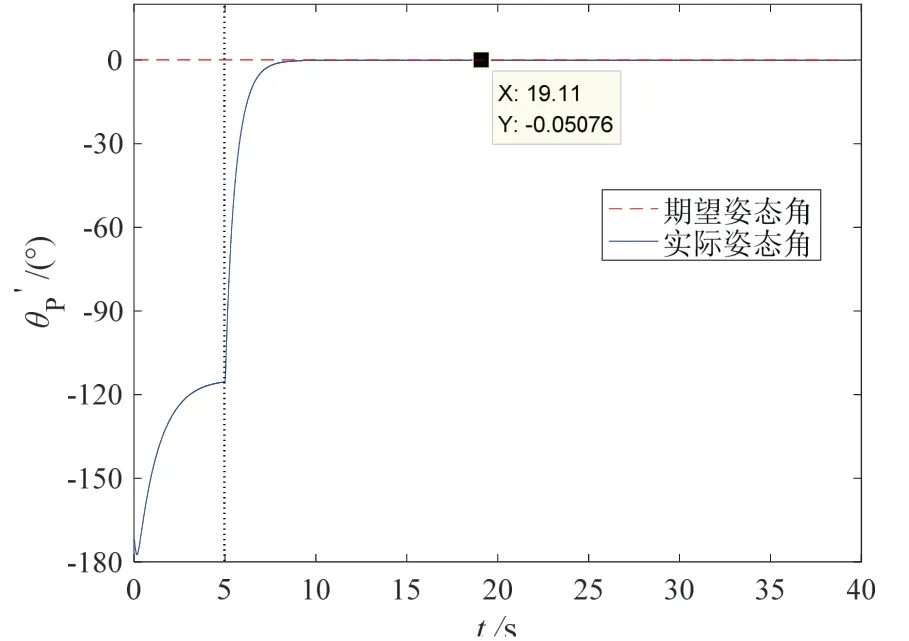
图10 部件插头姿态角Fig.10 Attitude angle of the end parts

3.3 摩擦阻力及力矩不突变正面拔孔操作

部件插头初始位置及姿态为：

仿真总时间为23.23 s，在0~8.68 s，开启阻抗控制，部件插头输出力线性增加至大于孔内摩擦阻力。在8.68~23.23 s，期望输出力调整为设定值，部件插头沿期望轨迹克服孔内摩擦阻力完成拔孔操作。根据上述分析，仿真全程内部件插头的期望位姿如下：

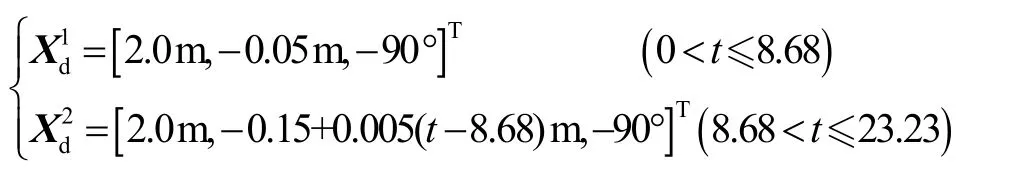
期望输出力如下：

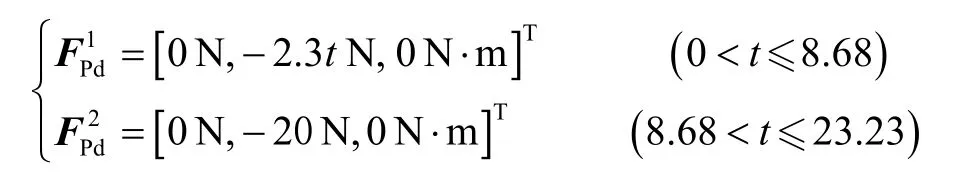
仿真结果如图11-14所示。图11为部件插头拔孔轨迹，可知由于孔的位置约束，孔轴线方向的轨迹误差为0 mm。图12为部件插头拔孔深度，深度以孔底为参照，向孔外为正，向孔内为负；可知在0~8.68 s，由于拔孔方向的输出力小于摩擦阻力，拔孔操作停止，拔孔深度保持不变。图13为部件插头输出力，可知在拔孔操作的整个过程，输出力大于摩擦阻力，力误差约为0.7 N。图14为部件插头姿态角变化情况。

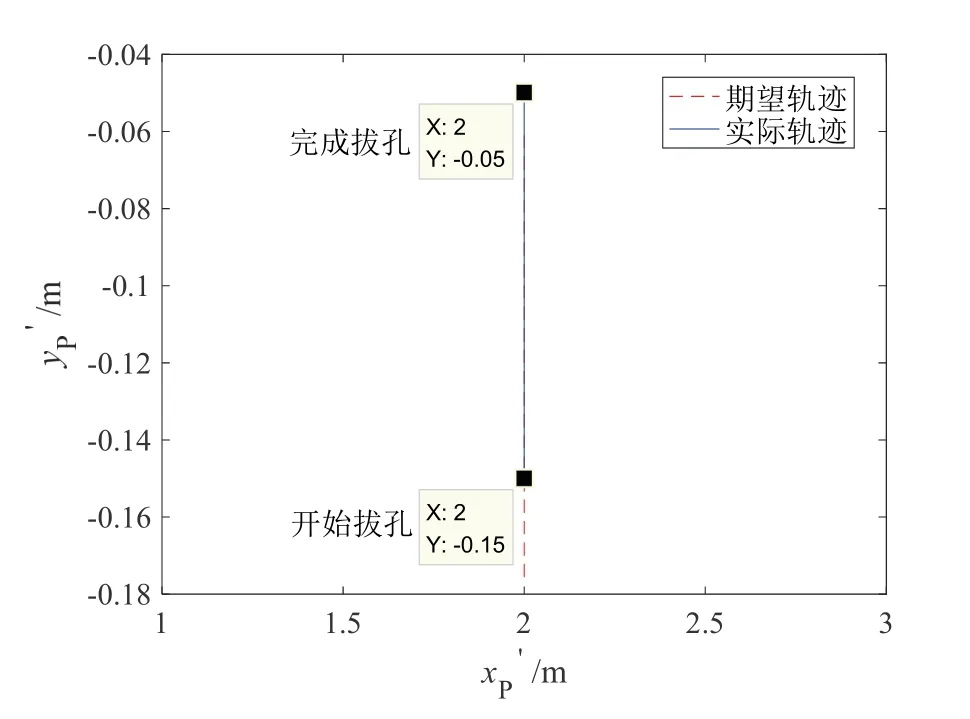
图11 部件插头插孔轨迹Fig.11 Trajectory of the end parts

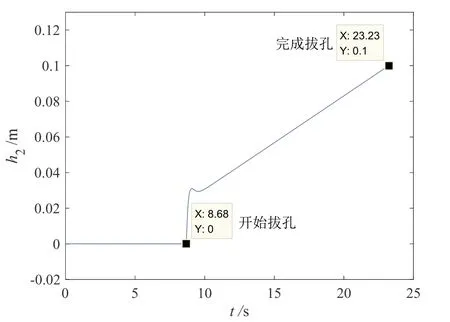
图12 部件插头插孔深度Fig.12 Depth of the end parts

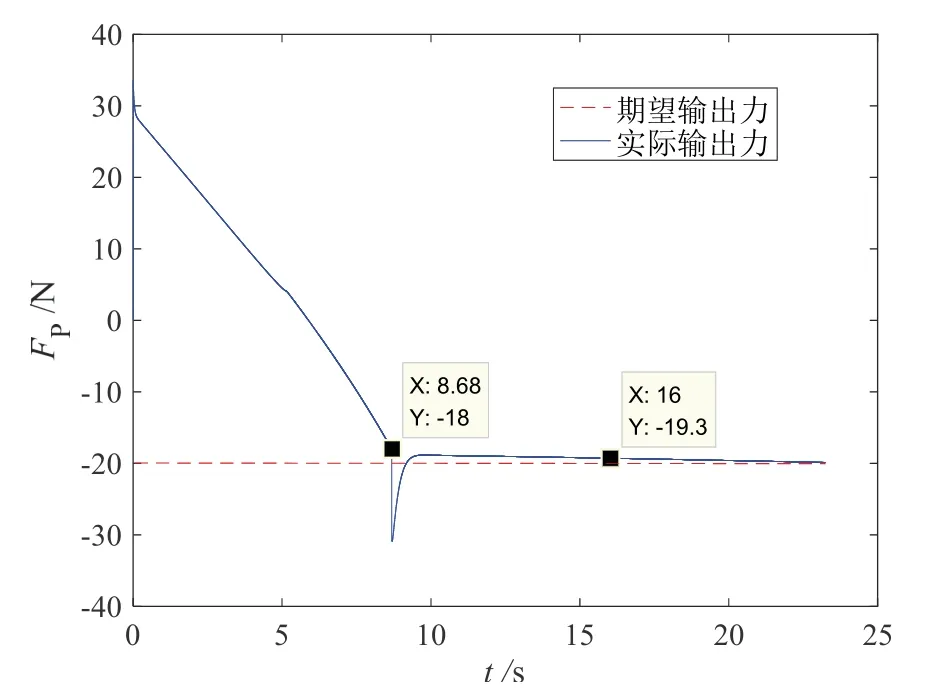
图13 部件插头输出力Fig.13 Output force of the end parts

图14 部件插头姿态角Fig.14 Attitude angle of the end parts

4 结 论

本文研究了空间机械臂在轨插拔孔操作的阻抗控制问题，建立了载体位置、姿态均不受控情况下系统动力学模型，设计了超扭曲滑模阻抗控制策略，并提出分段控制方案将插孔操作细分为两个阶段。上述控制策略应用于载体位置、姿态均不受控的空间机械臂在轨插拔孔操作，分析可得出以下结论：

(1) 结合阻抗控制，部件插头可以在基联坐标系内有效跟踪期望位姿并输出稳定力，实现空间机械臂在轨插拔孔操作。

(2) 在仿真模拟过程，部件插头位置精度均优于1 mm，姿态精度均优于0.5 °，输出力精度均优于1.5 N，均满足精度要求。

(3) 采用超扭曲滑模阻抗控制策略，在保证系统性能的同时，有效地抑制了抖振现象。

基于上述结论，本文也存在一些局限性及需要继续研究的内容，如：

(1) 根据仿真模拟分析可知，在摩擦阻力及力矩突变情况下，进行插孔操作的总时间为39.69 s，总的来说，操作时间较长，对空间站计算机资源占用较多。为此，需考虑如何有效减少插孔操作的时间。

(2)虽然超扭曲滑模阻抗控制策略的控制器结构较为简单，且具有良好的精度，但控制输入实时更新会使总体计算量略大一些。如何在保证精度的前提下减少控制输入的更新频率，仍是需要研究的内容。