基于扰动观测器的卫星姿态控制系统自适应有限时间容错控制

梁天添，王润泽，李科信，王英东，王 茂，周振华

（1. 大连交通大学 自动化与电气工程学院，大连 116028；2. 哈尔滨工业大学 空间控制与惯性技术研究中心，哈尔滨 150001；3. 常州工业职业技术学院，常州 213164）

姿态控制系统（Attitude Control Systems, ACSs）是卫星的重要子系统，由于卫星在恶劣工况下长时间运行，面临外部干扰、不确定性等诸多复杂因素的影响，其内部各子系统及零部件不可避免地面临可靠度降低的问题。卫星在轨飞行期间，其系统各部件的故障难以及时修复，因此，在有效地监测卫星的运行状态和及时估计系统故障的同时，对故障实施有效的容错控制，对于提高卫星在轨可靠性和安全性，减少安全隐患风险和防止系统灾难性事故发生具有重要意义。鉴于此，近年来，国内外诸多学者已深入研究了卫星ACSs的闭环容错控制问题。

故障估计作为故障诊断的最后一步，其结果与容错控制紧密相关[1]。因此，已有学者基于故障估计结果研究了卫星ACSs的容错控制问题[2-4]。但是，上述研究中的容错控制方法需要预先估计出故障的信息，在容错控制的实时性上有待提高。为此，基于自适应算法的快速收敛特性，自适应容错控制方法已被应用到卫星ACSs[5,6]。进一步，考虑到卫星ACSs的有限时间稳定性（Finite Time Stability, FTS）和有限时间有界性（Finite Time Boundness, FTB），终端滑模控制[7-9]已被学者用于ACSs的主动容错控制中。另外，已有学者将自适应算法应用于ACSs的有限时间容错控制中[10-12]，有效提高了闭环容错控制的性能。

上述文献针对ACSs容错控制问题的研究，较少考虑了外部干扰未知情况下的系统容错控制性能。事实上，由于系统的外部干扰多具有未知特性，需首先获得其信息，进而快速补偿执行器故障，提高容错控制性能。为此，扰动观测器方法[13,14]已被用于未知扰动的估计，进而实现了ACSs的有限时间复合主动容错控制。然而，上述研究仍有进一步提升的空间。作为ACSs难以忽视的重要因素，系统时滞需要在容错控制中加以考虑。尽管已有学者基于扰动观测器，研究了具有输入时滞ACSs的复合容错控制问题[15,16]，但这些研究仅限于系统的渐进稳定性分析，而对于具有状态时滞ACSs的有限时间复合容错控制，目前仍较为少见。

据以上分析，本文基于前期的研究成果[17,18]，结合自适应算法和FTB分析，针对具有状态时变时滞、不确定性、外部可建模扰动、运行噪声和未知执行器故障的卫星ACSs系统，提出基于扰动观测器的自适应有限时间复合容错控制策略。与已有方法相比，本文主要创新点可概括为：1）综合考虑了系统状态时变时滞、不确定性、外部可建模扰动等复杂因素对容错控制性能的影响，拓展了复杂非线性系统的容错控制范围；2）设计的时滞依赖主动容错控制器包含反馈控制项、可建模扰动补偿项和故障补偿项，在实现闭环系统容错控制的同时，可快速有效地估计可建模扰动值；3）设计的自适应估计算法实现了故障的快速补偿，从而进一步提高了有限时间内的卫星ACSs时变时滞系统模型闭环容错性能。

本文首先基于非线性ACSs，考虑系统状态时变时滞、不确定性、可建模扰动和未知有界执行器故障的影响，针对可建模扰动设计扰动观测器，得到扰动误差系统。其次，设计时滞依赖的复合自适应有限时间容错控制器（Composite Adaptive Finite Time Fault-Tolerant Controller, CAFTFC），并设计控制器中的故障补偿自适应率，建立闭环容错控制系统模型。然后，分析闭环系统的FTB性能，讨论闭环测量输出对于系统不确定性、运行噪声、执行器故障及其误差和导数的鲁棒性。再次，给出观测器和控制器增益限制矩阵存在的充分条件及该限制矩阵的线性矩阵不等式（Linear Matrix Inequality, LMI）形式。最后，给出卫星ACSs执行器故障模型，利用设计的CAFTFC仿真，并与非复合的自适应有限时间容错控制器（Adaptive Finite Time Fault-Tolerant Controller,AFTFC）进行对比分析，以验证提出方法的有效性。

1 问题描述

考虑如式(1)所示的卫星ACSs：

令 x(t) =ω(t)，考虑系统状态变量中的时变时滞环节、不确定性因素和卫星运行过程中的噪声影响，则由式(1)得到：

其中，x(t) ∈Rn为状态向量，l(t)代表状态时变时滞，且满足l(t)≤h，l˙(t)≤τ ，h和τ为正标量；u(t) =Tc∈RP为系统输入， d(t) =Td∈Rr表示可建模扰动，v(t) ∈Rυ表示运行噪声，它们的分布矩阵D和E为适当维数的常数矩阵，考虑到干扰和噪声可能并非发生于每一维。g(t,l(t))表示含有时变时滞的非线性项，且为范数有界变量，即：

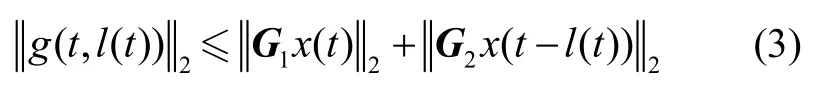
其中， G1和G2为适当维数的矩阵； y(t) ∈Rm为系统的测量输出，ΔA、ΔAd分别为状态及状态时滞的不确定性，且满足：Δ A = M1F1(t)N1，Δ Ad= M2F2(t)N2，Mi, Ni, i= 1,2为适当维数的已知矩阵，未知矩阵 Fi(t)满足：另外，系统(2)中，非线性项g(t,l(t))和系数矩阵A、 Ad、B、C的具体形式为：g(t,l(t )) = αφ( t ) + βφ(t - l(t ) ) - Ax (t ) - Adx(t -l(t ))，

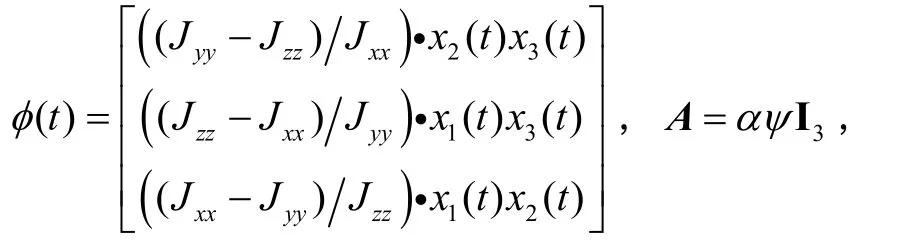
Ad=βψI3， B=diag(1/ Jxx,1/ Jyy,1/ Jzz)， C = I3，其中，ψ表示选取的常数，α和β表示时滞程度，且满足：α +β= 1， φ (t- l(t))与φ(t)具有相同的形式，仅将t替换为t-l(t)。

假设系统的执行器发生未知有界故障，则系统(2)可重新表示为：

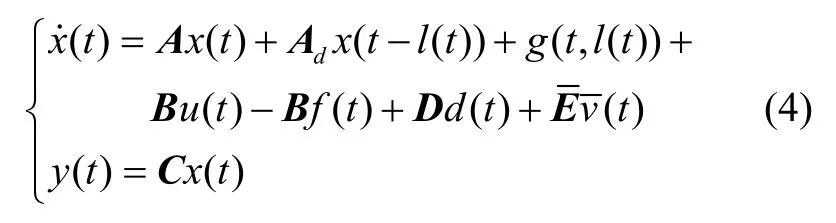
将可建模扰动d(t)建模为：

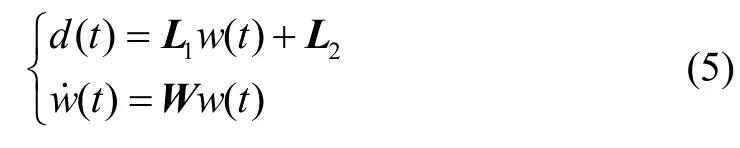
其中， w(t) ∈Rq为未知扰动，系数矩阵 L1、 L2与干扰幅值有关；W1与干扰频率有关。

针对未知扰动w(t)，设计如式(6)所示的观测器：

其中，H为待设计的增益矩阵。

由式(4)(5)(6)可得：

首先提出如下假设及引理。

假设1rank(B ) =rank( ［ B D］ )。

引理1[19]若假设1成立，则存在矩阵 B*，使得：

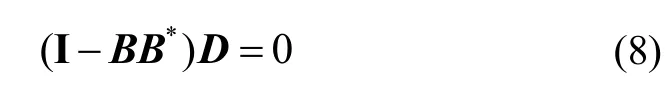
2 复合自适应有限时间容错控制器设计

针对系统(4)，设计时滞依赖容错控制器(9)：

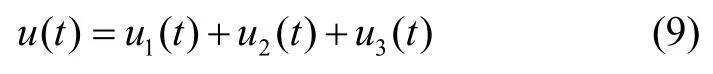
其中，u1(t)、u2(t)和u3(t)分别代表系统(4)的反馈控制项、可建模扰动补偿项和故障补偿项，且分别满足：

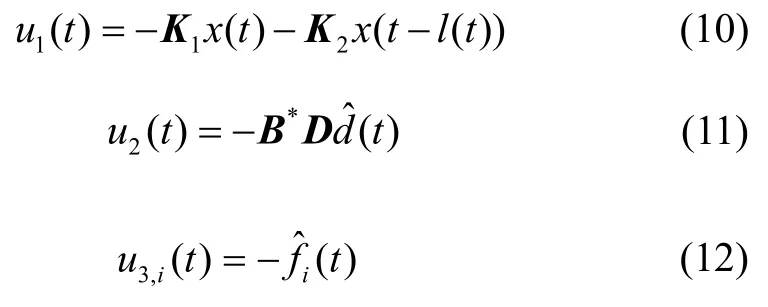
考虑引理1，将式(7)中第一个方程和式(9)代入式(4)可得：

2)y(t)对于Lyapunov-Krasovskii函数初值V(0)、系统不确定性、运行噪声、执行器故障及其误差和导数具有鲁棒性，即：

首先给出与推导及证明相关的定义及引理。

定义1[18]给定标量c1＞ 0，T＞0，矩阵U＞0，系统(14)关于(c1， c2，T， U，v )是FTB的，如果：

引理2[18]对于任意实矩阵a、b及Ω(t)，若有：

成立，则有：

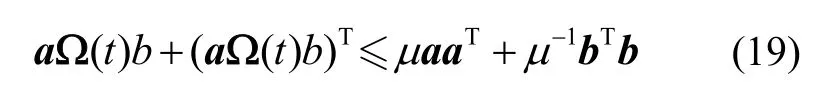
其中，μ为任意正标量。

对于矩阵Σ，定义： sy(Σ)=Σ+ΣT；基于上述讨论，提出定理1。

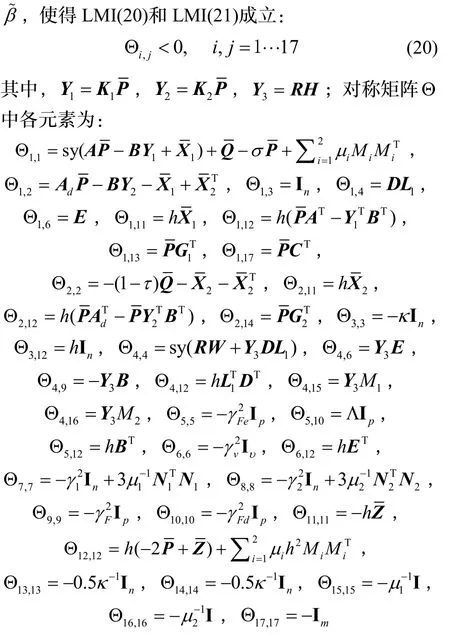
其他各元素均为零；

则条件1)和条件2)同时得到满足。

证明：选取如式(22)所示的Lyapunov-Krasovskii函数：

其中，V1(t)代表与状态变量有关的函数，V2(t)和 V3(t)代表与时滞变量有关的函数，V4(t)代表与扰动估计补偿项有关的函数，V5(t)代表与故障补偿项有关的函数，它们的具体形式为：

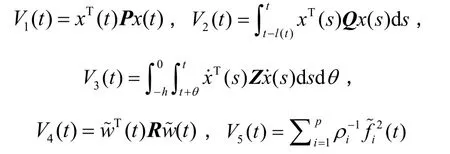
对式(22)中V1(t)、V2(t)和V3(t)求导可得：

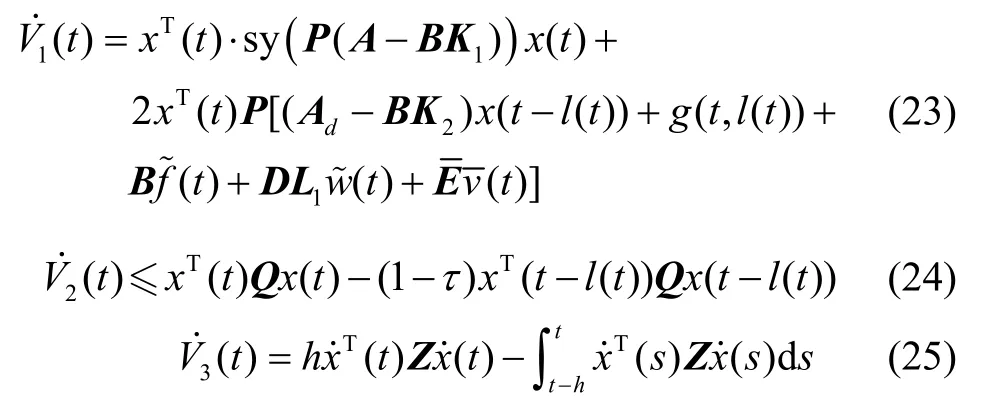
由式(7)中第二个方程可得：

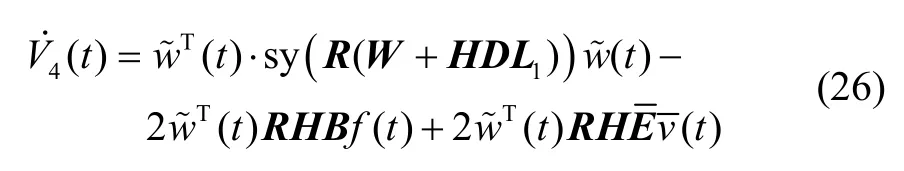
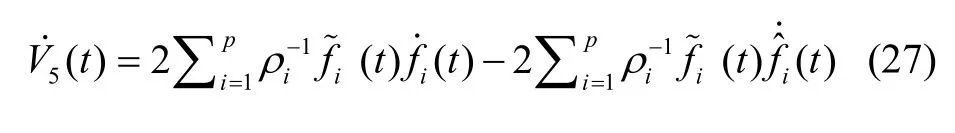
另外，由式(3)可知，存在正标量κ，使得：

由牛顿-莱布尼茨公式可知，存在适当维数的矩阵X1和X2，使得：

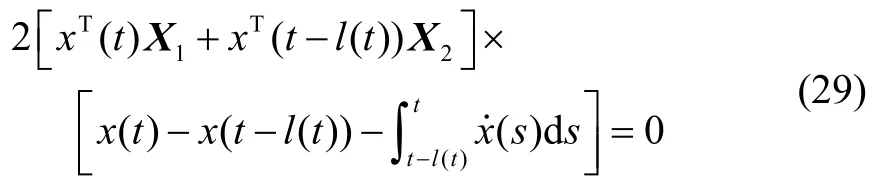
故式(25)可重新改写为：

其中：

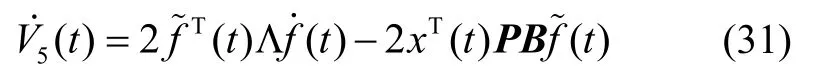
基于式(23)-(31)，有不等式(32)成立：

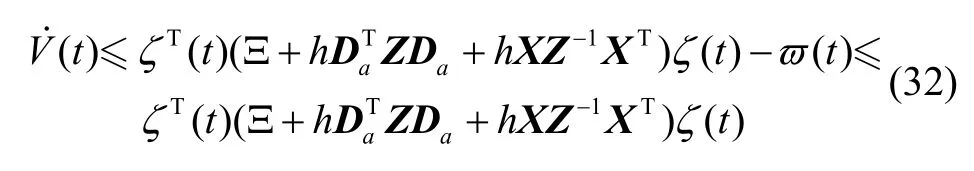
其中：

*代表矩阵中的对称元素。

另外，易知： -σ V (t ) ≤ - σ V1(t )，即：

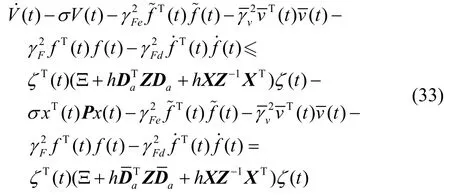
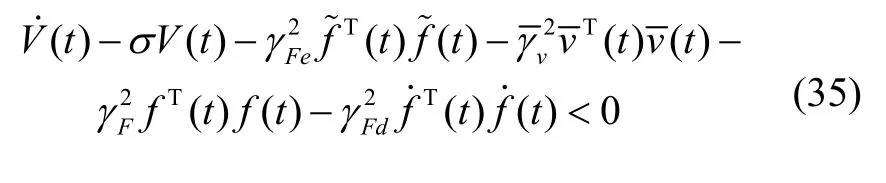
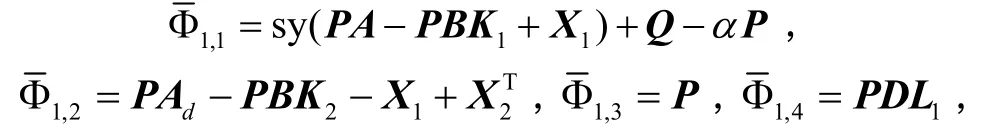
基于Schur补引理及引理2，则式(36)等价于：

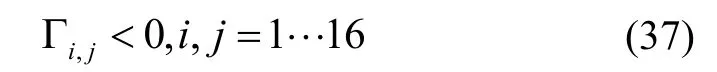
其中：

其它各元素均为零。

另一方面，式(20)可重新表示为：

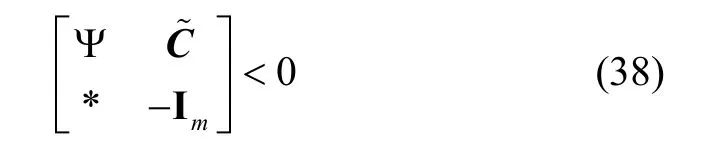
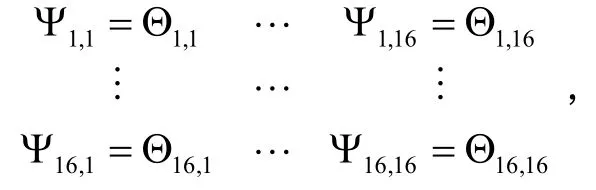
其中，Ψi,j，i, j=1… 1 6中各元素为：

即，若有式(20)成立，则有：

由式(21)可知：

式(49)符合定义1，即若有定理1成立，则有条件1)得到满足。

进一步，基于Schur补引理，式(20)等价于：

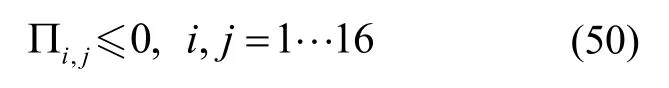
将式(50)的两边相继左乘及右乘式(41)和式(42)，基于Schur补引理，则式(50)等价于：

对式(51)从0到T积分，由Gronwall不等式可得：

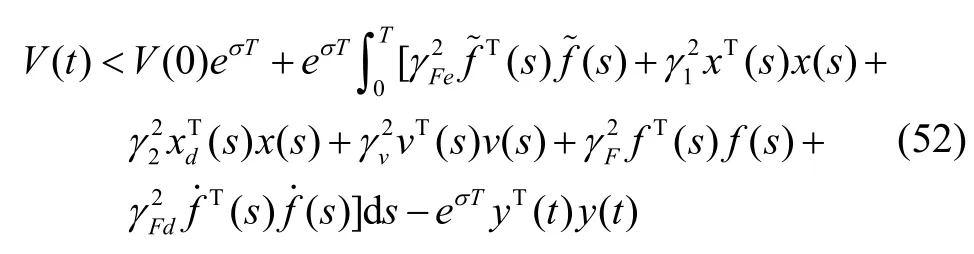
因V(t)≥0，故式(52)可改写为：

即，若有定理1成立，则条件2)得到满足。

综上所述，式(20)(21)使得条件1)和2)同时满足，定理1证毕。

基于上述讨论，给出基于扰动观测器的CAFTFTC设计流程。

算法1 基于扰动观测器的CAFTFTC设计流程。

步骤1：给定c1、T、U、ε1、ε2、εv、εF、和。

步骤2：解下列凸优化问题：

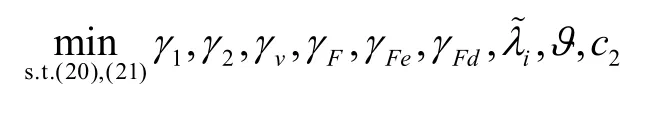
步骤4：执行闭环容错控制。

3 仿真算例

在本节中，给出一个如式(2)所示的卫星ACSs[18]，假设模型的状态时变时滞为： l(t ) = 0.4sin(t)，α= 0.85， β= 0.15。与不确定性有关的系数矩阵为：M1=M2= ［0.2 0.2 0.2］T，N1=N2= ［1 1 1］，与A和 Ad有关的常数ψ选取为：ψ=0.3。

执行器失效故障因子 LF满足：LF= diag(0.4,0.1,0.5)，与可建模扰动d(t)相关的系数矩阵为：

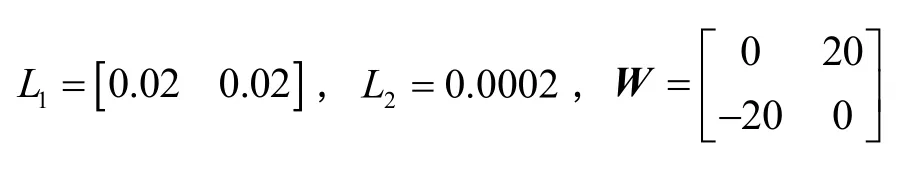
折衷考虑观测器的估计精度和系统鲁棒性，令α= 3.2，得到γFe、 γv、γ1、 γ2、γFd和 γF的值为：γFe=0.58、 γv=0.64、γ1=0.58、γ2=0.72、 γFd=0.71和 γF= 0.76。

由定理1计算分别得到扰动观测器系数矩阵H和控制器系数矩阵K1、K2为：

为验证设计方案的有效性，首先将可建模扰动和运行噪声视为系统的整体干扰，基于非复合的自适应有限容错控制器（Adaptive Finite Time Fault-Tolerant Controller, AFTFTC）进行仿真，然后利用本文设计的CAFTFTC进行仿真，并与AFTFTC的仿真结果进行对比。当系统发生执行器故障时，状态变量及可建模扰动的估计结果如图1及图2所示。状态估计及可建模扰动估计均方根误差（Root Mean Square Error,RMSE）如表1及表2所示。

图1 状态变量及其估计结果Fig.1 State variablesand their estimations

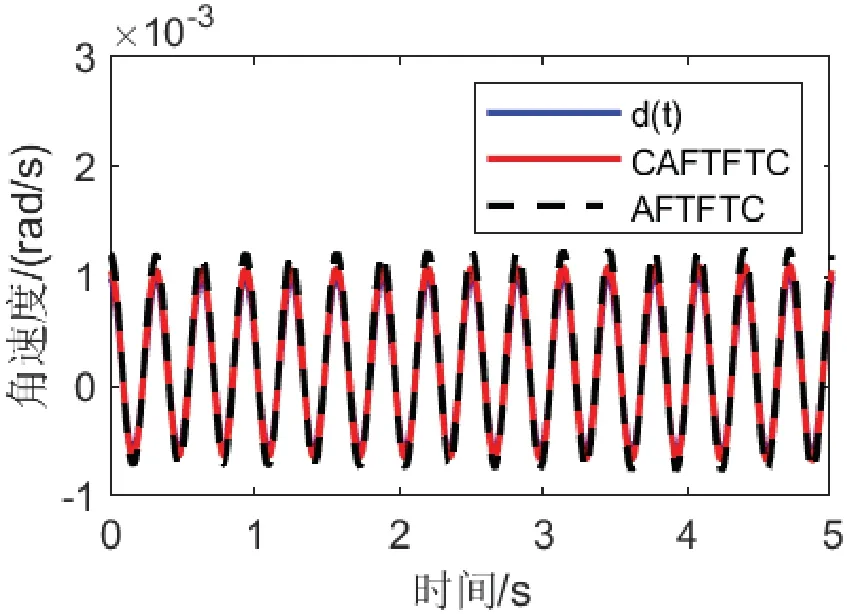
图2 可建模扰动及其估计结果Fig.2 Modeled disturbanceand itsestimation results

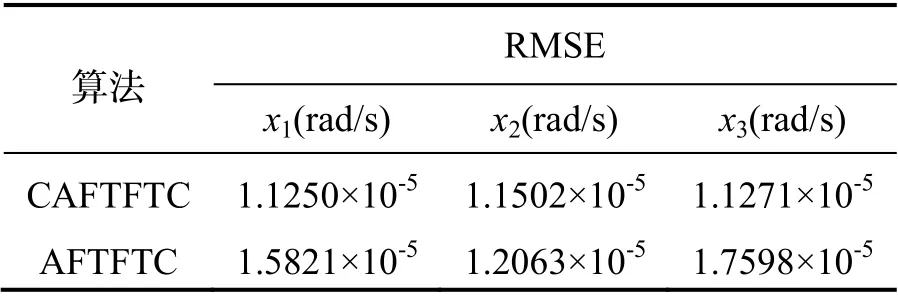
表1 状态变量估计RMSETab.1 RMSEof statevariablesestimation

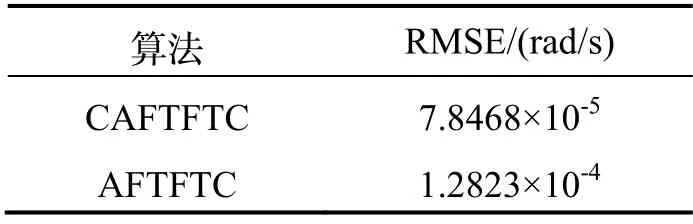
表2 可建模扰动估计RMSETab.2 RMSEof modeled disturbanceestimation

由图1及图2可知，当时变时滞系统存在执行器故障、不确定性、可建模扰动及噪声时，本文设计的CAFTFTC相较于AFTFTC，不仅能够更好地实现卫星ACSs的闭环容错控制，而且能够更精确地估计出可建模扰动的真实值。表1及表2进一步验证了其精确性，从表中可知，相较于AFTFTC，CAFTFTC对于状态变量的估计RMSE分别降低了28.9%、4.7%和36.0%；对于可建模扰动的估计RMSE降低了38.8%。仿真结果表明，尽管ACSs状态变量中存在时变时滞环节，因本文提出的复合容错控制策略，能够有效地估计可建模扰动的真实值，从而能更好地实现卫星ACSs的闭环容错控制。仿真验证了设计方案的有效性。

4 结论

本文针对卫星ACSs的有限时间闭环容错控制问题，提出了一种基于扰动观测器的复合自适应容错控制器方案。建立了扰动误差系统，设计了时滞依赖控制器，该控制器包含反馈控制项、扰动补偿和自适应故障补偿项，在FTB条件及有限时间鲁棒H∞条件下，给出了观测器和控制器增益限制矩阵的LMI形式，并利用对比仿真验证了设计方案的有效性。仿真结果表明，针对具有执行器故障和状态时变时滞的卫星ACSs，设计的CAFTFTC不仅可以在有限时间内更好地执行闭环容错控制，而且能更有效地估计可建模扰动。

尽管如此，本文研究方法仍有进一步的改进空间。相较于基于传统模型的方法，深度学习神经网络方法具有更好的收敛速度及估计精度。因此，基于不确定时变时滞系统模型，结合自适应算法和深度学习神经网络，改进控制器中的故障补偿策略，以更好地实现有限时间内卫星ACSs的闭环容错控制，具有理论和现实意义。本文的设计方案可为后续基于深度学习神经网络的不确定时变时滞卫星ACSs自适应有限时间容错控制器设计提供理论基础。