一种基于障碍物登陆点检测的全局路径规划算法

王 磊，王 毓，孙力帆

（1. 河南科技大学 国际教育学院，洛阳 471023；2. 河南科技大学 信息工程学院，洛阳 471023）

人工智能时代的机器人已不再充当简单的指令执行角色，而是朝着智能化、高效化的方向发展，它代表了高科技的发展前沿，已经在各行各业中得到广泛应用。路径规划是移动机器人研究领域的热点，具有重要的理论与现实意义，其主要任务是使机器人能够成功避开环境中的各种障碍，并沿着最低代价的路径到达终点。依据机器人对地图信息的掌握情况可将算法分为全局路径规划与局部路径规划。其中，A*（A-Star）[1-3]是一种经典的全局路径规划算法，它是Dijkstra算法[4-6]与宽度优先搜索（Breadth First Search,BFS）算法[7]的结合，是一种启发式搜索算法。A*算法利用启发函数指导寻路过程，通过计算栅格地图各结点的代价值，选取待扩展的最佳结点，直至找到最终目标点位置，该算法以超强的环境适应能力获得了非常广泛的应用，但缺点是随着地图规模的扩大，待搜索结点数量大幅增加，路径规划时间变得过于漫长。

为了解决A*算法在大场景地图中的搜索时间问题，前人进行了各种改进。双向A*（Bidirectional A-Star）算法[8]采用正反向交替机制，分别从起点和终点朝着相对方向进行搜索，最终在起点、终点连线的中点区域汇合，可找到最短路径，提升搜索效率。加权A*（The weighted A-Star）算法[9]通过寻找权重和启发项之间的关系选择最佳权重值，后来又提出了基于起点和目标点之间长度与权重集相关联的动态加权方法，还有基于路径成本与权重集相关联的方法，这些方法虽能提升寻路效率，但结果不稳定，不能很好地平衡路径代价与搜索时间之间的关系。Theta*[10]是一种任意角度的寻路算法，可以找到比A*更短的路径，它在A*基础上增加了结点之间的可见性检测，每扩展一个结点都要先计算该结点与相关结点是否可见，因而增加了计算量，比A*耗时更长。松弛A*（Relaxed A-Star）算法[11]用到达结点n的第一条路径成本来近似从起点到n的所有路径成本，即g(n)只被计算一次，省略了原A*算法多次比较g(n)、更新g(n)的步骤，因此搜索时间缩短，但不能保证找到最优解。Harabor D等人于2011年提出了跳点搜索（Jump Point Search, JPS）算法[12-15]，该算法改进了A*的无差别扩展规则，只扩展有代表性的特殊栅格点，从而大大降低了结点访问量，使算法效率得到大幅提升。以上算法仅在A*算法的规则层面进行了改进，并未考虑到障碍物在地图中的整体分布情况，仍然处于盲目搜索阶段。为了降低搜索过程的盲目性，本文提出了一种障碍物登陆点检测方法，利用障碍物分布信息寻找登陆点，将结点扩展范围缩小至障碍物边缘区域，从而减少结点访问数量，再利用改进的Dijkstra算法搜索最短路径，进一步提高路径规划效率。

1 障碍物登陆点检测算法实现

1.1 障碍物登陆点检测算法主要思想

在地图中规划最短路径，路径转折点一般位于障碍物的边缘区域，如能够检测出起点至终点所有可能经过的障碍物边缘区域，不仅覆盖了最短路径的拐点，而且极大缩小了路径规划范围，可减少冗余结点数量，提高算法效率。本文首先引入一个概念，在栅格地图中相邻的障碍栅格点组成一个整体区域，称为障碍物块[16]。当起点、终点连线被障碍物块阻挡时，最短路径一定经过该障碍物块的某一边缘点附近，本文将这一边缘点定义为登陆点，该点由起点、终点的连线与相交障碍物块的位置关系共同决定。

定义1：如图1所示，连接起点S与终点E，直线SE与障碍物块B1碰撞于A点，以起点S作为定点，将A点向障碍物块 B1的两侧移动，当角度θ1与θ2最大时，对应栅格点O1L与O1R即为障碍物块 B1的左、右登陆点。

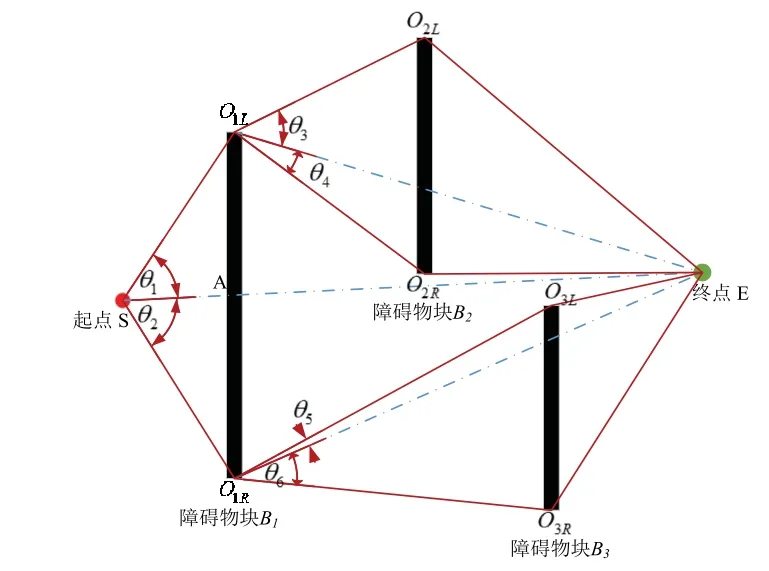
图1 登陆点分布图Fig.1 Distribution diagram of landing nodes

图1 中，检测到点O1L与O1R是障碍物块B1的登陆点，再将O1L作为起点，E作为终点，直线O1LE与障碍物块 B2发生碰撞，通过计算θ3与θ4的最大值可得到障碍物块 B2的登陆点是O2L与O2R，再将O1R作为起点，E作为终点，直线O1RE与障碍物块 B3发生碰撞，通过计算θ5与θ6的最大值可检测到障碍物块B3的登陆点是O3L与O3R，如此可计算出相关障碍物块的登陆点O1L、O1R、O2L、O2R、O3L、O3R，使用递归算法检测所有障碍物登陆点，流程图如图2所示。

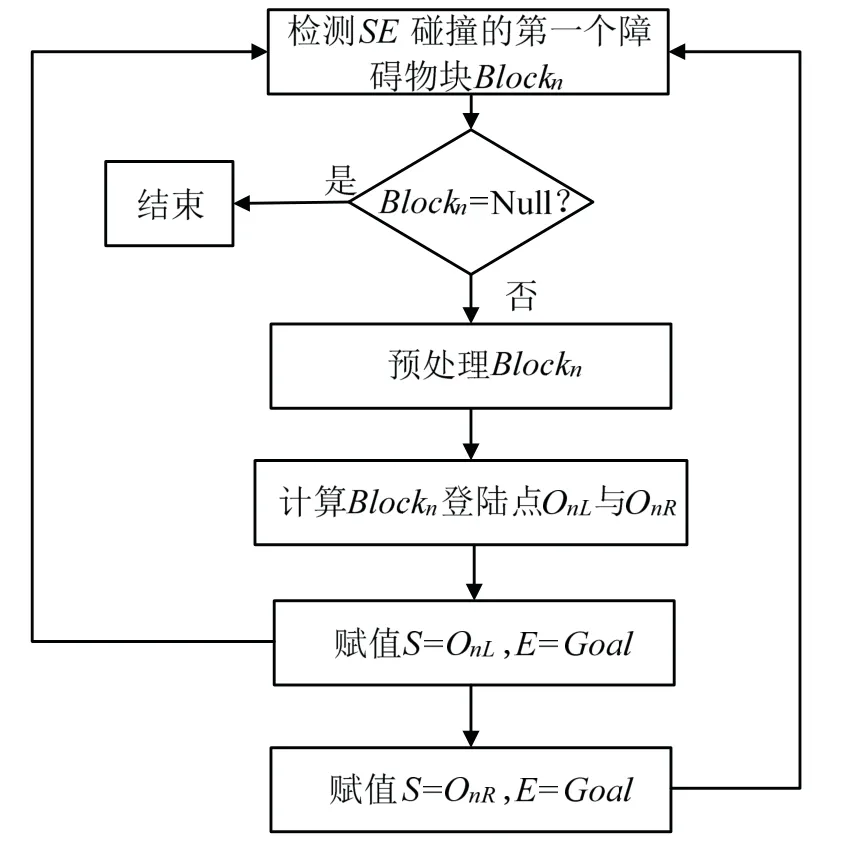
图2 登陆点递归检测流程图Fig.2 Flow chart of landing nodes recursive detection

1.2 构建障碍物块

遍历地图中所有栅格点，将上下左右相邻的障碍物栅格标记到同一个集合中，直到完成所有障碍物栅格的分类，最终形成多个障碍物块，如图3所示。具体操作步骤如下：

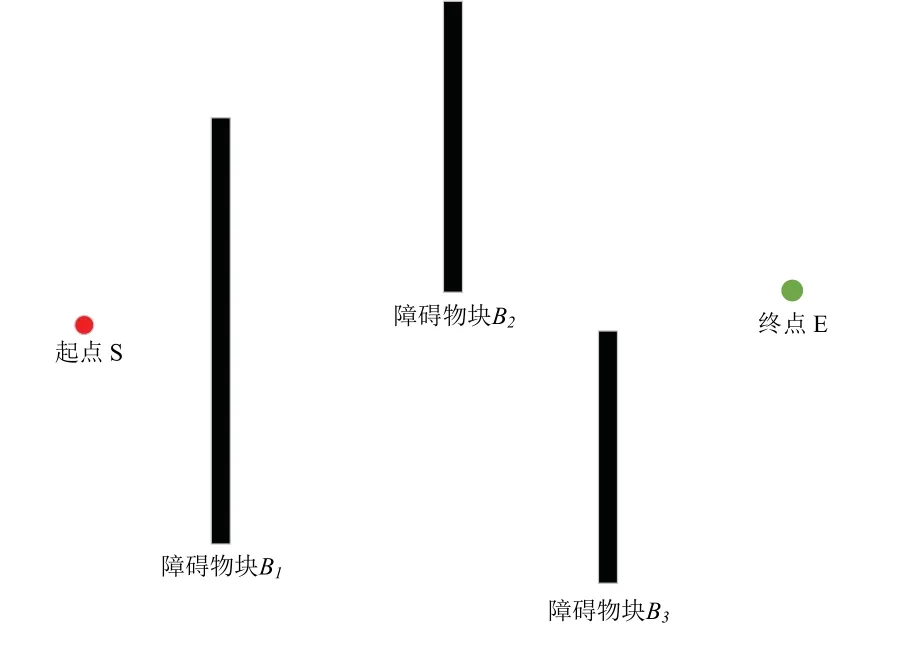
图3 障碍物块示意图Fig.3 Diagram of obstacle blocks

Step1:建立栅格地图对应的二维数组G、存放待检测结点列表 Lobstacle、当前障碍物块 Bobstacle以及障碍物块列表LOB；

Step2:检测当前栅格点，如果是障碍物，则将当前栅格点存入列表 Lobstacle中，并将当前栅格点在数组G的相应位置写入true；

Step3:检测列表 Lobstacle，如 Lobstacle为空，进入Step4，否则检测 Lobstacle中第一个结点的8邻域栅格点，如检测到障碍物且该障碍物在数组G中的对应值为false，则将该障碍物插入列表 Lobstacle中，并将数组G的对应位设置为 true，同时将 Lobstacle的第一个结点加入Bobstacle中，然后删除 Lobstacle中第一个结点，循环执行Step3；

Step4:将 Bobstacle插入列表LOB，如数组G中所有值均为true，则程序结束，否则进入Step2。

1.3 障碍物碰撞检测

如何快速检测直线与障碍物的碰撞点是寻找登陆点的第一步。可利用起点与终点坐标，依据两点式直线方程实现碰撞检测。首先通过起点与终点坐标建立直线方程，然后从起点开始向终点进行碰撞检测。设起点为 D1，终点为 D2，移动步长为λ，在直线D1D2上由起点向终点方向移动检测，检测直线上的点( xn, yn)是否位于障碍物栅格内，如位于障碍物栅格内部，则发生碰撞，如移动到终点 D2仍未发现障碍物栅格，则称点 D1与 D2可直达。如图4所示，栅格坐标即为栅格中心点，其中黑色栅格(3,3)为障碍物，从起点 D1(1,0)（黄色栅格）到终点 D2(5,5)（红色栅格）检测障碍物，设置步长λ=0.1，利用直线D1D2方程计算对应栅格坐标如式(1)所示：

图4 障碍物碰撞检测Fig.4 Obstacle collisiontest

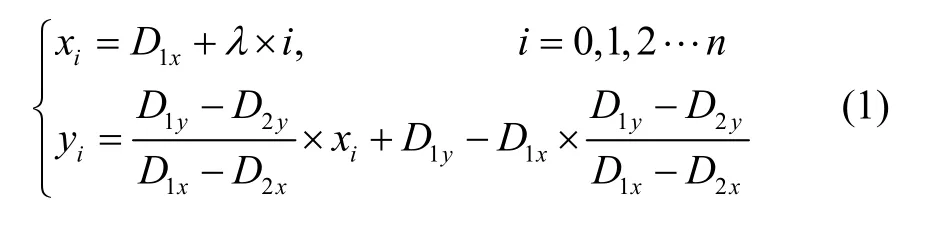
其中，D1x为点 D1的X轴坐标，D1y为点 D1的Y轴坐标，D2x为点 D2的X轴坐标，D2y为点 D2的Y轴坐标。当 xi⊂ [3,3.5]时，可计算出 yi⊂ [2.5,3]，即直线D1D2上的点(xi,yi)位于障碍物栅格(3,3)区域内，因而检测到直线D1D2与障碍物栅格(3,3)发生碰撞，依据此方法可快速判断出地图中的任意两点是否可直达。

1.4 计算障碍物映射角

图5 中，连接起点S与终点E，则直线SE与灰色障碍物块发生碰撞，然后分别连接起点与障碍物块所有可直达边缘点。设向量与的夹角为θ，由点积公式可知，且

图5 障碍物映射角Fig.5 Mapping angles of obstacles

定义2：以SE为基准线，S为支点，分别向障碍物块的两侧移动，形成夹角∠iOSE即为障碍物映射角。

随着地图中障碍物数量的增加，需要计算映射角的障碍栅格点变得越来越多，使得算法计算量增大，效率降低。为了避免出现这种问题，本文依据起点S与障碍物块的位置关系仅选取某一方向上的边缘障碍物栅格点，可大幅降低待计算结点数量。以图5为例，起点位于障碍物块的X轴负方向以及Y轴正方向，因而只选取障碍物块X负方向的边缘点与Y正方向的边缘点即可，则待计算的障碍栅格点为 O1、O2、 O3、 O4、 O5、 O6、 O7、 O8、 O9、O10，在此方向上计算障碍物映射角，可有效节约系统资源，保证算法的高效性。具体操作步骤如下：

Step1：检测起点S与障碍物块的相对位置，并选取此方向上的障碍物块边缘栅格点组成集合G，计算G中所有栅格点的映射角；

Step2：依据障碍物边缘栅格点与起点、终点连线的左右位置关系，将G中所有栅格点分为两类，记作集合 GL与GR；

Step3：若 GL中最大的障碍物映射角唯一，则对应栅格为左登陆点，若 GR中最大的障碍物映射角唯一，则对应栅格为右登陆点，程序结束；若不唯一，进入下一步；

Step4：删除 GL与GR中非最大映射角的栅格点，分别计算 GL与GR中所有栅格点到起点S的直线距离，距离最短者即为登陆点。

1.5 扩展登陆点

无障碍物阻挡时，直线是两点之间最短路径；受到障碍物阻挡时，最短路径转折点一定位于障碍物边缘附近，如将登陆点向邻近的非障碍栅格扩展，则能够覆盖最短路径转折点。以8邻域为例，在每一个登陆点8邻域内进行扩展，找到所有自由栅格点，作为路径规划的搜索空间。

如图6所示，栅格点O是障碍物块BLOCK的一个登陆点，在其8邻域范围内进行扩展，扩展出7个自由栅格点OE1、OE2、OE3、OE4、OE5、OE6、OE7。依此类推，对地图中所有登陆点进行扩展，扩展出的栅格点组成了路径规划搜索空间，从而实现地图规模的有效缩减，然后利用搜索空间中的栅格点构建赋权图，以图7为例，赋权图由起点、终点以及所有黄色结点与红色边组成。

图6 8邻域登陆点扩展Fig.6 Landing node expansion in 8 neighborhoods

图7 非负赋权图Fig.7 Non-negative graph with weight

2 改进Dijkstra算法

Dijkstra是一种很有代表性的最短路径算法，它是计算机科学家Edsger W. Dijkstra于1956年提出的，可用于搜索非负赋权图的单源最短路径。Dijkstra算法要求每条边都有一个非负的代价值，算法从起点开始，遍历图中每一个结点，它从未遍历的结点集中选取与当前结点最近的结点进行扩展，当搜索到目标结点时结束，该算法逻辑简单，搜索速度快，常作为其他图算法的子模块使用，图8是Dijkstra算法流程图。

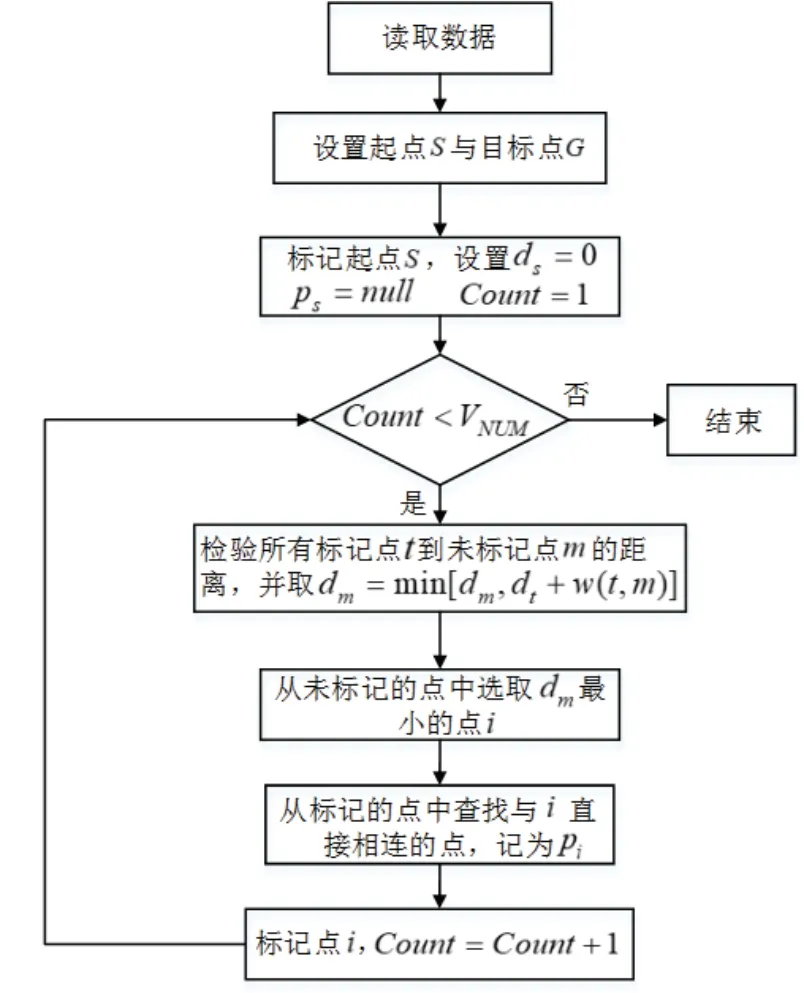
图8 Dijkstra算法流程图Fig.8 Flow chart of Dijkstra algorithm

其中， pi表示从起点S到结点i的最短路径中，i点的前一个结点；dt表示从起点S到结点t的最短路径长度，Count是初始值为1的计数器，VNUM为图的顶点数量，w(t,m)表示从结点t到结点m的路径长度。

Dijkstra从起点出发，搜索最近结点并逐步向外扩展，在机器人路径规划问题中，终点往往是距离起点最远的结点，当结点规模较大时，利用Dijkstra算法寻找最短路径效率太低，于是结合赋权图结构特点对Dijkstra算法进行改进，进一步提高本文算法的路径规划效率。为更好地展示赋权图特点，将图7转换为图9，由于图9中结点为平面坐标点，各结点间代价均为坐标点的直线距离，因而符合“三角形两边之和大于第三边”定理，例如 SN1＜ SN15+ N15N1，则图中结点N15非最短路径覆盖点；同理，N3N10＜ N3N25+ N25N10，N3N10＜ N3N16+ N16N10，则结点N25与N16非最短路径覆盖点。以此类推，图9中只有结点 N1、N2、N3、N4、N5、N6、N7、N8、N9、N10、N11、N12可能位于最短路径之上，其余结点与最短路径无关且会增加算法计算量，于是对Dijkstra算法进行改进，详细描述如下：

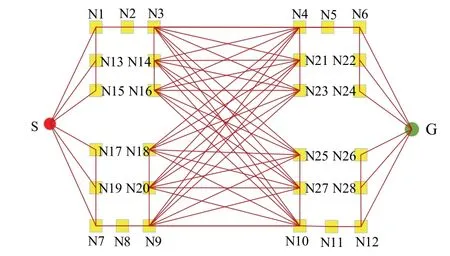
图9 非负赋权图结构Fig.9 The structure of non-negative graph with weight

Step1：初始化赋权图结点集合U ={S, N1, N2...Nn-2,G}，集合T=∅ ，V=∅ ，W = {q|q ∈ U 且q∉ V}，结点P=S；

Step2：利用碰撞检测法检测结点P与W中每个结点是否可直达，如可直达，则将W中对应结点插入集合T；

Step3：比较T中每个结点的障碍物映射角，如小于对应登陆点映射角，则从T中删除该结点，同时删除U中该结点；如大于或等于登陆点映射角，则保留；

Step4：计算结点P到集合T中所有结点之间的代价

St ep5：计算dS,Tk=dP,Tk=|P-Tk|，同时将P结点加入集合V进行标记；，令P=Tk，T=∅。如P是终点G，则算法结束；否则进入Step2。

其中：Tk是集合T中第k个结点，dP,Tk是结点P到Tk的直线距离，n为赋权图中所有结点的个数。

3 实验分析

通过对比实验观察不同算法的路径规划效果。在Windows 10平台上利用C#语言开发一套算法实验平台，如图10所示。

图10 算法实验平台Fig.10 Algorithms experiment platform

以路径长度和运行时间作为评价指标，分别在四组100×100的栅格地图中进行实验，实验环境选取随机障碍物分布地图2组、办公室走廊区域地图1组以及实验室内部地图1组，通过与传统A*算法以及JPS算法进行对比，分析本文算法的优劣。各算法实验效果如图11所示，其中黑色圆形结点为起点，黑色三角形结点为终点，黑色栅格为障碍物，浅绿色栅格为A*或JPS算法的扩展结点，红色栅格为本文算法的扩展结点，红色折线为最优路径。将三种算法的路径规划数据汇总到表1可知，A*算法与JPS算法路径规划距离相同，而本文算法规划距离略短，表2对路径长度进行了对比，显示本文算法比A*算法的路径长度缩短了大约2~5个百分点，这是由于本文算法将扩展结点的连线作为最优路径的一部分，打破了传统N邻域扩展的角度限制，可规划任意角度，因而规划路径的转折次数更少，路径更短。表3对三种算法的运行时间进行了比较，可以看到新算法的搜索效率比传统A*算法有了大幅提升，耗时约为传统A*算法的5%~25%，效率提升幅度随着扩展结点数量的变化而变化。同时，本文算法与JPS算法相比，路径规划效率也有提升，在地图M1、M2和M4中，两种算法的扩展结点数量相当，耗时比值约为94%~100%，算法效率提升不明显，而在地图M3中，办公室走廊区域的障碍物分布集中，所有障碍栅格点共同组成了一个障碍物块，使得本文算法扩展结点数量较少，而JPS算法在障碍物拐点处扩展结点较多，计算冗余结点耗费了更多时间，因而本文算法耗时仅为JPS算法的27.02%，优势明显。通过以上数据可知，本文算法更适用于障碍栅格点集中或障碍物块数量较少的大规模地图中。

表1 三种算法运行结果Tab.1 Running results of three algorithms

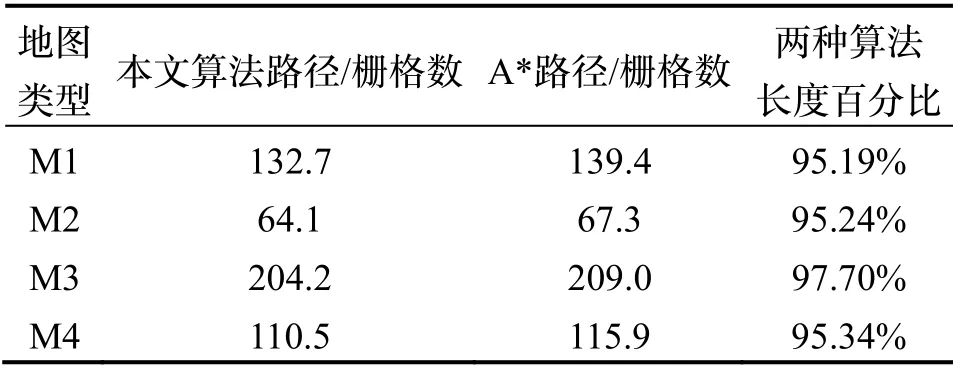
表2 路径长度对比Tab.2 Comparison of path length

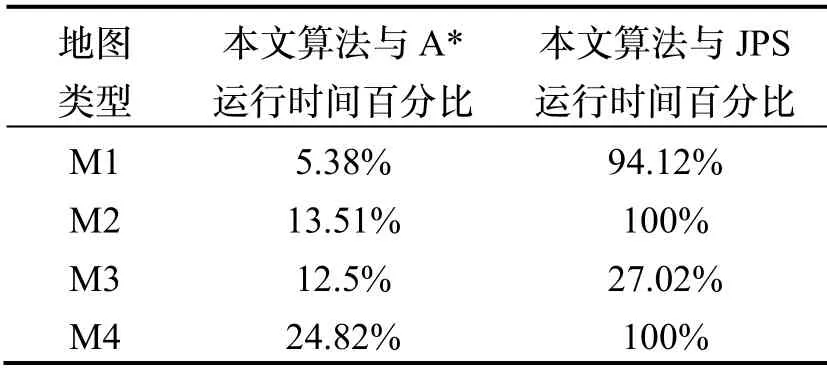
表3 运行时间对比Tab.3 Comparison of running time

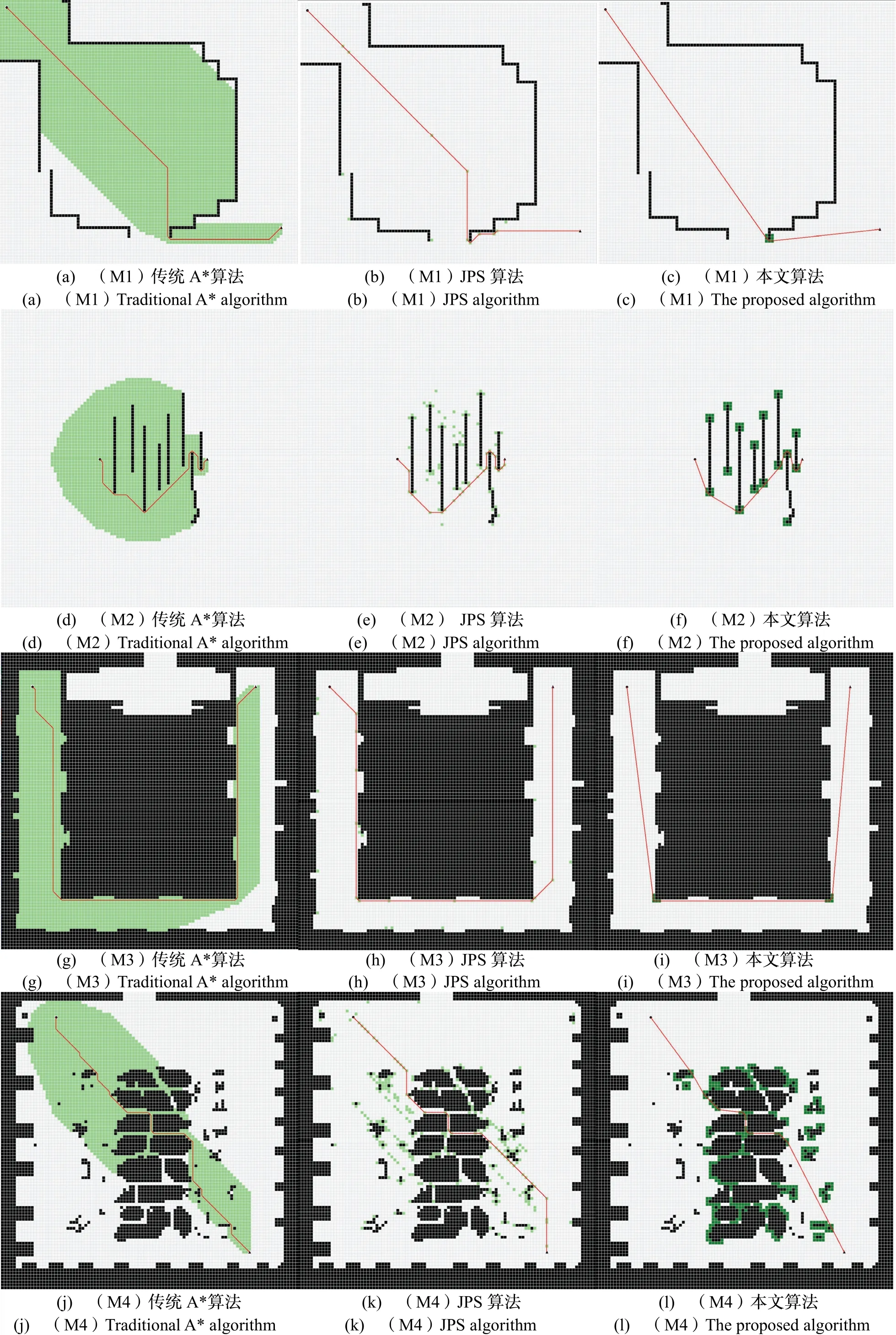
图11 路径规划结果Fig.11 Results of path planning

4 结 论

在移动机器人路径规划过程中，计算时间受到地图规模的影响较大，实时性问题突出。为解决这一问题，本文提出了一种基于障碍物登陆点检测的全局路径规划算法，利用障碍物在地图中的整体分布信息，通过计算映射角寻找障碍物登陆点，锁定相关障碍物的边缘区域，有效缩小地图搜索范围，再通过改进Dijkstra算法优化最短路径搜索过程。最后，以A*算法与JPS算法作为参照进行实验，实验结果表明，本文所提算法可有效提高路径规划效率，尤其是在障碍物比较集中或障碍物块数量较少的大规模地图中，能更好地解决实时性问题。但机器人不是一个质点，运行路线还需考虑其实际尺寸，下一步还要对路径安全性做进一步的优化。