强噪声下全驱空中作业平台自抗扰反演控制

马 乐，刘 杰，马志丽，闫一鸣，徐东甫

（1. 东北电力大学 自动化工程学院，吉林 132000; 2. 渤海船舶职业学院 电气工程系 葫芦岛 125105）

目前建筑物外观清洁、输电线装配、光伏设备维护等绝大部分空中作业仍依赖人工，其风险性、艰巨性与低效性显然。行业需要、人本诉求，使研制有效的空中自动化作业设备成为产业升级的必然趋势。

旋翼飞行平台与机械臂结合的空中作业系统（Aerial Manipulation System, AMS）弥补了传统旋翼无人机执行能力不足，同时继承了传统旋翼灵活机动、操作简单、对复杂环境的高度适应等优点[1,2]，能灵活地实现广泛的主动空中作业任务（如图1）。有效的AMS能显著提升空中作业自动化水平，为开辟新产业空间和经济链提供良好契机。因此近年AMS研究受到广泛关注[3]。

图1 空中作业机器人操作示意图Fig.1 Diagram of application scenarios of aerial manipulation

现有研究几乎涵盖了各类传统飞行平台与不同类型操作机构的结合方式。多旋翼与串联机械臂的结合方式在灵活性、可控性等方面较其他结合方式有显著优势[4,5]。飞行平台运动相对局限，因此Euler角被广泛采用以分析飞行平台运动学，机械臂运动则以Denavit-Hartenberg（D-H）方法为主。动力学建模则继续沿用旋翼平台与机械臂领域的Newton-Euler和Lagrangian分析方法[6,7]。

虽然AMS研究取得了一系列成果，但因其系统复杂性导致现有研究成果不足以支撑实际作业任务[8]。其中飞行平台控制是关键问题之一[9]，其难点在于：1）AMS属一类树形无根多刚体系统，其强耦合与非线性增加了控制难度；2）飞行平台与机械臂间存在动态约束，机械臂的位形与速度影响平台控制，平台运动又决定机械臂末端执行器位姿；3）目前采用飞行平台多为非完整结构，位置与姿态控制需分部控制，在控制中势必牺牲位置或姿态精度；4）姿态控制是飞行平台控制的核心，采用惯性测量技术的传感器在测量时不可避免会产生噪声，对控制的精度产生一定程度的影响；5）由于机构限制平台无法对机械臂运动提供足够的补偿，进而影响系统稳定性。因此AMS飞行平台控制问题亟待解决。

为增强稳定性，文献[10]采用减小机械臂体积以此减小因后者运动造成的影响，但该方式导致了系统负载能力较低。文献[11]集成了大功率机械臂以提升负载能力，但该方案将研究重心放在机械臂的规划，增加了复杂度，同时因设备庞大不适用于常规空中作业任务。文献[12]采用多个旋翼平台共同搭载同一机械臂以提升执行能力并降低机械臂对单个旋翼平台影响，然而该方式增大了系统的运行空间并提升了系统协同难度，影响稳定性。

除机械参数外，子系统间作用对平台稳定性也至关重要。文献[13]发展了上述研究，视AMS为整体时变刚体，通过估计机械臂运动时AMS整体质心与惯性张量设计控制器。但该方法在动量定理中的理论依据与精度有待讨论，且从算法过程看出计算动态惯性张量与质心位置本身难度巨大，仅当机械臂低速且空载运动条件下才近似接近实际状态。

文献[11-13]等视子系统间作用力/矩为扰动并依此设计控制器，但当作用力/矩持续变化时该方法控制效果欠佳。文献[14]采用模型预测控制以调和上述扰动，但控制性能受目标函数设计影响，同时解算相对复杂影响实时性。文献[15]建立了系统间作用力/矩解析表示，由此可分析并设计动态负载补偿项。但现有飞行平台因机构局限，无法对任意方向的动态负载力/矩给予充分补偿。

同时，由于惯性传感器的信号中存在随机的非高斯噪声[16]，不准确的噪声信息可能导致位置和速度漂移。并且噪声的大小可能会在不同的应用和环境中发生变化。这意味着在实际应用过程中噪声具有时变性，因此传感器的噪声问题是飞行平台控制的重要问题。文献[17]中针对飞行平台能力的限制，无法使用大体积、重质量的惯性测量单元，提出了一种变距离多普勒质心的误差估计方法，以提高惯性系统的精度。文献[18]针对磁干扰影响多旋翼航向出现偏差问题，提出基于扩展Kalman滤波的姿态信息融合方法，通过建立可调节测量噪声方差矩阵，实现自适应修正多旋翼飞行器航向功能。

上述分析得出有效的AMS飞行平台设计与控制仍为亟待解决问题。文献[19]打破了传统多旋翼结构，通过调整旋翼位置与方向等参数设计出具有全向驱动能力的飞行平台。基于全向驱动设计思路，作者前期设计了一种基于全向驱动旋翼平台的空中作业系统及其PID控制方法[20]。

为进一步提升控制性能，本文在前期工作[20]基础上提出了一种基于自抗扰、反演与动态补偿的全驱空中作业飞行平台控制方法，记为ABC（Adrc,Backstepping, Compensation）控制。针对空中作业机器人动力学模型较为复杂问题，采用Carig与递归Newton-Euler方程推导了有效的动力学模型。考虑机械臂对飞行平台产生的扰动影响，建立了飞行平台全向驱动控制补偿项，并结合自抗扰控制技术、反演控制技术以及动态补偿策略，有效地解决了强噪声、干扰和不确定性问题，提升了控制性能。

1 全驱AMS机械结构

图2 为全驱空中作业系统SolidWorks设计图。与传统平台不同，本文旋翼结构为大倾角( βi＜ 60°)，因此旋翼能够提供机体坐标系x与y方向的推进力以及力矩，进而能实现飞行平台的全向驱动。

图2 全向驱动AM系统SolidWorks结构图Fig.2 Structure chart fully-actuated AM system in SolidWorks

系统机械臂设计为4关节以兼顾灵活性与负载能力。采用Dynamixel AX-12A伺服舵机为关节驱动，该舵机具有位置、速度等反馈功能，结合电压、电流、负载等反馈信息可估计关节角加速度，并能以位置、速度作为指令控制关节运动。

2 系统建模

设惯性参考坐标系、旋翼平台坐标系和机械臂第i关节坐标系分别为｛W ｝、｛A｝、｛ Mi｝，｛A｝相对｛W｝位姿矩阵为：

其中0PA与0RA分别为｛A｝相对｛W ｝的原点向量与旋转矩阵，0RA可由 x,y,z向欧拉角[φ,ψ,γ]得到。

机械臂关节坐标系i-1与i间变换矩阵表示为（规定i=1为关节1与｛A｝变换矩阵）：

其中i-1Ri为i系到i-1系旋转矩阵，i-1Pi为i系原点在i-1系坐标。采用Craig参数计算i-1Ai。其中为常数，θ为关节角度变量。表1为本文机械臂Craig配置参数表（为方便表示末端执行器位姿，加设虚拟关节5）。

表1 机械臂Craig参数表Tab.1 Craig parameters list of manipulator

由坐标系传递关系，可得各关节坐标系相对｛W ｝系位姿矩阵：

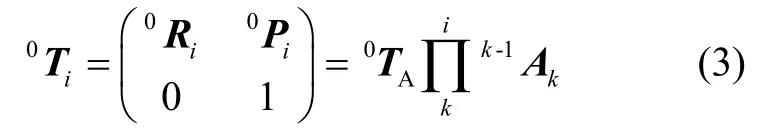
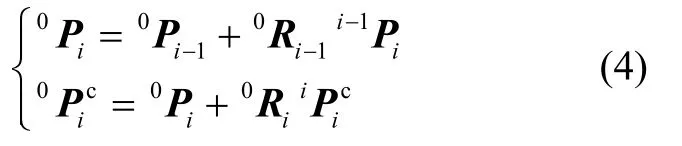
飞行平台角速度0ωA与[φ,ψ,γ]导数关系为：

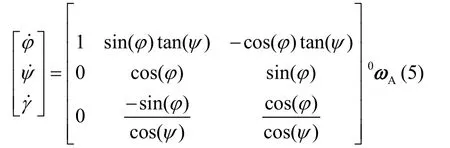
各关节坐标系角速度由0ωA与关节角速度决定，并有递推关系：

Z0=［ 0,0,1］T。

对式(4)求导得关节坐标系间线速度关系如下：

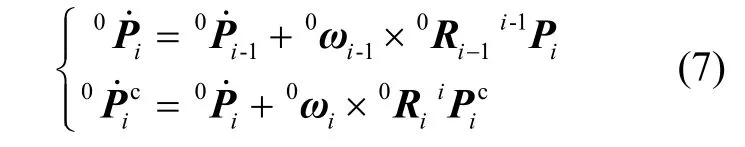
式(1)-(7)建立了飞行平台与机械臂各连杆坐标系位置、姿态与其角速度关系。

采用递归Newton-Euler方程建立系统动力学模型，变量均为｛W ｝系下表示。旋翼平台的动力学方程如下：

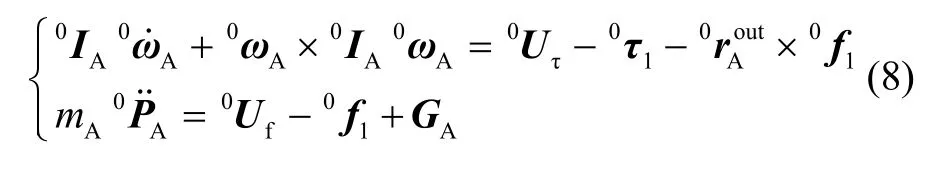
其中0Uf、0Uτ分别为旋翼产生的驱动力/矩，0f1与0τ1分别为旋翼平台对连杆1的力/矩，作用在连杆1的力臂向量，mA与0IA分别为旋翼平台质量和相对｛W｝的惯性张量，GA为旋翼平台重力向量。

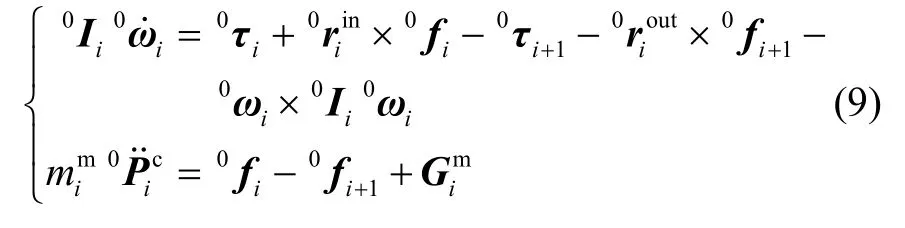
其中0fi、0τi分别为连杆 i- 1对连杆i的力/矩，mi与0Ii分别为连杆质量和相对｛W ｝的惯性张量，为连杆i重力向量。分别为连杆i-1、i对连杆i、 i+1的力臂向量：

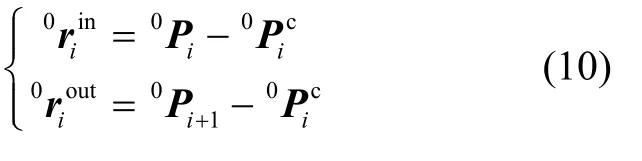
对式(6)(7)求导得：

联立式(8)-(11)构成二阶代数微分方程组，并视二阶项为变量，其他参数为常量，求解方程。

3 自抗扰-反演动态补偿控制

从前节分析看出旋翼平台动力学模型呈多输入多输出（Multiple Input Multiple Output, MIMO）二阶非线性，且与机械臂系统存在强耦合。相比传统多旋翼平台，AMS旋翼平台稳定性受机械臂严重影响。为此本文利用动力学模型特性建立动态补偿项以抵消机械臂对平台影响，并分别基于自抗扰与反演控制设计平台位置与姿态控制器。

3.1 动态负载补偿

分析式(8)得出，平台质心加速度与角加速度除受驱动力/矩控制外还与角速度、机械臂作用力/矩有关。视机械臂作用力/矩为平台负载项，并依此建立补偿项udc以抵消其作用：

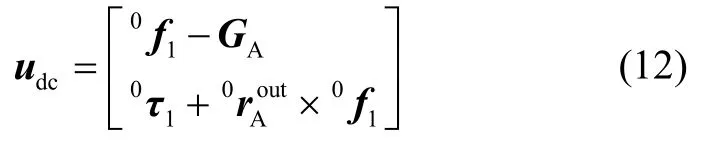
通过求解(8)-(11)联立的方程组得到补偿项所需参数，详见作者前期工作[20]。控制输入引入该补偿项能化简平台动力学模型，从而将AMS平台控制问题转化为传统多旋翼控制问题。控制器输入形式为：

其中uap为旋翼平台控制器输入。考虑对平台位置的扰动与姿态稳定性，本文分别采用自抗扰与反演控制分别设计平台位置与姿态控制器。

3.2 平台位置自抗扰控制

设飞行平台位置 PA与速度为系统状态消除补偿项后式(8)位置部分化简为：

式(14)为MIMO二阶系统，下面设计其ADRC控制器。ADRC控制器由基于微分跟踪器（Tacking Differentiator, TD）的过渡过程、扩张状态观测器（Extended State Observer, ESO）与非线性反馈控制律组成。

二阶非线性最速TD的离散形式表示为：

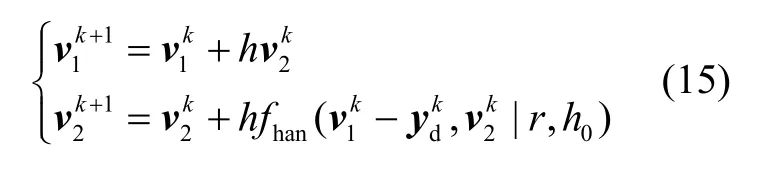
其中h为采样时间，yd为控制期望，1v与v2分别为过渡过程输入及其跟踪微分信号，fhan为特殊函数：

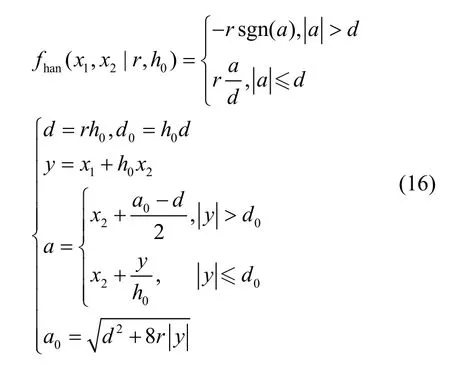
ESO以系统输出观测量yh估计系统状态，二阶离散形式为：

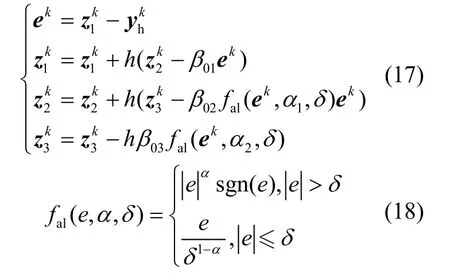
其中β、α、δ为可调参数。

以非线性状态误差反馈作为ADRC控制输出，本文采用形式为：

其中b0、与 δu为可调参数，二阶系统中N=2。

3.3 平台姿态反演控制

考虑二阶MIMO系统：

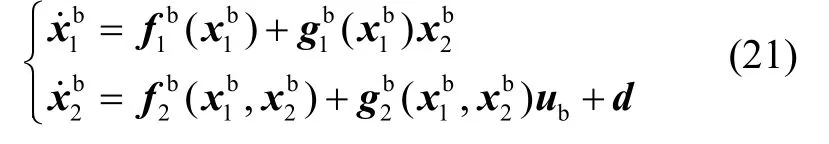
设计其反演控制器，首先定义误差系统：

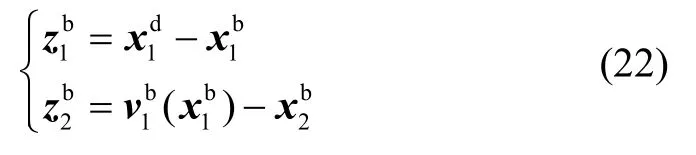
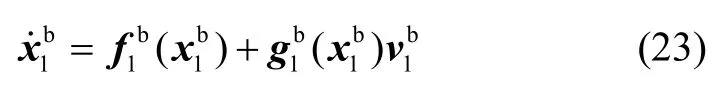
选择Lyapunov函数：

式(22)(24)对时间求导并将式(23)代入得：

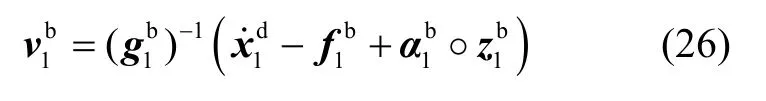
取

则式(31)为：

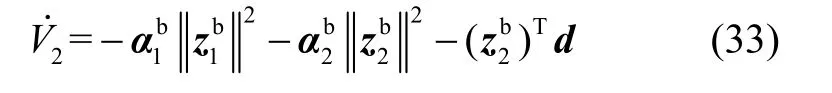
利用Yong不等式：

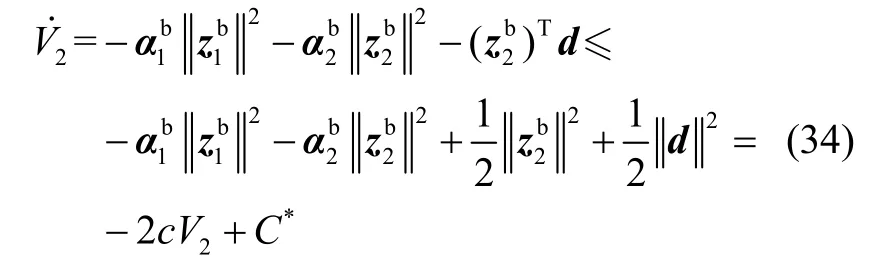
其中J由式(5)得到，I3×3为3维单位矩阵，则式(8)姿态部分化为式(21)。因此可由式(32)得到旋翼平台姿态控制律。

4 仿真分析

4.1 仿真系统描述

为提高仿真运行效率并避免版权问题，本文仿真系统从前期的Matlab实现转为基于Python的开源项目集，涉及主要模块如表2。（注：因项目处于过渡时期，本文仿真程序与数据处理部分依赖Matlab）

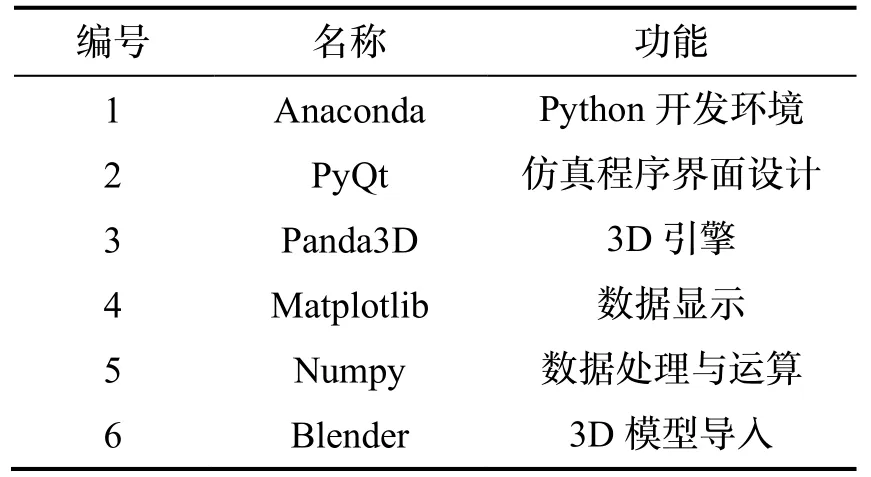
表2 仿真系统主要模块说明Tab.2 Main module of the simulation system

4.2 全驱控制测试

本节测试所提出的方法在全驱控制问题中的性能。选择四种具有代表性的机械臂静态位形分别为[-90°, -90°, 0°, 0°]、[- 90°, 0°, 0°,0°]、[ 0 °,0 °, -90°,0°]与[- 90 °, 0 °, - 90 °, 0°]。首先测试AMS的全驱位置控制，令初值位置为 [9m, 9m, 9m]，期望位置为[10m, 10m, 10m]，初值与期望 Euler角均为[0 °,0°,0°]。仿真参考模型参数不确定性为±10%，相对前期工作仿真增大噪声幅值分别为± 30 mm与± 3 °范围的高斯分布，施加± 10 N与± 80N·S范围的高斯分布扰动，扰动间隔时间为1 s，控制频率为100 Hz。

图3 为基于本文方法的四种机械臂位形下旋翼平台全驱位置控制误差曲线图，从中分析出：1）旋翼平台在四种位形并伴随噪、扰条件下均能在X,Y,Z三方向约2秒内无超调收敛至期望，同时位移误差曲线相对平滑，其原因为ADRC中TD起了去噪作用；2）在控制过程中平台三个姿态角误差始终在± 2 °内，该误差小于仿真传感器噪声，因此设计的反演姿态控制器能在位移控制中以很小误差保持姿态稳定。综上，在不同静态机械臂位形与噪、扰条件下，本文方法在不牺牲姿态前提下同时实现三维位置全向驱动控制。

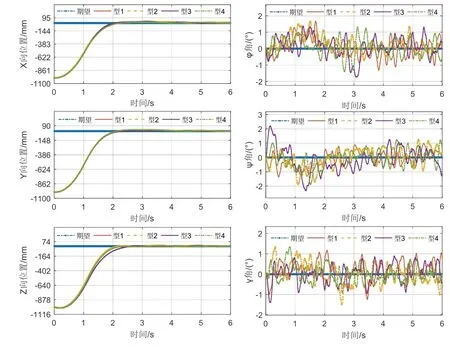
图3 四种机械臂位形全驱位置控制误差曲线Fig.3 Errors of control in 4 types of configurations of arm

设机械臂位形为[-90 °, -90 °, 0 °, 0 °]，以上述仿真扰动为单位施加1-5倍扰动，测试本文方法在有倾角悬停控制中性能，初始与期望位置均为 [9m, 9m, 9m]，初始Euler角为[0 °, 0 °, 0 °]，期望为[20 °, 20 °, 0 °]，其余仿真参数同上。

图4 为上述条件下有倾角悬停控制位姿响应曲线，从中分析出：1）φ与ψ姿态角均能快速收敛（调节时间＜1 s）至期望；2）不同扰动等级下Euler角均能以较小误差（±1.5 °）保持稳态；3）X与Y方向均能以小误差稳定在期望位置，但由于阶跃响应、随机扰动冲击、系统旋翼动力参数限制与重力约束，Z方向在初始时刻产生向下震荡，最大幅度为48 mm，然而能在1.5秒内实现稳定调节，并保持低误差稳定。综上得，本文方法在有倾角悬停全驱控制中响应速度快、误差低，对噪声与扰动具有较好抑制能力。

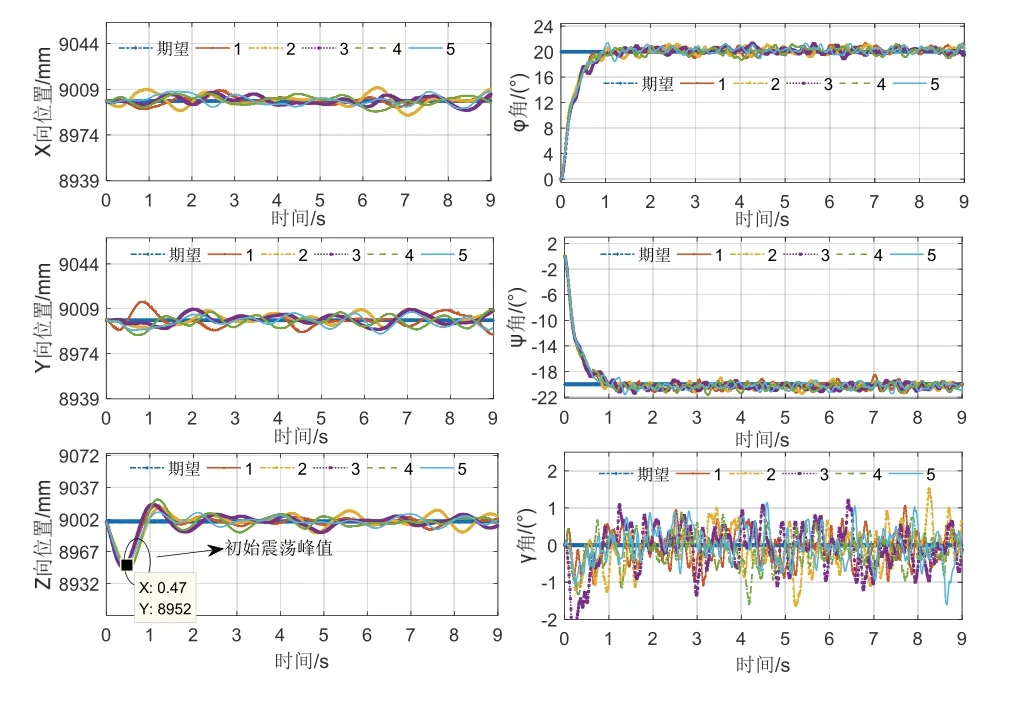
图4 不同等级扰动下倾斜悬停控制响应曲线Fig.4 Response curves of tilted hover control under different levels of disturbance

4.3 空中作业任务仿真

实际空中作业势必需要机械臂的运动，为此本文模拟两类空中作业任务，并与前期工作[20]中方法比较，分析本文方法在伴随机械臂运动的空中作业任务中性能。相对文献[20]中设置提高扰动范围至± 40 N与± 300 N·S。

任务1为机械臂运动下的悬停控制，机械臂初始关节角度为[-90 °, 0 °, -45 °, 0 °]，初始与期望Euler角均为0 °，关节3以=0.5sint 速度运动，噪声与模型参数不确定范围同上。

图5 为本文方法（ABC）与文献[20]方法（DC-PID）任务1的位置与姿态误差曲线，从中分析出：1）X与Y方向两方法控制效果基本相同，均能以较小误差（±15 mm内）保持稳定；2）由于系统功率限制、初始扰动与重力约束两方法在-Z方向均产生震荡，文献[20]方法随后出现了一定程度稳态误差（约为20 mm），但本文方法仍能在1秒内完成调节并以小误差稳定，该结论与前节仿真结果一致；3）两方法对于γ角均能以± 1.5 °误差范围保持稳定，但文献[20]方法因机械臂运动与较大扰动因素在初始时刻在φ与ψ角较本文方法出现明显震荡。综上得出，两方法针对任务1问题均能实现稳定控制，但本文方法在大扰动条件下具有更好的抗扰能力与动态性能。

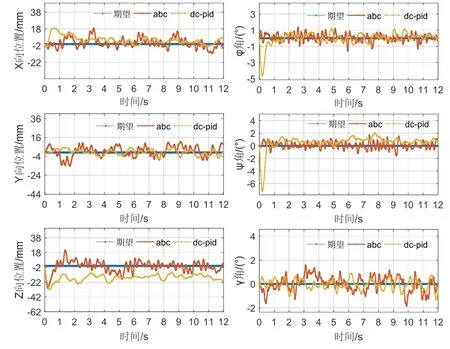
图5 任务1位姿误差曲线Fig.5 Errors of positions and attitudes for task 1

在上述条件基础上，任务2加入平台的全驱运动，设初始与期望位置分别为[9 m, 9 m, 9 m]与[10 m,10 m,10 m]，其余参数同任务1。

图6 为两种方法任务2条件下位置与姿态误差曲线，从中分析出：1）本文方法在X与Y方向的调节时间较快，在Z方向的响应速度本文方法优势更加明显；2）与任务1相似，本文方法在φ与ψ角调节初期震荡明显小于文献[20]方法；3）由于比任务1增加了条件及系统性能限制，本方法γ角调节初期存在相对前一任务较大震荡，但能在较短时间实现校正，其稳态误差与文献[20]方法相当。综上得出，本文提出方法在任务2条件下综合性能优于文献[20]方法。

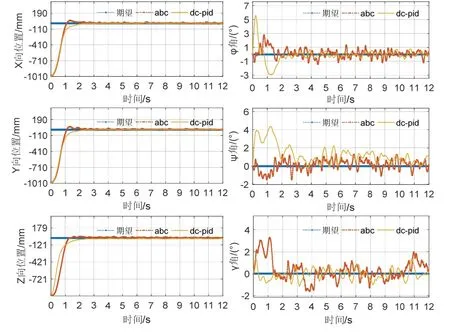
图6 任务2位姿误差曲线Fig.6 Errors of positions and attitudes for task 2

上述仿真分析得出，本文方法较前期提出方法具有更好的扰动抑制能力与稳定性，从而在更大的噪声与扰动条件下具有更好的控制性能。

4.4 CoppeliaSim平台仿真实验

利用Coppeliasim物理仿真系统搭建了虚拟实验平台，如图7所示。

图7 CoppeliaSim虚拟实验仿真平台Fig.7 The demonstration of virtual experiment in CoppeliaSim

本文的仿真控制周期为0.01 s。物理引擎选择Bullet 2.78。将精度设置为最高精度。在前面数值模拟的基础上，着重在实际问题中验证该方法的有效性。初始位置为 [2m, 2m, 2m]。期望位置为 [3m, 3m, 3m]。初始值和期望欧拉角为[0 °, 0 °, 0 °]。第三关节以θ3= 0.5sint的速度从-π3向π3周期性摆动。噪声和模型参数不确定性的范围与上述相同。

图8 为ABC控制方法和文献[20]所述的DC-PID方法在相同条件下产生的位置和姿态响应曲线。从图8可以看出，两种方法都能在X,Y,Z方向收敛到期望信号，而ABC方法在3秒左右收敛到期望信号。另一方面，DC-PID收敛到需要的信号需要4-6秒。由此可以看出，ABC方法具有更快的响应速度。在这两种方法中，由于在本节中测试的机械臂负载，φ的角度出现了一定程度的震荡。由于关节3的连续运动，力会不断地传递到飞行平台上。在这种连续的强扰动作用下，ABC法的振荡范围更小。图9与图10为两种方法的位置跟踪和姿态跟踪平均跟踪误差绝对值对比柱状图，从图中可看出，无论是位置跟踪还是姿态跟踪，本文方法的平均跟踪误差绝对值都小于DC-PID方法。相比于DC-PID方法，本文方法的平均跟踪误差绝对值在位置X,Y,Z方向的跟踪控制中分别降低了37.9%、45.9%、64.2%，在姿态φ,ψ,γEuler角跟踪控制中分别降低了73.2%、84.6%、78.8%。即本文方法相比DC-PID方法，在位置与姿态跟踪控制中，平均跟踪误差绝对值降低37.9%~84.6%。综上所述，两种方法均能实现稳定控制，但ABC法具有较好的抗扰动能力和较强扰动条件下的动态性能。

图8 CoppeliaSim实验位姿响应曲线Fig.8 Responses of positions and attitudes for CoppeliaSim

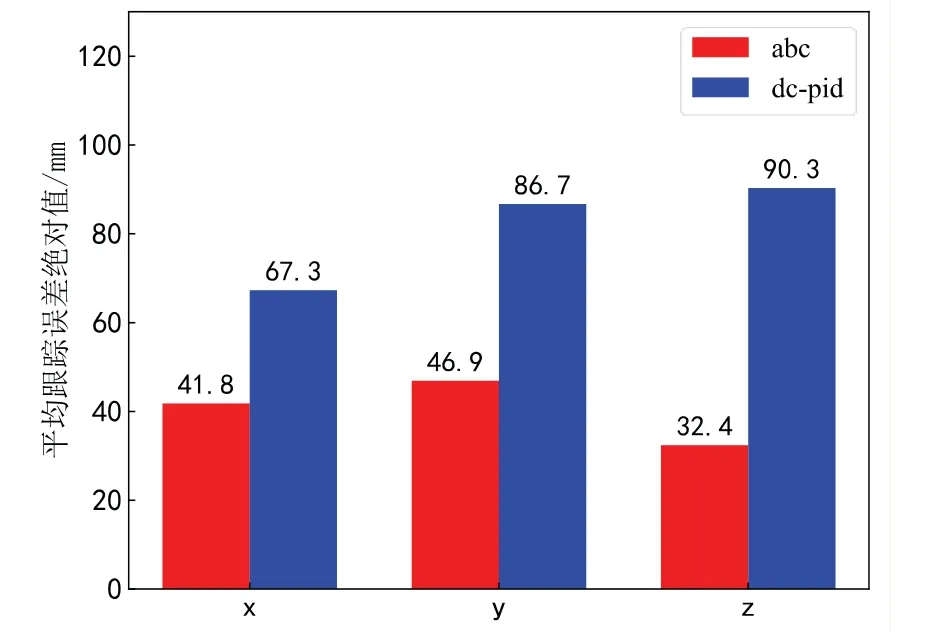
图9 位置系统跟踪误差Fig.9 The position system tracking error

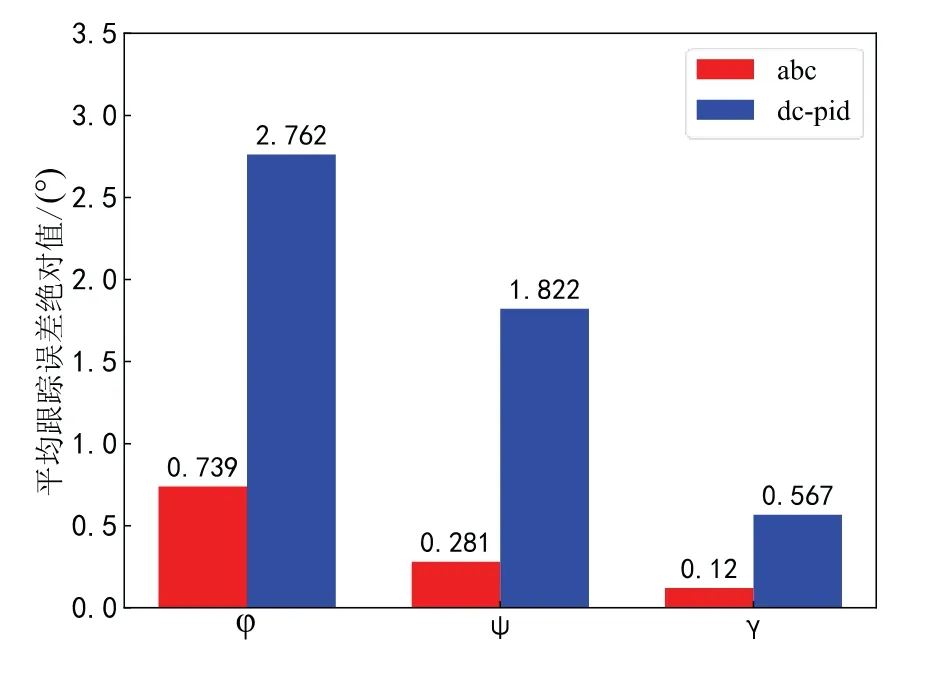
图10 姿态系统跟踪误差Fig.10 The attitude system tracking error

5 结 论

通过上述论述与分析得出如下结论：1）提出的基于模型动力学的补偿项能够化简系统并抵消机械臂对系统作用影响；2）相比前期DC-PID方法，本文提出的自抗扰反演控制在强噪声、扰动条件下具有更好的控制性能。

未来将在优化系统机构设计、建立柔性学习控制、建立实时解耦方法等方面开展进一步工作。