基于微分包含镇定的固体运载火箭上升段轨迹跟踪

刘 飞，王松艳，杨 明，晁 涛

（哈尔滨工业大学 控制与仿真中心，哈尔滨 150080）

固体运载火箭（Solid Launched Vehicles，SLV）上升段制导一直是备受国内外学者关注的研究方向。基于极大值原理的间接法在理论上可以保证轨迹的最优性[1]，然而该方法对于协状态量初值的选取较为敏感，且由最优条件构成的约束方程较为复杂。相比之下，基于凸优化的直接法可以较大程度地提高计算效率，因而广泛应用于上升段轨迹优化[2]。然而，多数约束无法无损凸化，且模型不确定性对制导精度影响较大。对于实际飞行中存在不确定性的情况，一般在标称情况下采取直接法或间接法离线获得最优参考轨迹，然后设计轨迹跟踪制导律，导引SLV沿参考轨迹运动。

对于参数时变、强非线性的SLV上升段，若采用基于时不变模型的控制器[3]，其跟踪精度可能相对较低。基于改进PID[4]的轨迹跟踪方法需要在飞行包络线内设计多个控制器，这无疑增加了控制器设计的工作量，且控制器间的切换处理增加了设计难度。基于LQR[5]的跟踪方法中，权重矩阵Q和R的选取对闭环系统的性能有明显的影响，其选取原则很大程度依赖设计人员的经验。基于动态逆[6]的轨迹跟踪方法虽然避免了上述问题，但对模型精度要求较高。若用于参数摄动下的轨迹跟踪问题时，可能需要与其他方法相结合。基于变结构控制[7]的轨迹跟踪方法鲁棒性较强，但控制器往往包含较多的设计变量，具有一定的设计难度，且可能造成控制量抖振。文献[8]提出了一种适用于SLV的自适应最优轨迹跟踪控制器，对初始状态偏差和气动不确定性具有良好的抑制效果。该方法在发动机比冲和秒流量摄动下的鲁棒性能还有待进一步研究。近些年来，基于扩张状态观测器的估计-补偿跟踪方法在工程实践中得到了广泛应用[9]。文献[10]针对轨迹跟踪问题，设计了有限时间扩张状态观测器（Extended State Observer, ESO），实现了对不确定性的实时观测与补偿，提高了制导系统的鲁棒性。然而，固定参数的ESO无法保证在大范围参数摄动下，依然具有良好的观测效果。文献[11]提出了一种基于双曲正切函数的变参数ESO，其结构较为复杂，是否适用于快时变、强非线性的SLV上升段还有待商榷。

另一个思路是将不确定性和动力学系统作为一个整体，扩展为微分包含系统。微分包含系统是在对系统过程有一定了解的但不完全确定的基础上建立起来的动态系统，是描述不连续或不确定动力系统的重要方法，也是微分方程的推广[12]。根据微分包含系统的原理，如果某一微分包含系统可被镇定，那么它所包含的任意子集均可被镇定[13]。除一般控制问题外，混合模型系统和不确定参数系统也可视为微分包含系统[14]。在文献[15]中，利用凸胞Lyapunov函数构造了一类非线性微分包含系统的非线性反馈律。文献[16]采用滑模控制方法研究了多胞体微分包含系统的稳定性。

基于以上分析，本文引入微分包含的思想，将上升轨迹跟踪问题转化为微分包含系统的镇定问题，以达到适用于大范围不确定性的目的。本文主要工作包括：

1) 将考虑发动机比冲量、秒流量和气动系数不确定性的状态偏差系统描述为上升段微分包含系统，将轨迹跟踪问题转化为微分包含系统的镇定问题。

2) 提出一种适用于上升段微分包含系统的镇定控制器。证明了当参数不确定性在给定的边界值之内时，在控制器的作用下，状态偏差收敛至有界范围。在发动机比冲、秒流量和气动系数大范围不确定性的情况下，实现了对参考轨迹的精确跟踪。

3) 为了避免在实际飞行过程中违反过载约束，考虑了攻角和侧滑角修正量的幅值饱和约束，将该约束转化为线性矩阵不等式进行求解。

1 上升段微分包含模型建立

为了简化计算，对模型进行如下假设：1)将SLV视为质点，忽略转动；2)不考虑摆动喷管的影响；3)将地球视为球体；4)上升飞行时间短，忽略地球自转引起的离心力和科氏力。考虑SLV受到的推力、气动力和重力，在轨迹坐标下建立上升段运动方程如下：

其中，v为速度，h为高度，Θ为当地弹道倾角；α和β分别为攻角和侧滑角；σ为当地弹道偏角；Pe和m分别表示发动机推力大小和SLV质量；g为重力加速度。气动力大小的计算方式如下：

其中，cx和cy分别为阻力系数和升力系数；ρ为大气密度；Sm为气动有效面积。

在实际飞行中，由于发动机工作环境不同（如温度、装药质量、加工误差等），发动机的比冲和秒流量与地面试验结果不同：

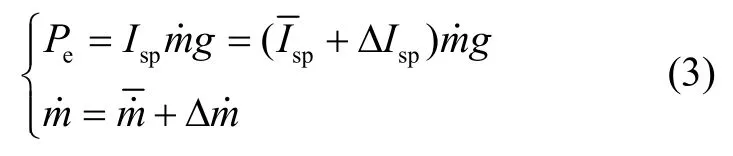
另一方面，理论计算的局限性以及风洞实验与实际飞行条件的差异导致了实际气动特性存在误差：

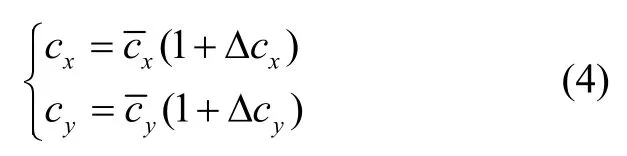
将上升段非线性系统(1)写成如下形式：

其中， x =[v,Θ]T为状态变量， u =[α,β]T。

将非线性时变系统(5)在参考轨迹xref处小偏差线性化，得到如下线性系统：

其中，e是x相对于参考状态量xref的偏差；下标ref表示参考量； Δu =[Δα , Δβ]T为攻角和侧滑角修正量；d是线性化带来的偏差，视作系统扰动。

A( t)和B(t)的计算方式如下：

式中：

为了便于后文的制导算法设计，本文给出了一些必要的假设。

假设1：系统(6)中的所有状态量均可以通过传感器测量。

假设2：d的大小未知但有界其中 δi为d的第i个分量的未知边界常数值。

假设3[17]：参数摄动ΔIsp、Δ、Δcx和Δcy未知，但其边界值已知。

根据以上模型处理和假设条件，构造含有不确定性的上升轨迹跟踪系统：

将微分方程系统(9)转换为微分包含系统，其表达式如下：

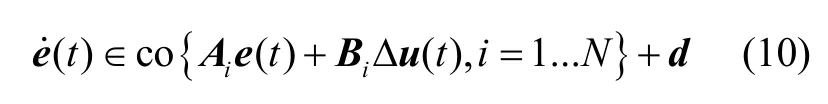
注： Ai和 Bi是由各不确定性的边界组合确定的。本文考虑不确定性个数为n = 4，则 N= 2n= 16，微分包含系统(10)可以写成N个子系统的凸组合：

其中， pi＞ 0，且

2 基于微分包含镇定的上升段轨迹跟踪控制器

基于微分包含系统(11)，本节提出一种SLV上升段参考轨迹跟踪方案。从高度动态方程=vsinΘ出发，可通过修正标称当地弹道倾角指令来消除高度偏差。本文的研究重点是设计跟踪控制算法，使其对修正后的当地弹道倾角和参考轨迹的速度指令具有良好的跟踪效果，因而这里选取PD控制器对高度指令进行跟踪。上升段轨迹跟踪控制结构框图如图1所示。

图1 上升段轨迹跟踪跟踪控制结构图Fig.1 Ascent tracking control structure diagram

2.1 基于状态反馈的多胞体线性微分包含系统有限时间有界控制律

系统(11)由两部分构成，分别是扰动d和多胞体线性系统(12)：

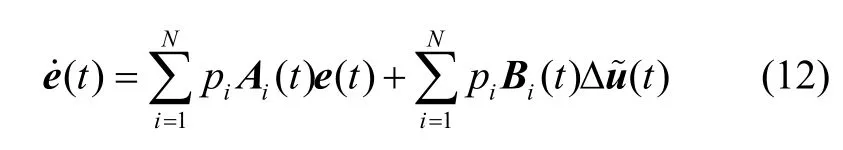
本节设计状态反馈系数K(t)，使得系统(12)有限时间收敛：

其中， Y (t)∈ R1×2和X2(t) ∈R2×2分别是有限时间收敛反馈律中引入的矩阵，可利用LMI工具箱进行求解。对Y(t)和X2(t)具体求解过程将在后面给出。

2.1.1 多胞体线性微分包含系统有限时间有界条件

定义1[18]：对于系统若：

定理1：对于系统(12)，当=0时，如果存在一个标量γ＞0和矩阵P1i＞0以及一般矩阵P2、P3，使得对所有i=1,2...N，如式(15)所示，则系统(12)关于 (c1,c2,R, T )是有限时间有界的。

和

证明：

取Lyapunov函数：

对V(t)求导，可得：

即：

其中，

则：

对式(20)，从0到t进行积分， t∈ [0,T]，有：

根据式(22)(23)可得：

因此，根据定义1，系统(12)在Δu~(t)=0是有限时间有界的。

证毕。

2.1.2 基于状态反馈的上升段有限时间有界控制律

定理2：如果存在一个标量γ＞0和矩阵 X1i＞0，以及一般矩阵X2和Y，使得对所有i=1,2...N，若有如式(25)所示的线性矩阵不等式成立，则当状态反馈的增益取 K=时，由式(12)(13)组成的闭环系统是有限时间有界的。

和

其中，

证明：

取Lyapunov函数(17)。对式(15)，取 P2= P3并记在式(15)的两边分别左乘矩阵和右乘diag{ X2, X2,I}，可得式(25)。

由式(21)可得：

由式(28)(29)，可得：

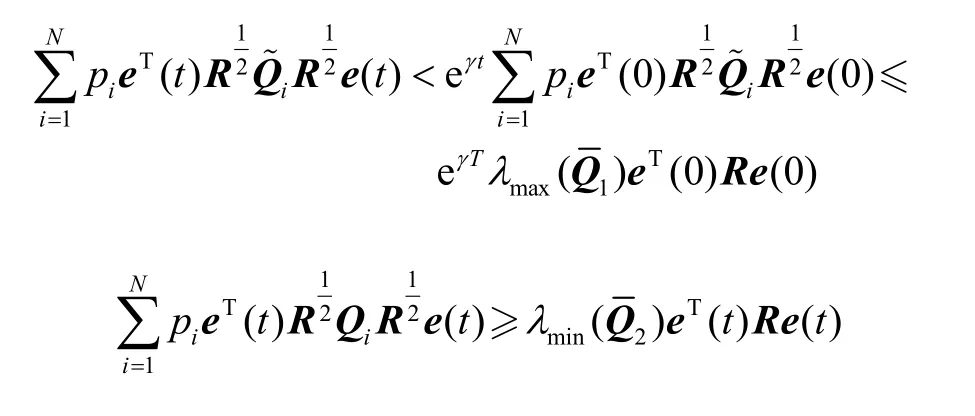
因此，有：

证毕。

通过上述分析可知，对于给定的γ值，上述控制问题转化为LMI的可行性问题。只要给定了适当的γ值，即可计算出当前时刻的状态反馈增益系数K(t)。

2.1.3 考虑控制量幅值约束的多胞体微分包含系统有限时间收敛反馈律

在实际飞行过程中，攻角和侧滑角修正量过大则可能导致SLV偏离参考轨迹过多，进而违反过载约束，因此需要对进行幅值约束。

定理3：对施加一个幅值约束，即则该约束可描述成LMI的形式：

其中，I2表示2维单位矩阵。

证明：

由Schur补引理可得：

由Schur补引理的逆定理可得：

证毕。

综上，通过式(25)(26)(31)获得的状态反馈矩阵K (t)可使系统(12)在控制量幅值约束下有限时间有界。

2.2 微分包含自适应饱和跟踪控制器

上一节针对不含扰动d的线性多胞体微分包含系统(12)设计了有限时间收敛控制器。本节针对上升段微分包含系统(11)，设计有限时间收敛控制器。在设计控制器之前，给出以下几个引理。

引理1[19]：对于任意正实数x和y，有如下不等式成立：

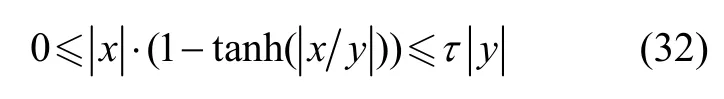
其中，tanh(·)是双曲正切函数；τ＞0，其最小值*τ满足：

其中， x*满足方程 e-2x*+1- 2 x*= 0。

引理2[20]：对于x,y∈R，有如下不等式成立：

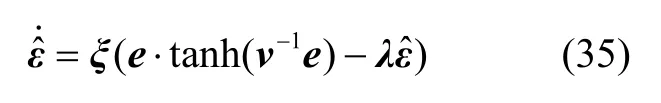
其中，K(t)由式(25)(26)(31)获得。

定理4：在控制器(37)和自适应律(35)的作用下，闭环系统(11)的状态量e(t)可以收敛至有界范围内。

其中，

证明：

取全局Lyapunov函数：

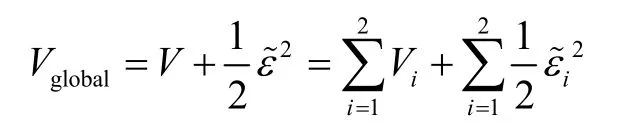
根据引理1和引理2，有：

进一步结合式(36)，有：

令：

根据式(38)(39)，有：

式(40)的左右两侧同时乘以ect并进行积分，得：

因此，跟踪误差ie收敛至有界范围内。

证毕。

3 仿真结果

SLV需要以一定的速度和当地弹道倾角将载荷运送到某一指定高度的轨道。本算例的背景是两级SLV的第二级助推阶段。发动机参数见表1。

表1 第2级发动机参数Tab.1 Engine parameters of the 2nd stage

假设第一级助推段按照离线规划产生的程序角飞行，由于发动机参数和气动系数的不确定性，高度、速度和当地弹道倾角误差在第一级结束时产生了积累。本文研究在一级累积误差和参数不确定情况下，二级轨迹的跟踪问题。终端指标为：终端高度偏差100m，终端速度偏差＜ 20m/s ，终端弹道倾角＜ 0.5°。Δα 和Δβ 的幅值约束分别为＜ 5°＜ 5°。仿真步长为1 ms，控制周期为10 ms。本节通过仿真实验，验证上升段轨迹跟踪控制器的有效性。控制器参数设置如表2所示。

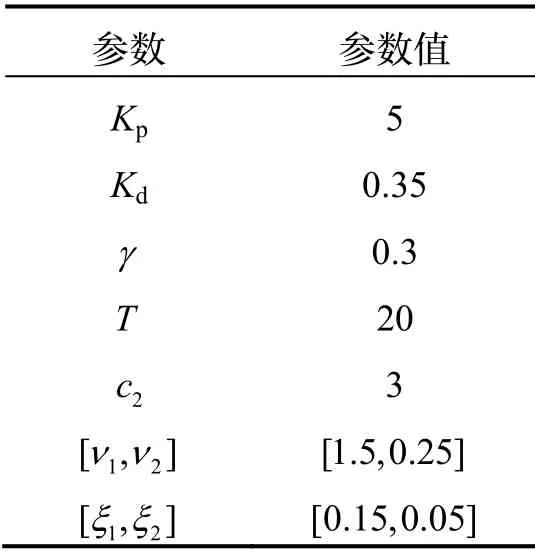
表2 控制器参数Tab.2 Controller parameters

3.1 控制器跟踪性能分析

为了验证跟踪控制器的性能，选择如下不确定性组合进行参考轨迹跟踪：

图2 -3分别为跟踪性能和控制修正量随时间的变化曲线。由图2(a)-(c)可知，在给定的不确定性情况下，控制器对高度、速度和当地弹道倾角偏差均具有良好的收敛性。因此，本文提出的微分包含跟踪控制器对复杂飞行环境和发动机不确定性参数具有良好的适应性。随着高度的增加，大气密度和气动力急剧减小，气动系数的不确定性对飞行动态的影响减弱。当发动机参数不确定性达到边界值时，相比于气动系数不确定性，发动机参数不确定性对轨迹的影响起决定性作用。因此，该算法可以抑制发动机参数带来的大不确定性。然而，由于发动机参数的不确定性始终存在，终端速度偏差不能完全控制收敛至0。控制器将速度偏差控制在[-2,2] m/s范围内。由于参考轨迹的终端速度和终端当地弹道倾角分别为6420 m/s和0°，控制器对Θref进行跟踪且 Θref(tf) = 0，则可以粗略估计为＜ arctan(2 vref(tf)) = 0.0179°，终端当地弹道倾角偏差极小。由式(1)可知，当地弹道倾角偏差由直接Δα 控制。因此当当地弹道倾角偏差趋近于零时，攻角也趋近于零，如图3(a)所示。Δβ≠0是为了控制始终存在的速度偏差，如图3(b)所示。此外可以得出，在不同条件下，速度偏差的收敛程度主要取决于发动机参数摄动。

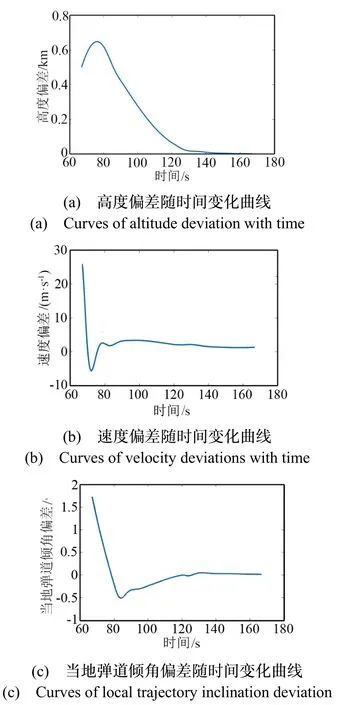
图2 微分包含跟踪控制器性能Fig.2 Differential inclusion tracking controller performance

图3 控制量随时间变化曲线Fig.3 Curves of control variable over time

3.2 鲁棒性能分析

为了进一步验证控制器的鲁棒性，进行了蒙特卡洛仿真试验。参数不确定性的分布情况如下：

ΔIsp～U(-2.5s,+2.5s), Δm˙～U(-0 .45kg/s,+0.45kg/s)

Δcx～U(-25%,+25%), Δcy～U(-25%,+25%)

其中，U表示均匀分布。

图4 给出了在500次蒙特卡洛仿真试验下，高度、速度和当地弹道倾角随时间变化的曲线。由图4可知，在给定的不确定性范围内，所有轨迹的高度、速度和当地弹道倾角偏差均收敛。由于 Ai(t )和Bi(t)由不确定性边界值计算得到，因此当不确定性在给定的边界值范围内时，控制器可以对边界内的所有不确定性组合进行镇定。如果将各不确定性组合看作上升段微分包含系统的子微分方程系统，结果进一步表明微分包含系统的镇定过程是它所包含的任意子微分方程系统的镇定过程。终端状态误差的范围如表3所示。

表3 蒙特卡洛仿真下的终端误差Tab.3 Terminal errors in Monte Carlo simulation

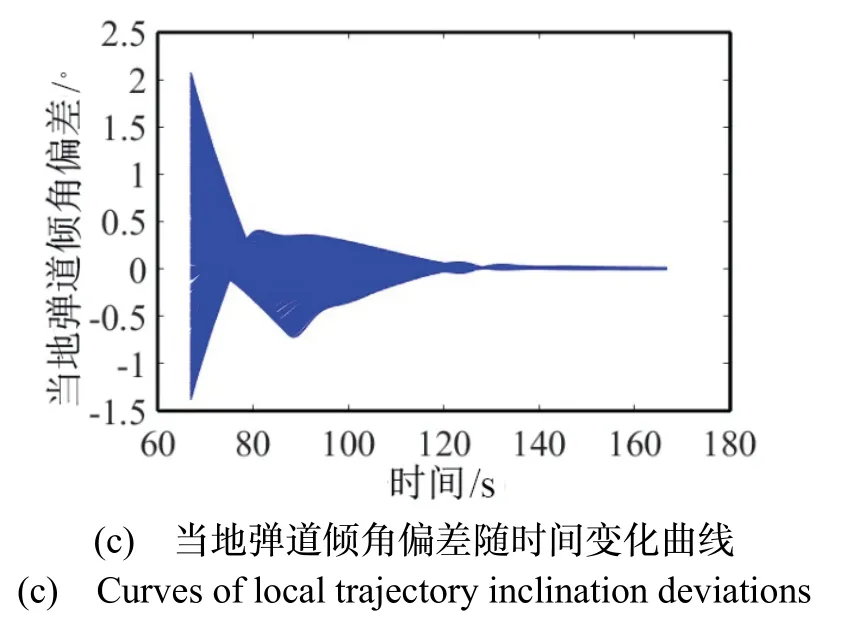
图4 蒙特卡罗仿真下的跟踪性能结果Fig.4 Monte Carlo result of tracking performance

3.3 方法比较

本节将本文提出的微分包跟踪控制器（控制器1）和基于扩张状态观测器的跟踪控制器(控制器2)[20]方法进行对比。控制器2将所有不确定性引起的扰动作为一个整体处理，通过设计ESO对其进行估计并进行补偿。文献[20]只考虑气动力偏差，为了达到比较效果，这两种算法均考虑了发动机比冲和秒流量的不确定性。分别在表4中给定的情况下，对两种控制器进行对比。

表4 发动机和气动参数摄动Tab.4 Engine and aerodynamic parameter perturbations

两种控制器的跟踪效果如图5所示，蓝色、红色、黄色和绿色曲线分别代表场景1-4。由图5可知，在场景1和2下，控制器2的跟踪性能优于控制器1。控制器2算法的高度和速度收敛速度均快于控制器1，且控制器2具有较高的终端精度。这是因为当不确定性较小时，ESO能够准确估计不确定性产生的扰动并进行精确补偿。当不确定性进一步增大时（例如场景3和4），控制器2无法精确跟踪参考轨迹。其原因是，发动机参数的不确定性对上升段动态过程的影响较大，当发动机参数摄动范围较大时，固定参数的ESO在较宽的不确定范围内无法保证良好的观测性能。因此，当不确定性的边界范围较大时，场景3和4中控制器2算法的鲁棒性变差。与传统的估计-补偿方法相比，本文提出的控制器虽然具有保守性，但当某一确定性组合处于给定的边界内，可使该情况下的状态偏差收敛。

图5 两种控制器的跟踪性能Fig.5 Tracking performance of two controllers

4 结 论

本文提出了一种基于微分包含镇定的轨迹跟踪控制器，仿真结果表明，该控制器适用于SLV上升段制导问题，对参考轨迹的高度、速度和当地弹道倾角具有良好的跟踪效果。结合发动机参数和气动系数的不确定性，给出了上升段轨迹跟踪问题的微分包含描述方法，并将上升段轨迹跟踪问题转化为微分包含镇定问题。针对微分包含系统，设计了微分包含自适应饱和跟踪控制器并证明了其闭环稳定性。在给定的不确定边界内，该控制器能够实现在任意不确定性组合下，速度和当地弹道倾角偏差收敛至有界范围内，实现了实际轨迹对参考轨迹的实时跟踪。在仿真算例下，终端速度、当地弹道倾角和高度误差分别小于2 m/s、0.01 °和10 m，均满足指标要求。与基于ESO的观测-补偿方法相比，本方法拓宽了不确定性的适用范围。