基于仿射因子补偿的改进地形匹配ICCP算法

程向红，王依能，丁 鹏

（1. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096；2. 东南大学 仪器科学与工程学院，南京 210096）

水下航行器在军用和民用领域具有重要战略意义，随着地球物理场辅助惯性导航技术的不断发展，应用地磁、重力、地形等信息来辅助惯性导航系统为水下航行器导航技术研究提供了一种新思路[1]。由于地形高程信息测量较为方便，且陆地上的地形匹配技术已应用于实际，可以为水下地形匹配导航技术提供借鉴[2]，因而应用地形高度信息来辅助水下航行器的导航技术具有高度可行性。

目前，地球物理场辅助导航方法主要有地形轮廓匹配算法（Terrain Contour Matching, TERCOM）、桑迪亚惯性地形辅助导航算法（Sandia Inertia Terrain-aided Navigation, SITAN）和迭代最近等值线算法（Iterated Closest Contour Point, ICCP）。TERCOM实时性差[3]，且对于航向误差较为敏感；SITAN系统则对初始位置精度要求高[4]，且要求对地形做线性化估计，当地形斜率的正负号变化时则会导致滤波发散。

ICCP算法由ICP（Iterated Corresponding Point）算法发展而来，最早由Besl和McKay在图像对准领域使用，随后被Behzad K. P.[5]首次应用于重力匹配辅助导航，Bishop通过大量仿真试验，系统地分析了该算法的可行性及误差影响[6]，刘承香进一步详细分析了ICCP算法在地形匹配辅助导航领域的适用性[7]。考虑到匹配过程中因为速度误差会导致惯导指示航迹与真实航迹的形状存在不同[8]，罗诗图等采用最小失配点准则估计仿射变换参数，但精度不高[9]，此外模拟退火[10]、最小二乘等最优估计算法[11]精度优于最小失配点准则，但需要较长的计算时间。因此，为了尽可能得到精度高的仿射因子，同时很好地保证算法的实时性，本文首先对ICCP算法的原理与缺陷进行分析，接着对仿射模型进行数学分析，推导得出仿射因子的解析解，用仿射因子补偿匹配过程中的仿射误差，提出改进算法模型，最后进行试验验证并给出结论，验证改进算法提升匹配精度的效果。

1 ICCP算法

1.1 ICCP算法原理

ICCP的基本实现原理可以理解为，从数据形态中抽取出若干点构成点集1，从模型形态中抽取同等数目的若干点构成点集2，并设置初始的迭代参数，不断循环进行计算点集1与点集2中各对应点的最近点、计算对准变换、应用对准、判定精度的步骤，当迭代结果变化低于预先设定的门限值时停止迭代、完成匹配[12]。

算法实现示意图如图1所示，当水下航行器进入适配区后，通过航行器携带的测深传感器测量并存储航行轨迹点对应的水深值，根据惯性导航系统提供的位置提取所在区域的水深数据库，再根据实测水深值hi，在水深数据库中提取惯导指示航迹点pi附近的等值线ci，并在等值线ci上搜索到pi的最邻近参考点yi。其中，i = 1, 2… N表示第i个惯导指示航迹点序号，hi表示第i个航迹点所对应的实测水深值，pi表示第i个惯导指示航迹点所对应的二维位置坐标，ci表示第i个指示航迹点附近对应实测水深值hi的等值线，yi表示第i个指示航迹点到等值线ci上的最邻近参考点的二维位置坐标。

图1 ICCP算法实现示意图Fig.1 ICCP algorithm implementation

根据从参考数据库中搜索的最邻近参考点与惯导指示航迹点确定旋转矩阵R和平移向量t，使得最邻近参考点集合Y与惯导指示航迹点集合P之间的欧几里得距离平方和最小，公式如下：

式中，Y={yi, i = 1, 2… N}表示最邻近参考点集合，P ={pi, i = 1, 2… N}表示惯导指示航迹点集合，d表示集合Y和集合P的欧几里得距离平方和，表示向量X的2范数。

利用矩阵的特征值特征向量分解方法得到旋转矩阵R，首先对惯导指示航迹点pi和最邻近参考点yi作一个变换，即令：

然后根据相对二维位置坐标Δpi和Δyi构造一个2×2矩阵M，即：

式中，M是由坐标变换后的惯导指示航迹点Δpi和最邻近参考点Δyi构成的2阶方阵，右上角标T表示矩阵的转置。

接着构造一个4×4矩阵H：

M11、M12、M21、M22是矩阵M的元素，矩阵H的四个特征值易证是实数，如下所示：

记最大的特征值为λm，由特征向量与旋转角、旋转矩阵的单位四元数表示法之间的关系，可得旋转角θ与旋转矩阵R为：

平移向量t为：

基于上述原理表述可以看出，ICCP算法遵循“初始对准—寻找对应关系（最近点）—求解使得目标函数最小的变换—应用变换”的循环过程[13]，在等值线上寻找最小度量意义下的全局最优值，该全局最优值就是最终的匹配对准结果。

1.2 ICCP算法的局限性

水下航行器进入匹配区域后，由于惯导误差随时间不断积累，导航定位结果本身会携带位置误差Δp0、速度误差δv与姿态误差ψ，速度方程可表示为：

鉴于短时间内姿态误差的累积量较小，ICCP算法每一次迭代过程中惯导航向误差的变化可以忽略，因而航向误差可看作常值；ICCP算法仅对水下航行器的水平方向位置进行对准匹配，姿态误差ψ对匹配结果几乎没有影响。在以上两点的假设基础上，速度误差的变化εv可以看作随时间t线性变化，进一步可以用其数学期望εm来表示，因此速度误差与速度方程可以表示为：

假设配准开始是为0时刻且采样间隔为ΔT，那么水下航行器的位置更新方程离散形式可以表示为：

Δp0为位置误差，将式(11)(13)代入式(12)可得：

式中，Δp0+Δv(k+1)ΔT两项为最终的位置匹配误差，Δp0是匹配前的系统位置误差，Δv(k+1)ΔT是由速度误差造成的累积误差。在实际的轨迹匹配中，Δp0表现为平移误差，Δv(k+1)ΔT表现为旋转误差和仿射误差，轨迹匹配过程中的旋转误差在上述分析中被认为是常值。

根据1.1中旋转矩阵R和平移向量t的定义，平移向量t的离散形式即为位置误差Δp0，同时令仿射因子为s，那么(k+1)时刻和k时刻的惯导系统指示位置可改写为：

对比式(14)和式(15)，可以得出惯导系统速度误差造成的累计误差Δv(k+1)ΔT与仿射因子s之间的关系为：

但由于ICCP算法本身只考虑了匹配变换过程中的平移误差与旋转误差，并未修正由速度误差引起的仿射误差，因此传统的ICCP匹配算法只能对惯导指示航迹做刚性轨迹匹配，精度有限[14]。针对这一局限性，可以在现有ICCP算法的基础上引入仿射模型与仿射因子，对于由惯导轨迹到真实轨迹的变换进行优化，修正仿射误差，提高匹配精度。

2 仿射因子解析解

鉴于传统ICCP算法不能修正速度误差带来的仿射误差，因此需要借助仿射变换模型对仿射误差进行补偿。而引入仿射变换模型后，改进ICCP算法的核心即为求解旋转矩阵R、仿射因子s和平移向量t，使得最邻近参考点集合Y与惯导指示航迹点集合P之间的欧几里得距离平方和最小，公式如下：

旋转矩阵R的求解方式与1.1中保持一致，最邻近参考点集合Y与惯导指示航迹点集合P之间的欧几里得距离平方和d(Y,sRP+t)，也即集合Y与集合P之间误差ei的平方和，可以改写为如下形式：

其中平移向量的误差Δt为：

由此可以得到：

根据刚性变换不改变长度模值的特性：

可将式(20)改写为：

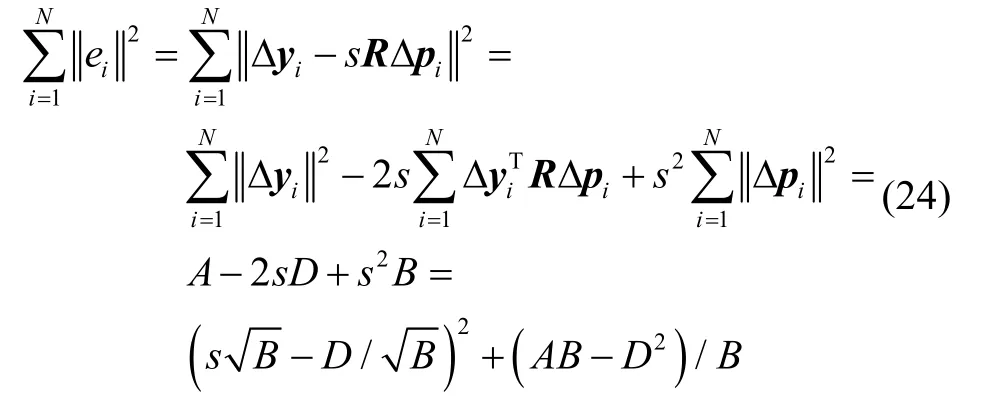
3 改进ICCP算法

在旋转矩阵R、仿射因子s和平移向量t的基础上，基于仿射因子补偿解的改进ICCP算法流程图如图2所示。改进ICCP算法以组合导航系统为平台，借助水深参考数据库对惯导航迹进行匹配对准：

图2 改进ICCP算法流程图Fig.2 Flow chart of the improved ICCP algorithm

第一步：水下航行器进入适配区后，通过水深传感器测量并存储航行轨迹点的水深值，根据惯导系统提供的位置信息提取所在区域的水深参考数据库；

第二步：根据实测水深值提取惯导指示航迹点附近的等值线，并搜索指示航迹点到附近等值线上的对应最邻近参考点；

第三步：根据从参考数据库中搜索的最邻近参考点与惯导指示航迹点确定旋转矩阵R、仿射因子s与平移向量t；

第四步：利用第三步得到的旋转矩阵R、仿射因子s与平移向量t更新指示航迹点的位置，判断迭代次数是否超限或满足局部最优条件，迭代允许的最大次数由匹配过程的实时性要求以及实际操作经验确定，一般可取10~20次，局部最优条件是当前匹配航迹相较于惯导指示航迹点组成的航迹的欧几里得距离平方和的变化率小于特定值εsop，εsop的具体数值根据地形图网格精度、惯导器件误差、初始位置误差等实际情况确定，试验验证中取εsop为5%，如果没有达到迭代次数或没有满足收敛条件，则返回第二步进行循环操作，否则进入下一步；

第五步：对最后得到的航迹进行精度评估，判断结果是否可靠，如果最终的匹配航迹相较于上一次迭代得到的匹配航迹（若为第一次迭代，则与惯导指示航迹点组成的航迹比对）的欧几里得距离平方和小于特定值εop则认为结果可靠，εop的具体数值根据地形图网格精度、惯导器件误差、初始位置误差等实际情况确定，试验验证中取εop为五分之一个网格精度，最后得到的匹配航迹可用以校正惯导指示航迹，否则认为匹配失败，需要放弃当前航迹，使用其他航迹重新进行匹配。

4 试验验证

4.1 仿真试验

为了验证本文所提方法的有效性，选取某海域的水深数据库进行仿真实验，设置INS待匹配轨迹的采样点数为3200个，两点之间的采样间隔为0.01 s，即仿真轨迹持续32 s。仿真实验参数如表1所示。

表1 仿真试验参数Tab.1 Simulation experiment parameters

规划不同的水下航行器运动轨迹，进行5次相同仿真参数、不同运动轨迹的仿真试验，利用传统ICCP算法与基于仿射因子补偿的改进ICCP算法进行轨迹匹配，验证改进算法的匹配效果，不同轨迹下的匹配精度数据如表2所示。5条水下航行器轨迹匹配仿真图具有类似的情况，选其中轨迹1的轨迹匹配结果绘图展示，如图3-4所示。

表2 不同轨迹的匹配结果Tab.2 Matching results of different trajectories

图3 水下航行器轨迹匹配仿真图Fig.3 Simulation of underwater vehicle trajectory matching

图4 匹配轨迹点位置误差比较图Fig.4 Comparison of matching points' positioning errors

根据轨迹1的轨迹匹配仿真图，可以看出ICCP匹配轨迹、基于仿射因子补偿的改进ICCP匹配轨迹与理论航迹都具有类似的形状，都能一定程度上修正INS待匹配航迹，但改进ICCP匹配航迹更加接近水下航行器的仿真理论真实航迹。根据匹配轨迹点位置误差比较图，则更明显地看出改进ICCP算法的匹配结果远好于传统ICCP算法，传统算法的轨迹点位置误差在80 m到120 m波动，而改进算法位置误差小于40 m。

结合表2中不同轨迹匹配结果的均方根位置误差具体数据，可以验证本文提出的基于仿射因子补偿的改进ICCP方法很好地修正了传统ICCP算法中的仿射误差，相比于传统算法的结果，改进ICCP算法的匹配精度有80%以上的提升；并且以数学推导求解仿射因子的方式并未带来过多的运算量，传统算法与改进算法的时间复杂度差别不大，利用蒙特卡罗法进行多次模拟可以得到改进算法平均耗时约为1.7391 s，相对于传统算法1.7235 s的平均耗时，仅增加不到1%。

4.2 半物理仿真试验

在纯仿真实验验证本算法的可靠性之后，基于浙江省千岛湖新安江水库部分区域的实际水下地貌与船载实验数据，进一步验证本算法在实际系统中的效果。

表3 中记录了船载实验中惯性导航系统的设备参数及地形图网格间距，这里选用一段曲折程度较大的轨迹进行半物理仿真试验，意在从图中直观体现出仿射因子对于匹配前后轨迹形态的影响。轨迹采样点设置类似4.1中的仿真试验，总采样点4800个，两点间采样间隔为0.01 s，即所选航行轨迹持续48 s。

表3 船载试验参数Tab.3 Shipboard experiment parameters

图5 为基于船载实验数据的半物理仿真图，相较于INS待匹配航迹与ICCP匹配航迹，可以明显看出本文提出的改进ICCP算法得到的匹配航迹匹配误差小、更贴合理论航迹。图6为轨迹点位置误差比较图，同样可以看出：传统ICCP算法的位置误差波动幅度大，误差值基本保持在50 m以上；改进ICCP算法的位置误差则较为稳定，始终保持在50 m以内。

图5 轨迹匹配半物理试验图Fig.5 Semi-physical experiment of trajectory matching

图6 匹配轨迹点位置误差比较图Fig.6 Comparison of matching points' positioning errors

经过计算，传统ICCP算法匹配后均方根位置误差为127.8 m，耗时约为2.5366 s；改进ICCP算法匹配后均方根位置误差为27.4 m，耗时约为2.5518 s。改进算法的匹配精度比传统算法提升了78.6%，而算法耗时仅增加0.6%。由此可以表明：改进ICCP算法在实际系统中仍然能够以很小的时间代价，带来较大的匹配精度提升。

5 结 论

本文介绍了ICCP算法的实现原理，对配准误差进行理论分析，得出其刚性变换的局限性，并研究仿射变换模型，引入仿射因子的解析解，修正刚性变换未能解决的仿射误差。通过仿真试验与半物理试验验证了本算法的有效性，半实物仿真试验结果表明：基于仿射因子补偿的改进ICCP算法可以在算法耗时增加不到1%的前提下，修正航迹匹配过程中的仿射误差，匹配精度较传统的ICCP算法平均提高78%以上，在10 m网格的水深图中，传统算法匹配精度在10个网格精度左右，改进算法的匹配精度可达到1~2个网格精度。