基于地球重力场模型的重力匹配数据随机线性化方法

黄 炎，李姗姗，谭勖立，王傲明，范 雕，付林威

（中国人民解放军战略支援部队信息工程大学 地理空间信息学院，郑州 450001）

惯性/重力/重力梯度组合导航系统由于其无源、自主、隐蔽性好和不受时域限制等优势，成为了水下潜航器定位导航研究的重点[1]。重力匹配算法均是以地形匹配算法为基础发展而来，主要匹配算法有：基于相关分析技术的地形轮廓匹配（Terrain Contour Matching, TRECOM）算法、迭代最近等值线点（Iterated Closest Contour Point, ICCP）算法和基于递推滤波技术的桑迪亚惯性地形辅助导航（Sandia Inertial Terrain Aided Navigation, SITAN）算法[2,3]。经过国内外学者的研究与改进，重力匹配导航算法得到了快速发展，不仅对上述三种匹配算法进行了改进，提高了匹配精度，还相继提出了矢量匹配算法、具有约束条件的匹配算法以及基于人工智能的蜂群匹配算法等[4]。

由于水下潜航器定位导航对实时性的要求较高，目前国内主要利用滤波技术进行重力匹配导航，其中以SITAN算法为基础的扩展Kalman滤波（Extended Kalman Filter, EKF）算法以其实时性好、敏感度高的优势被广泛研究和应用[5]。EKF算法核心技术由两部分构成，一是重力随机线性化技术、二是Kalman滤波技术。因此其显著缺点也与SITAN算法相似，即EKF算法仅是将非线性的观测方程在惯导指示位置利用随机线性化技术进行线性化处理，而不考虑重力场固有属性以及随机变量的验前误差，因此会产生较大的线性化误差，从而导致滤波性能损失，甚至快速发散无法得到较好的结果。

地球重力场模型是用一个截断到有限阶次的引力位球谐函数级数来逼近地球重力场[3]，其中，EIGEN-6C4地球重力场模型是一个不仅包含了LAGEOS、GRACE、GOCE等卫星测高、重力、重力梯度卫星数据，还包含了实测海洋重力数据，并在DTU全球重力异常数据以及EGM2008地球重力场模型的基础上，构建到了2190阶的超高阶地球重力场模型。该地球重力场模型包含大量实测数据，能够在一定程度上反映真实地球物理场信息，因此，本文选用EIGEN-6C4地球重力场模型用以反映重力场包含的物理信息，并利用其对重力和重力梯度进行线性化处理。

1 重力EKF匹配导航算法

由于水下潜器航行的隐蔽性需求，重力和重力梯度测量不需要对外界发出信号，具有较好的无源性，且地球重力场相对稳定，不会产生较大的波动，因此重力和重力梯度辅助惯性导航成为水下潜航器无源自主导航的重要研究内容，其流程图如图1所示。

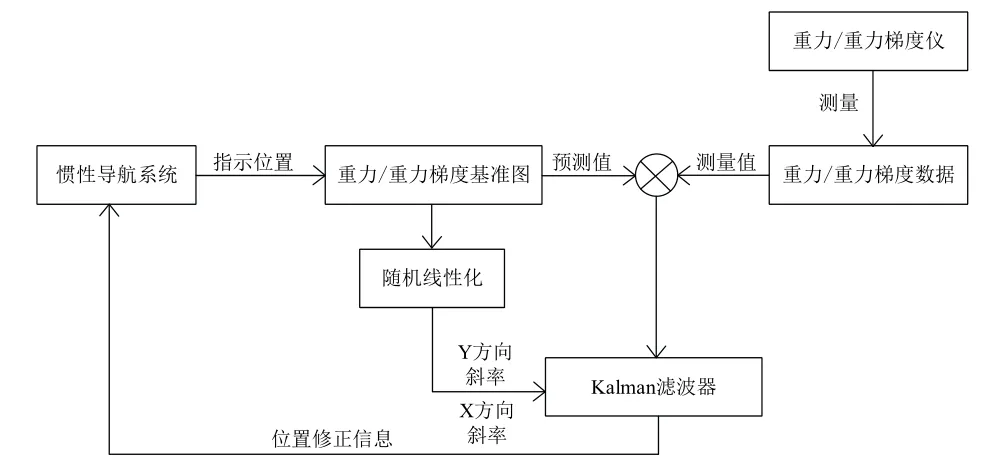
图1 重力匹配EKF算法Fig.1 Gravity matching EKF algorithm

1.1 EKF状态方程构建

重力/重力梯度信息对速度误差的反应不够敏感，因此，本文仅选用 X=(δφ,δλ)T作为滤波状态变量，式中δφ、δλ分别表示水下潜航器的纬度误差和经度误差。

由惯性导航误差方程和滤波状态变量可知，惯性导航系统定位导航位置平面误差微分方程表达式如式(1)所示。

式中，ve表示东向速度，RN表示指示位置点卯酉圈曲率半径，φ表示地心纬度，Wφ与Wλ表示由系统噪声产生的纬向和经向误差。

将式(1)化简为：

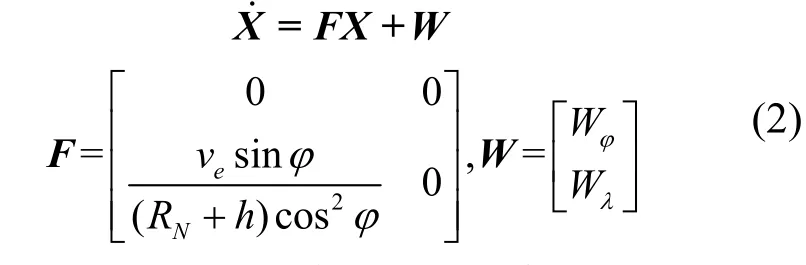
若滤波周期为T，则将式(2)进行离散化处理后可得：

式中，Φk/k-1表示状态转移矩阵，可由系统状态矩阵F通过Laplace变换得到 Φk/k-1= I +F＊T。

1.2 EKF量测方程构建

由于地球重力场是一个与位置有关的连续物理场，因此，假设水下潜航器真实位置的重力异常和重力梯度（本文均以重力梯度垂直分量Tzz为例）在惯导指示位置点(φi,λi)的邻域内存在一阶导数，利用泰勒级数将其展开可得：

式中，φt、λt分别表示潜航器真实位置点处的纬度和经度；vgi与vTi表示泰勒级数展开过程中的截断误差，ΔgM(φi,λi)与 TzzM(φi,λi)表示利用惯导指示位置坐标在重力异常和重力梯度基准图上提取出的重力异常值和重力梯度垂直分量值，Δ g (φt,λt)与 Tzz(φt,λt)则表示水下潜航器真实位置处的重力异常值和重力梯度垂直分量值。

又因为水下潜航器自身搭载有重力仪以及重力梯度仪，因此，Δg(φ,λ)与 Tzz(φ,λ)又可以由如式(5)所示。

式中，vgs与vTs表示由于重力仪和重力梯度仪测量产生的观测误差， Δgs(φt,λt)与 Tzzs(φt,λt)表示由重力仪和重力梯度仪测量并计算得到的重力异常和重力梯度垂直分量观测值。

由式(4)(5)即可得到重力异常和重力梯度垂直张量组合匹配导航的滤波观测方程分别为：

同理亦可得到重力异常与任意重力梯度张量间的组合匹配滤波观测方程。

2 基于地球重力场模型的随机线性化技术

2.1 随机线性化原理

随机线性化技术原理如图2所示。

图2 随机线性化原理示意图Fig.2 Schematic diagram of stochastic linearization principle

重力匹配导航的本质是通过重力基准图与重力仪实时测量数据的匹配实现对惯性导航系统的校正，由于地球重力场是关于位置的非线性函数。因此在利用Kalman滤波进行匹配导航建立量测方程时，首先需要获得量测值（重力场值）与状态参数 X=(δφ,δλ)T之间的线性关系，即对重力场与位置之间的非线性关系进行线性化，而线性化过程的准确与否又直接关系到量测方程是否构建准确。常用的随机线性化技术有一阶泰勒展开法、九点拟合法、全平面拟合法、平均切线法等[6]，同时也有学者针对地球重力场非线性特性，提出了双二次曲面拟合等方法[5]。双二次曲面法是在泰勒展开法的基础上，考虑了重力场的非线性特性，利用一个二次曲面对区域进行拟合，从而削弱线性化截断误差的影响。

由于重力场中大量相关信息的缺失，上述随机线性化方法对匹配点纬向和经向“斜率”的估计会存在较大的误差，从而使得滤波不准确乃至发散。而利用EIGEN-6C4地球重力场模型进行计算，不仅包含了LAGEOS、GRACE、GOCE等卫星测高、重力、重力梯度卫星数据，还包含了实测海洋重力数据，能够最大程度地利用实测数据反映地球重力场特征，适用于水下重力/重力梯度匹配导航。

2.2 基于重力场模型的线性化方法

地球重力场模型是利用现有实测重力场相关数据利用反演的方法，用一个截断到有限阶次的球谐级数式来逼近地球重力场[3]。以一个半径等于地球平均半径R的球来近似表示地球，可以得到如下扰动引力位球谐级数表达式：

式中，ρ、φ、λ分别表示空间任意一点的地心向径、地心纬度和经度，表示完全正常化的缔合勒让德函数，表示地球重力场模型。因此可以得到任意一点的重力异常Δg与扰动重力梯度垂直分量Tzz与扰动位T之间的范函关系如下：

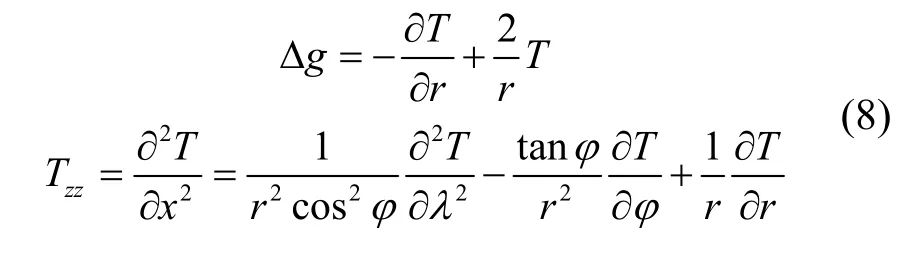
此次计算对象是海洋重力数据，可近似认为（ R / r）≈ 1。将式(7)带入式(8)可得：

式中，

利用地球重力场模型对重力异常以及扰动重力梯度进行线性化，就是求得重力异常与扰动重力梯度在纬向和经向的导数和，式(9)两式左右同时对φ和λ求偏导可得：

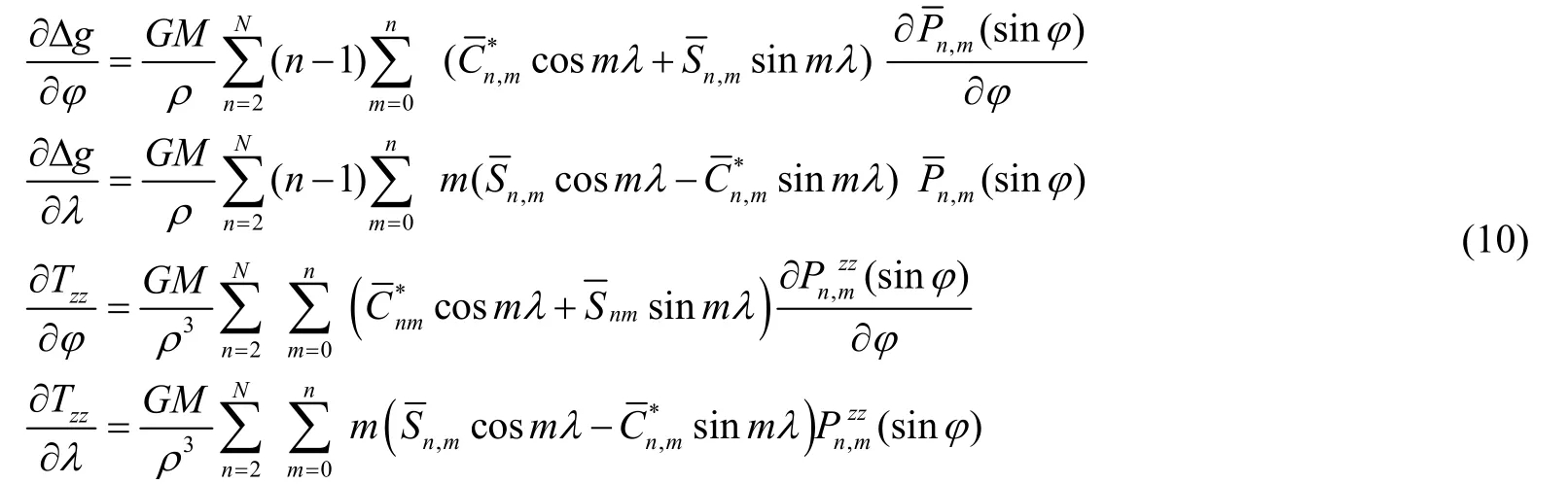
式中，

利用式(10)即可完成基于重力场模型的随机线性化计算。

2.3 线性化方法并行加速方案

利用地球重力场模型进行随机线性化的计算速度对于重力/重力梯度匹配导航的实时性要求还有一定差距[7-9]。因此，为了有效提高地球重力场模型线性化的计算效率，本文提出基于矩阵运算的GPU并行计算方案，首先将式(10)标量运算推导至矩阵运算形式，并利用GPU对矩阵运算过程进行并行化处理提高计算效率。

2.3.1 随机线性化矩阵计算公式

而为了使得式(10)左右两端矩阵行列相等，则需要对等式左端和进行拆分，拆分方法如下式：

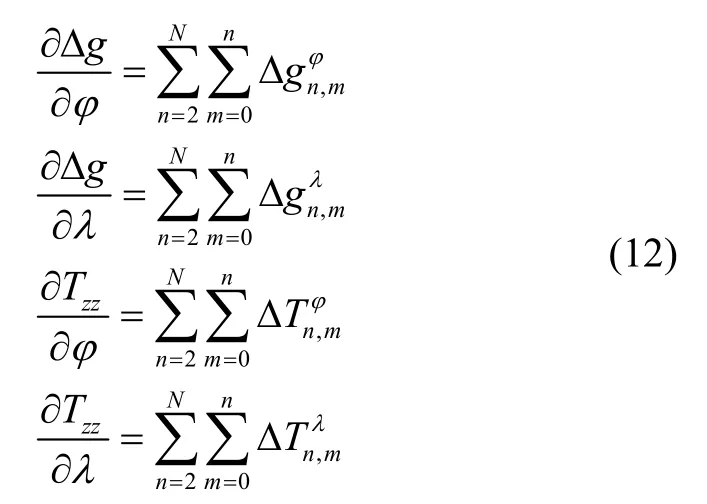
将式(11)(13)带入式(10)得：

式中，“°”表示矩阵对应元素相乘。

式(14)即为利用地球重力场模型进行随机线性化计算的矩阵计算公式。

2.3.2 基于GPU的并行加速方案

本文选用CUDA对上述矩阵运算过程进行并行化。CUDA是英伟达公司推出的CPU+GPU异构并行编程平台，其可以充分发挥GPU的计算能力，在各个领域得到了广泛的应用[10-12]。在使用CUDA按照式(17)矩阵计算公式进行计算时需要将矩阵空余部分用“0”补齐，因此在计算中有一半的线程在做“无用”计算，极大的浪费计算能力。因此本文提出“矩阵拆补法”并行计算方案，将n+1行m+1列的下三角矩阵按照一定的规则，差分并重新补齐为一个（ n+ 2）/2行m+1列的矩阵，如图3所示。若n为偶数，则将下三角矩阵的前n/2行进行拆分，其中第i行补至第n+1-i行，组成一个新的n/2+1行m+1列的矩阵；若n为奇数，则将下三角矩阵的前（n-1）/2行进行拆分，其中第i行补至第n+1-i行，第（n+1）/2行用0元素补齐，组成一个新的（ n+ 1）/2 +1行m+1列的矩阵。以截断阶数N=8为例，将下三角矩阵前4行进行拆分，将第1行补至第8行，将第2行补至第7行，将第3行补至第6行，将第4行补至第5行，组成一个5行9列的新矩阵。

图3 矩阵差补法示意图Fig.3 Schematic diagram of matrix splitting and complement method

通过并行计算方案，即可完成地球重力场模型线性化并行计算。

2.3.3 并行加速效果

为验证上述GPU并行计算方案有效性，本节利用笔记本电脑，处理器为Intel(R) Core(TM) i7-8750H CPU @ 2.20GHz；GPU为NVIDIA RTX 2070；内存16.00GB。软件环境为64位Windows 10操作系统，VS2013 + CUDA9.2平台。利用串行方案与本节所提GPU并行方案计算不同阶数和计算耗时与加速比如表1所示。

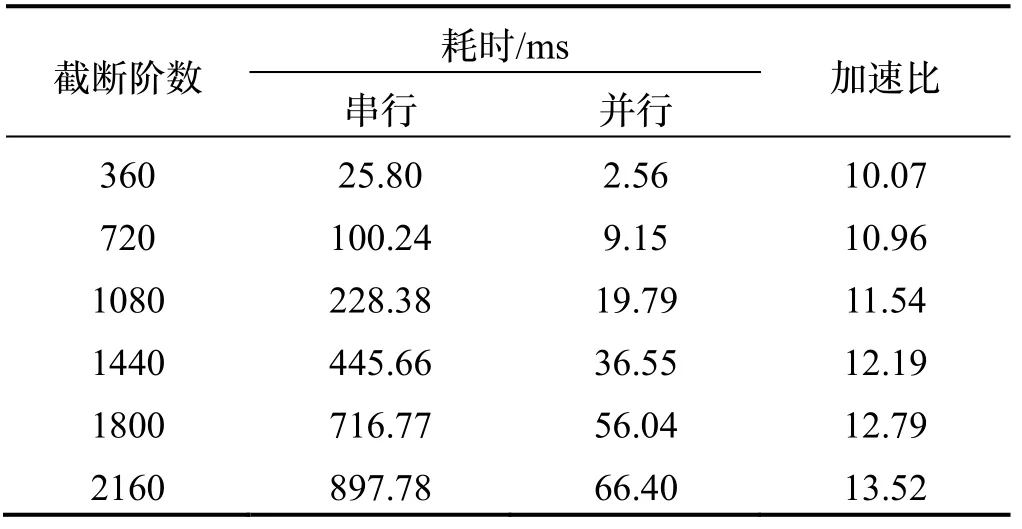
表1 地球重力场模型线性化计算耗表Tab.1 Linearization calculation of earth gravity field model

由表1可知，利用本文所提GPU并行计算方案进行随机线性化计算加速比均在10倍以上，最高可达13.52倍，计算360阶线性化参数仅需2.56 ms，计算2160阶线性化参数仅需66.40 ms。充分证明了本文所提GPU并行计算方案的有效性。

3 重力场模型线性化实验验证与分析

利用惯性/重力/重力梯度组合导航仿真程序进行水下潜航器航迹轨迹与测量数据仿真，惯性导航采样率为100 Hz。仿真数据包含惯性元器件输出（角增量与速度增量）、重力异常观测数据、重力梯度观测数据以及水下潜航器真实航迹[13]。重力异常基准图选用丹麦科技大学（Technical University of Denmark, DTU）利用卫星测高数据、实测重力异常数据等反演计算发布的DTU18全球重力异常模型，数据分辨率1'，中误差2~3 mGal[14]。重力梯度基准图则在EIGEN-6C4地球重力场模型与DTU18全球重力异常模型基础上，基于Stokes理论利用移去-恢复技术计算得到，数据分辨率计算至1'。惯性元器件误差设置如表2所示。

表2 惯性元器件误差设置Tab.2 Error setting of inertial components

当前，海洋重力仪动态测量精度已达到1 mGal（如德国的KSS系列和美国的L&R系列重力仪），因此重力仪测量误差一般取标准差为1 mGal的白噪声，此外还需要增加一个误差项用以表示由于厄特弗斯改正等因素造成的影响，根据经验取为3 mGal。重力梯度仪的动态测量精度可达到7E（如美国的HD-AGG和英国的EGG系列重力梯度仪），因此重力梯度仪测量误差取标准差为7E的白噪声。同时结合本文所用的重力与重力梯度基准图分辨率以及水下潜航器的航行速度，EKF量测方程更新时间间隔选取180 s（即每隔180 s进行一次组合匹配导航校正）。惯导解算采用双子样算法，每次惯导更新均进行一次状态方程更新，因此EKF状态方程更新时间间隔为0.02 s。

选择重力异常Δg与重力梯度垂直张量Tzz作为滤波观测量，仿真试验区选在某海域，区域大小为2.5°×4°，试验区重力异常与重力梯度垂直张量基准图如图4所示。

图4 试验区基准图Fig.4 Reference map of test area

分别生成两条航迹，航迹1的航行时长4小时，初始速度与姿态分别为（0 m/s，0 m/s，0 m/s）和（0 °，0 °，0 °），起始坐标为（0.5 °，0.5 °，-100 m），潜航器沿着正北方向先以0.0086 m/s2的加速度，匀加速600 s，速度达到10节/h，然后匀速直线航行3h 3000s；航迹2的航行时长24小时，初始速度与姿态分别为（0 m/s，0 m/s，0 m/s）和（0 °，0 °，-10 °），起始坐标为（0.5 °，0.4 °，-100 m），潜航器沿着北偏东45 °方向先以0.0086 m/s2的加速度，匀加速600 s，速度达到10节/h，然后匀速直线航行11 h 3000 s后，右转45 °，转弯时长300 s，再匀速航行11 h 3300 s。

3.1 EKF-mx不同截断阶数匹配效果分析

在试验区域内以航迹1为实验对象，选取重力异常与重力梯度垂直分量作为观测量，分别使用360阶、720阶、1080阶、1440阶、1800阶和2160阶重力场模型进行随机线性化，计算并统计匹配航迹位置相较于参考位置的纬向误差Δy、经向误差Δx以及导航定位误差航迹1航行4 h，初始误差设置为0.4 n mile，重力匹配校正79次，对重力匹配校正位置的误差进行统计，结果如表3所示，并绘制误差曲线如图5所示。

图5 不同截断阶数匹配误差Fig.5 Matching error of different truncation orders

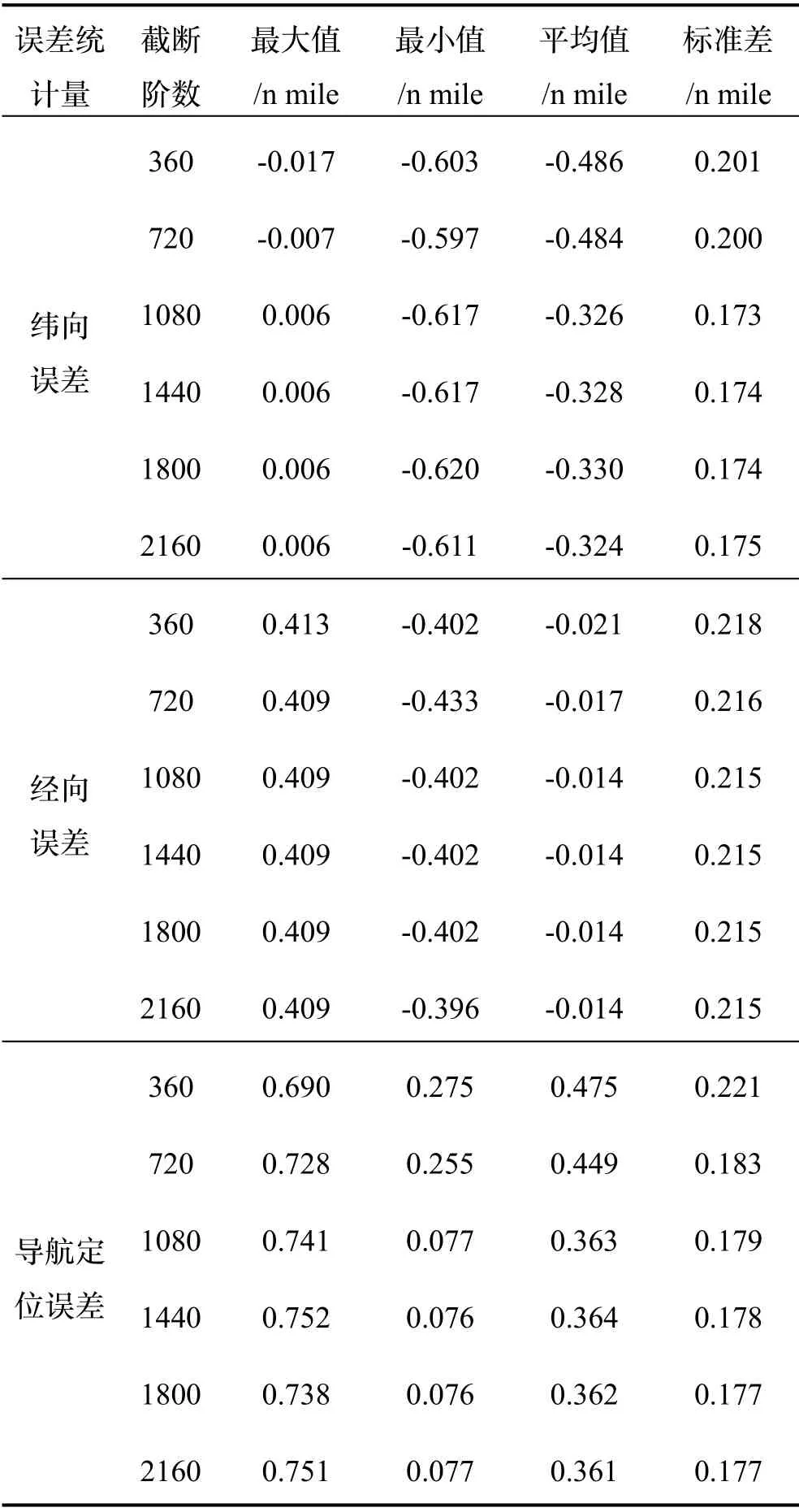
表3 误差统计Tab.3 Error statistics

由表3与图5结合可知，使用360至2160阶地球重力场模型进行随机线性化的EKF-mx匹配算法精度均优于EKF-9d与EKF-s2，匹配精度相较于INS均提高了61.3%以上，相较于EKF-9d和EKF-s2分别提高了18.7%和12.6%以上。匹配精度会随截断阶数的升高而提高，360~1080阶之间，截断阶数的提高可以有效提升匹配精度；而1080阶以上，截断阶数的增加对计算精度的提升效果较弱，因此选用1080阶地球重力场模型能够更好地兼顾匹配精度和实时性。

3.2 EKF不同线性化方法匹配效果分析

在试验区域内以航迹2为实验对象，分别使用九点拟合法（EKF-9d）、双二次曲面拟合法（EKF-s2）以及本文所提地球重力场模型法（EKF-mx）对重力异常与重力梯度进行随机线性化，模型计算至1080阶。计算并统计纯惯性导航（INS）、EKF-9d、EKF-s2与EKF-mx相较于参考位置的纬向误差Δy、经向误差Δx 以及导航定位误差航迹2航行24 h，初始误差设置为0.9 n mile，重力匹配校正479次，对重力匹配校正位置的误差进行统计，结果如表4所示，误差曲线如图6所示。

表4 误差统计Tab.4 Error statistics

图6 航迹与误差曲线Fig.6 Track and error curve

由表4与图6可知，24 h航行过程中，INS导航定位误差绝对值最大达到7.656 n mile，使用重力、重力梯度EKF匹配算法后，导航定位误差最大值减少了65.1%以上，导航定位精度提高了72.2%以上。使用EKF-mx匹配算法的导航定位误差控制在1.215 n mile以内，平均值0.527 n mile，相较于EKF-9d和EKF-s2算法，导航定位误差平均值分别减少了56.2%和48.2%，定位精度分别提高了55.3%和37.5%，充分证明了利用EKF-mx匹配算法可以有效减小INS累积误差，提高匹配精度。

4 结论与讨论

本文针对惯性/重力/重力梯度组合导航EKF算法中由于随机线性化误差而造成的线性化模型不准确引起滤波发散的问题，利用重力、重力梯度固有属性，提出了基于地球重力场球谐模型的随机线性化方法，并利用并行计算提高其计算效率，满足滤波实时性需求。经实验计算分析表明：（1）所提并行计算方案可以有效提高重力、重力梯度线性化过程计算效率，各个阶次模型线性化计算加速比均达到10倍以上，有效提高了计算的实时性。计算至1080阶的地球重力场模型以兼顾导航定位精度和计算实时性，线性化耗时优于0.02 s。（2）利用所提重力场模型线性化方法进行EKF-mx滤波匹配，在24 h航行过程中，相较于INS系统导航定位精度提高了87.6%，相较于使用九点拟合法的EKF-9d和使用双二次曲面拟合法的EKF-s2匹配算法导航定位精度分别提高了55.3%和37.5%，可以有效控制随机线性化误差，提高滤波精度。