浅谈无理数的几种证明方法

◎何 铭

(广东省广州市广东实验中学附属天河学校,广东 广州 510650)

一、用数论方法判别无理数

(一)用奇偶分析法证明：及(k为奇数)为无理数

以2为模,整数可以分成两类：被2除余1的数及被2整除的数,即奇数与偶数利用奇数与偶数的分类及其特殊性质,可以简便地求解、求证一些与整数有关的问题,通常我们把这种通过分析整数的奇偶性来解决所遇到问题的方法称作奇偶分析法

且和互质,即、最大公约数为1

可化成2=

这个式子左端2是偶数,所以式子右端也会是偶数又因为有：奇数×奇数=奇数,偶数×偶数=偶数,所以会是一个偶数不妨设=2,代入2=中得到2=4,两边同时约去2之后得到=2这里可以推出也会是一个偶数、均为偶数与、最大公约数为1矛盾,故假设不成立,原命题得证

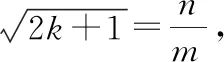
这里和互质,即、最大公约数为1

可化成(2+1)=

移项变形后可得：2=-,2=(+)(-),

可得知上式左端2为偶数,所以右端(+)(-)必为偶数则+或-为偶数说明、同为偶数或者同为奇数

若、同为偶数,则与，最大公约数为1矛盾

若、同为奇数,则为奇数,因为亦为奇数,所以2的素因数中有且仅有一个2,也就是说式子左端有且仅有一个2素因数再看式子的右端,因为、同为奇数,所以+、-同为偶数,也就是说(+)(-)的素因数中至少有两个2,也就是说式子右端至少有两个2素因数根据算术基本定理(素因数唯一分解定理) 可知：式子左端所含素因数与式子右端所含素因数要完全相同,与结论矛盾

综上所述,原假设不成立,命题得证

(二)用素因数分析法证明为(n∈N,且n不为平方数)为无理数

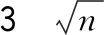
这里和互质,即、最大公约数为1

可化成=

将、、素因数分解可得：

=…,

=…,

=…,

因为不为平方数,、为平方数,所以有、、…、不全为偶数、、、…、以及、、…、全为偶数

若将素因数分解可得：

=…·…=…,

根据同底数幂相乘的法则：·=+,因为、、…、不全为偶数而且、、…、全为偶数所以、、…、不全为偶数所以≠,

与假设矛盾,原命题得证

(三)用最小数原理证明

则2->0、->0,

且-<,

故假设不成立,原命题得证

二、用麦克劳林级数判别无理数

利用麦克劳林级数,我们可以将一些数值代入可以展开成幂级数的函数中,得到一些无理数的无穷级数形式把无理数表示成无穷级数的形式,为判别无理数开拓了新的道路

(一)证明且n≠0)为无理数

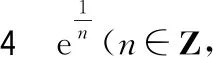
先证为正整数即>0的情况

令()=e,可得()=e的麦克劳林级数：

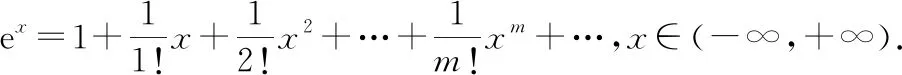
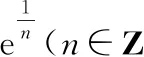
则有

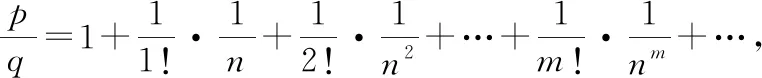
式子右同时乘!,得

式子左右同时乘,得

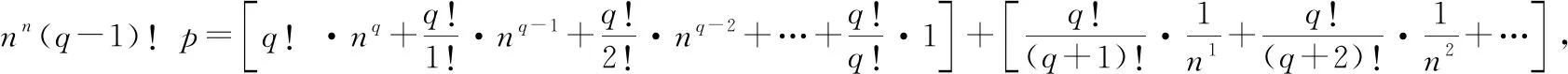
其中

根据等比级数求和公式

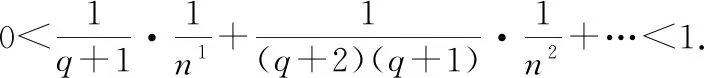
现在可知

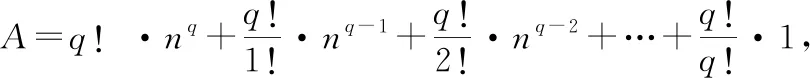
为整数,为小数

(-1)!=+,

上式左端为整数,右端不为整数，故矛盾

再证<0的情况令=-,∈且>0

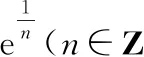
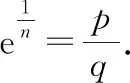
特别的,当=1时我们证明了自然常数e为无理数

(二)证明且n≠0)为无理数

先证为正整数即>0的情况

令()=sin,可得()=sin的麦克劳林级数：

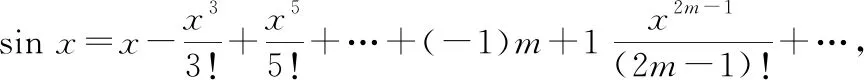
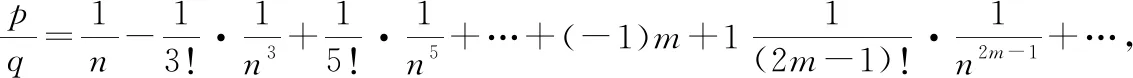
令为大于的一个某个奇数,上式左右两边同时乘!·得：

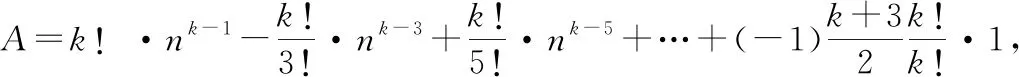
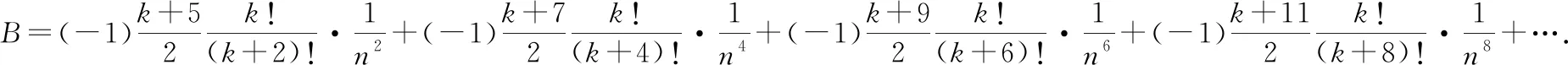
有

即有：||<1

其中

……

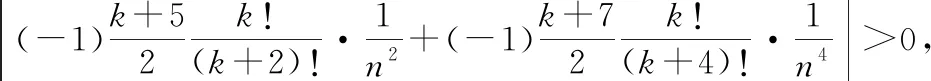
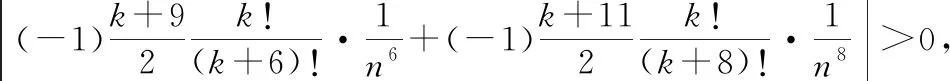
每一个中括号的结果符号相同,且绝对值大于0,所以||>0

综上所述：0<||<1

·(-1)·…·(+1)·(-1)·(-2)·…·2·1·=+,

为整数,为小数,上式左端为整数,右端不为整数矛盾

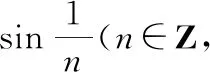
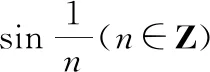
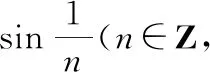
三、用多项式相关定理判别无理数

(一)利用艾森斯坦(Eisenstein)判别法证明

整系数多项式在有理数域上是否可约是与整系数多项式方程在有理数域上是否存在有理根这个命题是等价的所以我们可以通过把一些数看成某个整系数多项式方程的根,然后判断该整系数多项式在有理数域上是否可约从而判定这个数是有理数还是无理数艾森斯坦(Eisenstein)判别法就是其中的方法之一

应用艾森斯坦判别法证明无理数,关键是通过对多项式各项系数的仔细考察,设法找到合乎艾森斯坦判别法条件的素数通过寻找满足以上三个条件的素数,我们就可以找到方法判定无理数

先证明为整数的情况

在这个整系数多项式中,最高次项系数为=1,常数项为=-…,其余各项系数均为0

取素数=(1≤≤)满足：

(1)最高次项=1不能被=整除；

(2)其余各项的系数都能被=整除；

(3)常数项=-…不能被=整除

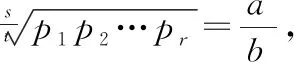
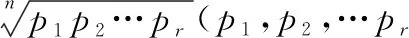
(二)利用整系数多项式有理根定理证明

从上文可以看出,艾森斯坦(Eisenstein)判别法是有一定局限的,而整系数多项式有理根定理条件就相比开放一些我们也可以利用这个定理来对无理数进行判定

在这个整系数在这个整系数多项式中,最高次项系数为=1,常数项为=-

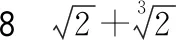
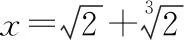
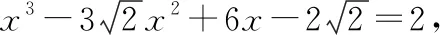
两边平方后,得：+12+36=18+24+8,

移项得：-6+12-8=0

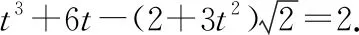
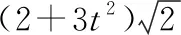
有理数-无理数=有理数,矛盾故原命题得证

3证明sin 10°为无理数

9sin 10°为无理数

将=10°代入隶莫弗公式(cos+sin)=cos+sin得(cos 10°+sin 10°)=cos 30°+sin 30°

化简得：(cos 10°+sin 10°)(cos10°-sin10°+2cos 10°sin 10°)=cos 30°+sin 30°,(4cos10°-3cos 10°)+(-4sin10°+3sin 10°)=cos 30°+sin 30°,

得到：4cos10°-3cos 10°=cos 30°,-4sin10°+3sin 10°=sin 30°

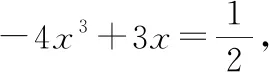
可化得：7-6-1=0

令()=7-6-1

所以有一些无理数看上去并非代数数,但只要细心挖掘一下就可以得到其实为一个整系数多项式方程的根,也是可以用整系数多项式有理根定理来判别的