用于四旋翼无人机姿态的改进遗传算法优化LQR控制

梁子斌，李擎

(1.北京信息科技大学 自动化学院，北京 100192；2.北京信息科技大学 高动态导航技术北京市重点实验室，北京 100101；3.北京信息科技大学 现代测控技术教育部重点实验室，北京 100192)

0 引言

四旋翼无人机具有垂直起降、自由悬停、飞行灵活等特点，现已被应用于高空航拍、资源勘探、抢险救灾等多个领域，具有良好的发展前景。但因其多输入、欠驱动、强耦合的特性，在复杂环境下，抗干扰的高精度姿态控制系统设计一直是理论研究的难题。

Elkhatem等[1]提出了一种鲁棒线性二次型(linear quadratic regulator,LQR)控制器和LQR—比例积分(proportional integral，PI)控制器用于无人机的位置姿态跟踪，两种控制策略都能使四转子稳定在期望的位置和姿态，具有更好的性能和鲁棒性。杨旭等[2]提出了一种自耦比例积分微分(proportional-integral-derivative，PID)控制器，用于四旋翼无人机的姿态控制，在Matlab/Simulink中通过仿真实验验证了所提出算法的有效性，姿态控制超调量最好时可控制在6%左右。Phinguyen等[3]针对外界干扰情况下的滑模控制问题，提出了一种基于神经网络的自适应滑模控制器用于无人机的姿态控制，所提出控制方法性能良好，有很强的抗干扰能力和跟踪性能。

在控制器优化方面，目前已有如遗传算法[4]、粒子群算法[5]、模拟退火算法[6]、灰狼算法[7]等多种智能优化算法。遗传算法具有高度并行的特点，其不依赖于辅助信息，具有较强的全局搜索能力[4]。王旭等[8]提出了一种改进遗传算法优化PID控制器，通过对遗传算法进行优化，防止其进入局部最优解。胡志新等[9]利用改进遗传算法对反向传播(back propagation，BP)神经网络进行了优化，使得交叉率和变异率在规定范围内自适应调整，提高了遗传算法的搜索能力。晋春等[10]利用改进遗传算法用于温室环境的动态优化，引入工程经验对部分个体进行修正，提高了算法的寻优能力。

针对四旋翼无人机抗复杂干扰能力差的问题，本文采用LQR控制器进行控制，并对控制器优化环节提出一种全流程改进遗传算法，用于控制器中加权矩阵Q的寻优选取。为了验证所设计控制方法的抗复杂干扰性能，设计了抗风特性干扰实验，证明了本文提出的控制方法的有效性。

1 数学建模

四旋翼无人机实验平台由安装在万向节轴杆上的4个带有旋翼的电机提供飞行动力。其中，前侧、左侧和右侧3个电机驱动对应的旋翼来实现飞行仿真器的俯仰(pitch)运动，左右两个电机驱动相应的旋翼实现飞行仿真器的滚转(roll)运动，后侧电机控制尾部旋翼实现偏航(yaw)运动。

1.1 系统动力学模型

对四旋翼飞行仿真器可建立如图1所示三维坐标系[1]。图1中，Fr为右侧电机升力，Fl为左侧电机升力，Ff为前侧电机升力，Fb为后侧电机升力，四旋翼飞行仿真平台左右臂与X轴夹角为60°。

由于电机转动依靠电压驱动，电机升力为

F=k0U

(1)

式中：k0为电机升力比；U为电机电压。

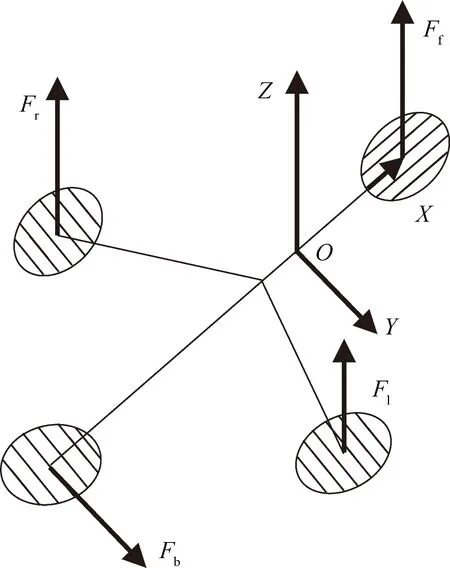
图1 三维坐标系四旋翼飞行仿真器

坐标原点位于万向节的支撑点，指向正前方电机的为X轴，垂直于X轴指向右侧的为Y轴，由左手定则确立坐标系的Z轴正方向。

定义前侧、左侧和右侧螺旋桨运动产生的力与Z轴正方向同向为正，后侧尾部螺旋桨运动产生的力与Y轴正方向同向为正。

为方便表示，做出如下假设：1)假设系统处于静止平衡状态，3个姿态角均为0，并忽略摩擦力、电机阻尼力矩等；2)忽略电机到达给定转速的时间；3)假设螺旋桨的输出风力为理想状态。

1.1.1 俯仰角方向运动模型

当四旋翼无人机实验平台静止时，俯仰角受力情况如图2所示。

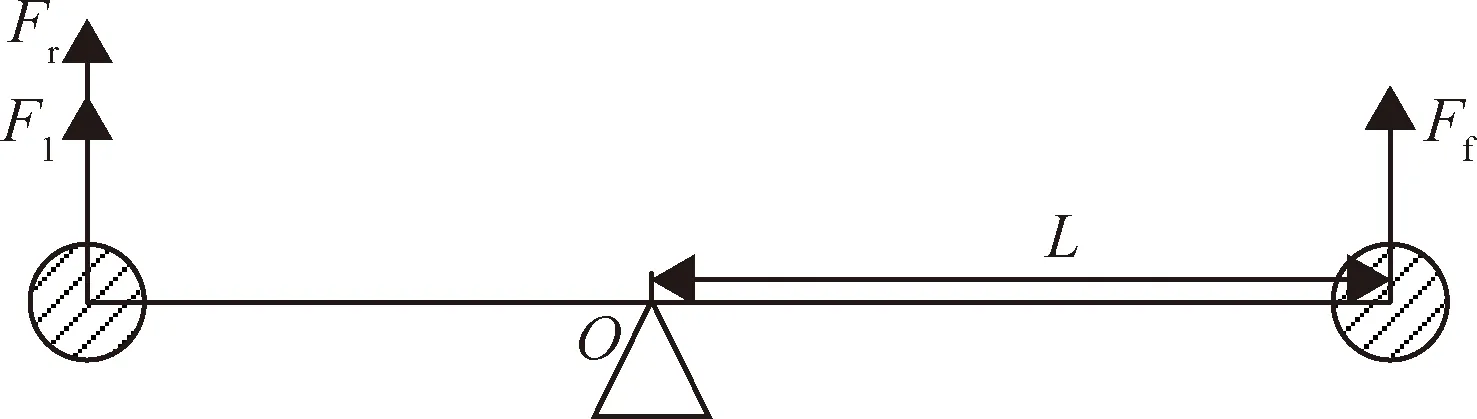
图2 俯仰角静止时受力分析

当实验平台左右电机产生向上的风力、前侧电机产生向下的风力时，定义俯仰角为正方向，建立方程：

(2)

将式(1)代入式(2)可整理为

(3)

式中：Ul为左侧电机电压；Ur为右侧电机电压；Uf为前侧电机电压。

1.1.2 滚转角方向运动模型

当实验平台静止时，滚转角受力情况如图3所示。

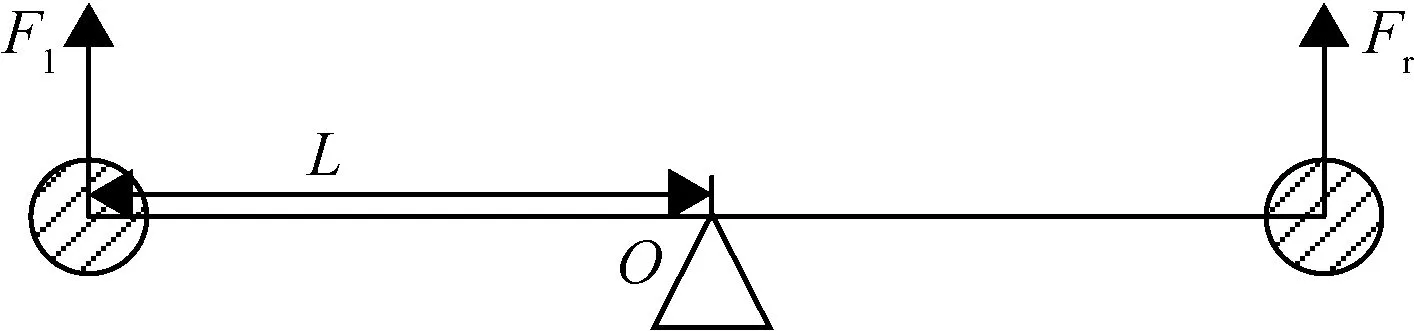
图3 滚转角静止时受力分析

当仿真器右侧电机向下运动时，定义滚转角为正方向。根据运动学公式，可建立方程：

(4)

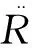
将式(1)代入式(4)整理可得：

(5)

1.1.3 偏航角方向运动模型

偏航运动仅由尾部电机控制，定义偏航角绕Z轴从上向下看顺时针运动为正方向，可建立方程：

(6)

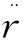
将式(1)代入式(6)整理可得：

(7)

式中Ub为后侧电机电压。

由于各个电机臂上配有电机罩等外部设备，将各个电机臂的质量近似视为一个质点，四旋翼无人机实验平台各物理参数如表1所示。

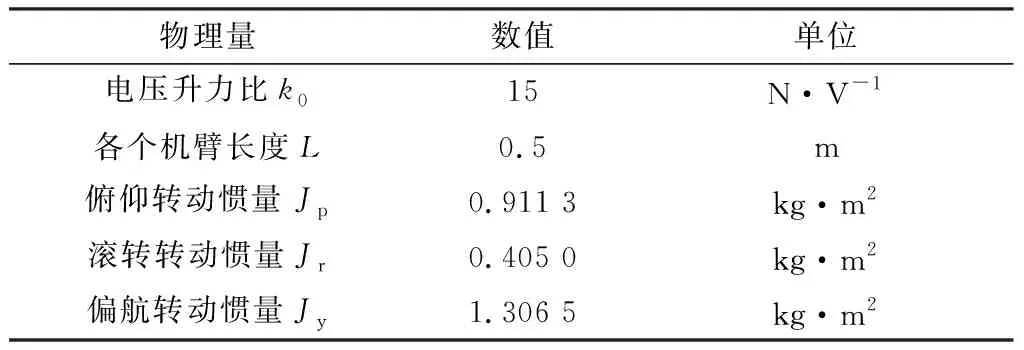
表1 四旋翼飞行仿真器物理参数

将表1数据代入式(3)、式(5)和式(7)，3个姿态角力矩平衡方程可整理为

(8)

1.2 系统状态方程

根据式(8)的力矩平衡方程，可建立状态空间方程：

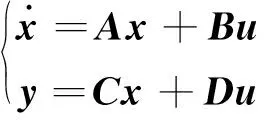
(9)

式中：

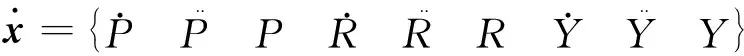
B=

D=0

1.3 风场模型

风力作用在四旋翼无人机体上的大小仅与风速有关：

(10)

式中：Fw为风作用力大小；Kw为风力系数；vw为风速。

1)阶段性风场模型

阶段性风指的是风速在某一阶段突然加强，在一段时间后逐渐减弱的一类风。本文采用文献[11]中的风场模型，来模拟阶段性风场扰动：

(11)

式中：vw为风速；vmax为风速最大值；T为阶段性风周期；t为时间；t′为风力作用开始时间。

2)全程性风场模型

全程性风是指风力一直作用在无人机体上，风力的大小随机性变化，与时间无关[11]，风速为：

vw=vmaxacos(ωt+φ)

(12)

式中：vmax为风速的最大值；a为(-1，1)的随机数；ω为风速波动宽度；φ为(0，2π)的随机变量。

2 LQR控制器设计

LQR是一种状态反馈控制器，多应用于多变量控制系统中[1,12]。

现假设有如下所示控制系统：

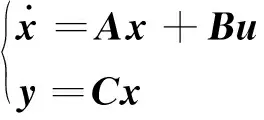
(13)

根据该状态方程，设计LQR控制器。定义LQR目标函数[13-14]：

(14)

式中x∈Rn×n;u∈Rn×m;Q为半正定矩阵，为状态变量的加权矩阵；R为正定矩阵。

设计状态反馈控制率为

u=-Klx

(15)

式中Kl为状态反馈增益矩阵。最优控制信号为

u=-R-1BTPx

(16)

式中P为正定对称常数矩阵，由Riccati方程得到：

(17)

由式(15)可得闭环状态方程：

(18)

2.1 单回路LQR控制器设计

本文采用LQR控制方法对四旋翼无人机的3个姿态角整体设计单回路控制器。根据四旋翼无人机实验平台状态空间表达式(9)，利用Matlab中的lqr()函数计算出Kl阵，其控制结构如图4所示。

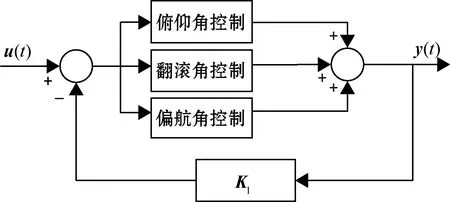
图4 单回路LQR控制模型

由于3个姿态角之间存在复杂耦合关系，单一回路的LQR控制器控制效果不佳，因此本文对3个姿态角进行解耦，分别设计控制器，进而实现多回路LQR控制器分别控制3个姿态角。

2.2 多回路LQR控制器设计

由于单回路LQR控制器依靠一个单一的状态反馈矩阵对系统进行控制，控制效果不佳，本文将俯仰、翻滚、偏航3个姿态控制量解耦分开控制，并设计相应的LQR控制器，使其可以单独控制，实现三回路LQR控制，即多回路LQR控制。

多回路LQR四旋翼姿态控制结构如图5所示。

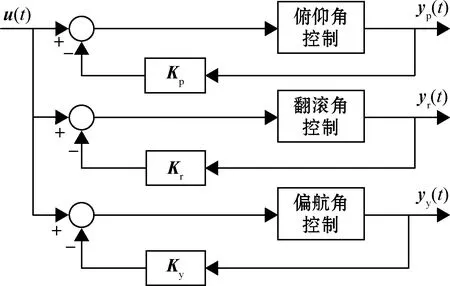
图5 多回路LQR四旋翼姿态控制结构

根据3个姿态角之间的耦合关系，现对其进行解耦，解耦后的俯仰角回路状态方程为

(19)

翻滚角回路状态方程为

(20)

偏航角回路状态方程为

(21)

根据式(19)～(21)的状态方程，分别设计LQR控制器，得到多回路LQR控制器。

2.3 控制器稳定性分析

根据李雅普诺夫(Lyapunov)理论对本文中所提出的控制器进行稳定性分析。

在本文中，很容易得出在x=0处为式(18)的一个平衡点。构造李雅普诺夫函数为二次型标量函数：

V(x)=xTPx

式(16)中P为正定矩阵，则有V(x)>0。

那么

(22)

将式(16)代入式(13)得：

(A-BR-1BTP)x

(23)

将式(17)和式(23)代入式(22)得：

xTP(A-BR-1BTP)x=

-xT(PBR-1BTP+Q)x

(24)

3 改进遗传算法优化LQR控制

遗传算法广泛应用于参数寻优等方面。针对传统的遗传算法易陷入局部最优解和过早成熟的问题，许多改进算法被提出，但大多集中在遗传算法的某单一环节的改进，搜索能力提升较小。本文针对四旋翼无人机LQR控制器提出全流程改进遗传算法(improved genetic algorithm，IGA)，扩大了遗传算法的搜索范围，将其用于优化LQR控制器，以提高控制性能。

3.1 Logistic混沌映射

混沌映射常被用于生成混沌序列，这是一种由简单的确定性系统产生的随机性序列[5]。在智能优化领域，由于其具有遍历性、随机性和非线性等特点，相比于传统的伪随机数生成，其随机性更强，遍历性更好。

本文利用Logistic混沌映射替代传统的伪随机数生成器生成均匀分布的初始化种群，其表达式为

zk+1=μzk(1-zk)

(25)

式中：z∈ [0,1]；μ∈ [0,4]，为Logistic参数。因为初始条件z0在Logistic映射作用下产生的序列是非周期的、不收敛的，故可用于随机种群的生成。

3.2 精英选择策略

本文采用有条件的精英保留策略，选择在本代适应度前10%的个体直接进入下一代，保护优良个体，在交叉和变异环节不被破坏，提高了遗传算法的搜索能力，剩余个体通过轮盘赌的方式进行选择操作。

轮盘赌选择[15]是根据个体适应度大小进行选择的一种方式，适应度越大，被选中的概率越大，其选择策略为

(26)

式中：pi为第i个个体被选中的概率；fi为第i个个体适应度；n为个体总数。

3.3 交叉环节改进

交叉环节影响算法的全局搜索能力。传统算法采用固定交叉率，在遗传过程中容易破坏优良个体，本文对交叉率进行自适应调节，利用Sigmoid函数平滑连续的特点，对该函数进行改造，提高算法搜索速度。

Sigmoid函数表达式为

式中：S(t)为Sigmoid函数；t为自变量。参考杨世忠等[4]提出的交叉率函数，并利用Sigmoid函数的特点，设计交叉函数：

式中：Pc为交叉率函数；Pc1为最大交叉率，取0.9；Pc2为最小交叉率，取0.4；fa为平均适应度；fmax为最大适应度；f为当前个体适应度。

3.4 变异环节改进

变异环节与算法的局部搜索能力相关。传统算法采用固定变异率，容易使遗传算法陷入局部最优解。本文引入了柯西分布理论，使变异率根据个体适应度大小进行自适应调节。

柯西分布的概率密度函数为

式中：x为自变量；x0为定义分布峰值位置的位置函数；γ为尺度参数。改进的变异率函数为：

式中：Pm为变异率函数；γ为尺度参数，取0.02；Pm1为最大变异率，取0.1。

在遗传算法迭代初期，变异率较小；随着迭代次数增加，在个体适应度小于种群平均适应度时，个体变异率最大，防止进入局部最优解；个体适应度大于等于种群平均适应度时，个体变异率较小，有利于保护优良个体不被破坏。

3.5 适应度函数

本文选取的遗传算法目标函数为：

式中：e(t)为系统误差；Mp为系统的超调量；ts为系统稳态时间，输出阶跃响应进入稳态值±Δ误差带范围内所对应的时刻，取Δ=5%；λ和τ为权重值。

超调量为

式中：ymax为输出最大值；y∞为系统无穷时刻的输出量。

在时间乘绝对误差积分准则的基础上，增加超调量和调节时间，并且根据系统的特点给予3个姿态角不同的权重值，有利于系统更好地满足设计需求。

由于遗传算法需要对每个个体进行适应度评价，个体适应度越大，控制效果越好，并且要求适应度数值应该是大于零的。由此选择目标函数的倒数作为适应度函数：

改进遗传算法的操作流程如图6所示。

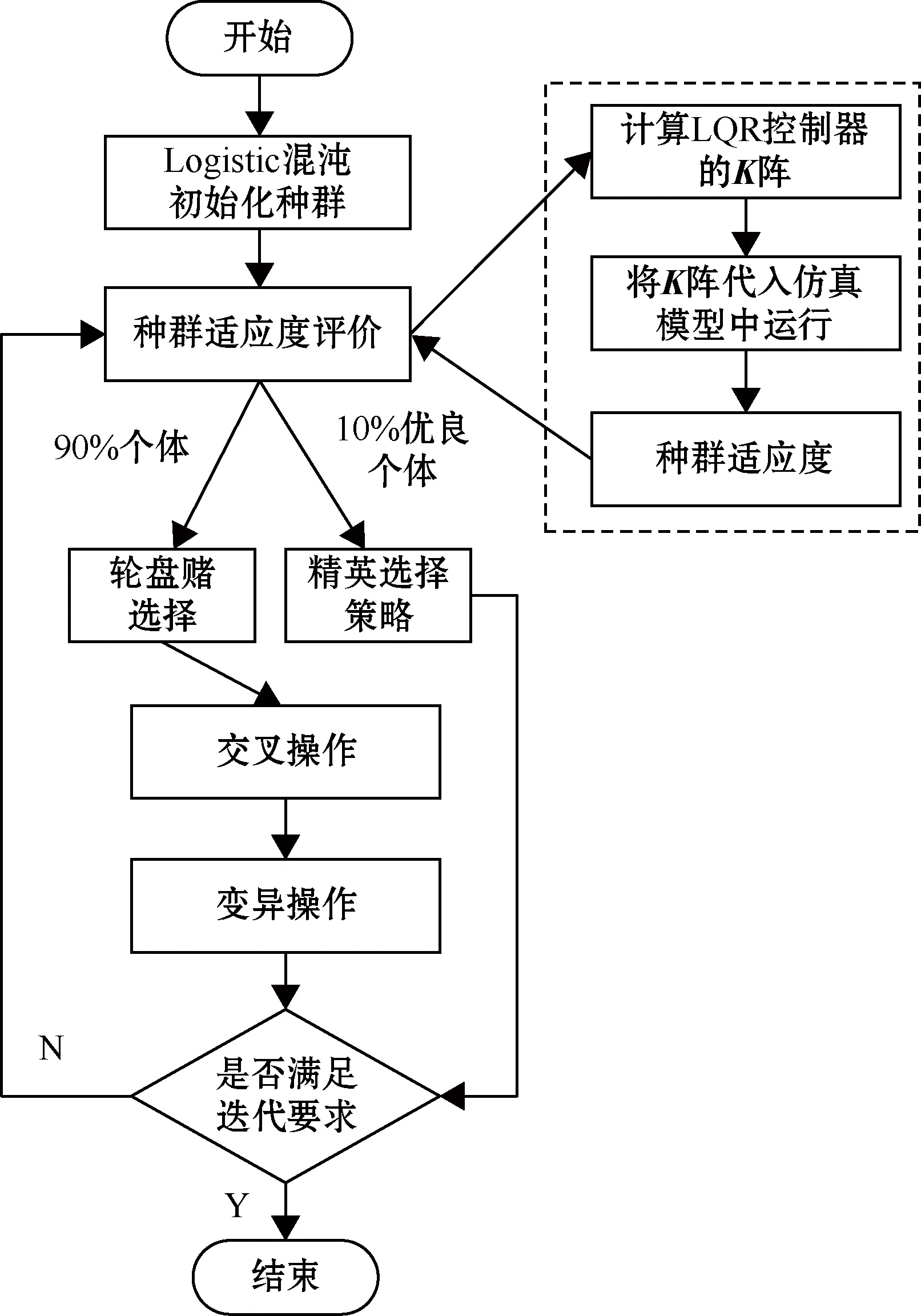
图6 改进遗传算法流程

4 实验

在Matlab/Simulink中，利用改进遗传算法优化单回路和多回路LQR控制器得到的无人机响应曲线与粒子群优化(particle swarm optimization，PSO)算法和模拟退火(simulated annealing，SA)算法优化得到结果进行对比，仿真结果如图7和图8所示。

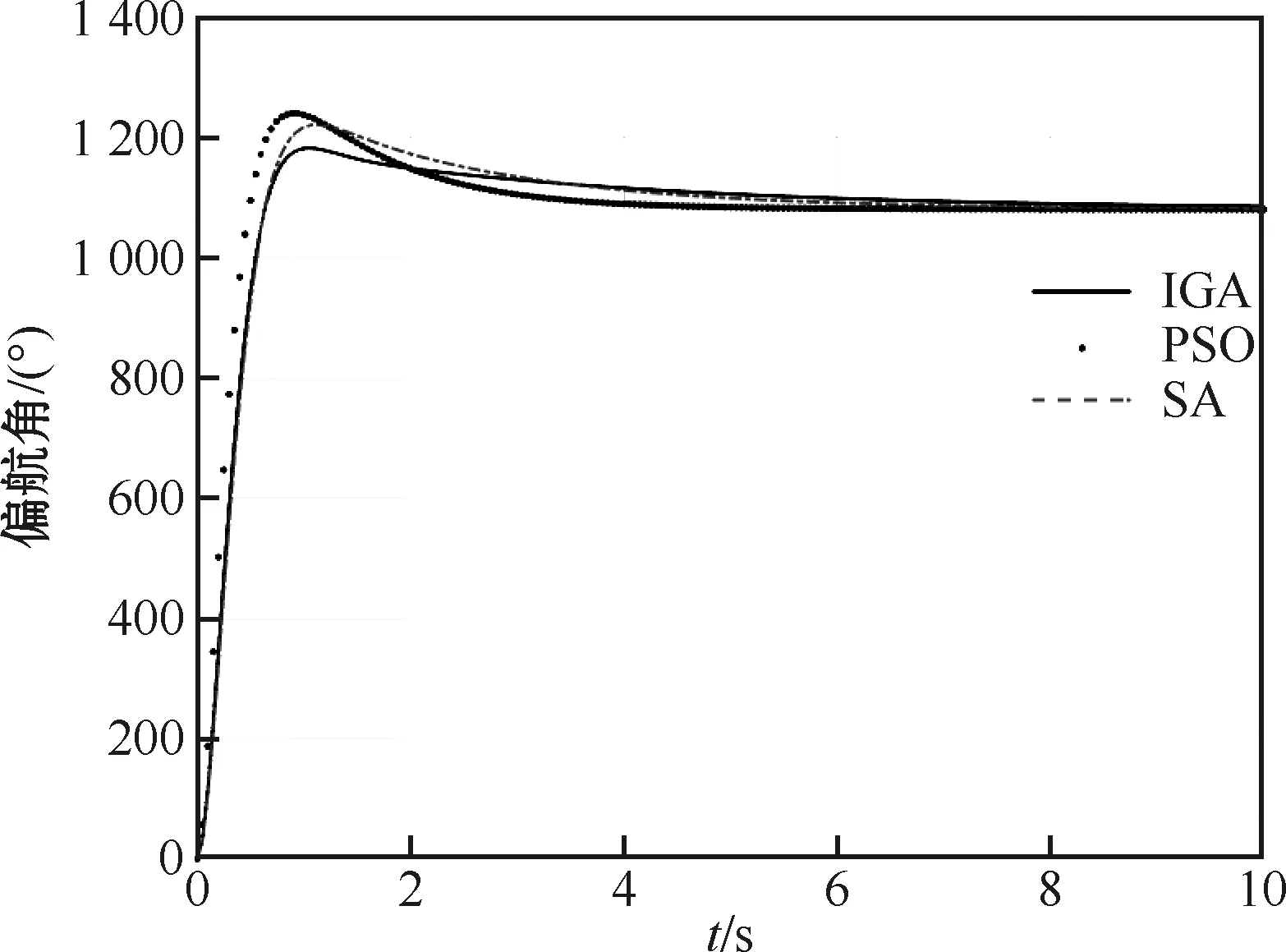
图7 单回路控制器偏航角响应曲线

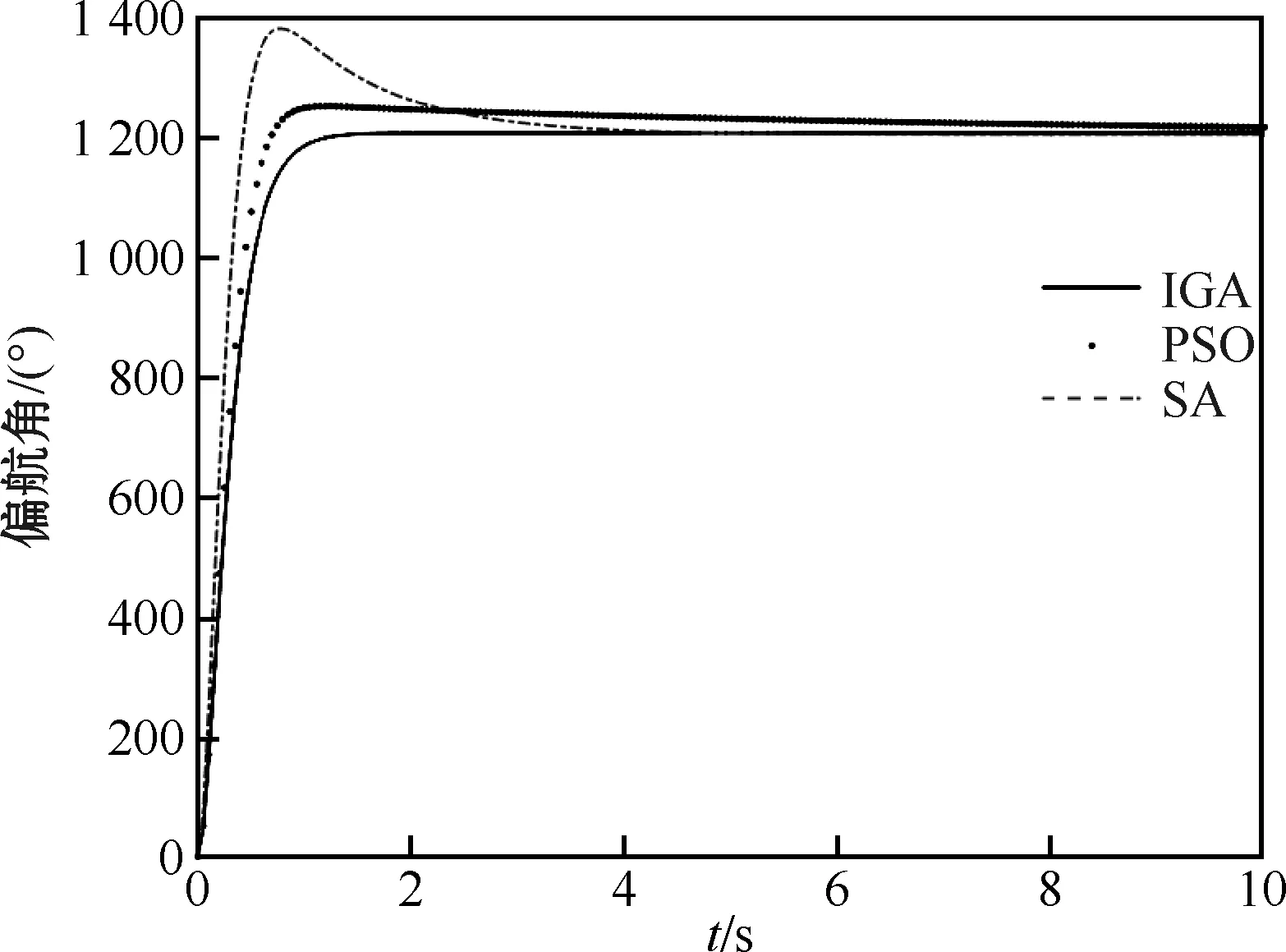
图8 多回路控制器偏航角响应曲线

IGA设置染色体个数为1，染色体长度为17，种群规模为100，Logistic参数为4，Pc1取0.9，Pc2取0.4，Pm1取0.1。

设计抗干扰实验验证所提出控制器抗风干扰能力，分别对单回路和多回路LQR控制器施加两种不同风干扰，即阶段性风和全程性风，所施加风力如图9和图11所示，控制器仿真响应曲线如图10和图12所示。

4.1 单回路控制器响应实验

此处仅以偏航角为例进行说明。图7为偏航角响应曲线，可以看出，IGA在单回路LQR控制器参数优化上具有良好的效果。

实验表明，利用IGA优化的控制器得到的调节时间为2.75 s，超调量为9.41%，动态响应更快，控制效果明显优于其他两种方法。

4.2 多回路控制器响应实验

图8为偏航角响应曲线，可以看出，本文所提出的IGA在多回路LQR控制器优化中，具有良好的优化效果，多回路LQR控制器相比于单回路LQR控制器，控制效果更好，系统响应更优良。

实验数据表明，IGA得到控制器的调节时间为0.8 s，超调量为0.24%，控制效果优良，明显超过另外两种优化方法，并且优于单回路LQR控制器的控制效果。

4.3 抗扰动实验

经过动态响应实验对比可知，设计的改进遗传算法优化LQR控制的性能最好。考虑到四旋翼无人机在实际场景应用中易受风的干扰，因此设计实验检验所设计单回路和多回路LQR控制器的抗风特性。

1)阶段性风抗风干扰实验

对实验平台施加式(11)的阶段性风，风力与时间的关系如图9所示，3个姿态角的动态响应如图10所示。

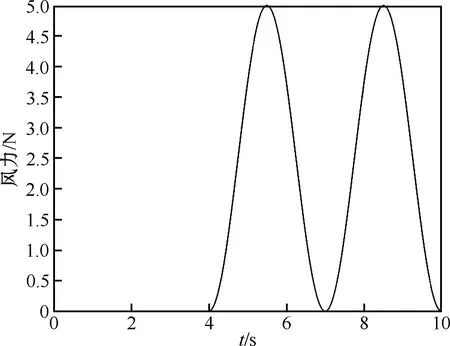
图9 阶段性风干扰

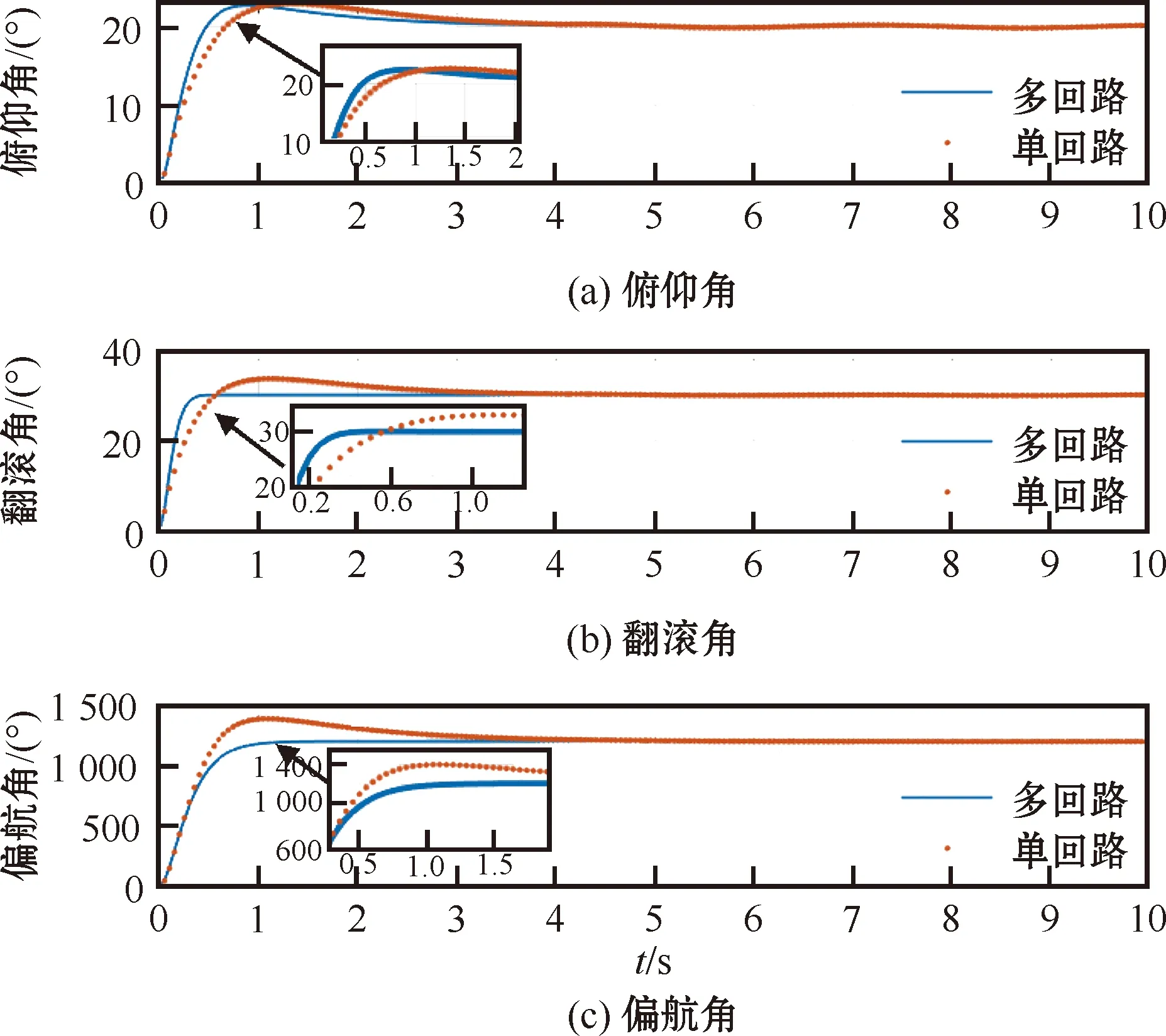
图10 阶段性风干扰下的响应曲线

从图10中可以看出多回路控制器在阶段性风抗风实验中，动态响应更快，更易进入稳态。

2)全程性风抗风干扰实验

对实验平台施加式(12)的全程性风，风力与时间的关系如图11所示，3个姿态角的动态响应如图12所示。

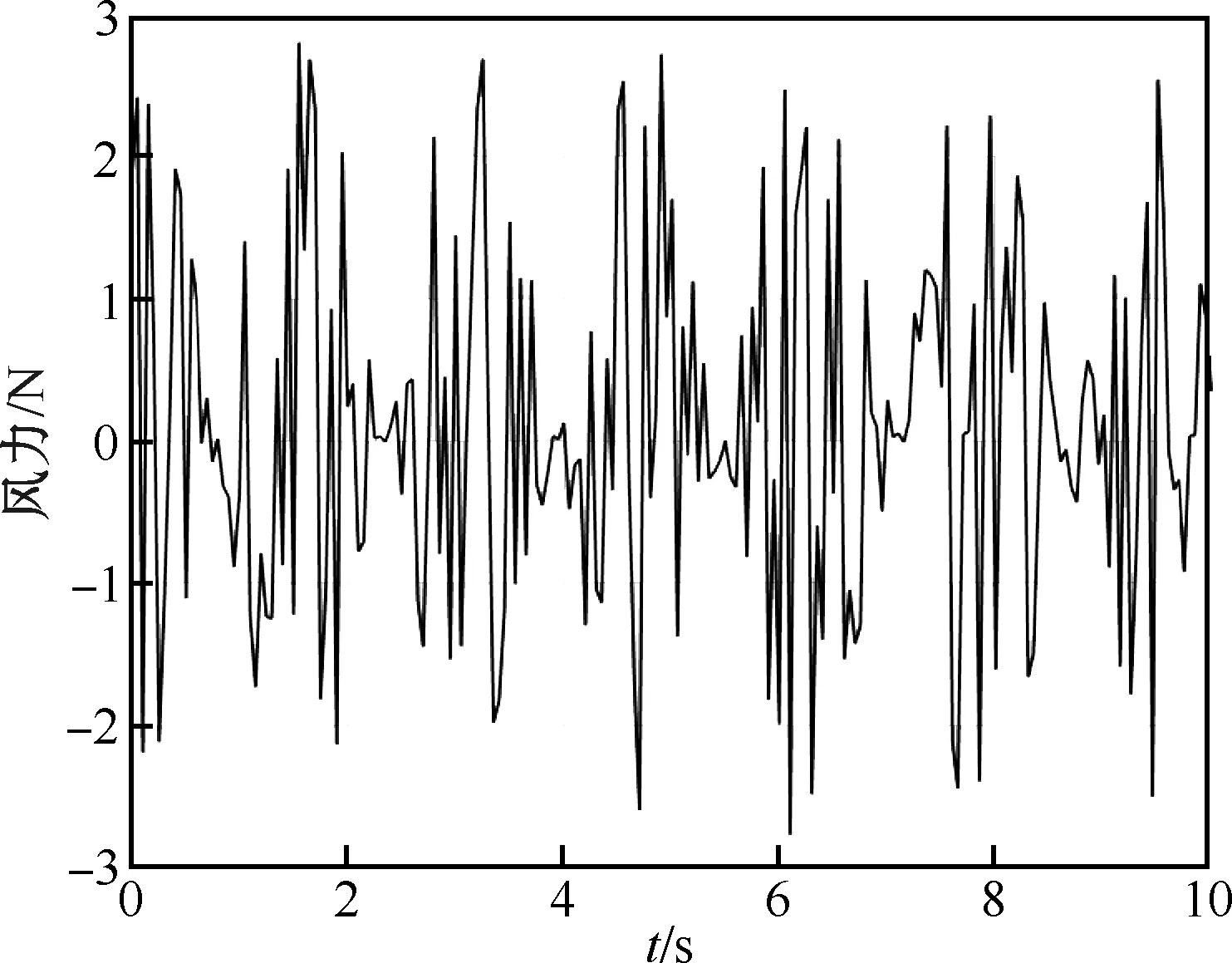
图11 全程性风干扰

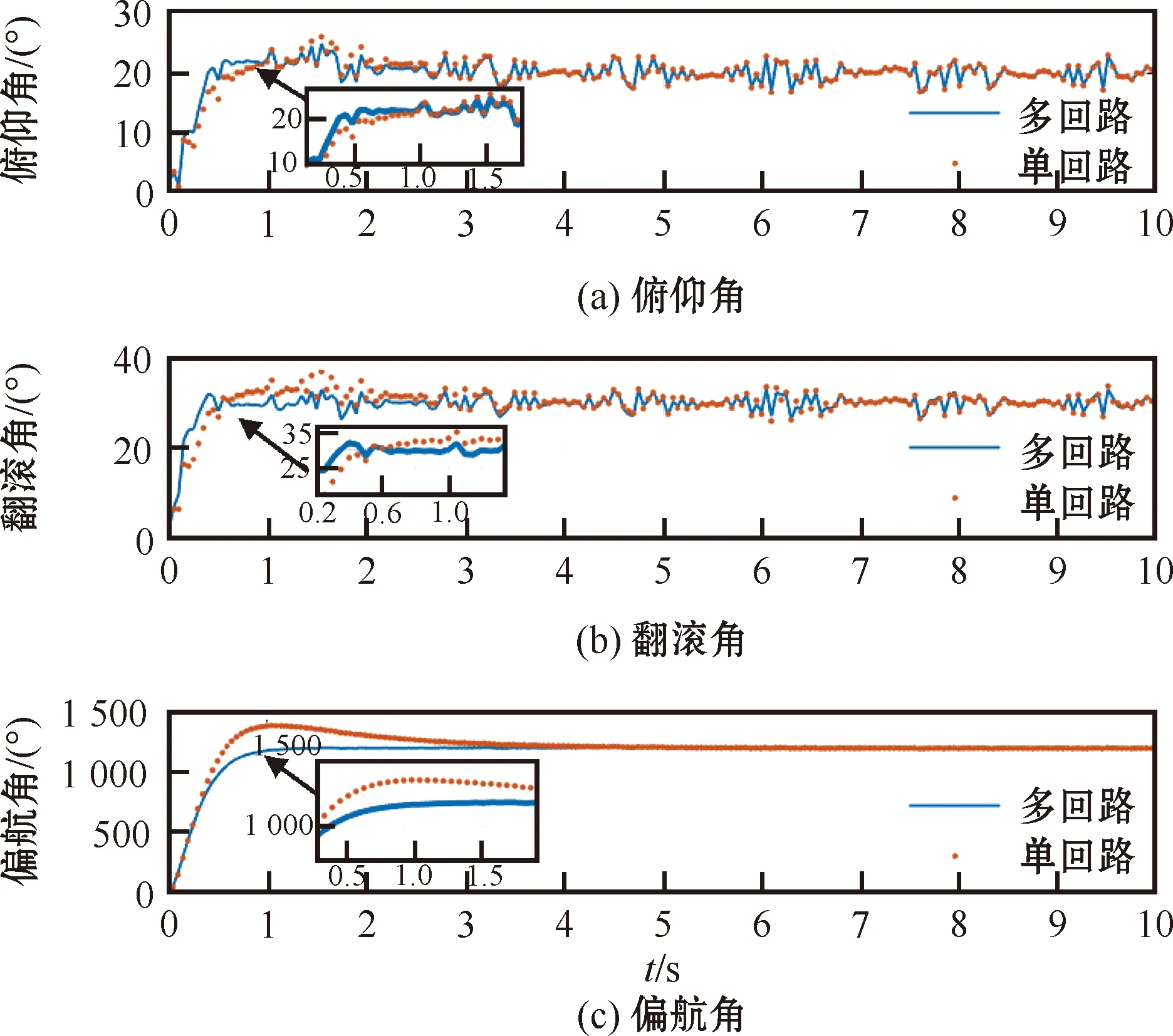
图12 全程性风干扰下的响应曲线

从图中可以看出，多回路LQR控制器在全程性风干扰的实验中，抗风特性效果明显优于单回路LQR控制器，其受到全程性风干扰时，更快进入稳态，响应速度更快。

由上述多种类多组实验可知：本文所设计的IGA优化LQR的多回路控制器的控制性能优，抗风特性好。

5 结束语

本文针对四旋翼无人机抗复杂干扰问题能力差的问题，采用LQR控制器对其3个姿态角进行控制，设计了单回路控制器和多回路控制器，并提出了一种改进遗传算法对所设计的两种控制器进行参数优化。通过动态响应实验，对比了IGA、PSO和SA算法，验证了所提出改进遗传算法的有效性。设计了抗干扰实验，对单回路和多回路LQR控制器分别进行了阶段性风和全程性风的抗风干扰实验，验证了多回路LQR控制器在复杂干扰情况下的优良特性。