基于模糊故障树和贝叶斯的阻力伞危险性分析

谷雨轩 肖凯锐 倪彬

（空军勤务学院 江苏徐州 221000）

阻力伞是用来缩短飞机着陆或被迫中止起飞时滑跑距离的减速装置。救生装备是“飞行员最后一道生命安全防线”。目前，国内外研究成果也将定量分析的方法逐步运用到阻力伞可靠性分析、危险性分析等研究中。有研究［1-2］通过分析阻力伞系统的组成、工作原理、常见故障模式及故障原因，提出了改进建议，为机务人员在日常维护、周期定检、出现故障等时机快速排除阻力伞系统故障提供参考。故障树模型是工程中常用的危险性分析模型，有研究［3］针对阻力伞机构发生故障的问题，对阻力伞机构开展了功能危险性分析和故障树分析研究，得到阻力伞意外打开、阻力伞意外抛伞和阻力伞不能打开等6个主要故障模式。

1 阻力伞主要事故故障树的建立

1.1 阻力伞常见故障分析

通过对事故资料进行统计分析，可能发生的故障模式包括意外抛伞、意外打开、不能打开或放伞时间超过规定和支撑机构散架掉落［2］。阻力伞意外抛伞和意外打开引起的事故最为严重，意外打开会导致飞机失控，其中，意外抛伞曾导致飞机冲出跑道，飞机解体，造成Ⅰ级事故，应重点关注。阻力伞不能打开或放伞时间超过规定发生次数较多，一般造成Ⅲ级事故，但在特殊情况下，如飞机起落架机轮制动失灵，超速着陆或在潮湿、结冰等不利条件下着陆时，如果阻力伞不能打开，飞机不能有效减速，会引起灾难性事故的发生［3］。

1.2 建立阻力伞主要事故故障树

通过阻力伞典型事故分析，将阻力伞故障发生模式按照阻力伞的意外开伞、意外抛伞、延迟开伞、伞未打开、减速功能失效［4］5 种故障状态进行划分记为X1～X5，深入分析造成各个故障状态下发生故障的主要影响因素，建立故障树［5］如图1所示。

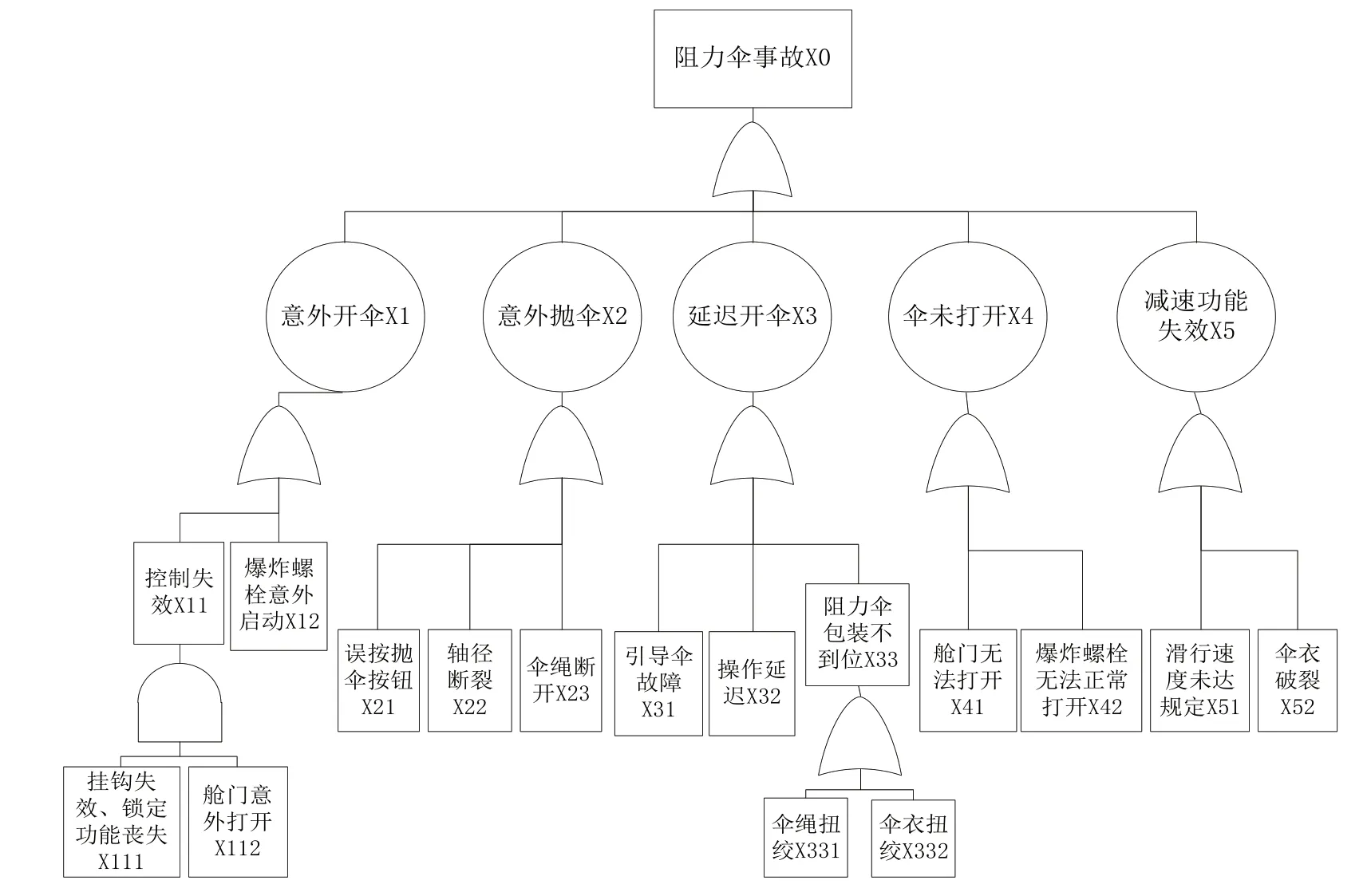
图1 阻力伞主要事故故障树

2 故障树定量分析

2.1 底事件模糊概率的确定

由于一些阻力伞故障因素在实际中缺乏数据累计和统计分析，而且事件本身无法用准确的概率来表达［6］，因此，本文采用模糊语言转化为模糊数的专家评判法计算此事件的概率。

通常描述时间概率的评估语言可以分为很小、小、较小、中等、较大、大、很大7个层次，用语言表示为VS、S、FS、M、FL、L、VL，每个评估语言对应不同的模糊区间及其隶属函数如图2 所示，阻力伞事故影响事件的失效概率数量级为10-3。

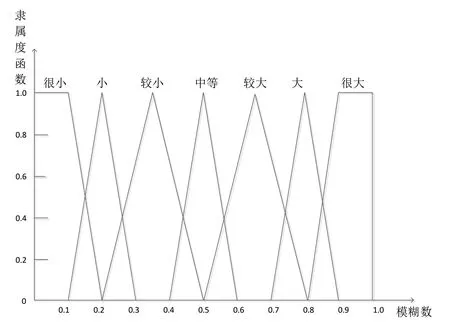
图2 评估语言对应不同的模糊区间及其隶属函数

对于某一事件的概率，可以根据10位专家作出的语言描述来得到该事件的模糊概率值，转化计算过程如下：

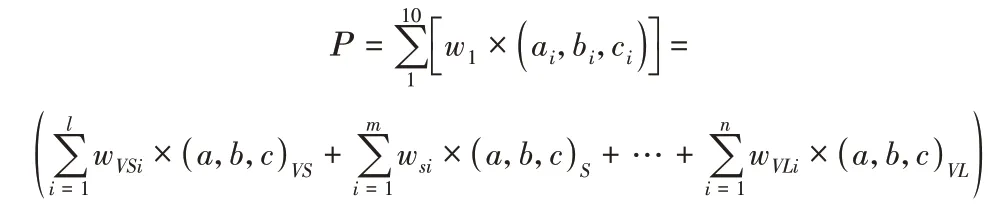
通过加权平均计算得出其模糊概率值为：

PX21=（0.1726，0.2933，0.4140）

用相同的方法，可以根据专家评估语言得出所有事件的模糊概率。

2.2 顶事件模糊概率的确定

如果一个中间事件包含多个底事件，在已知底事件模糊概率的条件下，中间事件发生的概率根据门算子进行计算，若与门包含n个底事件，引入与门算子和或门算子［7］。由底事件模糊概率可知中间事件的模糊概率如表1所示。

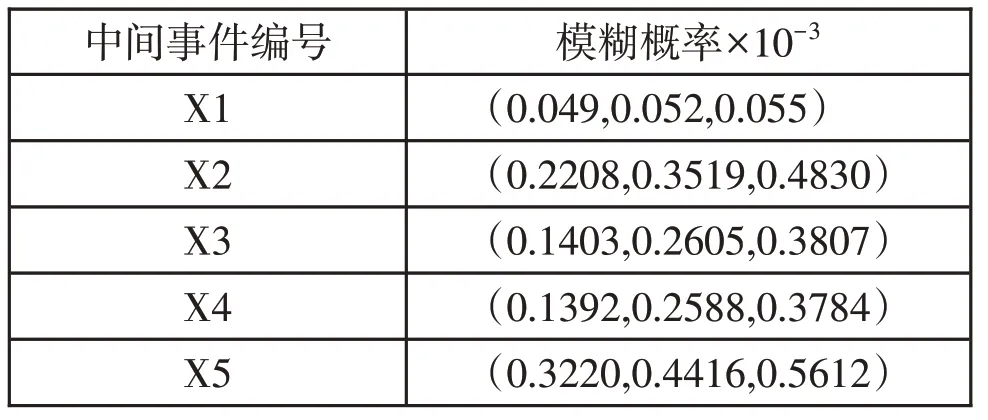
表1 中间事件的模糊概率

同理，可以求得顶事件阻力伞阻力伞故障X0模糊概率为：

PT=（0.628，0.812，0.917）×10-3

3 基于贝叶斯网络的阻力伞危险性分析

根据阻力伞主要事故故障树，得到转换后的贝叶斯网络如图3所示。

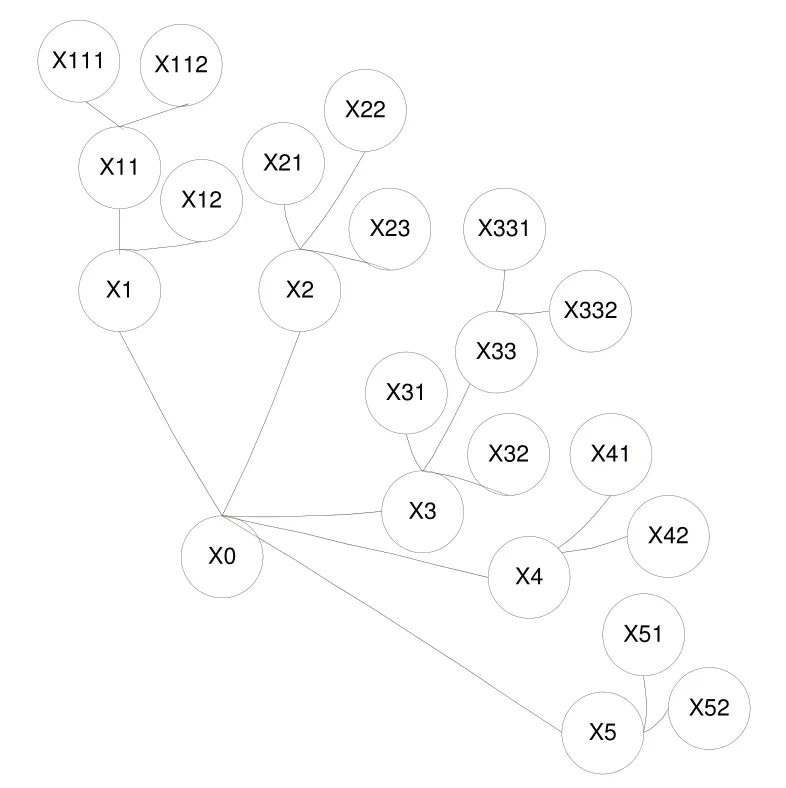
图3 阻力伞事故贝叶斯网络

根据已知的模糊概率，即根节点的先验概率，得到根节点的后验概率和概率重要度分别如表2所示。

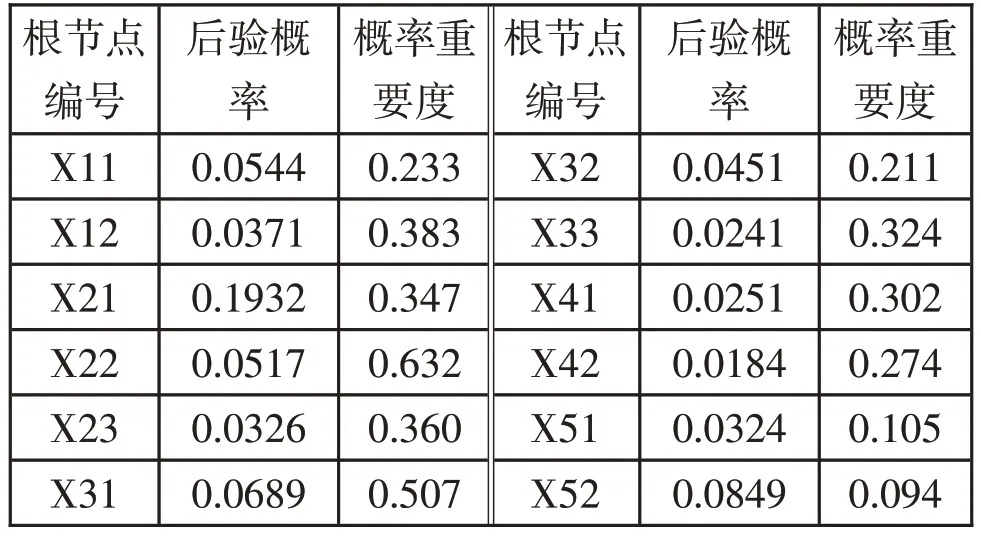
表2 根节点的后验概率和概率重要度

由根节点的后验概率可知，误按抛伞按钮X21、伞衣破裂X52、引导伞故障X31、控制失效X11、轴径断裂X22，但是根据概率重要度，其中伞衣破裂X52 对阻力伞工作影响较小，综合考虑后验概率和概率重要度，在进行排除故障时，应优先选择危险性较高的轴径断裂X22、误按抛伞按钮X21、引导伞故障X31，对阻力伞结构功能优化应考虑通过结构设计优化减少人为误按X21 和控制失效X11 发生的概率，以此来增加阻力伞的使用安全性。

4 结语

本文在阻力伞事故分析的基础上，通过模糊理论，确定底事件、中间事件和顶事件的模糊概率；利用贝叶斯网络，反向推理能力定量分析，提出轴径断裂、人为操作失误、引导伞故障事故危险性较高；通过结构设计，优化人员操作和控制系统具有的可行性，对于提升阻力伞使用安全性有一定的参考意义。