高速铁路轮轨噪声预测方法、特性规律及控制措施

圣小珍, 葛帅, 成功, 钟硕乔

（1.上海工程技术大学 城市轨道交通学院, 上海 201620；2.上海工程技术大学 上海市轨道交通振动与噪声控制技术工程研究中心, 上海 201620；3.华东交通大学 交通运输工程学院, 江西 南昌 330013）

0 引言

高速列车在运行过程中, 所有车体与车外空气接触的部分都与空气发生强度不同的相互作用, 同时, 列车还通过受电弓与弓网相互作用、通过轮对与轨道结构和下面的桥梁或路堤相互作用。这些相互作用, 导致气流状态变化以及车体与轨道等结构振动, 从而产生噪声。可以说, 高速列车车体表面的任何地方都是噪声源。除此以外, 列车本身装配的一些设备, 如空调系统、冷却风机、驱动电机和齿轮等, 也会产生噪声。在高速条件下, 这些设备噪声远低于上述相互作用产生的噪声。

因此, 高速列车的主要噪声源在车外, 噪声通过复杂路径和机理分别传入车内和传向车外。传入车内时, 乘客听到的噪声称为车内噪声。对于车内噪声, 噪声源是固定声源。传向车外时, 线路周围居民听到的噪声称为列车引起的环境噪声或列车通过噪声。对于列车通过噪声, 上述噪声源是高速移动的声源, 声源的马赫数较高（当列车速度为400 km/h即111 m/s时, 移动声源的马赫数是111/343=0.32）, 会产生显著的多普勒效应。

根据声源的发声机制, 噪声被区分为轮轨噪声、气动噪声和桥梁噪声。整个车体外表面都是气动噪声源, 但对列车通过噪声来说, 分布在转向架区域和车头区域的气动噪声源最重要, 因为这些部位的许多部件顶风横行, 其迎风面和两侧会产生强烈的压力脉动, 其尾部则产生各种尺度的漩涡脱落, 这些都是气动噪声产生的根本原因。高速列车噪声的第2个主要来源是轮对与钢轨的相互作用。轮对沿钢轨高速滚动时, 不可避免地产生高频相互动力作用, 导致轮对、钢轨和轨道板或轨枕产生振动, 从而辐射噪声, 这种噪声称为轮轨噪声。高速列车噪声的第3个来源是高架桥梁结构振动辐射的噪声, 称为高架桥梁结构噪声。我国高速铁路线路80%以上铺设在钢筋混凝土高架桥梁上, 列车高速通过时, 上述轮轨相互作用也会导致桥梁振动并辐射噪声。高架桥梁结构噪声的能量主要分布在200~250 Hz以下的频率范围内, 一般不会影响目前对高速铁路环境噪声的A计权评价。

到目前为止, 我国高速铁路最高运营速度为350 km/h, 400 km/h的高速列车正在研发中。高速列车运行速度提升势必加大列车与空气和轨道结构的相互作用, 加剧噪声的产生和传播, 进一步污染线路周边环境。因此, 高速铁路噪声是其发展和运维面临的关键问题之一。国家铁路局在《“十四五”铁路科技创新规划》中提出“推动更高速度轮轨技术研发, 深化高速列车振动与噪声控制基础理论研究, 开展列车在更高运营速度等级下的减振降噪技术研究, 提升列车高运营速度下的安全性、可靠性和舒适性。”

要控制列车通过噪声, 需要知道主要噪声源。研究表明[1］, 由于复兴号列车在气动设计上的先进性, 其在评价点的通过噪声在350 km/h的速度下, 依然是轮轨噪声为主。因此, 如果要进一步控制列车通过噪声, 必须优先控制轮轨噪声, 或者至少与控制气动噪声同等重要。为此需要进一步深入研究高速铁路轮轨噪声的发声机理、影响因素、预测方法、规律特性和控制措施。基于过去几年的研究工作, 对这几方面的研究成果及存在的问题从物理机制上进行介绍, 共包括5个方面的内容, 即轮轨发声机理和轮轨粗糙度、轮对声振特性、轨道结构声振特性、轮轨高速高频相互作用和轮轨噪声估算以及轮轨噪声控制措施。

1 轮轨发声机理和轮轨粗糙度

基于轮轨系统的列车, 通过轮对沿钢轨的滚动实现列车移动。由于车轮不是绝对圆的（或者说车轮具有粗糙度, 称为车轮粗糙度）, 钢轨顶面也不是绝对平顺（或者说钢轨顶面具有粗糙度, 称为钢轨粗糙度）, 所以当轮对沿钢轨滚动时, 会不可避免地引起车轮与钢轨的相对运动。因为轮对和轨道结构具有惯性和弹性, 轮轨的相对运动必然导致轮对和轨道结构的弹性变形和振动, 进而向空气中辐射噪声。这种噪声就是轮轨噪声, 其发声机理见图1。因此, 轮轨噪声的发声涉及轮轨粗糙度、轮对声振特性、轨道结构声振特性以及轮轨相互作用。无论是普速铁路还是高速铁路, 轮轨噪声发声机理一样, 然而, 在高速条件下, 轮对声振特性、轨道结构声振特性以及轮轨相互作用及其分析方法, 则特别需要考虑列车速度的影响。

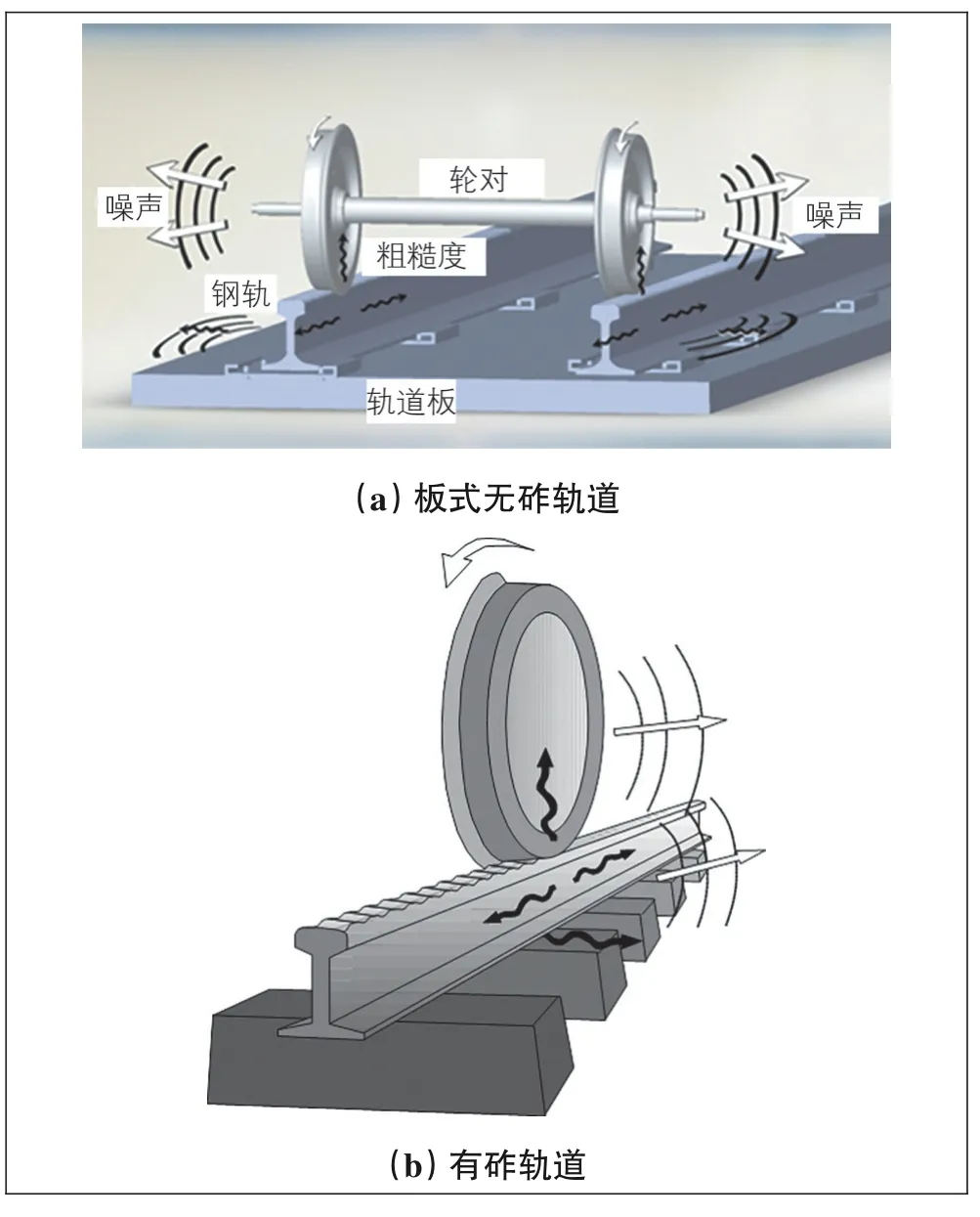
图1 轮轨发声机理

对轮轨噪声来说, 钢轨粗糙度通常指钢轨顶面名义滚动带上沿纵向的高低不平。纵向坐标为x处的钢轨粗糙度用z（x）表示, 通常是很不规则的随机函数（见图2）。图2中的尖峰可能由测试误差造成, 也可能由钢轨上的凹坑、焊接头等离散型不平顺造成, 需具体分析。用作轮轨噪声分析时, 一般不考虑这些尖峰。

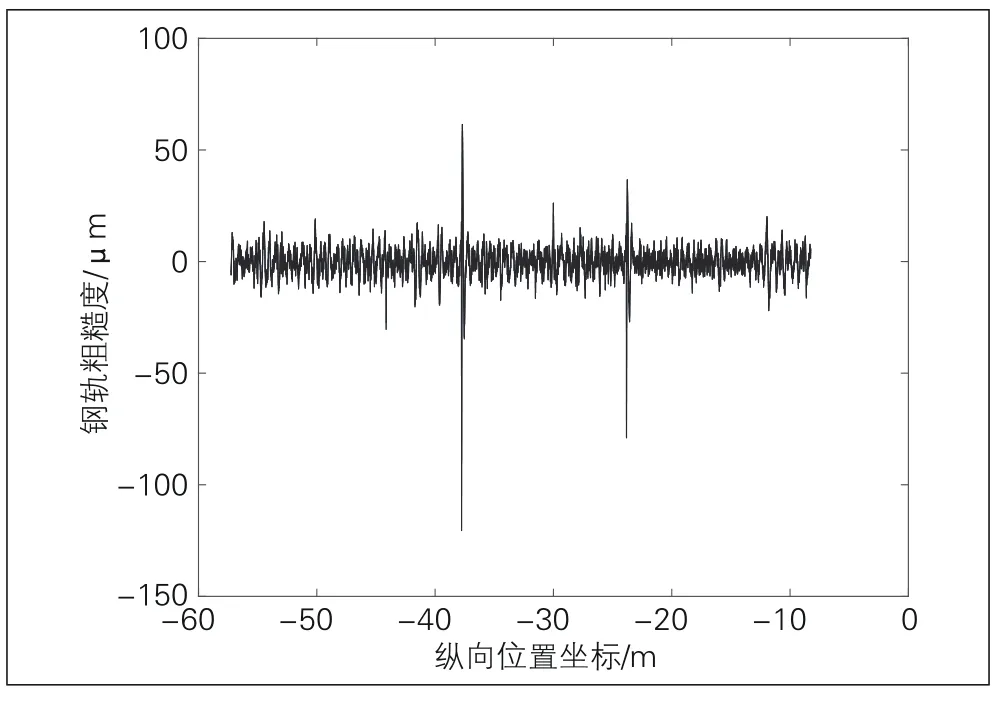
图2 钢轨粗糙度示例

尽管z（x）是随机函数, 但由于测试范围有限, 测试范围以外的钢轨粗糙度认为是重复的, 换句话说, 假定z（x）是周期函数。根据傅里叶级数原理,z（x）可以近似地表达为一系列正弦和余弦函数的和, 因此, 可以先假定钢轨的不平顺是1个单一波长λ且幅值为A的正弦函数, 即：

纯粹从几何上考虑, 车轮沿钢轨以速度c滚动时, 车轮中心将按下面的规律上下振动：

由于车轮具有惯性, 其要反抗式（2）所表示的上下振动, 所以在轮轨之间产生动态轮轨力。由于扣件对钢轨的离散支撑, 实际轮轨力中除了包含式（3）所示的频率成分外, 还包含其他频率成分。动态轮轨力将激发车轮和轨道结构的振动, 辐射轮轨噪声。把式（3）得到的频率称为波长为λ的粗糙度的激励频率, 简称钢轨粗糙度激励频率。

轮轨噪声需要考虑的频率约为50~5 000 Hz。频率再高, 从式（3）看出粗糙度的波长则很短, 短到比轮轨接触斑的尺寸还小。这类粗糙度将被压扁在接触斑内, 不能发挥太大的激励作用[2］。根据式（3）可知, 不同车速下需要考虑的粗糙度波长范围不同。对速度在250~400 km/h的高速列车, 需要考虑的粗糙度波长范围为0.02~2.22 m。即研究高速铁路轮轨噪声需准确测量波长为大约2 m以下的钢轨粗糙度。

如果车轮滚动圆不是绝对圆, 则其滚动半径不是常数, 而是环向角坐标θ的函数, 即R=R(θ)。显然, 这是以2π为周期的周期函数, 因此可以展开为傅里叶级数：

式中：R0是车轮的名义半径（平均半径）；Bnsin(nθ+φn)称为车轮的第n阶不圆度（或n阶多边形）,Bn是n阶多边形的幅值, 其与R0相比是很小的量,φ是初相位。当车轮中心往前移动1个距离x=ct+x0, 车轮转过的角度近似为θ=(ct+x0)/R0, 这时式（4）变成：

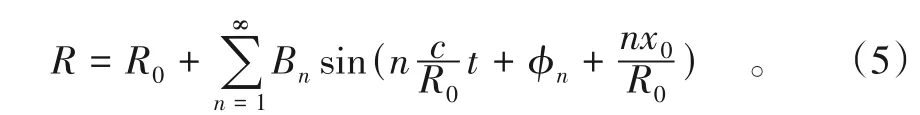
即如果钢轨固定不动, 则车轮中心将按式（5）作上下振动。式（5）表明, 车轮中心上下振动包含了一系列简谐振动（或说谐波）分量, 其中第n阶简谐振动的幅值为B, 频率为：

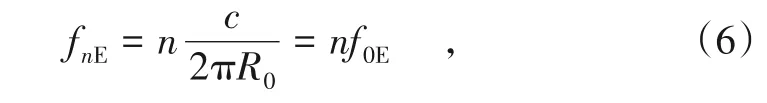
2 轮对声振特性

2.1 简谐轮轨力作用下轮对振动

轮对在与钢轨发生相互作用过程中, 转动、移动、振动并辐射噪声。在已知列车速度和车轮平均滚动半径时, 可认为轮对的转动速度和移动速度已知, 但其振动和声辐射则取决于轮对的声振特性和轮轨力。所谓轮对的声振特性, 是指轮对在给定的（通常是单位大小的）轮轨力激励下, 轮对振动和声辐射与激励频率间的关系。由于轮对和轮轨力一起向前移动, 因此, 在考虑轮对的振动时, 只须考虑轮对的旋转而无需考虑其移动。因此, 轮轨力的作用点在空间固定不动, 但相对轮对沿车轮的滚动圆旋转, 旋转轮对见图3。过去对普速铁路轮对的振动分析, 不考虑轮对的旋转, 因此可以应用常规的有限元法分析软件进行分析。当考虑轮对旋转后, 常规的有限元法分析软件不再可用。为此, 文献[3-4］建立了一套求解方法。因为轮对可以近似为轴对称体, 轮对的响应可以通过2维有限元模型求解, 计算旋转轮对在轮轨力作用下响应的2维有限元模型见图4。

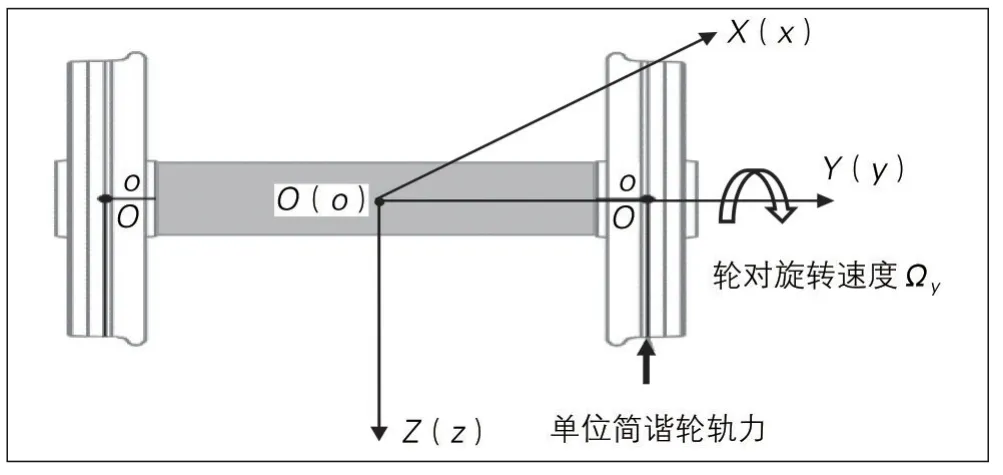
图3 旋转轮对

图4 计算旋转轮对在轮轨力作用下响应的2维有限元模型

轮对是有限尺寸弹性体, 具有模态特性（固有频率和振型）, 如果不旋转, 在简谐力作用下, 会在轮对的固有频率上发生共振。单位垂向简谐轮轨力作用下受力点的垂向响应（旋转对应车速300 km/h）见图5, 图5画出了某高速铁路轮对在右边轮轨接触点受到单位垂向简谐力作用时受力点在垂向的振动位移幅值与频率间的关系（实线）, 图中的峰值表明轮对在相应的固有频率上发生共振。共振峰的高度和尖锐度取决于轮对的材料阻尼, 阻尼越高, 共振峰高度越低。当轮对旋转时, 从车轮上看轮轨力沿滚动圆旋转（见图3）, 因此是移动荷载, 会产生移动荷载效应, 而且轮对旋转还会改变自身的自由振动（模态）特性, 使轮轨接触点（其现在不是轮对上的固定点, 而是空间中的固定点）的响应发生变化。研究表明[3-4］, 轮轨接触点的振动依然是简谐, 振动频率与轮轨力频率相同, 因此可以画出其振动幅值与频率间的关系曲线, 用来揭示旋转轮对的共振特性（见图5中的虚线）。可以看出, 当轮对旋转时, 轮轨接触点的共振响应不再发生在轮对原来（即不转时）的固有频率上, 而是发生在另外2个频率上, 这2个频率1个比原来的固有频率低, 1个比原来的固有频率高。这是旋转轮对共振频率的分叉现象。上下共振频率（指角频率）之差为2mΩy-Δω1-Δω2, 其中m为原有固有频率对应的模态节径数,Ωy为轮对的旋转角频率（或角速度）, Δω1和Δω2为旋转带来的固有频率绝对变化值（旋转使原有固有频率变成2个固有频率, 1个比原有固有频率大, 1个比原有固有频率小）。上下共振频率差可以近似计算为。对速度为300 km/h、半径为0.46 m的轮对, 旋转频率是28.85 Hz；对节径数为5的模态, 2个共振频率相差大约287 Hz。因此, 如果按照车轮不转的情况设计车轮降噪措施, 车轮旋转后, 降噪措施有效工作频率不一定靠近旋转轮对的共振频率。高速旋转轮对的振动控制措施是没得到充分研究的问题。

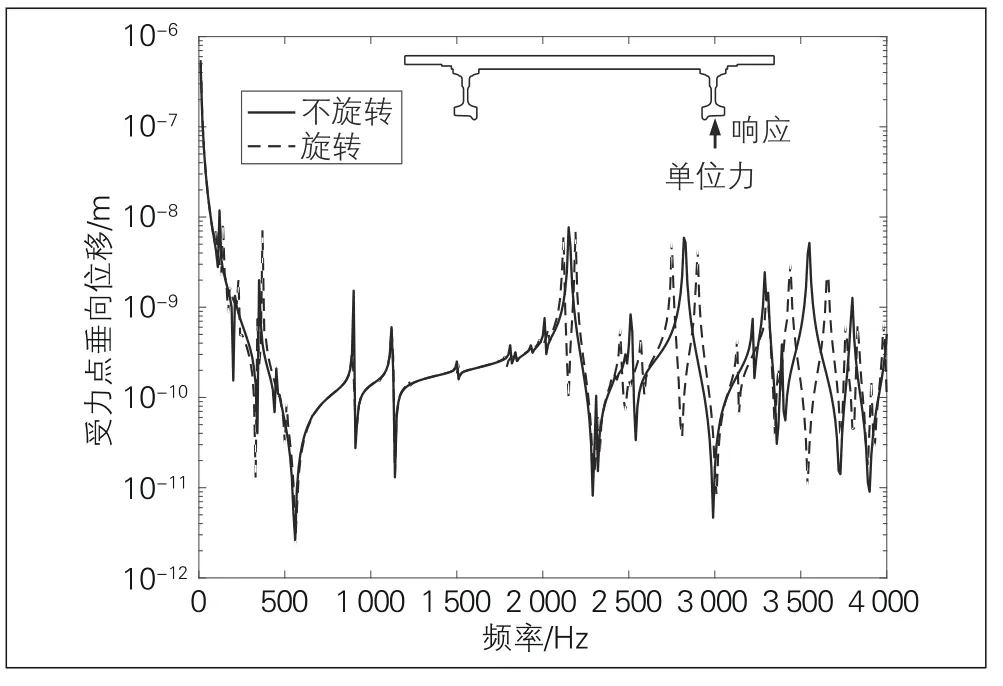
图5 单位垂向简谐轮轨力作用下受力点的垂向响应（旋转对应车速300 km/h）

图5基于自由轮对（即轮对不与任何其他结构联系）计算得到。由图5可知, 当频率高于约2 000 Hz时, 轮对模态非常丰富, 响应也很剧烈, 即轮对的声辐射在这个频段上高效率。图5也表明频率低于1 000 Hz时, 轮对也有一些模态（主要表现为车轴的弯曲）, 但由于实际轮对与一系悬挂系统相连, 一系悬挂减振器的阻尼以及轮对与轨道的横向相互作用将有效抑制这些模态响应。

静止轮对模态节径数反映了轴对称弹性体振动模态特征。如果1个模态的节径数为m, 表示按这个模态振动的轮对有m个过轴线的截面不振动。轮对模态见图6, 图6给出了节径数分别为4、5、6的3个轮对模态。当轮对旋转时, 原来（轮对不转时）节径数为4、5、6的3个轮对模态（可以看成是2个沿相反方向旋转的振动波的干涉结果）分解为2个沿相反方向旋转的波, 其中1个波的频率（其为旋转轮对的固有频率）比原来的固有频率低, 1个波的频率比原来的固有频率高, 出现固有频率分叉现象。从轮对观察, 轮轨力是移动荷载, 会产生多普勒效应, 使激发轮对振动的频率发生改变。当改变后的激励频率与旋转轮对的固有频率重合时, 轮对发生共振。

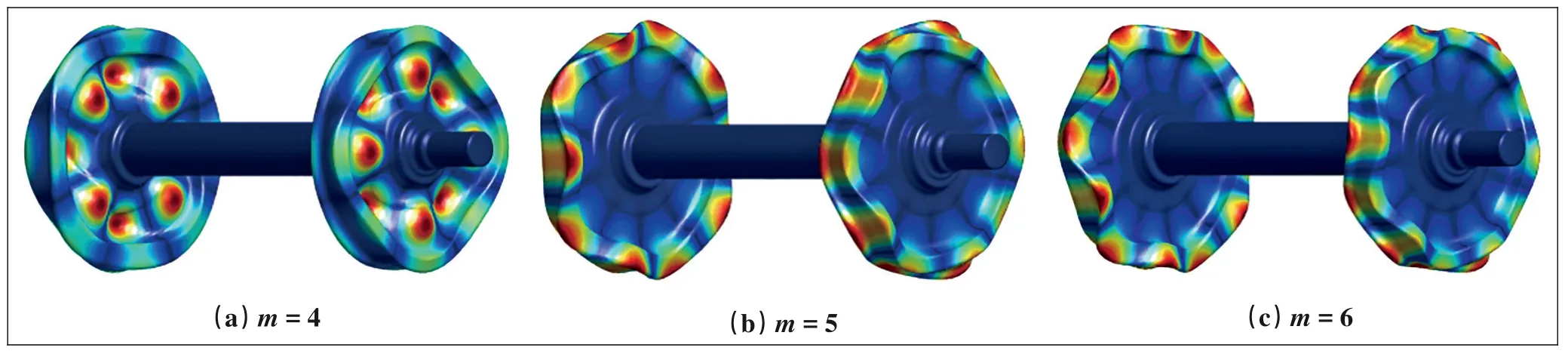
图6 轮对模态

2.2 简谐轮轨力作用下轮对声辐射

2.1节描述了如何计算旋转轮对在简谐轮轨力作用下的振动。轮对表面振动可以确定其声辐射, 即振动的轮对向周围空气辐射的声功率或给定测点的声压。以前考虑轮对声辐射时, 没考虑轮对的旋转和移动, 即把轮对当成只是振动的静止物体。在此前提下, 经典的亥姆霍兹-克希霍夫（Helmholtz-Kirchhoff）声学积分方程成立, 并通常用声学边界元方法求解[5］。当车速不高时, 允许这样做, 但对于高速轮对, 这样做会产生很大误差, 尤其对于声的频谱, 其完全忽略了移动声源的多普勒效应。

随着高速铁路建设, 轮对声源的移动效应越来越受到重视。文献[3-4, 6］研究表明, 轴对称旋转轮对在简谐轮轨力作用下的振动如果通过固定在车体上的激光测振仪测量（在力学里, 被称为在欧拉坐标系下描述轮对的振动）, 则测量到的振动依然是简谐振动, 且振动频率与作用力频率相同。因此, 如果不考虑空气与轮对表面间的黏滞性, 则包裹在轮对周围的空气也将做同频率的简谐振动。但由于轮对移动会产生多普勒效应, 因此经典的亥姆霍兹-克希霍夫声学积分方程不再适用。为此, 文献[7］在忽略气动效应的前提下, 通过推导出移动单极子和偶极子声源的声辐射表达式, 建立计算移动同时又做简谐振动物体的声学边界积分方程。由于问题的复杂性, 文献[7］只针对轴对称物体沿对称轴方向移动这一特殊情形编写边界元程序（边界元网格为二维）。文献[7］算例表明, 振动物体高速移动对声场有很大影响。虽然列车轮对大多数为轴对称, 但其移动方向不沿对称轴方向, 因此文献[7］编写的边界元程序无法应用。为此, 文献[8］在建立的轮轨噪声预测模型中采用近似方法求解移动轮对的声辐射, 即先不考虑轮对移动, 只考虑其振动, 应用声学边界元方法计算出声功率, 然后用相同声功率的简单声源代替轮对, 这些简单声源移动, 产生具有多普勒效应的声场。某高速铁路车轮（车轴固定但车轮可以旋转）在单位垂向轮轨力作用下辐射的声功率级见图7, 其中旋转对应车速350 km/h。可以看出, 旋转带来的频率分叉表现在辐射的声功率级上。

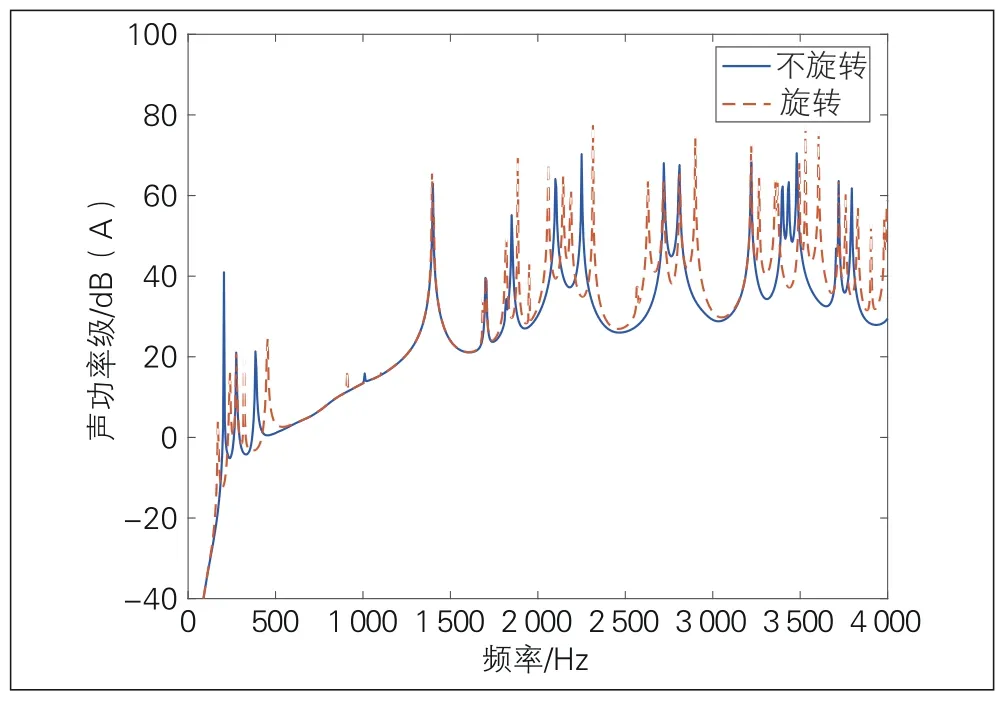
图7 某高速铁路车轮在单位垂向轮轨力作用下辐射的声功率级

在处理移动声源的声辐射时, 也有研究人员用“声源不动-观测点向反方向移动”模拟“声源移动-观测点不动”的真实情形。1个频率为500 Hz、体积速度为1 m3/s、移动速度为350 km/h的点声源在观测点（t=0时声源与观测点相距7.5 m）处产生声压级见图8, 其中蓝线为真实情况, 红线为“声源不动-观测点往反方向移动”的结果。可以看出, 差别明显。真实情况是, 声源趋近和离开过程中观测点声压级的时间历程不同。

图8 1个频率为500 Hz、体积速度为1 m3/s、移动速度为350 km/h的点声源在观测点处产生声压级

严格说, 移动且振动的物体声辐射问题是气动声学问题, 应该用气动声学理论, 如Ffowcs Williams and Hawkings（FW-H）方程[9］求解。由于气动声学分析复杂, 只能对很简单的情况分析[10-12］。目前在分析高速移动轮对的气动噪声时不考虑轮对振动[13］（即轮对只是移动的刚体）, 而在分析振动声辐射时, 不考虑移动带来的气动效应。总之, 同时旋转、移动、振动的轮对声辐射是还需要深入研究的问题。

3 轨道结构声振特性

高速铁路施工质量高、曲线半径大、扣件刚度低、轨道板与底座板间的联接刚度大, 因此, 从轮轨噪声研究角度, 高速铁路轨道结构可简化为由钢轨、扣件和轨道板组成的无限长周期结构, 周期等于1块轨道板的长度（记为L）, 轨道垂向振动模型示意见图9。所谓轨道结构声振特性, 指在静止不动或以速度c移动的单位简谐轮轨力作用下（假定每根钢轨同时受到1个单位垂向轮轨力）, 钢轨的频率响应、受力点两边钢轨振动的衰减规律（振动衰减率）以及钢轨和轨道板辐射的声压谱。单位简谐轮轨力在数学上表示为eiΩt, 此处i是虚数单位,Ω是角频率。

图9 轨道垂向振动模型示意图

3.1 轨道结构模态特性

钢轨在力作用点的垂向位移频率响应见图10, 当上述简谐力不沿钢轨移动（即c=0）时, 整个轨道结构均同频率简谐振动, 因此可画出力的作用点位移幅值与频率间关系曲线, 如图10中实线所示[14］。图中有2个峰值, 1个大约为126 Hz, 1个大约为940 Hz, 这2个峰值对应轨道结构的模态特征。第1个峰值产生是由于激发了钢轨的一个模态：在此模态下, 钢轨作为刚体在扣件刚度上发生共振, 因此频率可以通过下式估算：

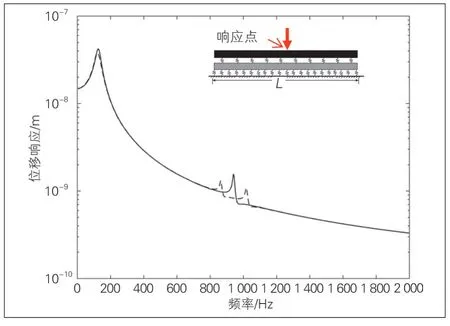
图10 钢轨在力作用点的垂向位移频率响应

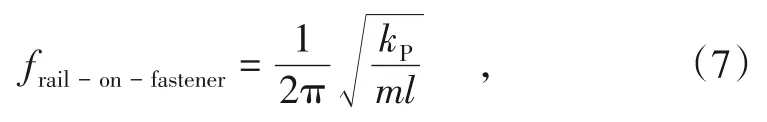
式中：kp为扣件刚度；m为单位长度钢轨质量；l为相邻扣件间距离。式（7）假定扣件垂向刚度为常数。目前高速铁路常用的扣件系统, 如WJ-7、WJ-8和Vossloh300等, 由于存在铁垫板, 其提供给钢轨的动刚度是频率的函数[15］, 即式（7）中kp与频率有关。另外一个峰值对应钢轨在扣件上的pinned-pinned振动, 这时, 扣件对钢轨来说如同铰支座, 在扣件位置, 钢轨振动最小；在跨中位置, 钢轨振动最大。这时, 任何1跨钢轨如同简支梁振动, 相邻跨的振动相位刚好相反, 钢轨只是振动, 不发生波动（或者说波动速度为无穷）。因此, pinned-pinned频率是1跨钢轨模型的第1阶固有频率[14］（见图11）。从图11可以看出, pinned-pinned频率主要取决于钢轨和跨距, 与扣件刚度关系不大。

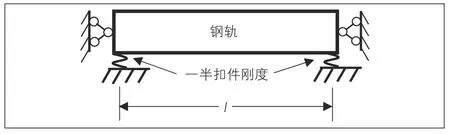
图11 计算pinned-pinned频率的力学模型

当上述简谐力是移动简谐力（即c≠0）时, 钢轨的任何一点振动不再是简谐振动, 而是瞬态的（由于扣件对钢轨的离散支撑造成）。但是, 如果观测点随作用力一起移动且保持与作用力的距离不变, 则观测到的响应可以表达为周期函数与上述简谐力的乘积, 即w(t)=Q(t,Ω)eiΩt, 其中Q(t,Ω)是时间t的周期函数, 周期等于简谐力通过1个轨道结构周期L的时间, 即L/c。当然Q(t,Ω)也是简谐力频率Ω的函数。由于Q(t,Ω)是时间t的周期函数, 其可以表达为傅里叶级数：

式（9）表明, 观测到的位移可以表达为一系列简谐振动的叠加, 其中第n个简谐振动的频率是即等于激励力频率加荷载过结构周期频率的n倍。

Q(t,Ω)也可以称为钢轨对移动简谐力的频响函数, 其不只依赖激励频率, 还与时间有关。可以给定t, 得出Q(t,Ω)与激励力频率间的关系曲线。给定不同时刻, 荷载将处于钢轨不同位置, 则Q(t,Ω)与频率间的关系曲线不同。图10中虚线为t=0时Q(t,Ω)与激励频率间的关系曲线, 此时, 作用力刚好处于轨道板跨中（也刚好处于2个扣件间）。作用力的移动速度为100 m/s。可以看出, 相比于作用力不移动的情形, 荷载移动使pinned-pinned峰分叉为2个, 1个大约为860 Hz, 1个大约为1 020 Hz, 且高度都比原有峰的高度低。另外, 荷载移动也使第1个峰值的频率和高度都降低。但在其他频率, 荷载移动并没有产生明显影响。总之, 荷载移动会改变轨道结构模态响应。

3.2 钢轨振动衰减率

3.1节中提到轨道结构的2个振动模态, 在整个轨道结构长度范围内, 钢轨振动不衰减。但在上述简谐力作用下, 由于实际轨道结构存在阻尼, 钢轨振动将随力距离的增加而衰减。如果荷载不移动, 则钢轨每一点都作简谐振动, 因此可以比较各处的振幅。假定纵向坐标为x的钢轨振幅为͂(x,Ω), 那么20log[͂(x1,Ω)/͂(x2,Ω)|]定义为位置x2相对位置x1的振动衰减量, 单位是dB。在离激振力比较远的地方, 钢轨振幅沿纵向位置变化规律可以近似为指数衰减函数, 即͂(x,Ω)=̂(Ω)e-αx, 其中α（一个正实数）为衰减系数, 单位是m-1。这时可定义相距为1 m的衰减量（称为衰减率）, 即：

钢轨振动衰减率是影响钢轨声辐射的重要因素。有研究表明[16］, 在其他条件不变的情况下, 衰减率每提高1倍, 钢轨辐射声功率可降低3dB。因此, 钢轨振动衰减率已成为轨道结构的重要声振特性指标。国际标 准EN 15461《Railway applications-Noise emission-Characterisation of the dynamic properties of track sections for pass by noise measurements》中描述了钢轨振动衰减率的测试和计算方法：钢轨振动衰减率测点见图12, 加速度计固定在钢轨上, 力锤敲击图12所示位置, 通过加速度计1和垂向锤击力产生垂向振动频率响应函数, 通过加速度计2和横向锤击力产生横向振动的频率响应函数。

图12中, c为加速度传感器所在位置, d为扣件区间标号, 黑色箭头a为力锤敲击位置在扣件正上方, 白色箭头b为力锤敲击位置在跨中。敲击点共29个。衰减率以1/3倍频谱形式给出, 其计算公式为：[16］

式中：DR为钢轨1/3倍频程振动衰减率, dB/m；A(x1)为加速度计位置处的原点频率响应函数在该1/3倍频程的有效值；A(xn)为第n个锤击位置与加速度计位置间的跨点频率响应函数在该1/3倍频程的有效值；Δxn为第n-1个锤击点与第n+1个锤击点间距离的一半（当n=1时Δxn取第2个锤击点与第1个锤击点间的距离）。文献[17-19］对实际轨道的振动衰减率进行测试研究。按图12的测试方法, 只能得到非移动荷载作用下的钢轨振动衰减率。

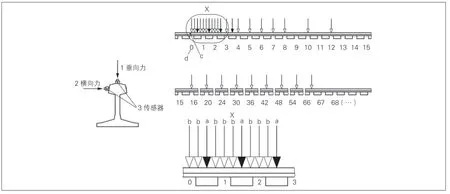
图12 钢轨振动衰减率测点

通过计算钢轨在静止或移动简谐力作用下的响应也可以计算出衰减率, 预测得到钢轨垂向振动衰减率见图13[14］, 其中实线为非移动荷载产生的衰减率, 是荷载不移动时的结果；虚线为移动荷载产生的荷载前方衰减率, 点画线为移动荷载后方衰减率, 在计算图13时, 假定了一个不随频率变化的扣件刚度。图13表明, 当频率小于钢轨在扣件刚度上的共振频率时, 钢轨中不产生波动, 因此衰减率较高, 达到8 dB/m, 在此频率范围内, 轨道板声辐射比钢轨声辐射高。当频率高于上述共振频率时, 钢轨振动衰减率急剧下降, 在pinned-pinned频率处达到最小值, 在此频率范围内钢轨声辐射比轨道板声辐射强很多。在频率约为500~2 000 Hz时, 由于轮对没有高声辐射模态（见图5、图7）, 钢轨振动衰减率很低, 因此钢轨对轮轨噪声的影响高于轮对的影响。

图13 预测得到钢轨垂向振动衰减率

图13中虚线和点画线是荷载高速移动时的结果。当荷载高速移动时, 荷载前、后方钢轨振动波不同, 因而导致荷载前、后振动衰减率不同（荷载不移动时, 荷载两边的衰减率相同）。通常, 荷载移动使钢轨低频范围内的振动衰减率大大降低（见图13中虚线和点画线）, 原因是荷载高速移动会激发轨道结构中的自由波。从图10可以看出, 荷载移动对荷载作用点处的位移影响不大, 但由于振动衰减率降低, 即在荷载前后相当长范围内钢轨振动比荷载不移动时增加很多, 这会增强轮对间通过钢轨发生的相互作用。

过去针对普速铁路研究轮轨噪声时只考虑1个轮对与轨道的相互作用, 忽略了相邻轮对间通过钢轨的相互作用。从上面移动荷载钢轨振动衰减率结果可知, 对高速铁路, 需考虑相邻轮对间通过钢轨的相互作用。

3.3 轨道结构声辐射特性

轨道结构声辐射包括2根钢轨的声辐射和轨道板声辐射。分别计算：计算钢轨声辐射时假定轨道板不振动, 只起声反射作用（轨道板没有任何吸声材料）或者声吸声作用（轨道板铺设吸声材料）, 在计算轨道板声辐射时, 假定钢轨不存在。钢轨与轨道板间有间隙, 该间隙在轨道方向不连续, 被扣件等距离隔断, 目前在计算钢轨声辐射时, 忽略扣件的隔断作用, 认为钢轨与轨道板间的间隙在纵向连续。即钢轨表面和轨道板表面形成的声学空间在轨道方向均匀。

轨道板声辐射计算相对容易。从声辐射角度看, 轨道板为置于无限大障板中的一个无限长有限宽的喇叭纸盆, 向障板一侧的半空间中辐射声音。如果认为轨道板振动在轨道板宽度方向均匀分布, 则所有轨道板振动合在一起可以从数学上表达为一系列不同振动频率、以不同波数沿轨道方向传播的振动波叠加（文献[14］对此做了详细推导）。事先把一系列不同振动频率f和不同波数β的、振动幅值为单位值的振动波的声辐射计算出来, 这些幅值为单位值的振动波声辐射可以通过波数域的瑞利积分公式计算[14］。根据声学理论, 只有当轨道板振动波波长（2π/β）大于声波波长（c0/f, 此处c0是声速）时, 轨道板才能辐射远场声。即对给定频率f, 只须考虑范围内的波数。对轨道板声辐射, 考虑频率在500 Hz以下, 所以需考虑的波速范围为|β|≤10 rad/m（取c0=343 m/s）。

钢轨振动声辐射计算较复杂。对频率为f, 纵向波数为β的钢轨表面法向振动速度可以表达为(s)ei2πfte-iβx, 其中͂(s)是x=0横截面边界的法向振动速度幅值, 这里s是沿该横截面边界度量的弧长。通过对钢轨做平面应变状态下的模态分析, 得到一系列以横截面边界法向位移表达的振型͂m(s), 那么͂(s)可表达为这些振型的线性叠加, 即：

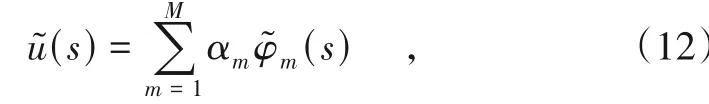
钢轨与轨道板间的间隙在轨道方向不连续, 被扣件等距离隔断。即钢轨、轨道板和扣件隔成了左右两边是开放的声腔。该腔对钢轨声辐射的影响, 目前还未进行充分研究。

4 轮轨高速高频相互作用和轮轨噪声估算

4.1 轮轨力

如果轮轨绝对平顺, 则轮轨间只有由于周期性过枕产生的动态轮轨力, 包含的频率成分只有过枕频率及其倍频。这种动态轮轨力在文献中被称为参数激励产生的轮轨力。应避免过枕频率接近钢轨在扣件刚度上的共振频率, 否则钢轨会发生强烈振动。由图10可知, 钢轨在扣件刚度上的共振频率是126 Hz, 因此, 对0.65 m的枕距, 当速度为295 km/h时, 过枕频率等于钢轨在扣件刚度上的共振频率。

当轮轨存在粗糙度时, 轮轨间产生额外的、通常比参数激励产生的轮轨力大很多的动态轮轨力, 其中包含丰富的频率成分。过去针对普速铁路轮轨噪声计算轮轨力时, 采用移动粗糙度模型[2］, 即假定轮对不动, 让1条粗糙度带在轮轨间往反方向移动。此方法使轮轨力计算简化, 但忽略了移动荷载效应, 不完全适合高速铁路。上述旋转轮对和无限长周期轨道结构动态特性为：

（1）旋转轮对在简谐轮轨力作用下轮轨接触点响应是简谐力且频率与作用力频率相同（见2.1节）。

（2）无限长周期轨道结构在移动简谐力作用下, 如果观测点随作用力一起移动且保持与作用力的距离不变, 则观测到的响应可以表达为周期函数与简谐力的乘积, 其中周期函数的周期等于简谐力通过一个轨道结构周期（L）的时间（见3.1节）。基于上述动态特性, 再假定轮轨粗糙度是纵向位置坐标x的周期函数, 周期等于轨道结构周期的整数（N）倍（即粗糙度的周期等于NL）。

（3）对轮轨赫兹接触方程进行线性化并假设轮轨始终保持接触, 即可应用文献[20］建立的傅里叶级数法计算轮轨力。在上述假设下, 轮轨力只包含以f0=为基频的谐波成分。这些谐波成分可以通过线性代数方程求得, 而且便于考虑多轮对与轨道结构的相互作用。即可通过此办法求出轮轨力的离散谱, 谱分辨率为, 因此只要选择足够大的N, 即可得到足够高的频率分辨率。例如, 对c=350 km/h,L=6.5 m的情况, 选择N=15（粗糙度周期为97.5 m）, 轮轨力频率分辨率为1 Hz。

因为1个轨道板布置的扣件数量一定, 且扣件间等距离, 因此轨道板长度（忽略轨道板与轨道板间的间隙）一定是扣件间的距离（或枕距）的整数倍。因此, 轮轨力中会有明显的过枕频率分量及其谐波。如果钢轨存在单一波长波磨或车轮存在单一阶次多边形, 相应的激励频率为fE, 而过枕频率为fS时, 则轮轨力谱在fE±nfS（此处n是一个正整数）频率范围出现峰值, 甚至导致车内噪声也出现此特征, 某高速铁路车内噪声声压级谱见图14, 其中586 Hz为粗糙度激励频率, 而过枕频率为128 Hz, 即调频现象, 是粗糙度激励和过枕参数激励相互影响的结果。因此, 基于振动或噪声信号判断轮轨粗糙度状态时, 须考虑上述调频现象。

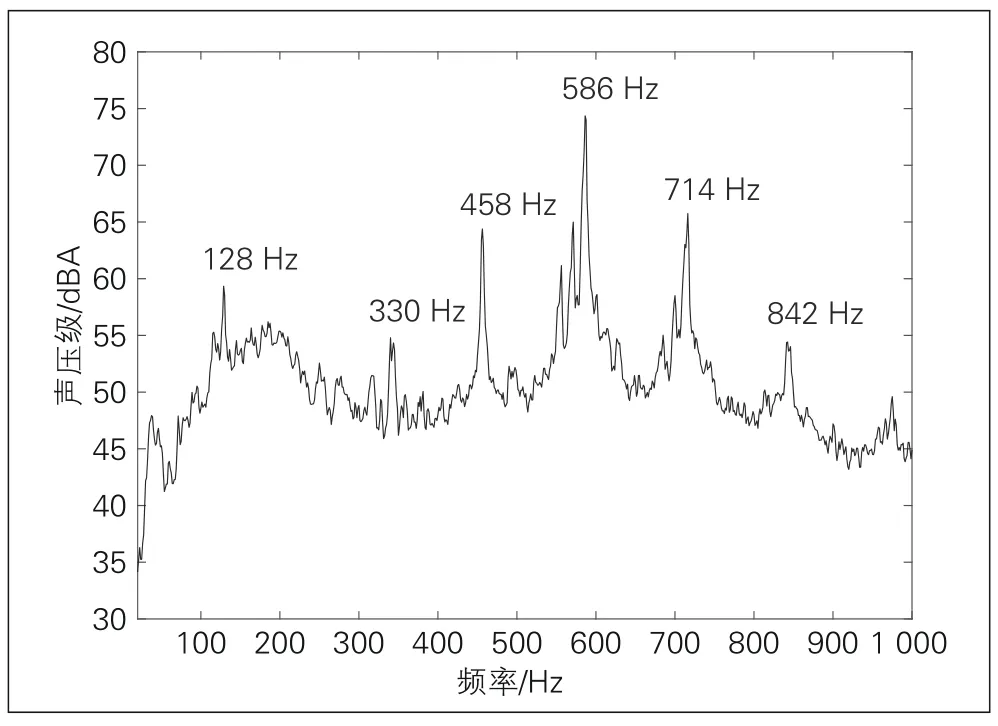
图14 某高速铁路车内噪声声压级谱

4.2 轮轨噪声

根据上述单位简谐轮轨力作用下轮对声辐射和轨道结构声辐射计算、在轮轨粗糙度激励下的轮轨力计算, 可通过相乘和相加的过程计算轮轨噪声。在评价列车通过噪声时, 给出的量化指标是列车通过过程中测点A计权等效声压级。因此预测轮轨噪声时, 应确定整个列车编组所有轮对通过过程中产生的声辐射。8编组列车有32个轮对, 同时考虑32个轮对与轨道结构的相互作用在计算上目前存在困难, 因此需作简化（见图15）。

图15 轮轨噪声计算简化

考虑同一车辆的2个转向架间距离相对较远, 可分2次计算轮轨噪声。第1次计算时, 假定只有第1个转向架的2个轮对, 计算出轮轨力及轮对和轨道结构产生的声压谱。对该声压谱相位作相应延后, 作为最后2个轮对单独存在时产生的声压谱；第2次计算时, 假定只有第2和第3个转向架的4个轮对, 计算出4个轮轨力及轮对与轨道结构产生的声压谱。对该声压谱相位作相应延迟, 作为其他相邻转向架4个轮对单独存在时产生的声压谱。可进一步区分4个轮对全是拖车轮对、全是动车轮对、部分拖车部分动车轮对等不同情况。整列车通过时产生的轮轨噪声按式（13）计算：

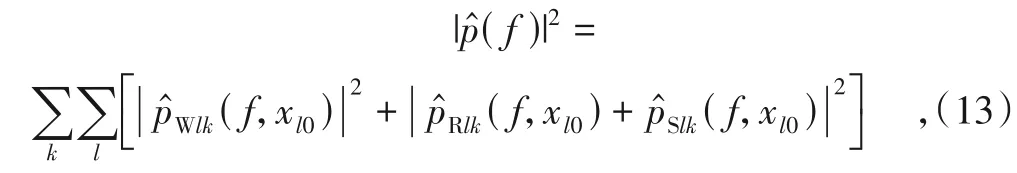
式中：̂(f)为列车通过时观测点产生的频率为f的声压谱, Pa/Hz；̂Wlk(f,xl0)为第l个轮对由于第l个轮轨力中的第k个频率分量产生的声压谱；̂Rlk(f,xl0)为钢轨由于第l个轮轨力中的第k个频率分量产生的声压谱；Slk(f,xl0)为轨道板在第l个轮轨力中的第k个频率分量激励下产生的声压谱；xl0为t=0时刻第l个轮对的位置。式（13）表明, 在计算列车通过产生的轮轨噪声时, 假定各轮对辐射的声压谱之间和轨道结构辐射的声压谱之间相互独立, 因此通过非相干相加（即能量相加）得到总声压谱, 钢轨辐射的声压谱和轨道板辐射的声压谱之间相干, 因此采取代数相加。另外, 假定轮轨力中各频率分量间也不相干。有了各部分辐射的声压谱, 即可通过傅里叶逆变换得到各部分产生的声压时间历程。这些声压时间历程相加得到列车通过过程中产生的轮轨噪声声压时间历程。

对高架桥梁线路的某高速列车在测点（横向离轨道中心线25 m, 垂向离轨顶3.5 m）的A计权连续等效声压级进行轮轨噪声预测, 并与实测列车通过噪声对比（见图16[21］）。由图16可知, 预测轮轨噪声总值比通过噪声总值小2 dB（A）左右, 且实测总值与列车速度间关系可近似为SPL=27 log10(V/160)+b（即实测噪声随速度对数增加率为27, 而预测轮轨噪声增加率为26）, 对于该测点, 轮轨噪声主要是列车通过噪声。由图16（b）可知, 800 Hz以上频段, 预测轮轨噪声谱与实测通过噪声谱接近, 可知轮轨噪声频段是800 Hz以上的高频段；500 Hz以下频段, 通过噪声主要是气动噪声和桥梁结构噪声。

5 轮轨噪声控制措施

经过几十年的理论研究和工程实践, 轮轨噪声的控制措施可分为源头控制措施和路径控制措施。路径控制措施主要是声屏障[22］, 其效果很好, 但建设和维护成本很高；源头控制措施包括轮轨粗糙度控制、车轮控制和轨道控制。

5.1 轮轨粗糙度控制

由以上分析可知, 轮轨粗糙度是轮轨噪声产生的根源。对速度在250~400 km/h的高速列车, 需考虑的钢轨粗糙度波长为0.02~2.22 m, 车轮多边形的阶次范围为1~130。如何通过旋修和打磨控制轮轨粗糙度, 使轮轨噪声低于某个限值是需要研究的课题。需建立基于轮轨噪声限值的轮轨粗糙度标准, 以指导轮轨表面状态维护。

5.2 车轮控制

车轮控制的基本出发点是增加车轮阻尼。轮对在自由状态下的阻尼很小, 模态耗散因子为万分之几的数量级。轮对通过轴箱与一系悬挂连结后, 可以从一系减振器获得一定的阻尼, 但主要是增加轮对弯曲模态（节径数等于1）的阻尼, 对节径数≥2模态（这时车轴基本不动）的阻尼, 则影响不大。车轮声辐射主要靠节径数≥2的模态（图5中频率高于约2 000 Hz的模态）。轮对在自由状态下, 这些模态的阻尼很低, 因此采取车轮控制, 在自由轮对试验时, 效果十分明显。当轮对在钢轨上滚动时, 轨道结构对轮对不但是相互作用的对象, 同时也给车轮增加了约束和振动能量耗散路径（轮对与轨道接触后, 轮对振动能量通过轨道结构耗散一部分）。因此得出轮对从轨道结构获得了比自身大很多阻尼的结论。如果车轮控制给车轮增加的阻尼远没有轨道结构给车轮的阻尼大, 则这些控制措施在轮对沿钢轨滚动时不会有效果。轮对和轨道结构的振动由轮轨力产生, 轮轨力相对轮轨系统是内力, 只会使轮轨系统总能量减少, 不会增加。轮对和轨道结构耗散能量（包括轮对耗散能量、轨道结构耗散能量以及接触斑内耗散能量）来自列车牵引系统。

研究表明, 对普通轮轨系统, 在约2 000 Hz以上的频率范围内, 轮轨噪声主要来源是轮对。高速铁路轮轨噪声主要来源也是轮对[21］, 高速铁路轮轨噪声主要控制措施：

（1）车轮形状优化。刘林芽等[23］研究车轮形状的影响, 结果表明车轮直径增大、辐板径向尺寸增大、轮辋旋修深度增大、辐板厚度减小都会使车轮噪声增大。

（2）约束阻尼层。在车轮腹板上粘贴约束阻尼层, 增加车轮阻尼。意大利Syope约束阻尼层车轮的示意及实物见图17, 安装在ETR500高速列车上, 文献[24］指出, 列车运行速度为200~300 km/h时, 约束阻尼层可降低轮轨噪声4~5 dB（A）。约束阻尼层缺点是容易脱落。

图17 意大利Syope约束阻尼层车轮

（3）TMD（Tuned mass damper）。车轮不同形式的动力吸振器[25］（见图18）基于动力减振器原理设计：把原始车轮作为主结构, 通过动力吸振器抑制主结构特定频率的振动。

图18 车轮不同形式的动力吸振器

（4）阻尼环。在车轮轮箍内侧预先开设凹槽内嵌入钢环形成阻尼环车轮（见图19）。列车运行时, 车轮与钢环通过摩擦耗能。阻尼环预紧力对阻尼环耗能效果影响很大：预紧力太小则摩擦力太小, 达不到摩擦耗能的目的；预紧力过大, 阻尼环与车轮间没有相对运动, 也达不到摩擦耗能的目的。在半消音室通过摆锤锤击试验测定阻尼环对车轮辐射声功率的影响（见图20）。可以看出, 阻尼环（尤其是双环）可以有效降低1 500 Hz以上的声辐射[26］。

图19 阻尼环车轮

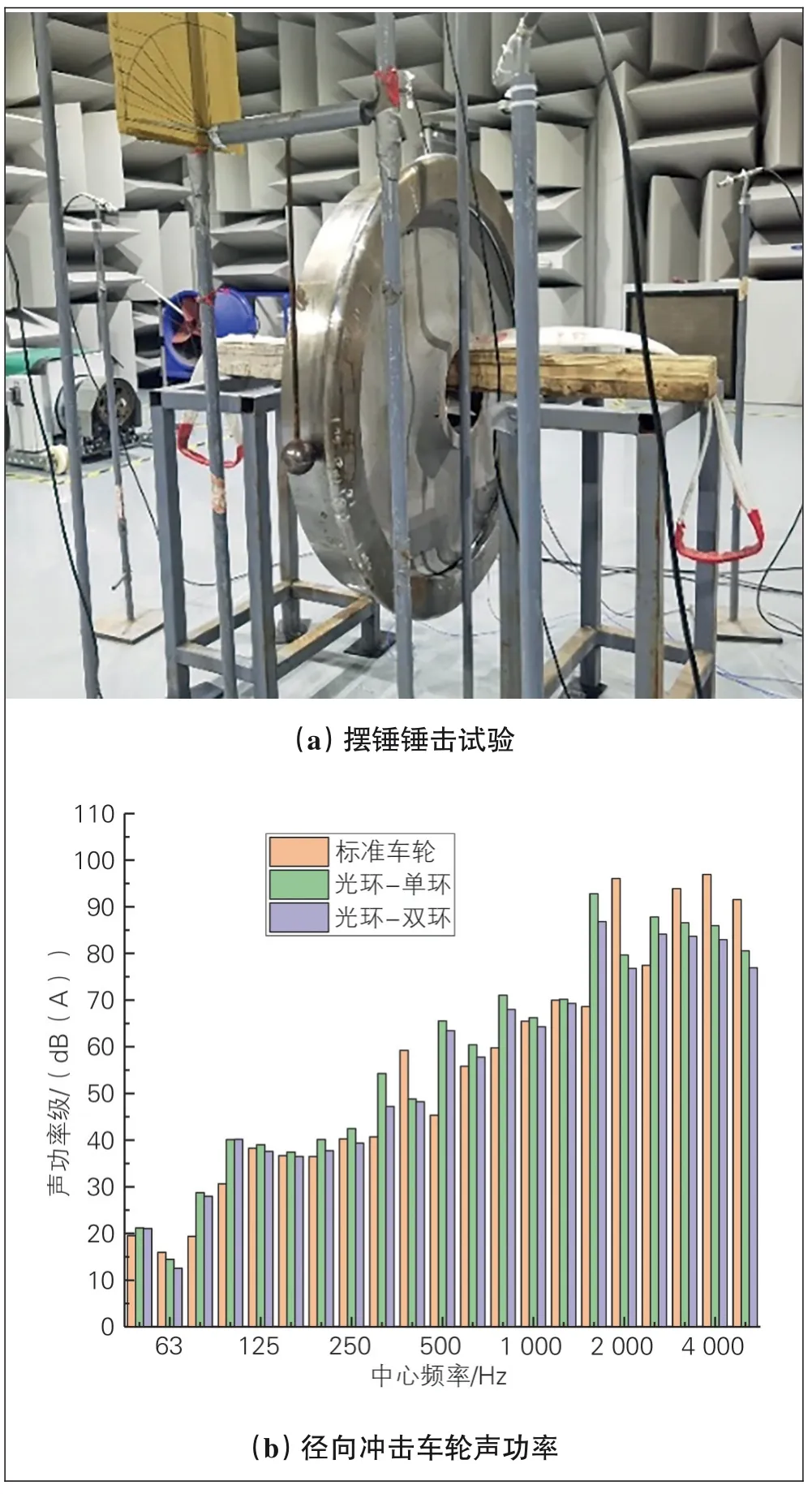
图20 阻尼环对车轮声辐射的影响

目前设计车轮降噪措施时, 没考虑轮对的高速旋转, 此类降噪措施可能达不到理想效果（旋转使频率发生分叉, 偏离降噪措施设计时的频率）。现有研究假定轮对是轴对称体, 许多降噪措施把轮对从轴对称体变为环向周期结构（见图18）。葛帅等[27］以高铁所用TMD车轮为例, 计算了车轮在2个不同轮轨接触点（1个位于2个TMD之间, 1个位于TMD的正下方）处的径向频率响应函数, 结果表明, 上述2个位置的频响函数差别很大, 在特定频率可以相差60 dB以上。文献[27］的预测并没有考虑车轮旋转, 但结果表明, TMD车轮不能看成是轴对称体（轴对称车轮滚动圆上各个点的动力学完全相同）。截至目前, 尚不清楚环向周期性、车轮高速旋转和移动等因素对轮对声辐射特性的影响规律。

5.3 轨道控制

对于高速无砟板式轨道结构, 需保护轨道板, 扣件刚度比传统有砟轨道低很多。因此, 高速无砟板式轨道结构的声辐射主要由钢轨主导。因此, 轨道控制应有利于控制钢轨声辐射。

（1）提高钢轨振动衰减率。提高扣件刚度, 使更多振动能量传递到轨道板, 以提高钢轨振动衰减率, 但同时也会增加轨道板声辐射（可以在轨道板上铺设吸音材料以控制轨道板声辐射）。提高扣件阻尼也会提高钢轨的振动衰减率。我国高速铁路常用扣件有WJ-7、WJ-8、Vossloh300三款, 扣件包括高分子材料弹性垫板、铁垫板、弹条。铁垫板和弹条使扣件提供给钢轨的动刚度具有模态特征, 在扣件系统模态频率处, 动刚度很低。因此, 弹性垫板本身的动刚度不同于扣件系统的动刚度, 且差别随频率增加而增加。

（2）安装扣件间的钢轨动力吸振器[28］（见图21）。假定钢轨固定不动, 则钢轨动力吸振器可简化为质量-弹性（阻尼）系统, 其固有频率为钢轨动力吸振器的调谐频率。当钢轨振动时, 钢轨动力吸振器给钢轨提供动刚度, 在调谐频率处, 动刚度最大。最大的动刚度与钢轨动力吸振器刚度k成正比, 但与其阻尼损耗因子成反比。在给定调谐频率时, 增加钢轨动力吸振器质量有利于增加钢轨振动衰减率。钢轨动力吸振器提高钢轨振动衰减率的机理除上述的动刚度外, 还与周期结构的波动特性（通带、禁带）有关[28］。

图21 钢轨动力吸振器

6 结束语

阐述轮轨噪声对高速铁路通过噪声的重要性、轮轨噪声的发声机理及其力学模型、轮轨噪声的预测流程、轮轨噪声的特性规律和影响因素、以及尚需要深入研究的问题。高速轮轨噪声是轮轨高速高频相互作用的结果, 关键影响因素包括波长2 m以下的钢轨粗糙度、阶次130以下的车轮不圆度、节径数≥2的轮对模态以及钢轨振动衰减率。针对典型高速铁路测试和预测表明：轮轨噪声在远场测点处的声压级与车速的对数可近似为线性关系, 比例系数约为27；在350 km/h甚至更高速情况下, 列车通过噪声主要是轮轨噪声, 且轮轨噪声频段主要在800 Hz以上；轨道板、钢轨和轮对分别在低频段（尤其是低于钢轨在扣件刚度上共振频率的频率）、中频段（尤其是钢轨pinned-pinned频率附近的频率）和高频段（高于轮对节径数≥2的最小模态频率）是轮轨噪声的主要贡献者；施加在轨道板、钢轨和轮对的降噪措施分别按对应频段进行设计；轮对降噪措施不但针对高频, 而且增加的阻尼应与轨道结构提供给轮对的阻尼相当或更高。

控制轮轨噪声, 需确定（所有的）轮对和（两条）钢轨哪个是主要噪声来源。轮轨噪声预测模型可以确定噪声来源, 但有效的现场试验方法还有待建立。旋转且移动轮对的振动声辐射还需深入研究。在设计轮对降噪措施时需考虑轮对旋转的影响；扣件弹性垫板的动刚度不能代表扣件系统的动刚度, 扣件系统的动刚度测定或预测还有待加强；钢轨动力吸振器在城市轨道交通得到广泛应用, 在高速铁路的可应用性也值得研究。