时速400 km高速道岔设计关键技术

王平, 徐井芒, 郝超江, 陈嵘, 姚力

（1.西南交通大学 高速铁路线路工程教育部重点实验室, 四川 成都 610031；2.西南交通大学 土木工程学院, 四川 成都 610031；3.中铁二院工程集团有限责任公司 土木建筑设计研究一院, 四川 成都 610031）

0 引言

针对我国“交通强国”战略发展目标, 开展时速400 km高速铁路设计、建造、运营、维护成套技术研究, 推动高速铁路技术实现新提升, 打造一条时速400 km高速铁路示范线, 是当下新的战略任务[1］。道岔是铁路线路中引导列车换线运行的关键设备, 也是轨道三大薄弱环节之一。高速列车过岔时, 由于轮轨接触点迹不连续, 将产生剧烈的轮轨动态相互作用[2］。随着列车运行速度的提升, 动力冲击相互作用显著加剧, 使轮轨系统产生剧烈的中、高频振动, 对保障道岔钢轨使用寿命和行车平稳性、安全性提出了挑战。

为了缓解道岔区域轮轨相互作用, 提高列车运行品质、减少道岔设备损坏, 应合理优化车轮与道岔之间的轮轨关系, 并开展道岔结构创新技术研究。在既有文献中, 德国BWG公司创新性地提出一种动态轨距优化技术（FAKOP）, 大幅降低了道岔横向结构不平顺, 以解决列车过岔晃车严重的问题[3］；在FAKOP技术基础上, 西班牙道岔专家Bugarin等[4］对直基本轨轨顶进行刨切, 进一步优化了道岔横向结构不平顺；王平等[5］提出通过优化直基本轨轨头廓形, 抵消轮对所受横向力；王树国等[6］通过抬高尖轨缩短轮载过渡范围, 有效减少了高速客运专线的道岔结构不平顺。

道岔由钢轨、扣件、轨枕、轨下基础等部件组成, 各部件间应满足等强度、等寿命、弹性连续等性能匹配要求。当运营条件变化时, 道岔各部件应根据运营需求进行结构创新或结构优化设计。目前, 我国已形成时速350 km高速铁路成套道岔结构, 随着时速400 km以上高速铁路的建设, 针对高速道岔开展适应性研究十分必要。

1 18号道岔对时速400 km高速列车的适应性研究

1.1 车辆-道岔耦合模型建立

以某高速列车车辆及18号高速道岔为原型, 建立车辆-道岔耦合模型（见图1）, 模型包含车辆模型、道岔模型、轮轨接触模型3个部分。

如图1（a）所示, 车辆模型由1个车体、2个转向架、4个轮对组成, 各包含6个自由度, 共计42个自由度。车辆模型主要参数参照文献[7］, 模型的一系悬挂、二系悬挂均采用弹簧阻尼元件模拟。

道岔为多根钢轨件组合而成的系统结构, 高速列车直向过岔, 车轮分别与直基本轨、曲基本轨、直尖轨接触, 在曲基本轨与直尖轨拼接位置发生轮载过渡。将曲基本轨、直尖轨组合的钢轨廓形作为一侧钢轨与车轮接触, 直基本轨与另一侧车轮接触。组合廓形一侧, 选取关键特征断面沿纵向插值获取任意位置的道岔组合截面廓形, 按里程等间隔布置, 基于Bezier曲线拟合生成连续的道岔变截面廓形。如图1（b）所示, 轨下基础模型的弹性用弹簧阻尼元件模拟。

通过轮轨接触模型, 将车辆模型与道岔模型连接, 轮轨接触的法向力与切向力分别使用Hertz非线性弹性接触和修正的FastSim进行计算[8-10］。

1.2 风险性评估

运用车辆-道岔耦合模型, 对运营时速400 km（检算时速440 km）高速列车直逆向通过18号道岔的动力学指标进行计算, 并与运营时速350 km（检算时速385 km）高速列车直向过岔的动力学指标进行对比（见图2）, 分析采用18号道岔的风险性。

如图2（a）所示, 运营时速400 km（检算时速440 km）高速列车直逆向过岔时, 其脱轨系数幅值相对于运营时速350 km（检算时速385 km）高速列车增长不大。

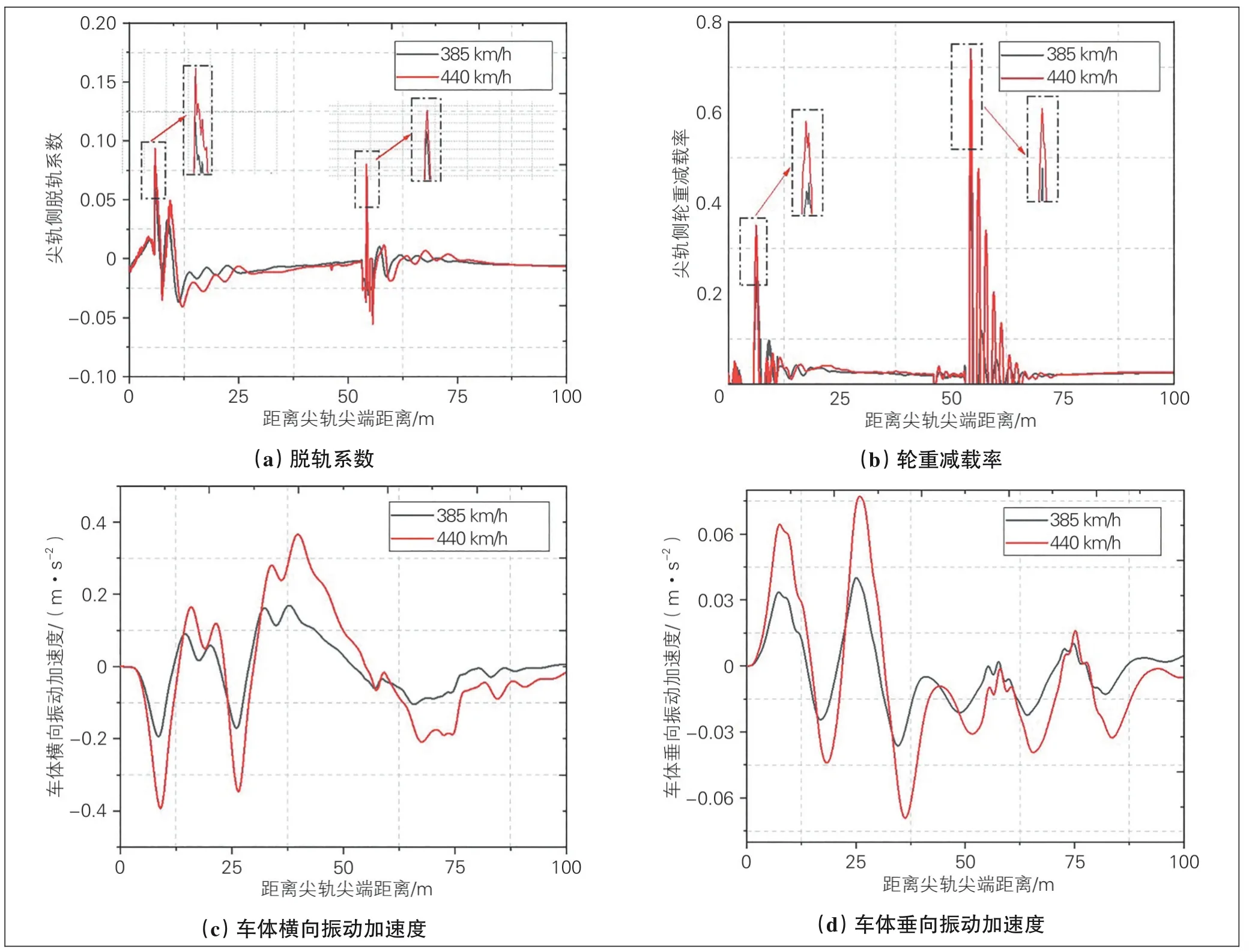
图2 高速列车通过18号道岔动力学指标时程曲线

如图2（b）所示, 轮重减载率最大值在辙叉区, 轮重减载率由0.543增至0.740, 速度增加对轮重减载率影响较大, 运营时速400 km（检算时速440 km）高速列车在辙叉区的轮重减载率接近限值0.8, 影响行车安全。

如图2（c）所示, 运营时速400 km（检算时速440 km）高速列车车体横向振动加速度最大值为0.39 m/s2, 运营时速350 km（检算时速385 km）高速列车车体横向振动加速度最大值为0.16 m/s2。

如图2（d）所示, 运营时速400 km（检算时速440 km）高速列车车体垂向振动加速度最大值为0.08 m/s2, 运营时速350 km（检算时速385 km）高速列车车体垂向振动加速度最大值为0.04 m/s2。

以上计算结果均未超过动力学指标安全限值, 但该车辆-道岔耦合模型未考虑环境等随机因素作用。在实际环境中, 如风荷载、轨道随机不平顺等因素不可避免。考虑各种随机因素与道岔结构不平顺叠加, 得到直基本轨与直尖轨的轨道谱（见图3）。如图所示, 将随机因素与道岔结构不平顺叠加后, 道岔区轨道谱相对于区间线路明显恶化。随着过岔速度的提升, 高速列车直逆向过岔时的车体横向加速度超限几率大幅增加, 即直向过岔“晃车”。一旦出现“晃车”现象, 查找原因、制定维修对策、现场整治等耗时较长, 影响联调联试；线路开通后, 道岔平顺性难以长期保持, 可能经常性出现“晃车”现象, 严重影响行车安全性、平稳性。

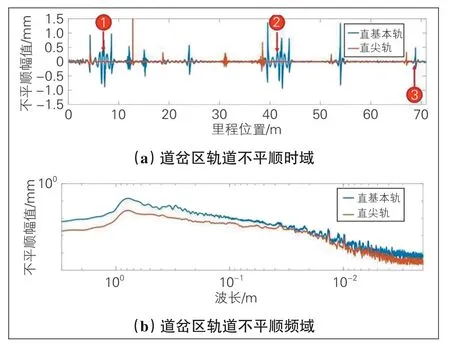
图3 道岔区轨道谱

2 轮轨关系优化

2.1 心轨降低值优化

在无缝线路中, 为了确保心轨在温度力作用下伸缩, 心轨尖端在辙叉咽喉后40 mm。现有18号道岔心轨尖端位置轨头宽度为9.2 mm, 心轨降低值为16 mm。为了改善轮轨动力冲击作用, 对心轨降低值进行优化, 将长心轨顶宽20.0 mm断面作为承载起始断面, 该断面心轨降低值为4 mm；顶宽50.0 mm时, 心轨完全承载, 心轨降低值为0 mm（见表1）。

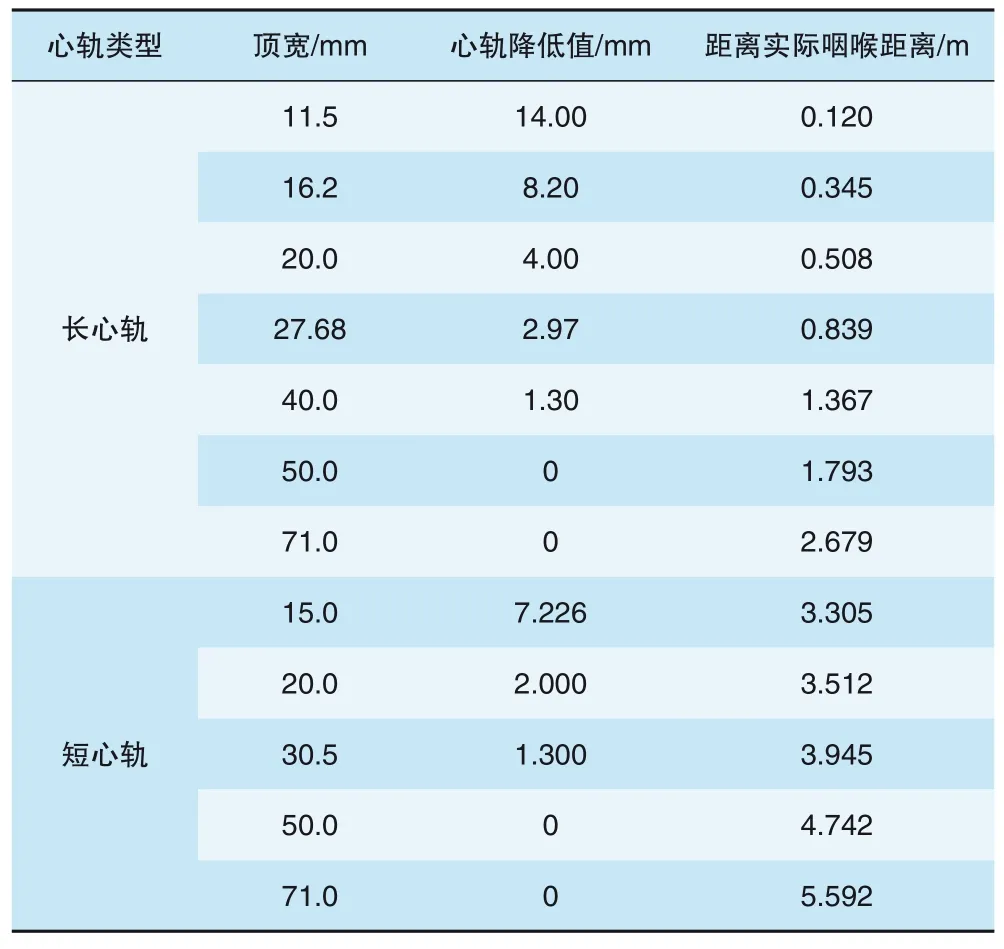
表1 辙叉心轨降低值设计

心轨降低值优化前后轮轨相互作用力时程曲线见图4。在优化轮轨关系与原始轮轨关系下, 轮轨横向力最大值分别为9.6 kN和10.7 kN, 轮轨关系优化后, 轮轨横向力小幅减小；在优化轮轨关系与原始轮轨关系下, 尖轨侧轮轨垂向力最大值分别为173.0 kN和183.3 kN, 轮轨关系优化后, 轮轨垂向力最大值减小。

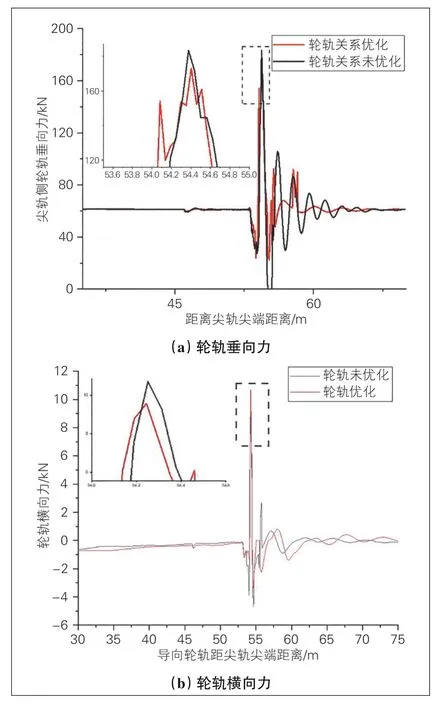
图4 心轨降低值优化前后轮轨相互作用力时程曲线

2.2 翼轨抬高

可动心轨辙叉在轮载过渡时, 由于垂向结构不平顺较大, 在辙叉区造成剧烈的轮轨冲击, 当列车以时速440 km直逆向过岔时, 轮重减载率接近限值。通过垂向抬高翼轨, 减小辙叉区垂向结构不平顺, 延后轮载过渡位置至心轨粗壮断面, 减缓辙叉轮轨动态相互作用。为了降低辙叉纵向不平顺, 将心轨20 mm断面作为承载起始断面, 翼轨抬高范围为心轨实际尖端至心轨50 mm断面；在心轨30 mm断面处, 翼轨抬高值达到最大, 为2.2 mm；在心轨20 mm断面处, 翼轨抬高值为0.7 mm。翼轨抬高前后系统动力响应对比见图5。如图所示, 通过翼轨抬高, 列车直逆向过岔的轮轨垂向力最大值减小14.60 kN。翼轨抬高使轮载过渡位置延后, 有利于减缓心轨薄弱断面伤损, 延长道岔心轨使用寿命。

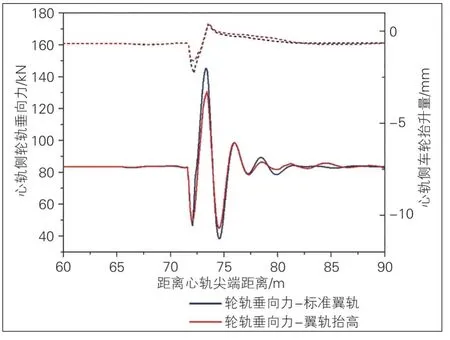
图5 翼轨抬高前后系统动力响应对比

2.3 低等效锥度基本轨结构优化

列车直逆向过岔时, 在转辙器区轮载过渡前, 由于曲基本轨向外弯折, 导致尖轨侧轮轨接触点外移, 使轮对滚动圆半径差增大, 加剧列车横向动力响应。为使列车平稳过岔, 提出通过切削直基本轨轨距角的方式控制滚动圆半径差, 从而对基本轨结构进行优化。通过优化直基本轨轨顶廓形, 使在转辙器区轮载过渡前两侧轮轨接触点同步外移, 减小了两侧滚动圆半径差和等效锥度。转辙器直基本轨优化方案示意见图6。

图6 转辙器直基本轨优化方案示意图

如图所示, 截面A-A位于尖轨尖端, 截面B-B位于直尖轨变截面范围末端, 即顶宽71 mm直尖轨所在位置。即使在轮对无横移量情况下, 变截面钢轨和曲基本轨弯折也会使轮对在截面A-A、截面B-B范围内产生滚动圆半径差。因此, 拟定截面A-A与截面B-B之间的尖轨变截面范围为直基本轨优化范围。当高速列车直逆向过岔且尖轨侧轮载开始从曲基本轨过渡至直尖轨时, 轮对滚动圆半径差和等效锥度较大。将轮载过渡起始位置相应的直基本轨截面C-C作为控制断面, 通过对截面A-A、C-C、B-B相应的直基本轨廓形离散点之间进行线性插值, 以模拟直基本轨廓形变化。采用结合Quasi-Newton和BFGS方法的二次序列优化法（SQP）, 对直基本轨C-C断面进行优化[5］。

基本轨优化前后系统动力响应对比见图7。如图所示, 该优化设计显著降低了轮载过渡时的轮轨横移量、车体横向振动加速度, 其最大值分别降低56.2%、50.0%, 行车平稳性显著提高。

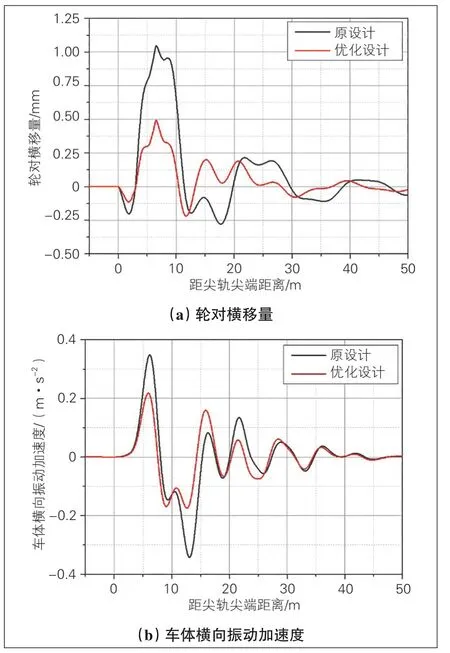
图7 基本轨优化前后系统动力响应对比

该方案对减小直向过岔横向力有一定帮助, 但增大了直基本轨一侧垂向力；侧向过岔时, 引起横向力增大, 给列车侧向过岔的安全性、平稳性造成一定隐患；工厂试制结果表明, 曲面轮廓的机加工难度非常大, 在运用实践中, 轮廓能否保持、打磨过程中能否恢复, 均需要进一步研究。

3 无缝化设计

3.1 转辙器跟端限位器优化

在莫喀高铁道岔结构设计中, 在尖轨跟端布置了2组跟端限位器。通过无缝道岔计算模型[11］, 分析纵向力传递机理以及由横向力引起的胀轨规律。在传统设计中, 转辙器跟端不同位置限位器子母块间隙均相等。若2组限位器子母块间隙相等, 通过计算可知, 靠近尖轨尖端的限位器所受集中纵向力, 远大于靠近尖轨根端的限位器[5］。不同位置的限位器由于受力不均, 易破坏道岔的几何形位状态, 在纵向力集中处可能导致钢轨碎弯。因此, 提出将2组限位器子母块间隙设置为不同值。根据计算将其差值调整为2 mm, 不同限位器子母块间隙组合下, 无缝道岔钢轨受力及尖轨尖端伸缩位移见图8。如图所示, 通过优化调整2组限位器子母块间隙, 纵向力差值显著减小, 最大限度满足了同步受力的要求。

图8 无缝道岔钢轨受力及尖轨尖端伸缩位移

3.2 新型锁闭结构

传统的尖轨外锁闭装置通过螺栓将尖轨连接铁与锁闭钩相连, 锁闭钩可在销轴内沿纵向在一定长度范围内平动；新型钩型锁闭机构在尖轨连接铁与锁闭钩之间有一个双层滑块, 锁闭钩可绕双层滑块转动, 以适应可动轨件伸缩。该新型锁闭结构可满足时速400 km高速道岔的钢轨高温差伸缩变形需求。2种锁闭装置结构对比见图9。

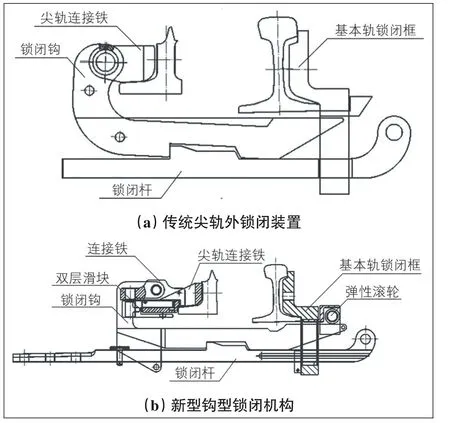
图9 2种锁闭装置结构对比

4 结论与建议

对时速400 km高速道岔设计关键技术的研究表明, 采用心轨降低值优化、翼轨抬高、低等效锥度基本轨结构优化等设计, 可在一定程度上改善轮轨动力冲击作用, 提升高速道岔的安全性与稳定性；通过优化尖轨跟端传力结构、采用新型钩型锁闭机构, 可进一步保障高速道岔无缝化, 满足跨区间无缝线路要求。研究已实现轮轨关系设计、跨区间无缝线路高平顺性等方面的高速道岔结构优化, 并对今后的研究方向提出以下建议：

（1）综合现有优化设计方案, 以高速行车低动力、高平稳性、高安全性等为目标, 利用多目标优化方法对轮轨关系进行优化。

（2）现有评估方法是基于车辆-道岔耦合动力学的方法, 所计算工况为理想状况下的单一工况, 后续在设计优化方案时, 宜将随机动力学、概率密度演化等方法引进, 以此评估动力学响应。