一类保持线性函数的算子的逼近

任美英

(武夷学院数学与计算机学院，福建 武夷山 354300)

1 引言

自Phillips[1]1997年构造研究q-Bermstein算子以来，有许多学者致力q-微积分在逼近论中的应用研究，如文献[2-10].近年，任[11]引进并研究了只保持常数的修正q-Durrmeyer型算子Mn，q(f；x)的逼近性质.本文的目的是引进算子Mn，q(f；x)的变种，使得新引进的算子能保持线性函数，并对该算子列的逼近性质加以研究.

本文涉及的q-整数和q-微积分的一些相关概念可见文献[12-13].设q＞0是任意固定的实数，k是非负整数，q-整数和q-阶乘定义如下:

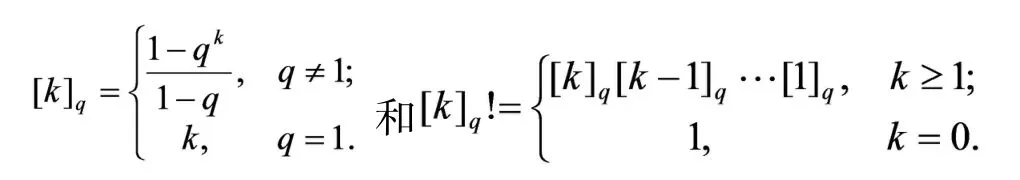
对非负整数n，k，n≥k，q-二项式系数定义为

让q＞0，对非负整数n，(a-b)n的q模拟定义为:.

q-Jackson积分定义为:

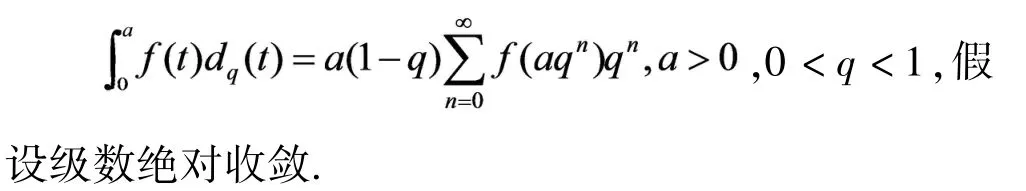
注:本文中，‖f‖表示｜f(x)｜在区间[0.1]上的最大值.C是一个常数，在不同处可能表示不同的值.

2 算子的构造

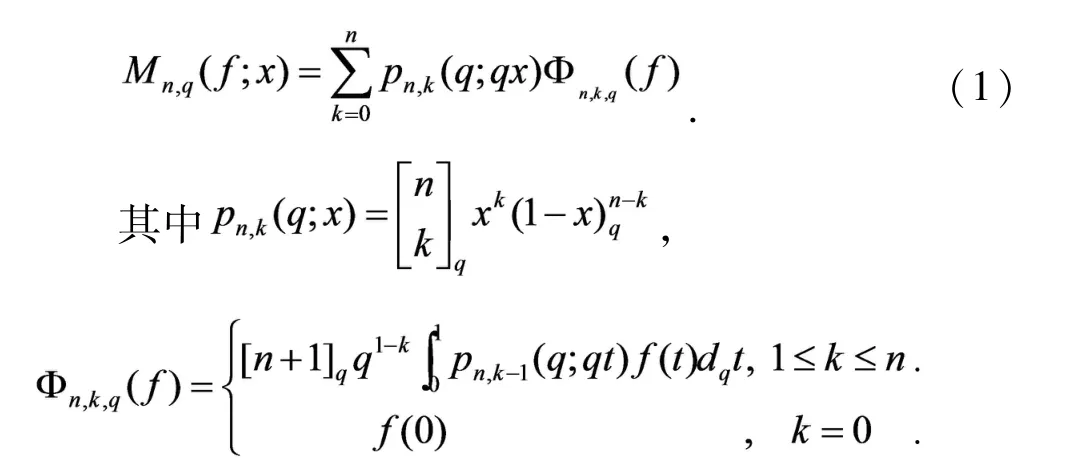
通过计算可得到算子Mn，q(f；x)的如下矩量.

引理1[11]对(1)式给出的算子Mn，q(f；x)，有

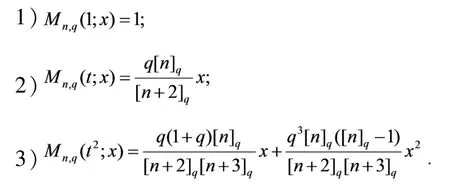
依引理1易得，Mn，q(f；x)只保持常数函数.为提高{Mn，q(f；x)}收敛速率，本文对Mn，q(f；x)加以修正，目的是让修正后的算子能保持线性函数.

引理2对(2)式给出的算子有

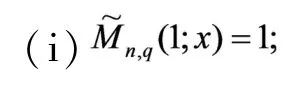
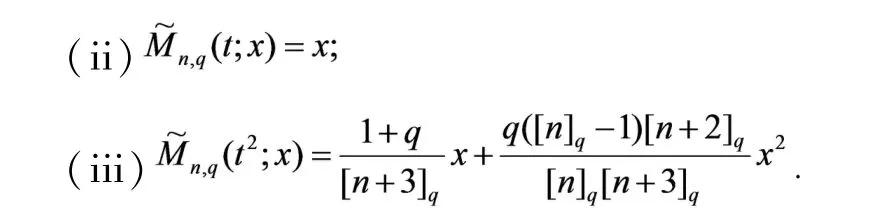
证明根据(2)式给出的定义，类似于文献[11]中引理2的定理，易得所述的结果.

引理3对(2)式给出的算子，有

证明(i)由引理2知，

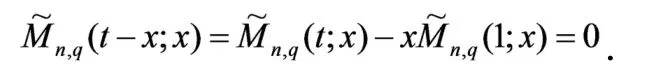
引理4对(2)式给出的算子，有

证明由算子的定义及引理2可得，

3 主要结果及其证明

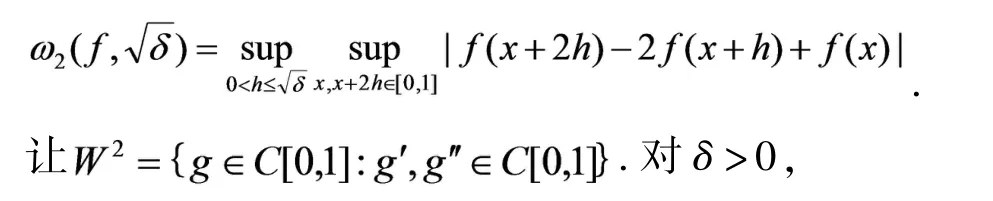
f∈C[0，1]，Peetre’sK-泛函定义如下:

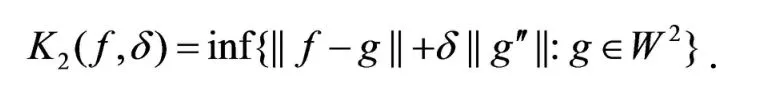
对f∈C[0，1]，从文献[14]的定理2.4可知，存在一个常数C，使得

定理1设qn∈(0，1)，则对任意的f∈C[0，1]，算子列在[0，1]上一致收敛于f，当且仅当

证明让qn∈(0，1)且由文献[15]可得，.因 此，由 引 理2和 引 理3知，对有由文献[16]Bohman-Korovich定理知，在[0，1]上一致收敛于f.

反过来，若对f∈C[0，1]，算子列在

[0，1]上一致收敛于f，则实事上，若不然，注意到，则必存在一个子列，使得，这样.从而.这表明算子列在[0，1]上非一致收敛于f，与已知矛盾.因此定理证毕.

2.2.6.3 发病条件。土壤温度和含水量是影响光叶紫花苕斑枯病2个主要的环境因素。该病的最适生长温度为25～30 ℃。春旱、秋涝，发病较严重。

定理2设

，则

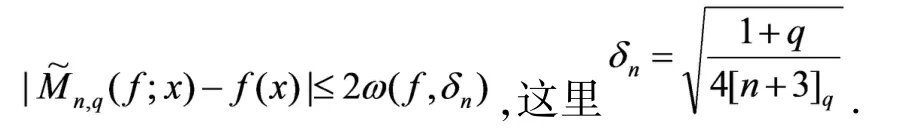
证明由引理2可得，

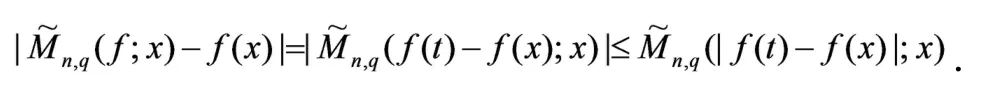
因为对x，t∈[0，1]及任意的δ＞0，有｜f(t)-f(x)｜所以，

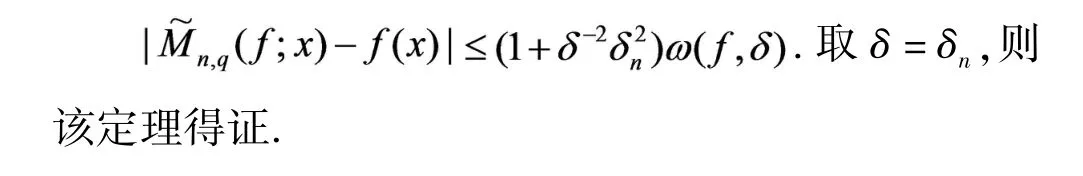
推论1设M＞0，0＜α＜1，q∈(0，1)，在[0，1]上则

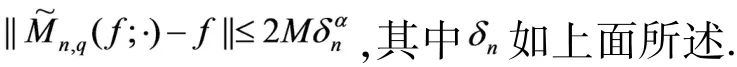
证明让，在，则有对 任 意 的因为等价于因此，由定理2知，对x∈[0，1]有从而有

定理3 设，则

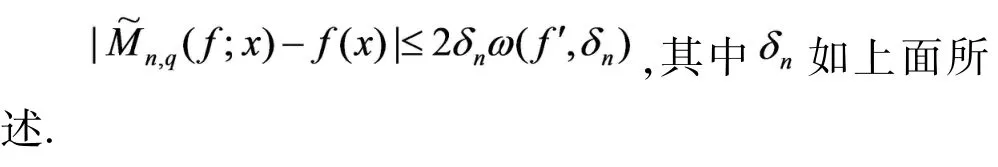
证明让f∈C[0，1]，则对任意的x，t∈[0，1]有所以，对任意的，有

由Cauchy-Schwarz不等式及引理2知，

因此，

于是，由引理2和引理3可得，

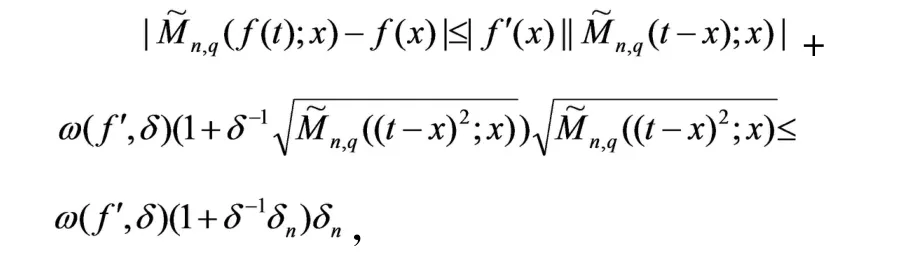
定理4设则必存在某个常数C＞0，使得

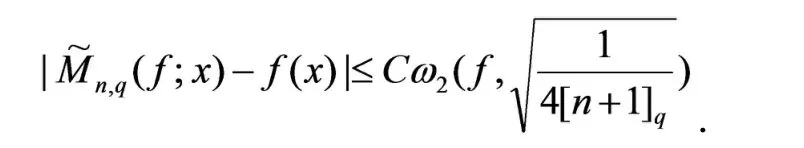
证明让g∈W2.对x，t∈[0，1]，由泰勒公式知，.因此，由引理2和引理3可得，

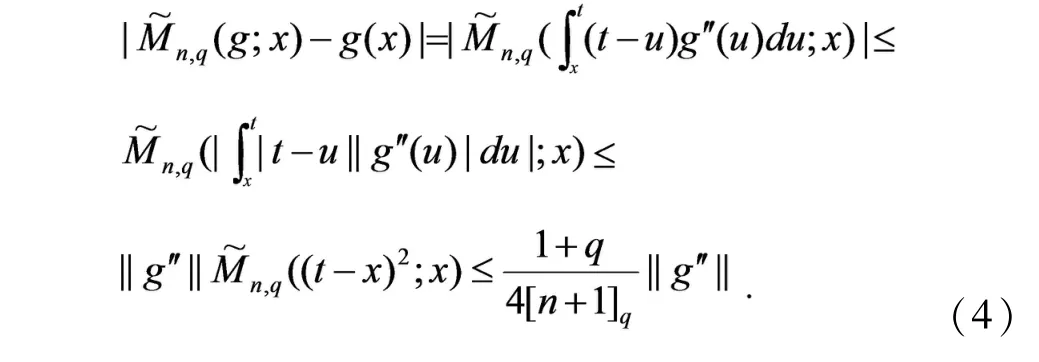
对f∈C[0，1]，因为(g(x)-f(x))，所以，基于不等式(4)，并结合引理2，引理3及引理4，可得

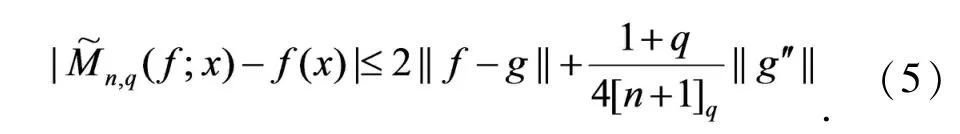
对不等式(5)的右边关于g∈W2取下确界，可得，因此，由(3)式知，必存在一个常数C＞0，使得该定理得证.