多孔端面液膜机械密封性能计算软件开发

刘 存

(中国石化海南炼油化工有限公司 海南儋州 578101)

随着石油化工行业中工况条件的越加苛刻，对机械密封的使用也提出了更高的要求。在某些特殊工况条件下，接触式机械密封由于端面的磨损，使用寿命和安全性难以满足要求[1-2]。在密封端面通过激光加工技术改变形貌提高密封的润滑特性，可以达到减小端面间摩擦的效果。多孔端面机械密封就是其中一种新型流体动压型机械密封，该类密封拥有普通机械密封无法比拟的优点[3-7]。

对于机械密封工程应用计算分析，为使计算结果具有更高的专业性与准确性，参照相关实验数据，在商业软件平台进行密封计算软件的开发方式较为可靠。相关计算软件已在干气密封的槽型结构优化设计、液膜密封性能计算方面得到应用[8-9]，节省大量时间与设计成本。

本文作者以多孔端面液膜机械密封为研究对象，分析了几何参数和工况参数对密封性能的影响规律，在MATLAB开发了相应的性能计算软件，为工程应用提供了参考。

1 计算模型

1.1 几何模型

多孔端面机械密封的端面如图1所示，密封端面上采用激光加工出圆形微孔。当密封运转时每个微孔的周边就会产生流体动压效应，从而使端面保持分离。当密封端面间的润滑介质减少时，微孔可以存储润滑剂进行补偿，从而改善密封端面的摩擦状态[10-13]。

微孔沿密封面周向呈等间距对称分布，由于结构对称，因此以虚线内的一个孔栏为研究对象。图中h0为非孔区的液膜厚度，hg为孔的最大深度，孔为球形结构，液膜厚度在端面的表达式为

(1)

1.2 控制方程

为了简化数值计算，假设密封端面非接触运转；压力在厚度方向没有梯度变换；流体为黏度不变的牛顿流体；端面间的相对滑动速度保持恒定。对Navier-Stokes(N-S)方程进行简化可以得到不可压缩流体在稳态层流条件下雷诺方程[1-2]，其极坐标形式[7]如下：

(2)

式中：h为流体膜的厚度；p为流体的压力；μ为流体的动力黏度；ρ为流体密度；ω为密封环角速度；r,θ为极半径和极角。

由于孔栏具有重复性，因此可只对一个孔栏进行求解。求解的基本边界条件为

(1)强制性边界条件

(3)

(2)周期性边界条件

p(r,θ1)=p(r,θ2)

(4)

1.3 控制方程的数值求解

采用有限差分法对雷诺方程进行求解[11-15]。图2所示为有限差分法的控制体积图，根据LEBECK[7]的研究结果，极坐标下雷诺方程的有限差分表达式如式(5)所示，极坐标下节点和控制体积如图2所示。

hi+1/2,j)=0

(5)

将式(4)写为式(5)的形式

Ai,jpi,j-Bi,jpi-1,j-Ci,jpi+1,j-Di,jpi,j-1-Ei,jpi,j+1-Fi,j=0

(6)

式中：Ai,j、Bi,j、Ci,j、Di,j、Ei,j、Fi,j为系数。

节点在r=ri与r=ro处的压力已知，节点在θ=θ1与θ=θ2处的压力相等。端面压力采用逐次超松弛迭代求解，迭代公式为

(7)

式(8)为迭代过程的结束条件，通过最终的pi,j结果得到密封端面压力。

(8)

1.4 密封性能参数

当密封端面计算完成之后，可以获得性能参数包括开启力、液膜刚度、泄漏量及摩擦扭矩。相关公式[7]如下。

(1)开启力

将所计算的液膜压力分布沿整个计算区域积分，再乘以密封槽个数Ng可得开启力：

(9)

(2)液膜刚度

密封处于稳态时液膜厚度为h0，轴向扰动Δh对应的开启力变化为ΔFz，膜刚度为

(10)

(3)端面摩擦力

由于径向流动相对于周向剪切流很小，因此在计算密封端面摩擦力时可忽略不计，则摩擦扭矩：

(11)

(4)泄漏率

密封的泄漏率采用下式进行计算：

(12)

2 计算软件的开发

2.1 软件的设计

为了方便工程人员进行使用，在第1节算法的基础上开发了一个多孔端面机械密封性能计算软件。开发工具采用MATLAB[16-18]，通过面向对象的设计方法进行程序编写，方便添加新的功能与程序维护。将共有的结构参数、操作参数、物性参数封装到基类MechSealBase中，然后派生出LSTGroove类。图3所示为软件的类图结构，软件的总体框架如图4所示。图5所示为软件的操作界面。

2.2 软件的应用及验证

采用表1中的参数，应用所开发的软件进行分析。图6所示为端面的几何结构。

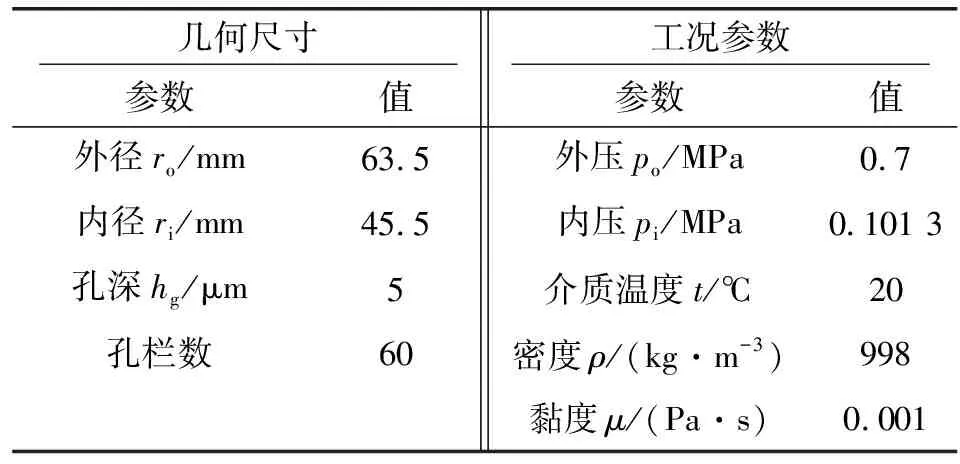
表1 密封端面几何尺寸及工况参数

图7所示为一个周期内的网格划分，图8所示为其压力分布。当密封环转动时，高压侧流体进入端面开孔，流体在切向剪切力的作用下在孔内流动，每一个孔相当于一个滑动轴承，在孔上方及其周边产生流体动压力，形成流体动压效应。在孔区和非孔区的收敛区域形成压力最高点，在发散区压力迅速下降，形成压力最低点。

为了验证计算数据的准确性，对软件计算的摩擦扭矩结果与文献[19]的试验结果进行对比，如图9所示。文献中采用了未开槽环与开槽环2种结构，开槽环槽深为40 μm，圆形织构直径为2 mm，油压为0.15 MPa。软件计算得到的摩擦扭矩曲线与文献中试验得到的摩擦扭矩曲线趋势一致，最大差值0.8 N·m左右，误差比例为17%。因理论模型、实验条件和几何结构数据存在误差，计算结果与文献结果存在一定误差，但数据在同一数量级，计算精度满足使用要求。

2.3 计算结果与讨论

采用开发的软件对表1给出的机械密封的端面开启力、液膜刚度、泄漏率、摩擦扭矩进行计算，探讨孔深、非孔区液膜厚度对密封性能参数的影响。

2.3.1 孔深对密封性能参数的影响

图10给出在孔径不变、非孔区深度不变，不同转速下孔深对密封性能参数的影响，其中包含开启力、液膜刚度、泄漏率、摩擦扭矩。可以看出，随着孔深的增加，开启力、液膜刚度、摩擦扭矩逐渐降低，原因是流体动压效应增加的趋势小于孔内流体静压的增加趋势，因此开启力减小。随着孔深度的增加，泄漏量呈现出缓慢增加的趋势。

2.3.2 非孔区液膜厚度对性能参数的影响

在孔径一定、孔深不变，非空区液膜厚度对性能的影响如图11所示。随着液膜厚度的增加，开启力、液膜刚度会出现一个峰值，然后逐渐降低；当膜厚超过7 μm之后，开启力、液膜刚度变化幅度微小，且各个转速对应的值趋于一致。这是由于液膜厚度的增加，流体的动压效应逐渐降低，导致液膜承载能力降低。随液膜厚度的增加，泄漏量在一定范围内波动，但是总体呈上升趋势，液膜厚度较大时，泄漏量增加趋势变缓慢。

3 结论

建立多孔端面机械密封的计算模型，给出密封性能的有限差分求解方法。采用面向对象的程序设计方法，通过Matlab GUI编制求解多孔端面机械密封性能的计算软件，该软件能够实现端面开启力、液膜刚度、泄漏率、摩擦扭矩的计算，并且二维、三维可视化效果较好，方便工程人员的使用。