倾斜射流撞壁实验研究及液膜几何参数建模
唐亮,胡锦华,刘计武,李平,周立新,杨宝娥
1.西安航天动力研究所 液体火箭发动机技术重点实验室,西安 710100 2.航天推进技术研究院,西安 710100
倾斜射流撞壁形成液膜在很多领域具有应用,比如液体火箭发动机中的液膜冷却,射流撞壁雾化[1-3]以及清洁[4-5]等。液膜冷却在液体火箭发动机中应用广泛[6-7],一般是轨姿控发动机的主要冷却方式,国外的R-4D轨姿控发动机以及国内490 N轨姿控发动机均用到液膜冷却技术。如果液膜冷却不合理,一方面会使发动机面临烧蚀风险,另一方面可能造成推进剂浪费,影响发动机比冲。因此合理设置发动机的液膜冷却是提高发动机热防护可靠性,延长发动机寿命的重要手段[8]。尤其对于轨姿控发动机,受限于推进剂流量较小,用于冷却的射流孔数量较少且都间隔较远,射流撞壁形成的液膜能否沿推力室周向完全覆盖壁面,以及覆盖区域的大小,这是液膜冷却设计中非常关心的问题,因此有必要对射流撞壁后形成的液膜几何外形加深认识。当前液膜冷却设计中比较依赖于经验和实验,建立射流撞壁后液膜的几何参数模型,有利于在液膜冷却设计中根据射流参数估计液膜几何形态,减小设计中对实验和经验的依赖。
一般而言,射流撞击壁面所形成的液膜形态受到多种因素的影响,在射流流量、流体物性、射流倾角、液体与壁面的接触角等因素的影响下,射流撞壁后会有不同的形态,比如向四周铺展并形成水跃、辫状流、撞壁后反弹、先铺展后破碎等[9]。相比于液滴撞壁[10-14],国内外针对射流撞击壁面的实验研究相对较少。Kibar等[9]开展了倾斜射流撞击竖直疏水壁面的实验研究,发现液膜铺展面积随着接触角的增大而减小,并从实验中揭示了壁面接触角、射流倾角、射流韦伯数对射流撞壁反弹的影响。林庆国[15]进行了射流撞壁的实验研究,观察了射流孔径、射流速度、射流倾角以及壁面曲率等因素对液膜形态的影响规律,并测量了不同截面处液膜厚度规律,认为射流倾角是影响液膜形态的关键因素。Ryan和William[16]对射流撞壁后的液膜分布进行研究,实验展示了多个小倾角下的液膜铺展形态,并研究了在不同倾角下最大液膜宽度与射流速度之间的关系。
在射流撞壁理论研究方面,Watson[17]最早建立了射流垂直撞击水平壁面后的液膜厚度分布模型,模型中考虑到了液膜流动分别为层流和湍流的情况。Kate等[18]研究了不同射流倾角下圆柱射流撞击水平壁面所形成的水跃现象,通过理论分析得到了水跃产生的位置,理论预测的水跃位置与实验吻合较好。另外,Kate等[19]也对射流撞击匀速运动的水平壁面所形成的水跃现象进行了理论研究,对水平壁面运动情况下的射流速度和射流倾角进行适当修正后,类比为射流撞击固定水平壁面进行分析,得到的理论结果与实验结果吻合较好。Inamura等[20]为了得到倾斜射流撞击壁面后的液膜厚度,在Hasson和Peck[21]提出的假设的基础上,考虑到液膜在铺展过程中层流边界层的发展,推导得到了倾斜射流撞壁后的液膜厚度分布模型。之后,Inamura等将这一模型进一步推广,对模型进行修正进而建立了射流撞击曲壁以后的液膜厚度分布模型[22]。Mertens等[23]对辫状流进行了理论研究,通过建模能够较为准确地描述辫状流的形成过程,揭示了在液膜表面张力和惯性力的作用下形成了辫状流。Wilson等[5]基于惯性力与表面张力的平衡,并考虑到壁面接触角的影响,建立了一套模型,能够较为准确地预测液膜径向铺展区域的半径。Wang等[24]建立了半经验的模型来研究射流速度、黏性、射流倾角等因素对液膜形态的影响,模型的计算结果与实验结果吻合较好。
对于射流撞壁铺展形成的液膜而言,有多个关键的几何参数可以描述液膜的特征,比如液膜长宽比、液膜最大宽度、液膜最大宽度距撞击点的距离等。目前对这些参数的定量研究相对较少,本文将在这方面开展理论研究工作,并通过射流撞击竖直壁面的实验研究,获取不同工况下的液膜形态,提取出液膜的关键几何参数;从几条假设出发,建立液膜长宽比的理论表达式,发现液膜最大宽度位置与对称面的夹角近似等于射流倾角这一结论;通过理论分析,得到半经验的液膜宽度的表达式;根据液膜参数间的几何关系,得到液膜的长度及液膜最大宽度距离撞击点的距离的表达式。计算表明,建立的液膜几何参数表达式计算结果均与实验结果吻合较好。应用本文建模获取的液膜几何参数的表达式,可以为液膜冷却的工程设计提供一定的指导。
1 射流撞壁实验
1.1 实验方法

图1 实验装置Fig.1 Experimental setup
壁面采用透明的树脂平板,经测定,水在实验中所采用树脂平板上的平衡接触角为73°。实验加工了8只喷嘴,喷嘴截面如图2所示,dj为射流孔径,Lh为射流孔长度,α为射流倾角。8只喷嘴的射流孔径从0.3~1.0 mm变化,长径比Lh/dj均为10,并在射流孔入口处加工了45°倒角,喷头材质为不锈钢,实验中的喷嘴安装于喷杆之中,喷杆可以沿着角度调节盘转动,从而控制射流倾角,实验中,喷嘴与竖直平板夹角的误差不超过1°。喷杆虽然可以通过前后伸缩控制射流出口距壁面的距离,但是受限于喷嘴及其附属结构自身的结构尺寸,喷嘴出口实际上与壁面是有一定距离的,并且在实验过程中,喷嘴结构不能紧贴壁面,与壁面之间需留有空隙。另一方面,在实验中需要尽量缩短射流出口与壁面之间的距离。在综合考虑之下,在实验中保持喷嘴出口与壁面之间的距离为10 mm。即在图2中,射流中心O1与竖直平板的距离为10 mm。

图2 喷嘴截面及尺寸Fig.2 Cross-sectional view and size of injector
在实验中,射流孔径、射流倾角、射流速度这3个因素可以进行调节,其中射流速度是根据流量及孔径计算得到的。针对轨姿控发动机内的液膜形成方式,开展射流撞壁的实验研究,以水作为实验液体,采用的射流孔直径变化从0.3~1.0 mm,射流倾角变化从10°~40°,射流速度变化范围从5~20 m/s。通过高速摄影拍摄,获得了100多组有效工况下的液膜铺展图像。实验中不同工况对应的各参数取值如表1所示。

表1 实验射流条件Table 1 Experimental jet conditions
1.2 实验结果
从实验中可以观察到典型的液膜形态,如图3 所示:射流撞击壁面以后,以撞击点为中心向四周铺展,然后液膜汇入边缘的跃起区域。液膜存在外边界与内边界,其中外边界是液膜外缘和壁面的分界线,而内边界为薄膜区与边缘跃起区的边界。可以看出,随着液膜向下游流动,液膜的宽度先增大后减小,存在一个最大宽度。从撞击点到液膜最大宽度位置,液体的惯性力克服表面张力致使液膜宽度不断增大,而在之后的位置,在液体的表面张力作用下,液膜宽度不断变小,最后液膜于一点汇集。射流撞壁铺展过程中,所受到的力十分复杂,虽然射流撞击竖直平板,在液膜铺展过程中一直受到重力作用,但在本文实验中弗劳德数Fr≫1,因此实验中液膜铺展是由惯性力主导的,重力的影响相对较小,在后续建模过程中可忽略重力的影响。
同时可以定性观察到液膜形态随着射流条件变化的趋势。图4为孔径为0.4 mm、射流速度15 m/s时,不同射流倾角对应的液膜形态。可以看出,随着射流倾角增大,液膜长度减小,宽度增大。图5是射流倾角为20°、射流速度15 m/s时,不同射流孔径对应的液膜形态。可以看出,随着孔径增大,液膜长度和宽度均增大。图6为孔径为0.4 mm、射流倾角为20°时,不同射流速度对应的液膜形态。可以看出,随着射流速度增大,液膜长度和宽度也均增大。

图3 典型液膜图像Fig.3 Typical liquid film image

图4 射流倾角对液膜形态的影响Fig.4 Effect of jet angle on liquid film shape

图5 射流孔径对液膜形态的影响Fig.5 Effect of jet diameter on liquid film shape

图6 射流速度对液膜形态的影响Fig.6 Effect of jet velocity on liquid film shape
1.3 液膜几何参数定义
从实验中提取液膜的几个关键几何参数,分别是液膜长度L、液膜最大宽度W以及液膜最大宽度距撞击点的距离H。这3个参数的提取方法如图7所示,液膜长度沿液膜流动方向在图片中提取,终止于液膜收缩成束的位置;液膜最大宽度取为对称轴两侧液膜边缘之间的最大距离。在提取过程中,取3次提取结果的平均值,以减小数据提取过程中的误差。

(1)
(2)
式中:RLW代表液膜的长宽比;αw代表液膜最大宽度位置与对称面的夹角。如图7所示,图中标注出了αw所代表的角度。

图7 液膜几何参数Fig.7 Geometrical parameters of liquid film
2 液膜几何参数建模
液膜的几何参数有液膜长宽比、液膜宽度、液膜长度、液膜最大宽度位置与对称面的夹角αw、最大宽度距撞击点的距离这几个参数,且均是无量纲参数。下文通过建模分别求得这几个参数的表达式。
2.1 液膜长宽比
液膜长宽比是衡量液膜形态的重要参数,液膜长宽比的影响因素也较为复杂,从图4~图6可以看出,影响液膜长宽比最重要的射流参数是射流的倾角。在液膜长宽比建模之前,引入以下几个主要的假设:
同时,既然材料价格上涨了,附属工程或措施项目成本也必然会增加,如供风、供水管路、供电线路、辅助加工厂等,临时办公及生活用房、砂石料系统、混凝土生产系统等更是与此直接相关。
1) 射流为具有均匀速度的圆柱射流。
2) 射流撞壁引起的飞溅量可以忽略。
3) 射流撞击壁面过程中没有能量损失。
4) 忽略重力的影响。
5) 倾斜射流可以分解为垂直壁面的射流形成的流动叠加一个平行于壁面的流动。
6) 液膜的长宽比取决于长度方向的最大速度和宽度方向的最大速度之比。

图8 射流撞壁等效原理Fig.8 Equivalent principle of jet impinging onto a wall
对于液膜长宽比这一无量纲的参数,采用理论建模的方式,对其进行分析。图8显示了速度大小为uj的倾斜射流以角度α撞击到壁面上,倾斜射流可以分解为垂直壁面的射流形成的流动叠加一个平行于壁面的流动。即倾角为α的倾斜射流撞壁可以被等效为:射流以速度uv垂直撞壁,然后在与壁面平行方向叠加一个速度ut,其中uv=uj·sinα,ut=uj·cosα。如图8所示,液膜关于x轴对称,y轴垂直于x轴。垂直壁面的射流撞击壁面后,假设撞击过程没有能量损失,则流动依旧以速度uv向四周流动。在此流动的基础上,叠加一个流动速度ut,则沿着x轴方向的最大流速变为uv+ut,沿y轴方向的最大流动速度依旧为uv。由于液膜的铺开过程是由惯性力驱动的,因此假设液膜在某个方向上流动的最大距离由这个方向上的初始速度决定,则长宽比等于长度方向上的最大速度与宽度方向上的最大速度之比,即
(3)
为了验证液膜长宽比关系式的正确性,对比液膜长宽比的理论预测结果与实验结果,如图9所示。可以看出,理论预测的长宽比与实验中测

图9 液膜长宽比实验结果与理论预测结果对比Fig.9 Comparison between experimental and theoretical results of aspect ratio of liquid film
量得到的长宽比趋势上吻合较好,实验数据点散布在理论预测曲线的两侧。长宽比的理论模型表明,当α趋于90°时,长宽比趋于1,当α趋于0°时,长宽比趋于无穷大。在本文实验中,20°倾角下,不同射流速度、射流孔径下的液膜长宽比分布在 3~4.8(见图9),而1+cotα的预测结果为3.75, 1+cotα的预测结果与各工况下实验结果的最大误差不超过25%。事实上,虽然射流倾角是影响液膜长宽比最为重要的因素,但在同一倾角下,包括射流速度、射流孔径等其他因素也会导致液膜长宽比有所不同,这些因素是模型中所不能考虑到的。总体而言,虽然1+cotα预测的长宽比和某一个具体工况下可能有一定的误差,但在仅考虑射流倾角的影响下,1+cotα可以较好地描述射流撞壁以后长宽比随射流倾角α的变化趋势。
2.2 夹 角
液膜最大宽度位置与对称面的夹角αw也可通过上面的理论分析得到。如图8所示,根据射流撞壁后流动等效叠加,αw是边长分别为uv、ut、uj的直角三角形中的一个锐角,大小恰好等于射流倾角,即
αw=α
(4)
图10显示了实验测量得到的αw随倾角α的变化关系,从图中可以看到,αw基本与α相等,绝大多数点的误差在20%之内,表明理论分析得到αw=α的结论是可信的。需要说明的是,随着射流倾角α由10°增加到40°,实验测得的αw的平均值是逐渐偏离理论值α的,且αw的平均值小于α。但总体而言,当射流倾角在40°以内时,式(4)的准确性还是较高的。

图10 夹角αw的实验结果与理论预测结果对比Fig.10 Comparison between experimental results and theoretical results of angle αw
2.3 液膜最大宽度
Wilson等[5]根据惯性力与张力的平衡推导得到了射流垂直撞击竖直壁面形成的液膜内边缘半径R,图11为对应的实验图片以及流动结构示意图,表明射流撞击壁面后形成近似圆形的液膜边缘结构,Rc为液膜的外边缘半径;在重力作用下,流动从液膜下方流出,液膜内边缘半径R的表达式为
(5)
式中:ρ为液体密度;Q为体积流率;μ为液体黏性;δ为液体表面张力;β为壁面接触角。
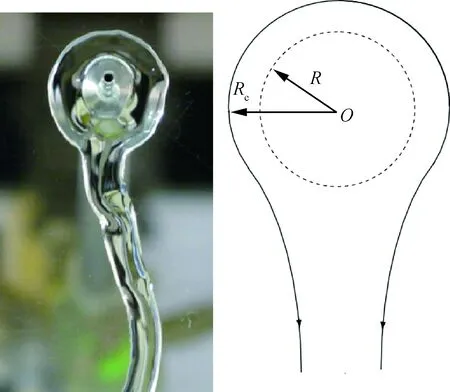
图11 射流垂直撞击竖直壁面所形成的液膜[5]Fig.11 Liquid film formed by vertical jet impinging onto wall[5]
对于倾斜射流撞壁形成的液膜宽度,可以借鉴Wilson得到的结论。Wilson建立的式(5)中,并未包含重力的影响,本文在建模获取液膜最大宽度的过程中同样不考虑重力的影响。液膜宽度与垂直壁面方向的惯性力相关,将倾斜射流的流动进行分解,则可假定液膜宽度与射流垂直撞壁形成的液膜宽度相当,即可认为倾斜射流撞壁形成的液膜宽度W近似等于2Rc,即W=2C·Rc,C为复合修正系数。而Rc>R,可令C1=Rc/R,则W=2C1C2R,C2代表对其他误差的修正,其中C=C1C2,则对于倾角为α的射流撞击竖直壁面形成的液膜,其最大宽度可以写为
(6)
式中:Q·sinα表示Q在垂直壁面方向的分量,从式(6)可以看出,液膜宽度受体积流率Q、射流倾角α、射流的密度、黏性、表面张力以及液体与壁面接触角β的影响。以射流直径dj为长度尺度、射流速度uj为速度尺度对式(6)进行无量纲化,则可以得到
(7)

(8)
从式(8)可以看出,倾斜射流撞壁形成的液膜宽度的影响因素有Rev、Wev以及接触角β。液膜宽度随着Rev和Wev的增大而增大,随着接触角β的增大而减小。图12显示了本文实验中无量纲液膜宽度与Rev和Wev的关系,由于实验是在固定的接触角下进行的,因此实验中接触角对液膜宽度的影响可以认为是个常值。另外,在不同射流条件下C1是不同的,C1的范围一般在1~2,而C2的数值应该在1附近。为了获得较为准确的关联式,根据实验数据对C1与C2的乘积进行拟合,也就是对C进行拟合,可以得到C=1.68, 此时,式(8)预测的液膜宽度与实验结果的对比如图13 所示。可以发现,所有点的误差都在20%以内,显示出式(8)的预测具有较高的准确性。另外,图14中显示了在本文实验条件下,式(8)预测的液膜宽度与Rev和Wev的关系,液膜宽度随着Rev和Wev的增大而单调增大。而且从图12和图14均可以看出,当Rev和Wev均较小时,无量纲液膜宽度随Rev和Wev的增长而快速增长,而当Rev和Wev较大时,无量纲液膜宽度随Rev和Wev的增长逐渐放缓。

图12 实验测得的液膜宽度Fig.12 Measured liquid film width

图13 液膜最大宽度预测结果与实验结果对比Fig.13 Comparison between experimental and predicted results of liquid film maximum width
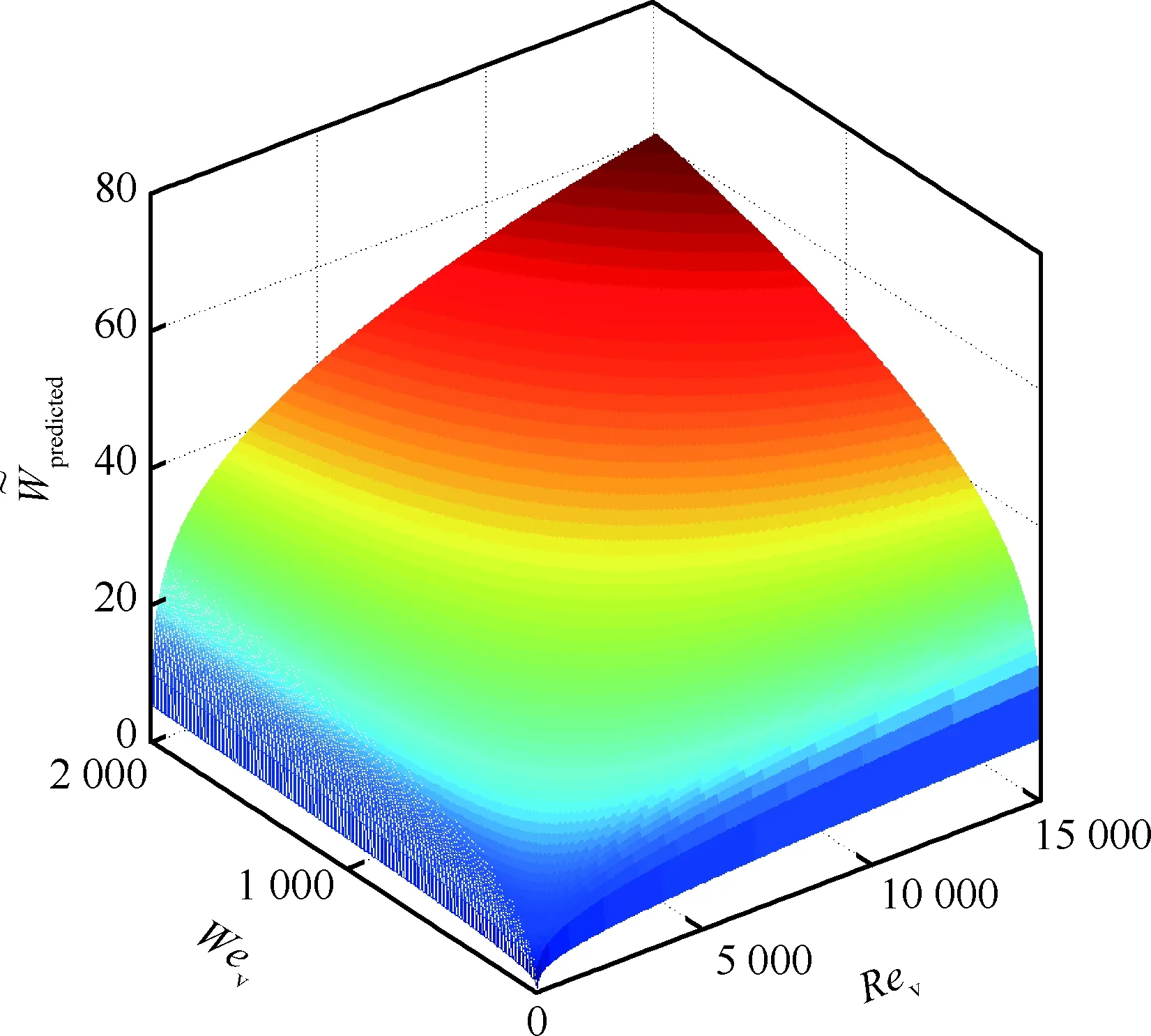
图14 预测液膜最大宽度与Rev、Wev之间的关系Fig.14 Relationship between predicted liquid film maximum width and Rev and Wev
2.4 液膜长度及最大宽度位置距撞击点的距离

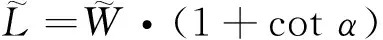
(9)
(10)
通过与实验结果进行比较,对式(9)和式(10)进行验证。图15显示了液膜长度实验值与预测值的比较,图16显示了液膜最大宽度位置距射流撞壁点距离实验值与预测值的比较,大多数实验点预测值与理论值的误差在20%以内,证明了模型的准确性。

图15 液膜长度预测值与实验结果对比Fig.15 Comparison between experimental and predicted results of liquid film length

图预测值与实验结果对比Fig.16 Comparison between experimental and
3 结 论
开展了倾斜射流撞壁实验研究,改变射流孔径、射流速度、射流倾角等因素,观察到射流撞壁以后的液膜形态变化规律并建模获取液膜几何参数的表达式,得到以下结论:
1) 随着射流倾角增大,液膜长度减小,宽度增大;随着射流孔径和射流速度分别增大,液膜长度和宽度均会增大。
2) 建模得到液膜的长宽比近似等于1+cotα,液膜最大宽度位置与对称面的夹角近似等于射流倾角α,与实验结果的对比验证了模型的准确性。
3) 通过建模得到了液膜宽度的半经验表达式,进一步根据几何关系得到了液膜最大宽度位置距撞击点的距离以及液膜长度的表达式。表达式预测结果与实验结果吻合较好,绝大多数实验点的误差在20%以内,验证了模型的准确性。

