轴箱内、外置车辆轮轴弯曲对轮轨接触的影响
方凌昊,关庆华,温泽峰
(西南交通大学牵引动力国家重点实验室,四川成都,610031)
轮轨接触点位置计算是研究轮轨接触特性的首要问题。在对铁路车辆动力学性能进行仿真计算时,通常把轮对和钢轨考虑成刚体,然而这只适用于低频的情况。轮对的弹性变形会导致车轮踏面和钢轨踏面之间的相对位置发生变化,对轮轨接触点位置、动力学性能产生一定影响[1−4]。近年来,轴箱内置车辆发展迅速[5],与轴箱外置车辆相比,轴箱内置车辆具有较好的曲线通过能力和较小的轮轨磨耗。由于轴箱内、外置车辆的轴箱位置不同,轴箱内、外置车辆的轮轴具有不同的弯曲形式。为了更精确地研究轴箱内、外置车辆轮轨接触特点,需要考虑轮轴柔性的影响[6−7]。
高浩等[8]在传统迹线法[9]的基础上提出了一种考虑轮对弹性的轮轨接触点计算方法,弹性轮对模型采用离散的有限元模型,此方法需要扫描大量的节点,计算量较大。李国芳等[10]发现相对刚性轮对而言,考虑轮对柔性后车辆系统的运行安全性能有所提升。张宝安等[11]将车轴假设为铁木辛柯梁求解其变形信息,再利用轮轨接触几何关系,用解析的方法对约束方程进行求解。石俊杰等[12]把车轴简化为欧拉−伯努利梁,求解车轴运动微分方程以获得变形信息,再基于传统迹线法,求解变形后的轮轨接触几何参数。他们发现当轮对横移量较大时,轮对的结构柔性会导致轮轨接触参数发生明显变化。张剑等[13]通过轮轨接触和车辆动力学计算,分析了等效锥度对车辆临界速度和曲线通过性能的影响。卢萍等[14−16]采用Hertz接触理论和有限元模型求解轮轨接触应力,发现有限元较Hertz接触理论更能反映轮轨接触实际情况,但计算速度较慢。陶功权等[17]对比研究了CONTACT算法和三维轮轨接触有限元模型在接触应力计算上的区别。周志军等[18]研究了地铁车轮凹陷磨耗对踏面接触应力的影响。发现当车辆频繁地通过小半径曲线时,易在磨耗突变区造成较高的等效应力和等效塑性应变,导致轮缘根部表面材料产生剥离损伤。
上述研究的轮轨接触关系主要针对常规的车辆型式,而关于轴箱内、外置布置形式对轮轴弯曲以及轮轨接触特性影响的研究较少。事实上,轴箱内、外置车辆已经在我国部分地铁中采用,并列入了未来高速列车新型转向架的研究计划。张雄飞等[19]介绍了我国轴箱内、外置直线电机车辆转向架结构。许世杰等[20]对国内某直线电机地铁轴箱内、外置车辆出现的车轮踏面双光带现象进行研究,通过对比车轮廓形、钢轨廓形以及线路状况的测试结果,分析了车轮踏面双光带的可能成因。邓铁松等[21−23]对比轴箱内、外置直线电机地铁车辆过曲线时的轮对冲角、脱轨系数、轮轨横向力等,发现在不同的曲线半径和行车速度下轴箱内置车辆的曲线通过性比轴箱外置车辆的性能好。陈斌[24]根据现场测试结果,对比分析轴箱内、外置车辆车轮磨耗的特性,并且建立动力学模型,对实测轮轨廓形下的车辆动力学性能进行了仿真研究。因此,精确分析轴箱内、外置车辆的轮轨接触特性对掌握轴箱内、外置车辆动力学性能差异具有重要意义。为此,本文作者以我国轴箱外置和内置2种结构形式的地铁车辆为对象,建立轮轨接触三维有限元模型和考虑轮轴弯曲的轮轨空间接触模型,分析轴箱布置形式对轮轴弯曲、轮轨接触点位置、等效锥度以及接触应力的影响,以期为进一步研究轴箱内、外置车辆动力学提供参考。
1 轴箱内、外置车辆轮轨接触有限元模型
轴箱内置式和外置式车辆的结构简图如图1所示,轴箱内置转向架的轴箱位于车轮内侧,轴箱外置式转向架轴箱位于车轮外侧,相比而言,轴箱内置车辆一系簧横向跨距小、结构紧凑。2种轴箱布置形式的重要差异在于一系悬挂位置不同,这将导致车轴弯曲形态不同。
轴箱内、外置车辆三维轮轨接触有限元模型如图2所示。其中,用集中力F表示作用于轴箱的簧上载荷。2 种车型轮对均采用标准LM 型踏面,轮径为730 mm,无载荷时轮对内侧距为1 353 mm,轨距为1 435 mm,计算轨道长度为6 110 mm,轨底坡坡率为1/40。如图2(c)所示,单元网格类型采用八节点六面体单元,接触区域的网格长度为1 mm,泊松比为0.3,杨氏模量为205.9 GPa,轮轨间的摩擦因数为0.5。钢轨横向和纵向对称约束,垂向与轨道板弹性连接。在模型中轮对沿横向设定横移量,同时沿垂向调整轮对和钢轨之间的间隙,通过控制间隙误差限度使轮对和钢轨满足接触条件,保证轮轨接触求解过程完全收敛。
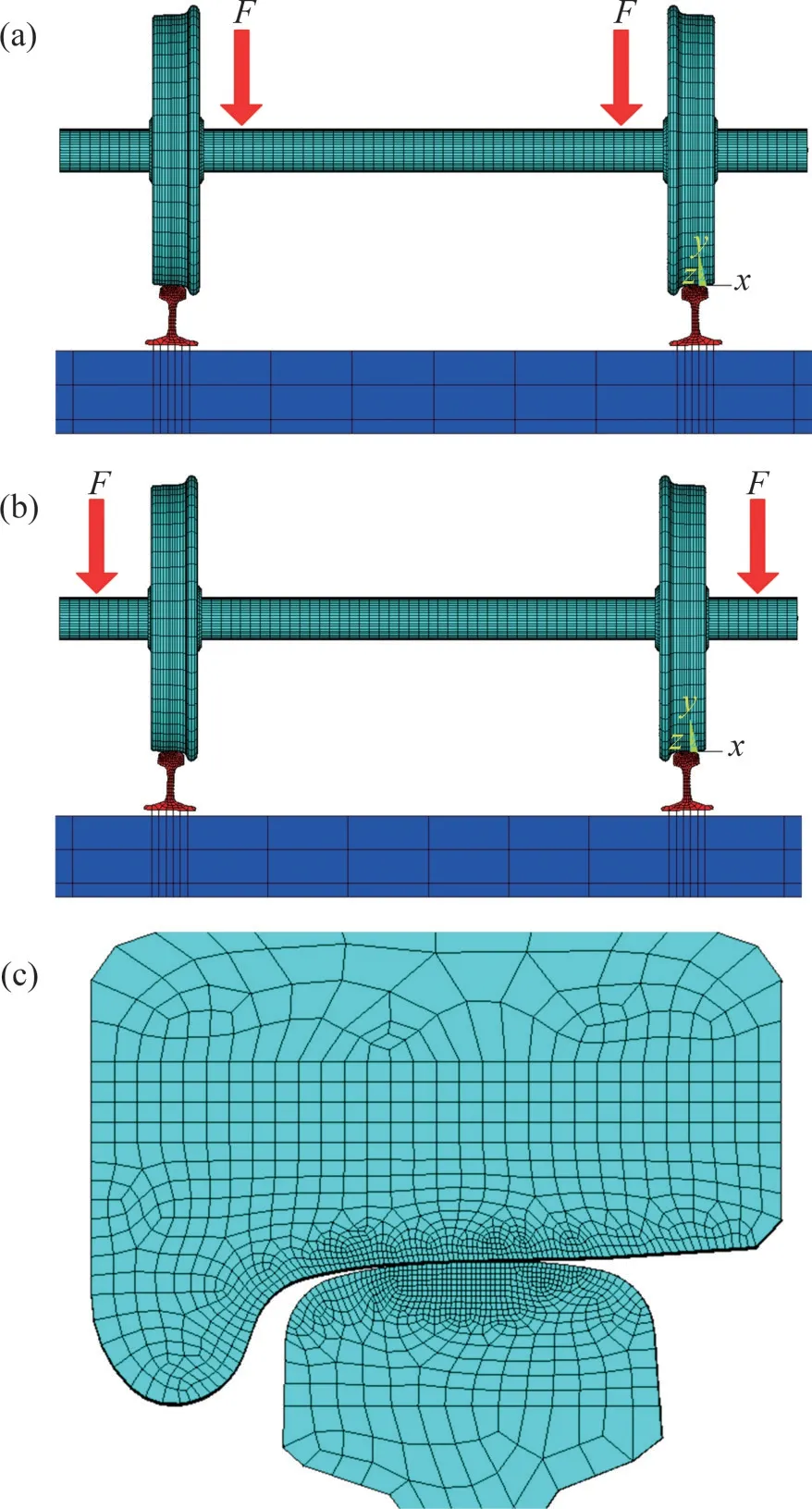
图2 三维弹性轮轨接触有限元模型Fig.2 Finite element model of three-dimensional elastic wheel-rail contact
2 轮轴弯曲对轮轨接触几何关系的影响
关于轮轴弯曲对轮轨接触几何关系的影响,将从轮轨接触点位置、滚动圆半径及等效锥度等方面进行分析。
2.1 轮轴弯曲对轮轨接触点位置的影响
由于轴箱位置不同导致在相同载荷的作用下,轴箱内、外置车辆轮轴弯曲变形具有不同的形式,如图3所示,轴箱内、外置车辆在运行时,在簧上载荷和轮轨载荷共同作用下,轴箱内置车辆的车轴会向下“凹陷”,轴箱外置车辆的车轴会向上“凸起”。当轮轴发生弯曲时,相对应的车轮踏面廓形也会产生旋转。采用图2所示轮对模型,施加约束后,由几何关系可得出,在施加载荷的情况下,名义滚动圆在垂直方向和水平方向的偏转角度相同,所以选择左侧名义滚动圆顶端节点,输出该节点的横向位移变化,横向位移放大100倍的计算结果如图3所示。
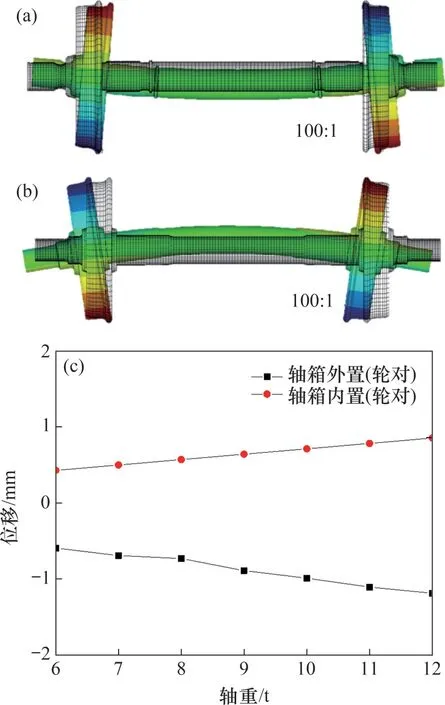
图3 轮轴弯曲变形计算结果Fig.3 Calculation results of wheelset bending deformation
从图3(c)可以得知,轴箱内置车辆的左侧名义滚动圆顶端节点的横移量要比轴箱外置车辆少28.27%,这表明几何和物理参数一致的轮对,轴箱内置车轴具有更良好的抵抗弯曲变形的能力。
图4所示为不同轴重下2种轮对的内侧距变化情况,图中红色虚线为轮对内侧距名义值。由图4可以看出:根据轴箱内、外置车轴弯曲特点,轴箱内置车辆的车轴线下方轮对内侧距增加,轴箱外置车辆的车轴线下方轮对内侧距减小,2种车型的内侧距变化量均不超过2 mm,轴箱内置车辆的轮对内侧距的变化量比轴箱外置车辆的变化量小。

图4 轴箱内、外置车辆轮对内侧距变化Fig.4 Variation of flange back-back distance of vehicles with inside and outside axle boxes
轴箱内、外置车辆的名义滚动圆直径为730 mm,轮轴弯曲后所选择的节点垂向位移和名义滚动圆直径相比可忽略不计。把所选择节点的横移量转换成偏角,结果如表1所示。

表1 不同轴重下名义滚动圆节点偏角Table 1 Deflection angle of nominal rolling circle node with different axle loads
对标准的LM踏面廓形进行旋转处理,旋转角度为表1中2 种车型对应的偏角,得到图5所示车轮廓形。位于正中间的黑色廓形为不考虑轴弯时的车轮廓形,显然,在考虑轮对轴弯后,轴箱内置车辆的车轮廓形相对偏向上方,轴箱外置车辆的车轮廓形相对偏向下方。
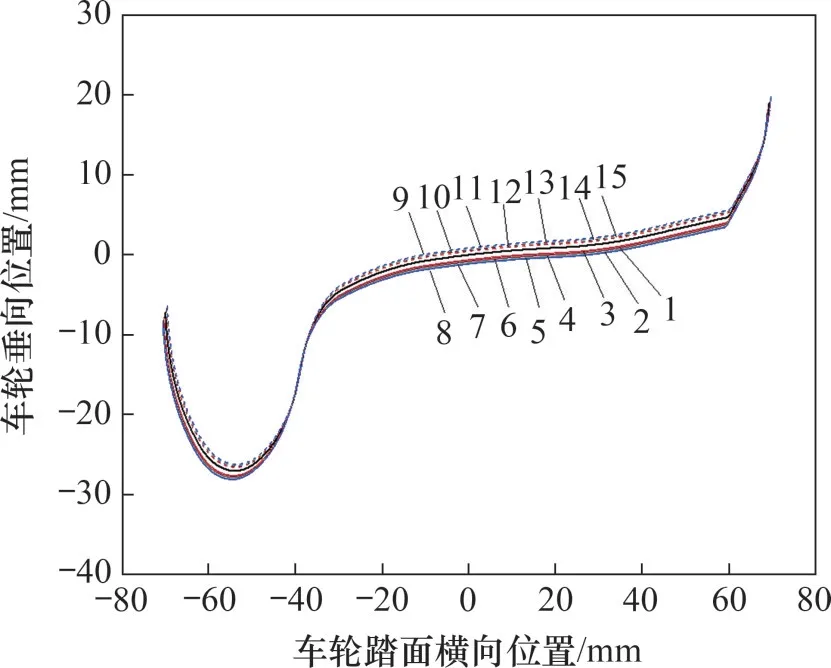
图5 考虑轮轴弯曲后2种车型对应车轮廓形Fig.5 Wheel profiles corresponding to two vehicle types under axle bending
选取标准LM 踏面分别与标准60 轨、实测钢轨匹配,利用改进的迹线法求解不同轮轴弯曲状态下的轮轨接触几何参数,计算结果如图6所示。当车轮横移量为[0,12]mm 时,不同轴重下计算得到的轮轨接触点对情况如表2所示。
图6中,黑色廓形为不考虑轴弯时的车轮廓形;红色为轴箱内置车辆的车轮廓形;蓝色为轴箱外置车辆的车轮廓形。从图6可以看出:当轮对横移量为[0,6)mm 和(9,12]mm 时,2 种车型轮轨接触点位置保持一致;分别以轴重为0,6 和12 t,横移量为6 mm 为例,轴箱内置车辆的轮轨接触点位于钢轨横向位置上的坐标分别为−22.90,−24.03和−25.26 mm;轴箱外置车辆的轮轨接触点位置分别为−22.90,−21.38和−19.17 mm。
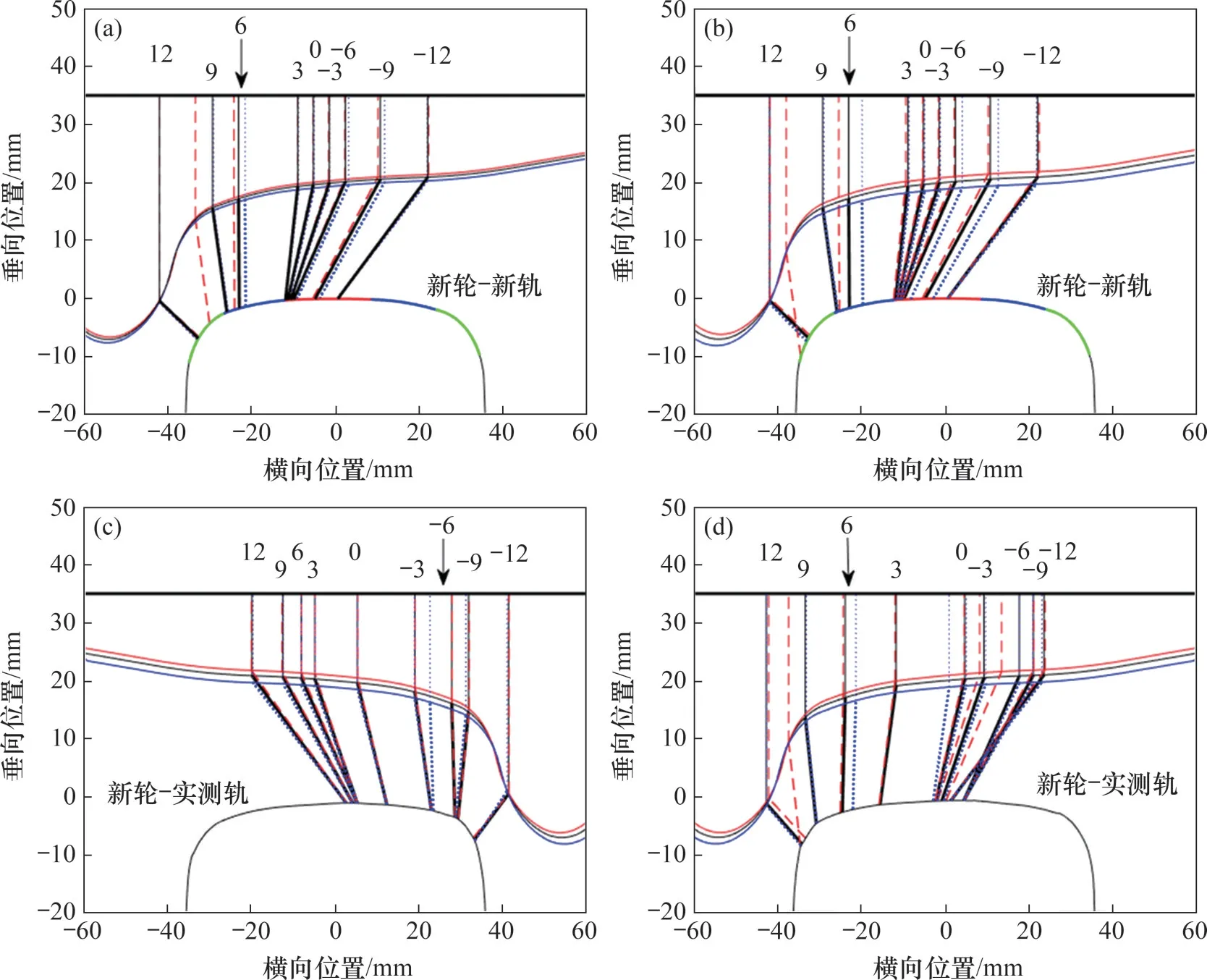
图6 不同工况下轮轨接触点对图Fig.6 Wheel-rail contact point diagrams at different conditions
由此可以看出,当轮对横移量为[0,6)mm和(9,12]mm 时,轴箱内、外置车辆的轮轨接触点位置基本不会发生变化;当轮对横移量位于[6,9]mm 之间时,2 种车型的轮轨接触点位置会发生变化,轴箱内置车辆的轮轨接触点位置更靠近轮缘和钢轨轨距角。可以看出,轴箱外置车辆相对于轴箱内置车辆在钢轨上的接触点位置往右侧移动了2.65~6.09 mm,因此,通过小半径曲线时,与轴箱外置车辆相比,轴箱内置车辆需要较小的轮对横移量。
2.2 轮轴弯曲对滚动圆半径差的影响
轮对沿钢轨向前滚动时,车轮和钢轨的接触点位置不断变化,车轮的滚动圆半径差也随之变化。图7所示为不考虑轴弯和考虑轴弯的轴箱内、外置车辆滚动圆半径差和轮对横移量之间的关系。从图7可以看出:当横移量为[−4,4]mm时,考虑轴弯的轴箱内、外置车轮滚动圆半径与不考虑轴弯的滚动圆半径差在数值上基本保持一致;当横移量为[−9,−4)mm和(4,9]mm时,滚动圆半径差缓慢增加;当横移量为[−12,−9)mm 和(9,12]mm时,滚动圆半径差变化迅速。

图7 滚动圆半径差与轮对横移量之间的关系Fig.7 Relationship between radius difference of rolling circle and wheelset lateral displacement
2.3 轮轴弯曲对等效锥度的影响
图8所示为不考虑轮轴弯时和考虑轮轴弯曲情况下,等效锥度随横移量变化的情况。从图8可以看出:当横移量为[0,3]mm时,轴箱内、外置车辆等效锥度基本相等,且数值均小于0.1;当横移量为[4,12]mm 时,在相同的横移量下,轴箱内置车辆等效锥度大,轴箱外置车辆等效锥度小。因此,从接触特性上看,通过曲线时,在同等横移量下,轴箱内置车辆的锥度更大,其曲线通过性能更好。
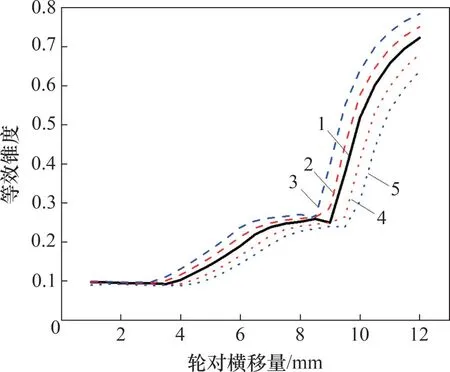
图8 等效锥度与轮对横移量之间的关系Fig.8 Relationship between equivalent conicity and the wheelset lateral displacement
3 轮轴弯曲对轮轨接触应力的影响
利用上述建立的考虑轮轨真实几何关系的三维轮轨接触有限元模型,计算轮对不同横移量下([0,6]mm)轴箱内、外置车辆轮轨接触斑面积、接触应力和Von-Mises等效应力。轮轨接触应力对轮轨磨耗和轮轨滚动接触疲劳影响较大,轮轨接触区域的材料屈服条件采用Von-Mises 屈服准则,屈服极限为615 MPa[18]。
3.1 Hertz接触理论
Hertz接触理论认为接触斑为椭圆形,在Hertz接触理论的假设条件下,接触斑内的法向压应力分布为

式中:x和y分别为沿椭圆长半轴和短半轴坐标;a和b分别为椭圆接触斑的长、短半轴长度,m;q0为接触斑上的最大接触压应力,Pa。
最大接触压应力q0为

式中:P为接触椭圆内法向合力,N。
椭圆接触斑的长半轴和短半轴分别为[25]:

式中:A和B为常数,取决于车轮和钢轨曲面的主曲率以及2个物体主曲率所对应主方向的夹角;m和n为系数,可直接查表得到;椭圆接触斑长、短半轴的方向由(B−A)/(A+B)来确定;G*为材料物理参数,

式中:E1和E2分别为车轮和钢轨的弹性模量;γ1和γ2分别为车轮和钢轨泊松比。
3.2 结果分析
分别采用Hertz 接触理论和有限元模型计算轴箱内、外置车辆在轮对不同横移量下的轮轨接触斑面积和接触应力。两者相比,Hertz 接触理论计算效率高,但Hertz接触理论建立在理想假设基础上,难以考虑实际廓形变化引起的非Hertz接触特征;通过有限元方法可以克服Hertz接触理论的不足。根据Hertz 接触理论计算结果可知,当轴箱内、外置车辆横移量为[0,12]mm 时,轮轨接触斑面积大小和接触应力如图9所示。从图9可以看出:当横移量为[0,4]mm 时,2 种车型的接触斑面积一致;当横移量为[5,12]mm 时,轴箱内置车辆的接触斑面积比轴箱外置车辆的接触斑面积小,这是因为当轮对横移量较大时,轴箱内置车辆的接触点位置更靠近轮缘,轮轨接触区域曲率增加,所以接触斑面积减小。
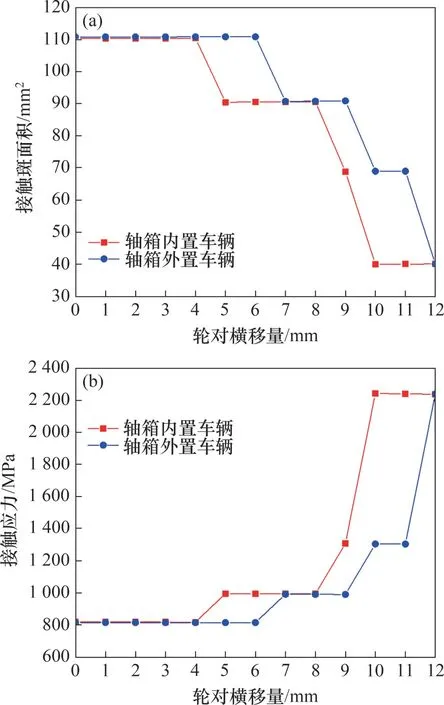
图9 Hertz接触理论计算结果Fig.9 Calculation results of Hertz contact theory
通过Hertz 接触理论计算得到的2 种车型在横移量为[0,6]mm 时的接触应力对比如表3所示。从表3可以看出:当横移量为[0,4]mm时,2种车型的接触应力保持一致;当横移量为[5,6]mm时,轴箱内置车辆的接触应力增大,这是因为此时轴箱内置车辆的接触面积减小,所以接触应力增大。

表3 轴箱内、外置车辆Hertz接触理论计算结果Table 3 Calculation results of vehicles with inside and outside axle boxes obtained by Hertz contact theory
通过有限元计算得到的不同横移量下轴箱内、外置车辆轮轨接触斑变化情况如图10所示,接触斑外圈的黑色椭圆为Hertz接触理论计算得到的接触斑。从图10可以看出:当横移量为[0,6]mm时,轴箱内、外置车辆的接触斑形状近似为椭圆形,2种方法计算得到的接触斑面积基本相等。当轴重为12 t、轮对横移量为6 mm 时,通过图 6(b)可以看出,轴箱内置车辆在钢轨上的接触点位置为−25.26 mm,ANSYS 计算得出的接触斑接触点位置为−24.02 mm,两者基本一致。

图10 轮轨接触斑和接触应力最大值Fig.10 Wheel-rail contact patches and maximum contact pressure
从图10(c)可以看出:当横移量为0 mm时,两者接触应力均达到最大,轴箱内置车辆接触应力为876 MPa,轴箱外置车辆接触应力为925 MPa。当横移量为[0,4]mm时,轴箱内置车辆接触应力最大值比轴箱外置车辆的最大值稍小;当横移量在[5,6]mm时,轴箱内置车辆接触应力最大值比轴箱外置车辆的稍大,这是因为当横移量为[4,12]mm 时,轴箱内置车辆的接触点位置相较于轴箱外置车辆偏向钢轨轨距角侧,接触位置处的钢轨和车轮曲率半径小,接触面积小,所以接触应力大。
图11所示为轴箱内、外置车辆轮对在不同横移量下,轮轨Von-Mises等效应力最大值的变化情况。从图11可以看出:轴箱内、外置车辆轮轨Von-Mises 等效应力在轮对横移量为0 mm 时的最大值最大,轴箱内置车辆的Von-Mises等效应力最大值为517 MPa;轴箱外置车辆为556 MPa,2 种车辆的轮轨Von-Mises等效应力最大值均比屈服极限低。
图12所示为轴箱内、外置车辆轴重为12 t,轮对横移量分别为0 mm和6 mm时的Von-Mises等效应力云图。由图12可以看出:相较于轴箱外置车辆,轴箱内置车辆的等效应力集中点向钢轨内侧偏移,位置更加靠近轮缘和轨距角。
4 结论
1)轴箱内、外置车辆在运行时,轴箱内置车辆的车轴会发生“下凹”现象,轴箱外置车辆的车轴会发生“上凸”现象。随轴重增加,2种车型的车轮偏角都会增大,当轴重为12 t时,轴箱内置车辆的车轮偏角为0.067°,轴箱外置车辆车轮偏角为−0.093°。
2)轮轴弯曲会造成轮对内侧距、接触点位置发生变化。当轴重为6 t 时,轴箱内置车辆的轮对轴心线下方内侧距增大0.40 mm,轴箱外置车辆的轮对轴心线下方内侧距减小0.57 mm;当轴重为12 t时,轴箱内置车辆的轮对轴心线下方内侧距增大0.81 mm,轴箱外置车辆的轮对轴心线下方内侧距减小1.14 mm。当轮对横移量为[0,6]mm和(9,12]mm时,2种车型在钢轨上接触点位置基本保持一致;当轮对横移量为[6,9]mm 时,2 种车型接触点位置变化相对明显,轴重为12 t;当轮对横移量为6 mm 时,2 种车型在钢轨上的接触点位置相差6.09 mm,轴箱内置车辆的接触点更偏向于轨距角侧。
3)从轮轨静态匹配看出,横移量在[0,3]mm时,轴箱内、外置车辆的等效锥度基本相等;横移量在[4,12]mm 时,轴箱内置车辆的等效锥度比轴箱外置车辆的等效锥度大。因此,从接触特性上轴箱内置车辆也体现了更好的曲线通过性能。
4)当轮对横移量在[0,6]mm 内时,轴箱内、外置车辆轮轨接触斑基本呈现椭圆形状;2种车型的轮轨接触应力最大值、轮轨Von-Mises等效应力基本保持一致。

