考虑时变效应的堆载引发邻近单桩水平变形分析

闵鹏，申玉生，林作忠，董俊，雷龙

(1.西南交通大学交通隧道工程教育部重点实验室，四川成都，610031；2.中铁第四勘察设计院集团有限公司，湖北武汉，430063)

随着城镇化进程的发展，城市建设用地日益紧张。桩基被广泛应用于高层建筑、桥梁墩台、港口码头等基础工程中。近年来，由邻近地面堆载引发的工程事故屡见不鲜[1−3]。地面堆载将改变地层原有的应力状态，导致既有桩基挠曲变形，进而引发一系列不利影响。因此，准确地预测地面堆载对邻近既有桩基产生的变形具有重要的现实意义。目前，各国学者对此类似问题进行了广泛研究，主要包括理论解析、数值模拟、现场监测和模型试验等。

与数值模拟、现场监测和模型试验相比，理论解析作为一种低成本而高效率的分析方法，适用于指导工程的初步设计。在目前的理论研究中，通常采用两阶段法来分析地面堆载对桩基的影响[4−6]。基于两阶段法，许多研究者从地基弹性入手，将桩基简化为搁置在Winkler弹性地基上的连续梁[7−9]。Winkler模型将地基看作由若干互不影响的独立弹簧组成，地基表面任一点处反力仅与该点弹簧的变形量成正比，该模型简化了地基复杂的力学现象，但忽略了弹簧间的剪切作用和地基的连续性，不能很好地反映土体的力学特性。为了克服这一缺陷，梁发云等[10−11]采用Pasternak 双参数地基模型来模拟桩−土间的相互作用，将桩基简化为Euler-Bernoulli 梁，建立了桩身的挠曲控制微分方程。Pasternak 双参数地基模型在Winkler 模型的基础上假定地基弹簧之间存在剪切效应，在各弹簧顶部增加一层剪切层，从理论上改进了Winkler 地基不连续的缺陷。此外，大多研究将桩基简化为Euler-Bernoulli 梁，仅考虑了弯曲变形而忽略了剪切效应的影响，导致桩基的剪切刚度被高估，不能很好地反映桩基的实际受力状态。而Timoshenko 梁理论适用于大多数桩基，并能得到更加精确的结果[12]。目前已有究者采用Timoshenko 梁来模拟桩基[13−16]，同时考虑了桩基的弯曲效应与剪切效应。

上述的理论研究中很少考虑时间对桩−土间相互作用的影响。然而，实际工程中桩基的变形会随着时间的变化逐渐发展，在长期的变形过程中应考虑土体的流变性对桩基的影响[16]。采用简化黏弹性模型和弹性−黏弹性对应原理来研究土体流变性问题是目前较为普遍的研究方法[17]。张强[18]基于黏弹性地基梁理论，建立了开挖卸荷导致下方既有隧道发生隆起位移的竖向变形公式，分析了时间对变形的影响。张治国等[19−20]基于Boltzmann黏弹性模型，采用两阶段法研究了黏弹性地基中基坑开挖对邻近桩基水平位移的影响及其随时间的变化趋势。但在地面堆载引发邻近既有单桩水平变形的研究中大多未考虑时间的影响。

因此，本文作者从地基黏弹性角度出发，基于两阶段法，提出一种预测黏弹性地基中地面堆载引发邻近既有单桩水平变形的简化分析方法，并通过有限差分和Laplace 逆变换求得单桩水平变形黏弹性解。将本文所得理论解与数值模拟结果进行比较，并与已有解进行对比分析，验证本文方法的正确性。最后，分析Burgers 模型参数、竖向均布堆载、水平均布堆载以及堆载−桩体水平距离对既有单桩水平变形的影响。

1 桩体附加应力黏弹性解

1.1 黏弹性半空间Boussinesq解

Boussinesq解为半无限体表面一点受法向集中力作用的经典弹性解[21]，可以用于研究地面荷载作用下在岩土体内部产生的附加应力场问题。计算模型如图1所示。

图1 半无限体表面受集中力示意图Fig.1 Schematic diagram of half space with forces applied on surface

在半无限体表面O(0，0，0)处竖向集中荷载F作用下，半无限体内一点H(x，y，z)处引起的水平附加应力σx(x，y，z)为

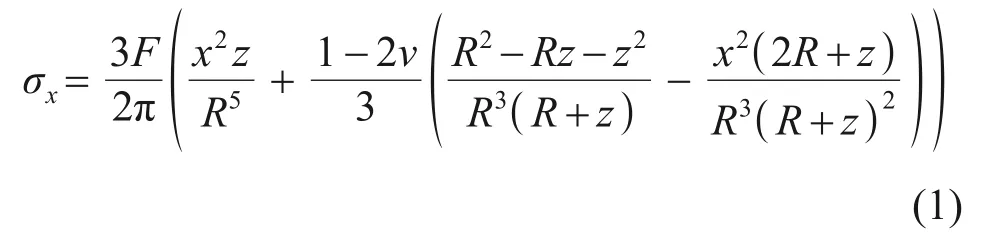
式中：ν为泊松比；R为H点到O点的距离，R=

Burgers 模型是一种常用的线性黏弹性模型，可以较好地反映土体的流变性，既能描述加载初期的瞬时弹性变形，又能描述土体随时间变化的特性[22−24]。本文选用Burgers 模型模拟岩土体的黏弹性本构关系，研究黏弹性半空间体表面堆载在空间内部某一点所产生附加应力的拟静态黏弹性解。所采用的Burgers 模型由一个Maxwell 单元和一个Kelvin单元串联组成，如图2所示。

图2 Burgers模型示意图Fig.2 Schematic diagram of Burgers model

根据Burgers 黏弹性模型，在一维条件下岩土体的本构关系可以表示为

对于各向同性黏弹性材料，在三维应力状态下，可将应力、应变张量分别分解为球张量与偏张量，应变球张量只与应力球张量有关，应变偏张量只与应力偏张量有关。因此，三维黏弹性体本构关系一般为：

式中：Sij为应力偏张量；eij为应变偏张量；σ为应力球张量；e为应变球张量；P′，Q′，P″和Q″为黏弹性本构方程的微分算子，

空间三维应力状态下，Burgers 黏弹性模型中反映岩土体弹性和黏性的本构关系分别为：

式中：G为剪切模量；η为黏滞系数。

将岩土体的本构关系分为剪切变形和体积变化2 部分，其中，剪切变形服从Burgers 黏弹性本构关系，则其偏张量部分的表达式为

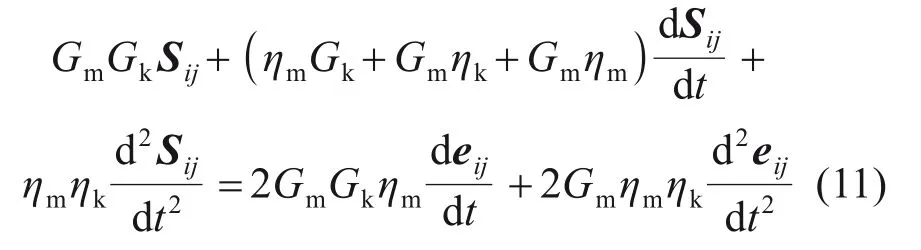
体积变化服从弹性本构关系，则其球张量部分的表达式为

式中：K为体积模量。

将式(11)和(12)代入式(5)～(8)可得黏弹性本构关系各微分算子分别为：

对式(13)～(16)进行Laplace变换可得：

黏弹性材料参数的Laplace 变换与各微分算子间的关系为：

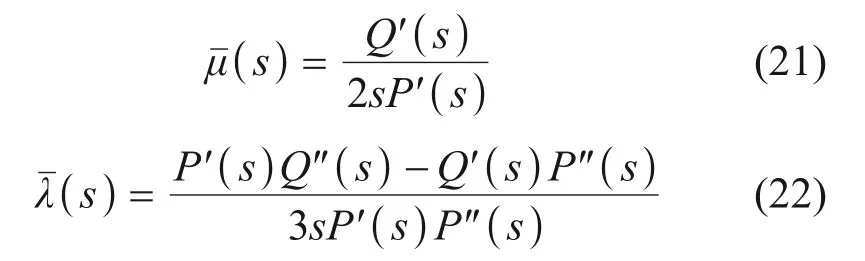
由弹性力学关系可得：

式中：ν为泊松比；μ和λ为拉梅系数。

根据弹性−黏弹性对应原理，将(s)和(s)代替式(23)和(24)中的μ和λ，即可得到黏弹性条件下泊松比ν(s)的Lapalce变换式分别为：

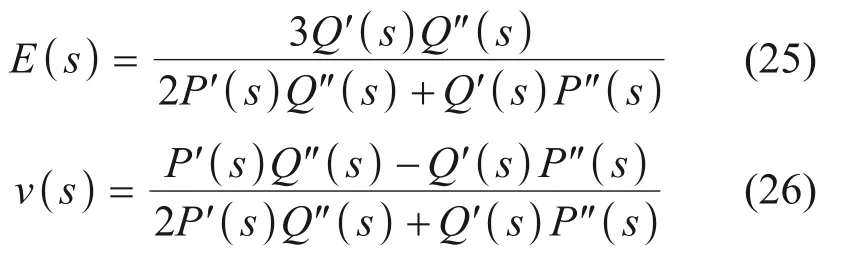
将式(17)～(20)代入式(25)和(26)可得：

假定半无限黏弹性体表面原点O处的法向集中荷载F(t)=FH(t)，并对F(t)进行Laplace 变换可得：

根据弹性−黏弹性对应原理，将式(26)代入式(1)，即可得到在表面集中荷载F作用下半无限体内部任意一点H(x，y，z)处x向水平附加应力关于时间t的Laplace变换：

其中，

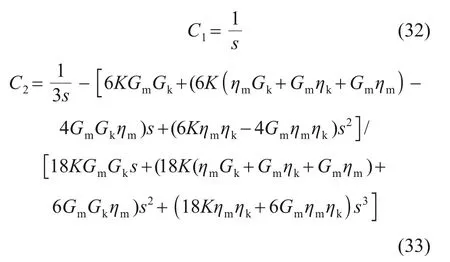
对式(31)～(33)进行Laplace 逆变换，可得到集中荷载F作用下基于Burgers 模型的水平附加应力在时间域上的黏弹性解：

其中，

1.2 桩体水平附加应力黏弹性解

以荷载中心为坐标原点建立如图3所示的附加应力计算模型，图中，H为桩长，B和L分别为堆载宽度和堆载长度，在B×L内作用法向均布荷载F。

图3 单桩计算模型示意图Fig.3 Schematic diagram of computing model of pile

根据式(34)，由荷载微元Fdxdy在桩体任意深度M(L0，Y0，z)处所产生的水平附加应力为

在B×L内对式(36)进行积分，即可求出地面均布荷载F引起桩体轴线上任意一点P(L0，Y0，z)处水平附加应力为

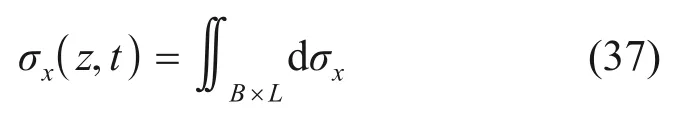
引入数值积分进行求解式(36)，为了使结果能够达到较高的代数精度，还需对积分式进行复化处理，对荷载积分区间进行等分，要求每个矩形子区间边长不超过1 m，对各子区间运用Gauss-Legendre数值积分公式求解，将各子区间积分值叠加即可得到桩体水平附加应力σx(z,t)。

2 桩体水平变形黏弹性解

通过两阶段分析法研究地面堆载作用下单桩水平挠曲黏弹性解。第一阶段，忽略桩体的存在，考虑土体的流变性并结合传统的Boussinesq解推导出地面堆载引发的土体附加应力黏弹性解；第二阶段，将地面堆载引发的附加应力作为外荷载施加在桩体上，根据黏弹性地基梁理论，并结合有限差分法求得单桩水平挠曲的理论解。

2.1 桩−土系统计算模型

在Pasternak 地基模型的基础上，引入能够考虑土体流变性的线性黏弹性地基模型，如图4所示。该模型由若干个Burgers 线性黏弹性单元体和能反映单元体间剪切相互作用的剪切层组成，其表达式为

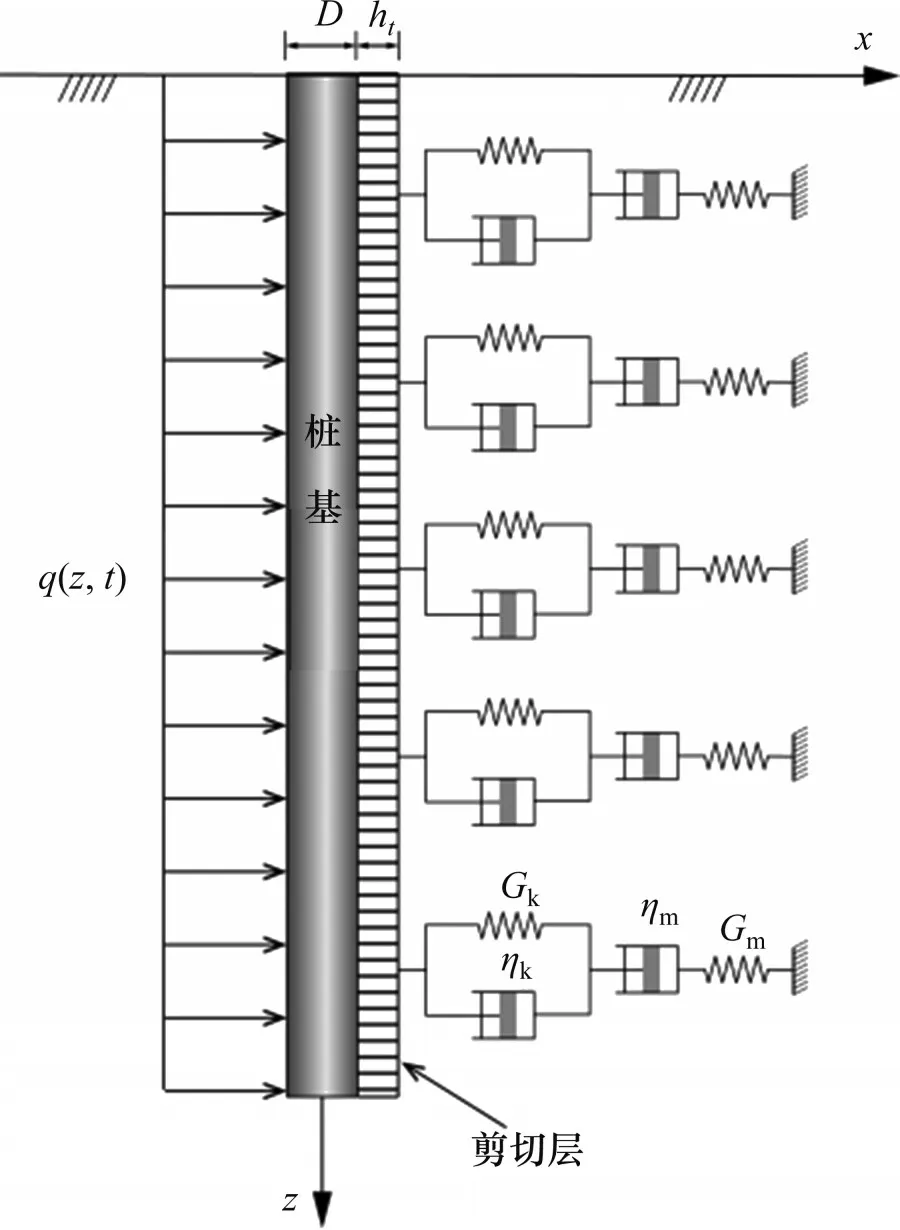
图4 黏弹性地基模型示意图Fig.4 Schematic diagram of viscoelastic foundation model

其中：

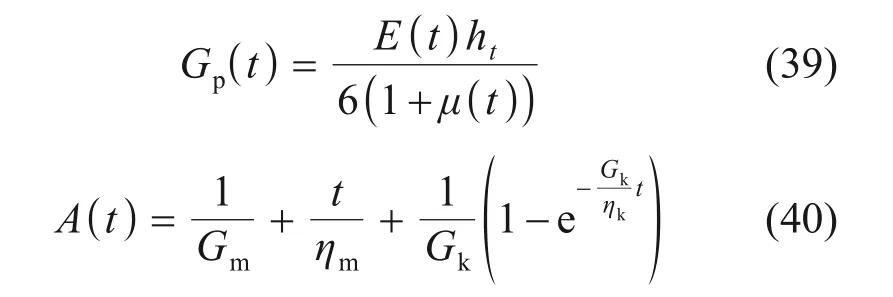
p(z,t)为地基反力；ω(z,t)为桩体的水平位移；Gp(t)为剪切层刚度；A(t)为蠕变柔量；E(t)和μ(t)分别为考虑时变效应的地基弹性模量和地基泊松比；ht为Pasternak 剪切层厚度，本文取ht=11D[19]，D为桩体等效宽度。

为简化计算，对该模型进行如下基本假定：1)桩体为考虑剪切效应的Timoshenko 矩形梁，其等效剪切刚度为κGA0，等效抗弯刚度为EI，等效宽度为D；2)桩体与周围土体接触紧密，不考虑桩−土间相对滑动及摩擦力；3)假设地基连续均匀，不考虑土体的成层性；4)Pasternak 剪切层不可压缩，仅产生剪切变形；5)不考虑重力产生的影响。

取桩体上一微元段进行受力分析，如图5所示。根据材料力学，微元段水平受力平衡方程和弯矩平衡方程分别为：

图5 微单元受力分析Fig.5 Viscoelastic foundation model

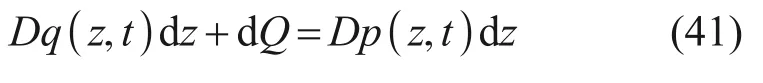
式中：q(z,t) 为作用在桩体上的附加荷载，由式(37)计算；Q为剪切力；p(z,t) 为黏弹性地基反力；M为弯矩。

由Timoshenko 梁理论，桩体剪力Q与弯矩M表达式为：

式中：κ为截面系数，此处取κ=0.83；G为桩体剪切模量，G=E/2(1+μ0)，μ0为桩体泊松比；A0为桩体横截面积；θ为转角。

根据式(41)～(44)可推导得地面堆载作用下，桩体水平位移ω(z,t)、桩体弯矩M(z,t)和剪力Q(z,t)的控制微分方程分别为：

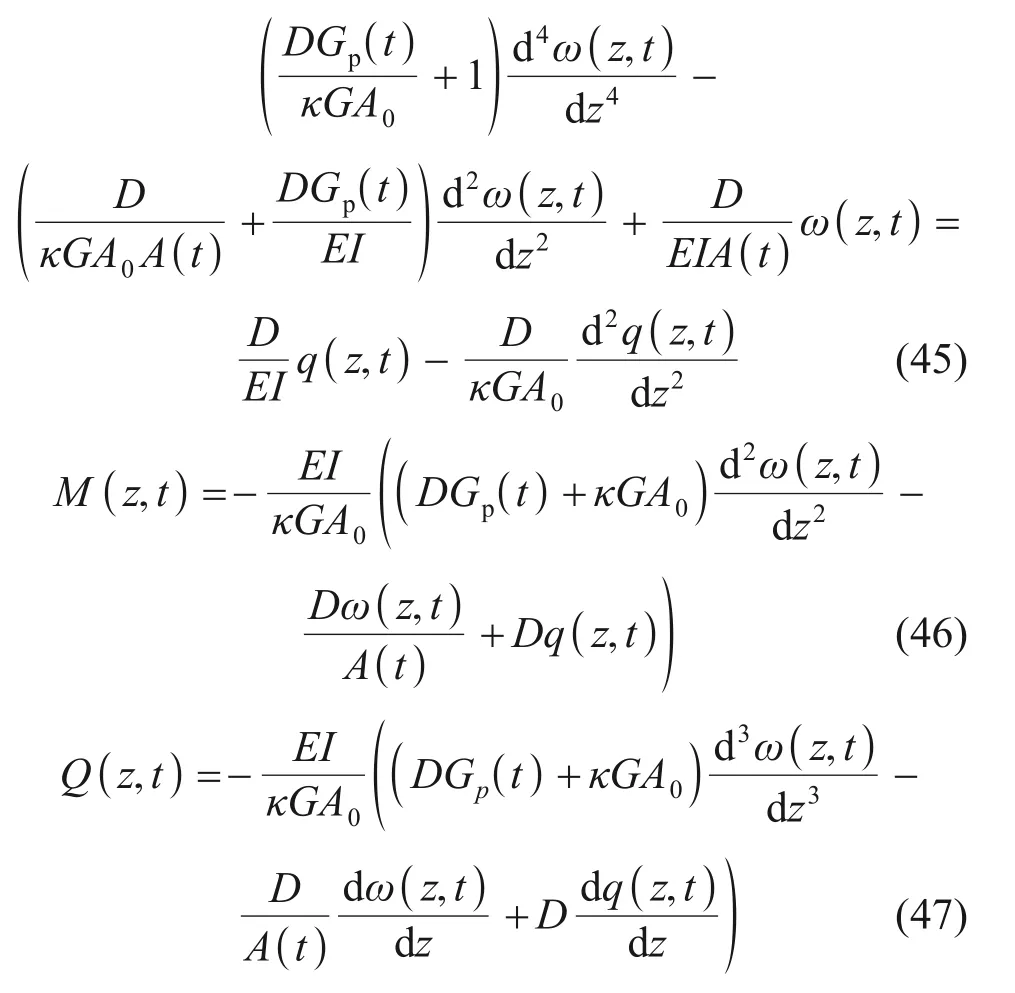
2.2 桩体水平变形求解

对式(45)进行关于时间t的Laplace变换可得：

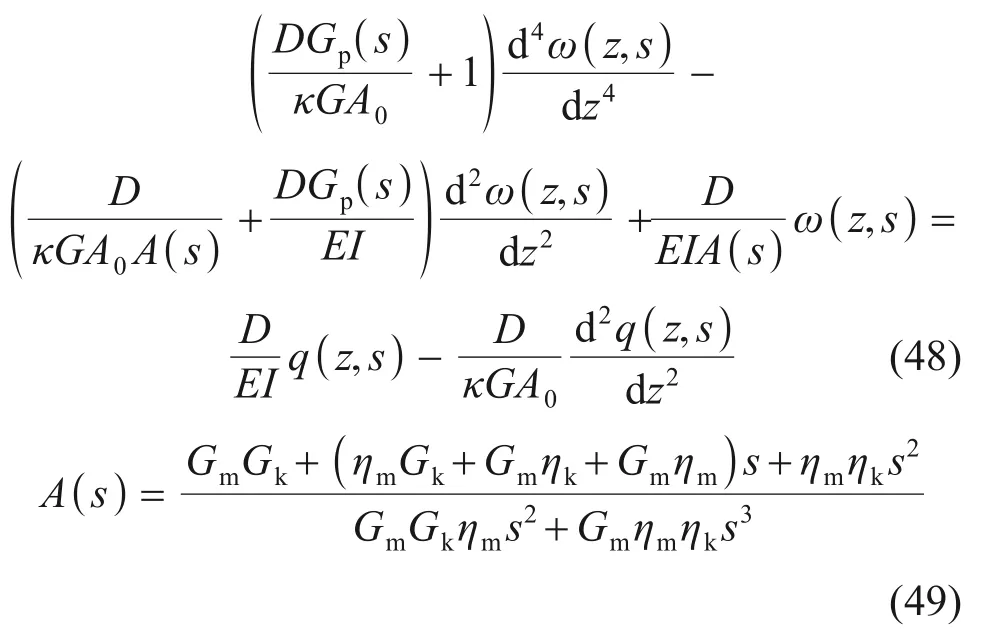
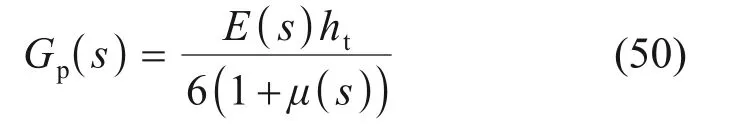
式中：ω(z,s)和q(z,s)分别为ω(z,t)和q(z,t)的Laplace 变换；A(s)和Gp(s)分别为A(t)和Gp(t)的Laplace 变换；E(s)和μ(s)分别为地基弹性模量和地基泊松比的Laplace变换。

对式(48)采用有限差分法进行数值求解。桩体有限差分示意图如图6所示，将桩体划分为n个长度相同的微元段，并在桩体顶部和底部分别增设2个虚拟节点用以计算桩体的边界条件。

图6 桩体有限差分示意图Fig.6 Schematic diagram of finite difference of pile

根据有限差分原理，式(48)的差分形式为

式中：l为单元长度，l=H/n，H为桩长；下标i为节点编号，i∈(0，n)。

考虑桩体两端自由无约束时，桩体顶部和底部弯矩和剪力均为0。结合有限差分原理，桩体弯矩和剪力分别为：

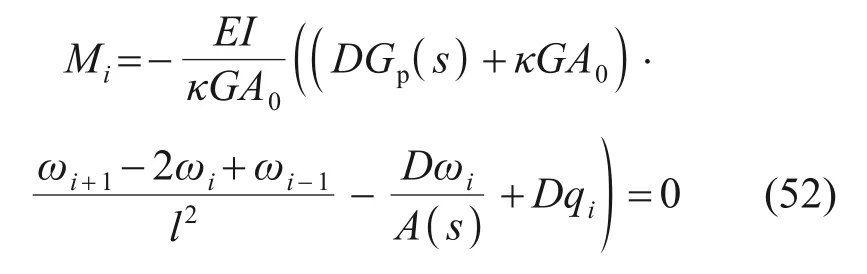
式中，当下标i=0 时，表示桩体顶部处弯矩和剪力；当下标i=n时，表示桩体底部处弯矩和剪力。

根据式(52)～(53)可以得到桩体两端虚拟节点位移为：

将虚拟节点位移式(54)～(57)代入式(51)，可将差分方程改写为向量和矩阵表达式：

根据式(58)即可解得在地面荷载作用下桩体的水平变形ω(z,t)，并对ω(z,t)进行Laplace 逆变换即可得到桩体在时间域上的水平变形黏弹性解ω(z,t)：

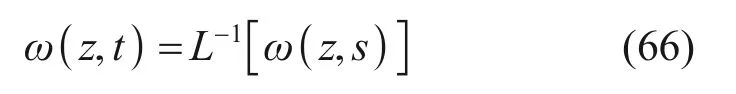
特别地，当桩体等效剪切刚度κGA0取无穷大时，ω(z,t) 将退化为欧拉梁上的解，当t取0 时，退化为Pasternak地基上的弹性解。

3 分析与验证

3.1 收敛性研究

桩单元划分数量是本文求解的关键，微元段划分精度直接决定最终求解的精度，因此在上述公式的基础上，编制专门的Matlab 计算程序，通过收敛性分析，得到微元段划分的最优个数。收敛性判断标准如下：

式中：k为当前迭代次数；k-1为前一次迭代次数；c为容许误差，此处取为0.1 mm。

假设地面堆载范围B×L=30 m×50 m，堆载载荷F=150 kN/m2。荷载中心距离桩体中线20 m。桩体等效宽度为1.0 m，桩长为40 m，桩体弹性模量为31.5 GPa，泊松比为0.2。Burgers 模型参数可根据实际工程的监测数据进行参数反演或对室内蠕变试验曲线进行拟合来确定[25−26]，本文地基体积模量K=0.68 GPa，Kelvin 黏滞系数ηk=0.1 GPa·d，Kelvin 弹性模量Gk=3.0 MPa，Maxwell 黏滞系数ηm=75.0 GPa∙d，Maxwell 弹性模量Gm=5.0 MPa。图7所示为深度z=20 m 处桩体水平位移与微单元划分数量的关系曲线。从图7可以看出，当微元段数量达到40，桩体中点水平位移稳定收敛，位移变化可以忽略不计，因此，在同时考虑其他因素的条件下，桩体微单元长度不超过1 m即能满足计算收敛。

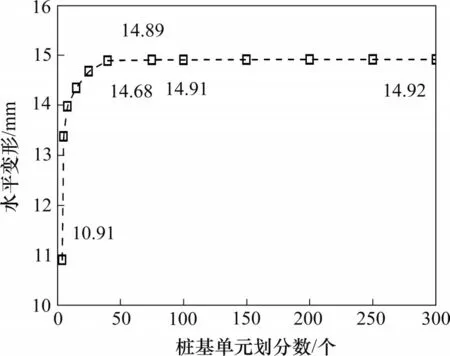
图7 水平变形随单元划分数的变化Fig.7 Variation of deformation with number of element

3.2 数值验证

为了验证所提理论解的正确性，采用FLAC3D有限差分软件建立三维数值模型模拟地面堆载作用下邻近单桩的水平挠曲，通过对比数值模拟与理论解的计算结果验证本文分析方法的正确性。三维数值模型如图8所示。为了提高数值计算的精度，对桩体及其周围网格进行了细化处理，模型x×y×z=150 m×120 m×60 m，其余计算参数同3.1节。

图8 数值计算模型Fig.8 Numerical model

图9所示为深度z为5.0，15.0，25.0 和35.0 m处桩体的水平变形曲线。从图9可以看出，地面堆载作用下桩体的水平变形有明显的时变效应。在t=0 d时，深度z为5.0，15.0，25.0和35.0 m处，本文方法计算的水平变形分别为7.17，6.98，3.87 和1.87 mm；t=500 d时，相应位置的水平变形分别为19.98，18.05，11.45 和5.42 mm，随时间的延长，相应位置的变形分别为12.81，11.07，7.58 和3.55 mm，依次占总水平变形的64.1%，61.3%，66.2%和68.3%。在t=0 d 时，由于地基的弹性效应，加载瞬间桩体产生变形，在t=0～120 d 时，桩体变形速率持续减小，但此阶段桩体水平变形随时间不断累积，土体流变性的影响最为显著，120 d 后，进入稳定变形阶段，桩体的水平变形速率不再发生变化，变形趋于平稳。因此，地面堆载施加后的120 d内是对桩体水平变形影响最大的时间段。对比本文解与有限差分数值解可以看出，本文解与有限差分数值解有较好的一致性，说明本文推导的地面堆载引发邻近单桩水平变形的黏弹性解具有较高的计算精度。

图9 桩体水平变形−时间关系曲线Fig.9 Curves of pile horizontal deformation and time

3.3 案例验证

与冯昌明等[6,27]提出的堆载引发桩体水平变形计算方法进行对比分析，其中案例基本工况如下：地面矩形均布堆载范围长×宽为6 m×6 m、载荷为20 kPa，桩体轴线与堆载边缘净距为2 m，桩长为21 m，桩径为0.5 m，桩体和土的弹性模量分别为40 GPa 和5 MPa，泊松比为0.3[27]。计算结果如图10所示，从图10可以看出：本文方法所得桩体水平变形与文献[6,27]所得结果基本吻合，从而验证了本文方法的正确性。

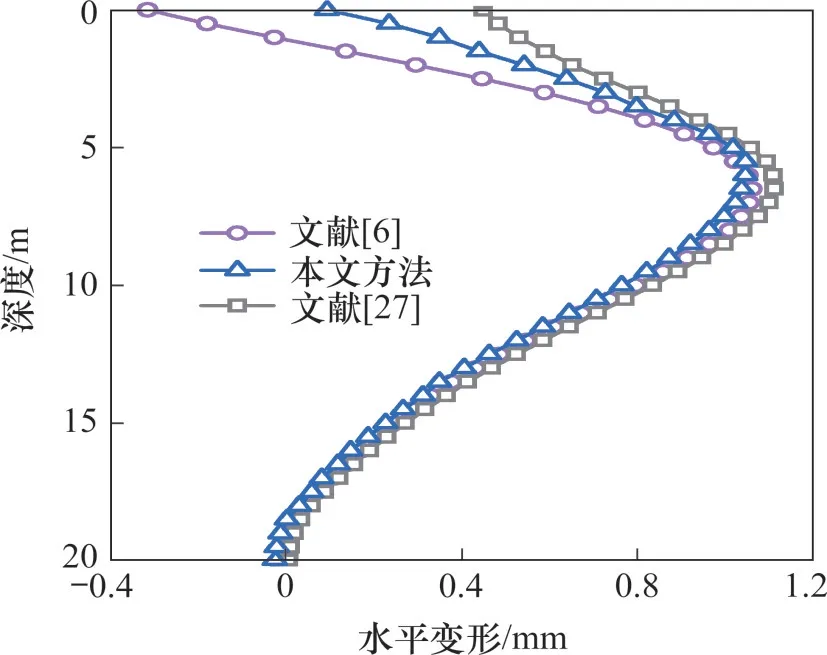
图10 桩体水平变形曲线Fig.10 Horizontal displacement of pile

4 Burgers模型参数分析

4.1 Maxwell弹性模量的影响

在其他参数不变的情况下，取Maxwell弹性模量Gm分别为2.5，5.0 和7.5 MPa，探究Gm对地面堆载作用下桩体水平挠曲的影响。图11所示为t=0 d 和t=120 d 时不同Gm下桩体的水平变形。从图11可以看出：Gm对桩体水平变形的影响显著，Gm越小，桩体水平变形越大，桩体水平变形对Gm的变化越敏感。对比不同时刻桩体水平变形曲线还可以看出：当t=120 d 时，水平变形量显著增加，说明桩体水平变形有明显的时变效应。

图11 不同Gm下桩体水平变形对比Fig.11 Horizontal deformation comparison of pile with different Gm

4.2 Kelvin弹性模量的影响

在其他参数不变的情况下，取Kelvin 弹性模量Gk，分别为1.5，3.0和4.5 MPa，探究Gk对地面堆载作用下桩体水平挠曲的影响。图12所示为t=0 d 和t=120 d 时不同Gk下桩体的水平变形曲线。从图12可以看出，t=0 d时，不同Gk下桩体的水平变形几乎一致，说明堆载施加瞬间桩体的水平变形不受Gk的影响。在t=120 d时，桩体的水平变形与t=0 d 时相比有明显增加，说明土体的流变性对桩体水平变形有显著影响，同时，t=120 d 时，Gk越小，桩体的水平变形越大，说明在Burgers 体中瞬时变形主要受Gm的影响而与Gk无关，Gk主要反映由时变效应产生的黏弹性变形。

图12 不同Gk下桩体水平变形对比Fig.12 Horizontal deformation comparison of pile with different Gk

4.3 Maxwell黏滞系数的影响

在其他参数不变的情况下，取Maxwell黏滞系数ηm分别为15.0，30.0和75.0 GPa·d，探究ηm对地面堆载作用下桩体水平挠曲的影响。图13所示为不同ηm下深度20.0 m 处桩体水平变形曲线。从图13可以看出，在t=0～120 d时，不同ηm下桩体水平变形对于时间的响应规律基本一致，说明在此时间段桩体水平变形几乎不受ηm变化的影响。当t>120 d 后，桩体进入稳定变形阶段。ηm越小，桩体水平变形速率越快，导致桩体随时间发展累积更大的水平变形，说明ηm对最终桩体水平变形值有直接影响。

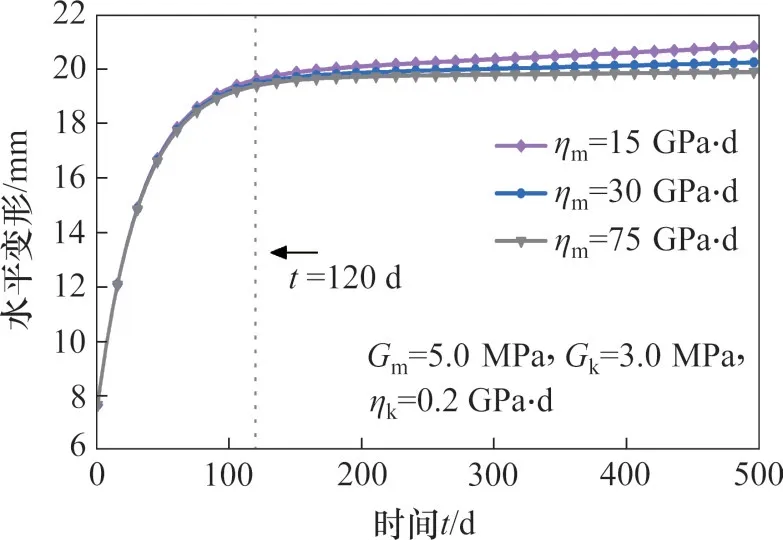
图13 不同ηm下桩体水平变形−时间关系曲线Fig.13 Curves of horizontal deformation and time of pile with different ηm

4.4 Kelvin黏滞系数的影响

在其他参数不变的情况下，取Kelvin 黏滞系数ηk分别为0.1，0.2和0.4 GPa·d，探究其对地面堆载作用下桩体水平挠曲的影响。图14所示为不同ηk下深度20.0 m 处桩体水平变形曲线。从图14可以看出，ηk对桩体瞬时变形几乎没有影响，对桩体最终水平位移也无明显影响，但是对于流变变形进入稳定变形阶段的时间有明显影响。ηk越大，进入稳定变形阶段的时间越长，当ηk=0.1 GPa·d时，桩体水平变形在t=70 d后基本稳定，而当ηk=0.4 GPa·d时，桩体水平变形在t=240 d 后才基本稳定，历时明显增加。因此，在实际工程中应根据ηk的实际取值制定监测方案。

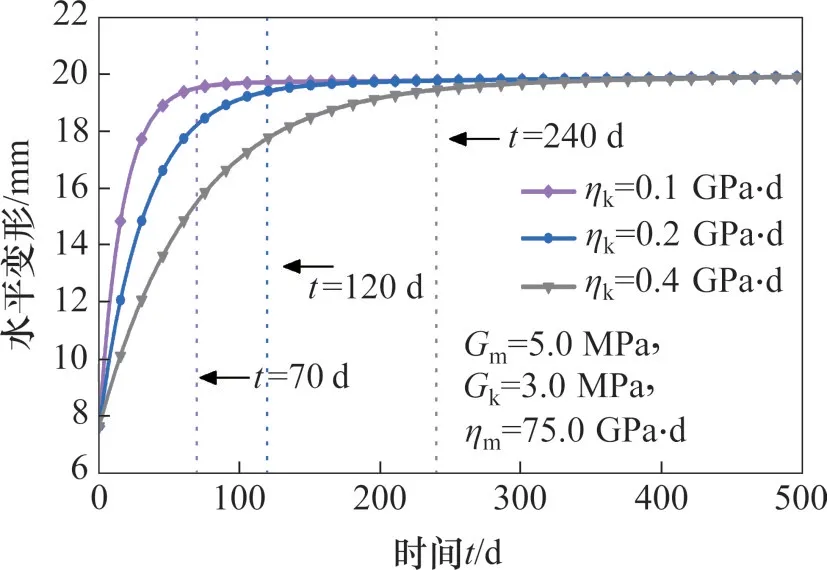
图14 不同ηk下桩体水平变形−时间关系曲线Fig.14 Curves of horizontal deformation and time of pile with different ηk

5 堆载影响分析

5.1 堆载宽度的影响

在其他参数不变的情况下，取堆载宽度B分别为20.0，50.0 和100.0 m，探究在黏弹性条件下B对桩体水平变形的影响。图15所示为t=0 d 和t=120 d 时，不同堆载宽度下桩体的水平变形。从图15可以看出，B对桩体水平变形有明显的影响，B越大，桩体水平变形越大，同时桩体水平变形对B的变化也越敏感。对比t=0 d和t=70 d时桩体水平变形曲线，不难发现桩体水平变形随着时间的发展逐渐累积，地基的流变性对桩体水平变形有明显影响。

图15 不同B时桩体水平变形对比Fig.15 Horizontal deformation comparison of pile of with different B

图16所示为B为20.0 m和100.0 m，t=120 d时桩体周围土体的水平应力分布。从图16可以看出：随着堆载宽度增加，土体水平应力明显增加，桩体产生更大的水平变形。

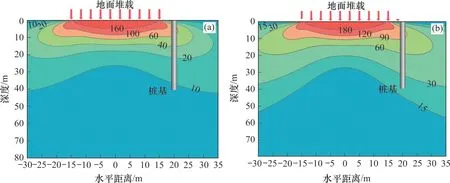
图16 不同B时土体的水平应力分布Fig.16 Horizontal stress distribution of soil with different B

5.2 堆载载荷的影响

在其他参数不变的情况下，取均布载荷F分别为100.0，150.0 和200.0 kN/m2，探究在黏弹性条件下F对桩体水平变形的影响。图17所示为t=0 d和t=120 d 时不同F下桩体的水平变形。从图17可以看出，随着F增加，桩体产生更大的水平变形，说明F对桩体变形有显著影响。

图17 不同F时桩体水平变形对比Fig.17 Horizontal deformation comparison of pile with different F

F分别为100.0 kN/m2和200.0 kN/m2，t=120 d时桩体周围土体的水平应力分布如图18所示。从图18可以看出：随着F增加，土体水平应力明显增加，导致桩体处水平附加应力增加，桩体产生更大的水平变形。

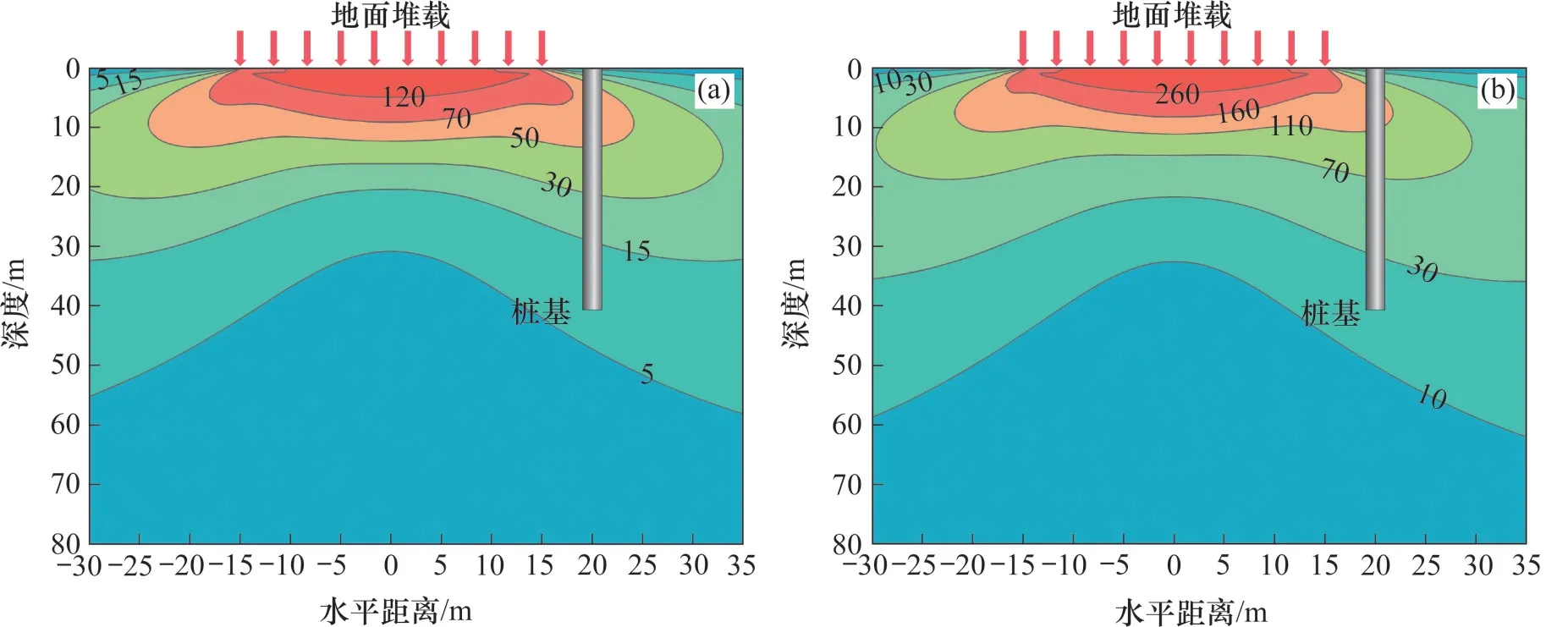
图18 不同F时土体水平应力分布Fig.18 Horizontal stress distribution of soil with different F

5.3 堆载−桩体水平距离的影响

在其他参数不变的情况下，取堆载−桩体水平距离L0分别为20，25 和30 m，探究其对地面堆载作用下桩体水平变形的影响。图19所示为t=0 d和t=120 d时不同L0下桩体的水平变形。从图19可以看出，在深度0～25 m 范围内，L0越小桩体水平变形越大，在深度大于25 m 时，桩体水平变形基本不受L0影响。对比t=0 d和t=120 d时桩体的水平位移还可以看出：桩体的水平变形有明显的时变效应。

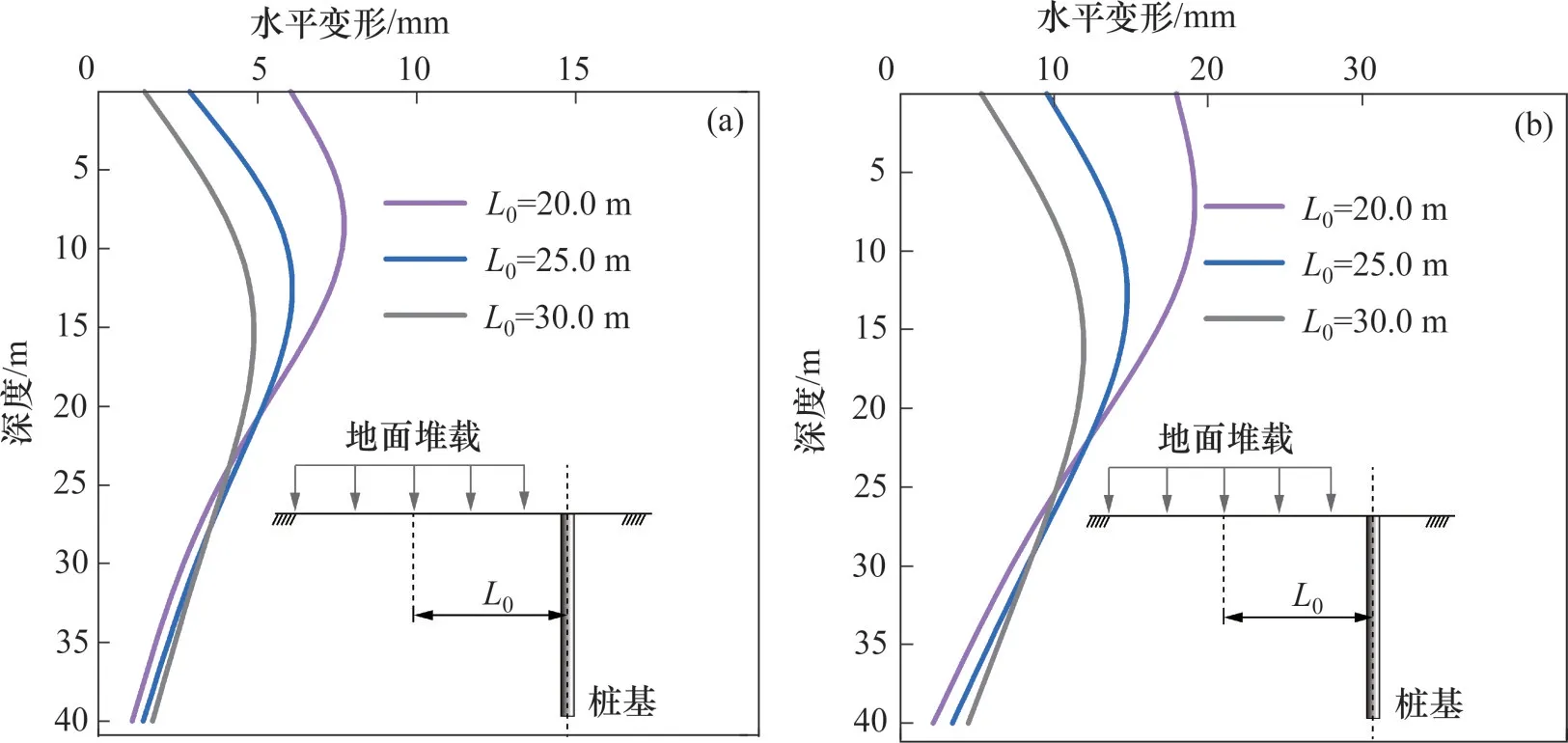
图19 不同L0时桩体水平变形对比Fig.19 Horizontal deformation comparison of pile with different L0

6 结论

1)微元段划分数量直接影响黏弹性解的求解精度，当微元段划分数量达到40，桩体水平变形即可稳定收敛。

2)黏弹性地基上桩体水平变形有明显的时变效应，与数值模拟结果有较好的一致性，验证了本文方法预测地面堆载作用下桩体水平变形的准确性，通过与已有解进行对比分析，进一步验证了本文方法的正确性。

3)Burgers 模型各参数对桩体水平变形均有较大影响。Gm对桩体瞬时变形有较大影响，Gk主要反映由时变效应产生的黏弹性变形，ηk决定变形进入稳定阶段的时间跨度而对最终变形量基本没有影响，ηm主要影响桩体稳定变形阶段的变形速度。

4)地面堆载宽度和堆载载荷对桩体水平变形均有较大影响，并且桩体水平变形随着堆载中心与桩体水平距离的减小而明显增加。

5)本文主要研究均质地基中黏弹性条件下堆载引发邻近既有实心单桩的水平变形响应，并未考虑地基土的成层性、开口管桩和群桩基础等工况，因此，本文方法不能分析地基成层性、开口管桩土塞效应和群桩效应等对桩体水平变形的影响，针对这些问题，还需要进一步研究。