基于单视几何的身高测量算法的设计与实现

李杰,王婷，邢笑笑

(商洛学院，陕西商洛 726000)

人体的几何特征是判断和识别任务信息的一项重要参数，在很多领域都有所应用[1]。例如：在刑事侦查方面，利用拍摄到的嫌疑犯的背影图像来确定目标任务的身高信息，可以缩小搜查范围以提升破案效率；在智能交通领域里，利用图像测量技术可以快速地检测出身高条件符合优惠政策的小孩，提高乘车效率，减少乘车拥堵现象的发生；在智慧医疗领域，利用图像检测技术快速检测出人们的身高，大大提高了体检效率。由于人们对工作效率的需求，使得基于图像的身高测量算法有了重要的研究意义和应用前景。

近年来，由于数字图像处理技术的广泛应用，基于图像的身高测量算法的研究引起了研究人员极大的兴趣。

在有关图像测量的基础方面，19 世纪70 年代初期人们采用图像相机标定[2]的研究方法，在图像物体测量的多个角度研究图像和实际环境中物体的相互对应关系，并初步建立起了基于相机校准的线性变换模型，该线性模型的参数可以通过求解线性方程组来得到。

董秋雷等[3]提出了在高度校准应用场景中实时测量人体高度的算法。甘志杰等[4]提出了利用大津自适应阈值分割的算法和高速连接区域标记的算法,通过事先获取的人体位置坐标初步测量身高信息,然后根据相机上的成像模型对测量结果进行修正,获得了相对准确的身高信息。张烨等[5]提出一种单目视频未标定状态下的人体运动测量系统设计方案，该方案采用极大似然估计算法求解场景中的消失点和消失线，根据射影变换的交比不变量确定人体实时身高。方强[6]将Grabcut图像分割算法运用到婴儿的身高测量中，取得了较好的测量效果。本文将单视几何的测量算法应用到身高测量中，这种身高测量算法与传统的身高测量方法相比不需要其他复杂的仪器，仅用一张图片即可完成对身高的测量，节省了测量成本，并能在一定程度上降低测量误差。

1 相关技术

1.1 平面场景的相机标定

平面场景的相机标定是基于单视几何图像测量的关键技术，其目的在于寻找单视世界空间坐标系和单视像素坐标系之间的映射关系，称之为投影矩阵。如果求出了单视几何中世界空间坐标系和像素坐标系之间的映射关系，就可以根据图像的像素坐标推导出映射点的世界坐标。相机标定一般利用直接线性变换法[7]来确定映射关系的参数，根据相机周边图像与相机物体的运动关系，确定基于相机周边图像的立体几何直接线性变换模型，并通过直接求解线性方程组来准确估计线性变换模型的具体参数。

利用直接线性变换对相机进行标定时是将像点和物点的成像几何关系在齐次坐标系下写成透视投影矩阵的形式如公式(1)所示：

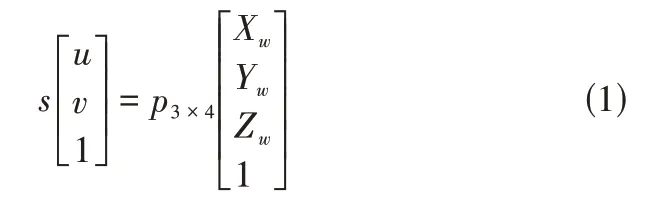
公式(1)中(u,v,1)图像坐标系下点的齐次坐标，(Xw,Yw,Zw)为世界坐标系下空间点的欧式坐标，P为3*4的透视投影矩阵[8]，S为未知尺度因子。由于物点在测量平面内，故可让世界坐标系下Zw=0，消去S并将公式(1)展开可得到公式(2)：

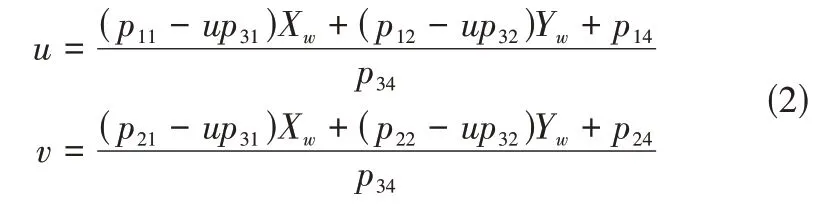
令：

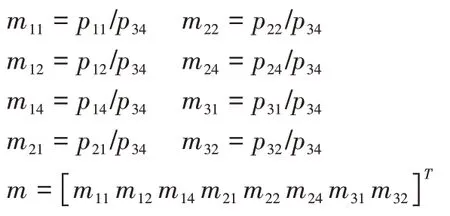
可用矩阵将公式(2)表示为公式(3)所示：

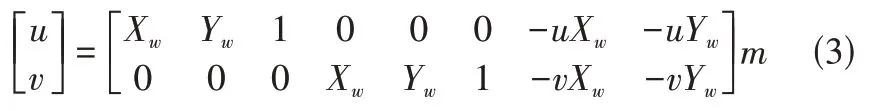
由公式(3)可知，只要求出m就可以求出相机的内外部参数，从而知道图像坐标系与世界坐标系之间的转换关系。

1.2 最小二乘法

最小二乘法[9]也简称最小平均式方法，是一种数学优化技术，它通过数学方法计算最小化误差的平方和寻找函数的最佳函数匹配，可以求得未知的数据，使得求得的已知数据和实际数据之间误差的平方和达到最小。

以孤石B为研究对象对其进行力学分析，孤石受到重力G作用，支持力N及其他外部作用力F1、F2等。假定孤石B在下部支撑孤石A接触面的倾角为θ，βi为外部作用力与水平方向夹角，孤石倾倒时绕支点O进行，O点到重力作用线的距离为x，di为O点到F作用力的力臂。本文分析中皆以接触面方向为X轴，接触面法线方向为Y轴，则孤石B的力学平衡方程为：

两个变量(x,y)之间的关系通常可以得到几对数据(x1,y1)、(x2,y2)……(xm,ym)，其中m为样本容量，即实验次数，xi,yi分别表示任意一组实验x和y的数值。将这些数据绘制在X-Y直角坐标系中，如果这些点靠近直线，则选择用直线表示，如公式(4)所示：

其中：a0、a1是任意实数。

令：

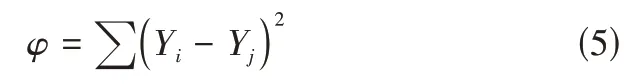
将公式(4)代入公式(5)中可得：

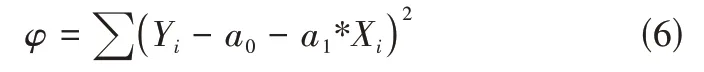
当 ∑(Yi-Yj)平方最小时，可用函数φ对a0、a1求偏导数，令这两个偏导数等于零，可得到两个关于a0、a1为未知数的两个方程组，将求解出来的a0和a1带到公式(4)中，此时的Yj=a0+a1X就是回归求得的一元线性方程，即数学模型。

在回归过程中，对于所有回归集合包括任何数据点(x1,y1)、(x2,y2)……(xm,ym)不可能在回归的方程中。为了评估相关性，可以使用相关系数R、统计系数F、残差标准偏差S 来判断。R 越接近1，其相关性就越高，|R| 越大越好，S 越接近0越好。

2 基于单视几何的身高测量算法的设计

通过计算可得到最小二乘法的解为：

求出m的值后就可将物点的像素坐标带入到公式(3)中从而求得像素点对应的世界坐标，求得平面内两个点的长度，其长度公式为：

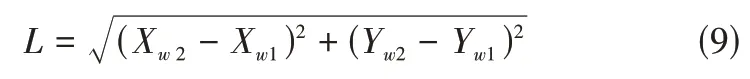
在同一图像平面内，知道四个点的像素坐标和对应的世界坐标便可求得m,利用图像上人物最高点、最低点的像素坐标和公式(3)就可以求出人物最高点和最低点的像素坐标对应的世界坐标，进而达到测量人体身高的目的。本文设计的身高测量算法有以下步骤：

(1)图像灰度化处理。首先对带测量的人物图片进行灰度化处理，相对于彩色图像而言，将图像转化为灰度图像的意义主要有两个，一是相比彩色图像，灰度图像所占的内存更小，运算速度更快；二是转化为灰度图像后可以在视觉上增加对比，突出人体的目标区域。

(2)进行相机标定。获取目标图像中任意四个点的像素坐标，在现实世界中进行测量计算四个点对应的世界坐标，利用公式(8)求出m的值，知道图像中像素坐标系和世界坐标系之间的映射关系。

(3)计算人体的身高。在求得m的值后，获取目标图像中人物最高点和最低点的像素坐标，并将其带入公式(3)中求得人物最高点和最低点对应的世界坐标，利用公式(9)求出计算出人体的身高，达到测量目的。

3 实验结果与分析

本文运用单视几何算法在Matlab 平台上编写程序实现对人体身高的测量，在5幅图像上进行测试，图像编号为图a到图e。在图像进行测试时，首先要选取每幅图像上四个点的世界坐标，在选取世界坐标后，通过鼠标选取世界坐标在图像中对应的像素坐标，计算出m的值，然后通过鼠标获取目标图像中人物最高点和最低点的像素坐标并求出对应的世界坐标，利用公式(9)计算出人体的身高。

为了更好地验证测量算法的有效性，对五幅图像中的每幅图像进行了三次测试，取测量的平均值与真实身高来计算相对误差，测试结果如表1所示。

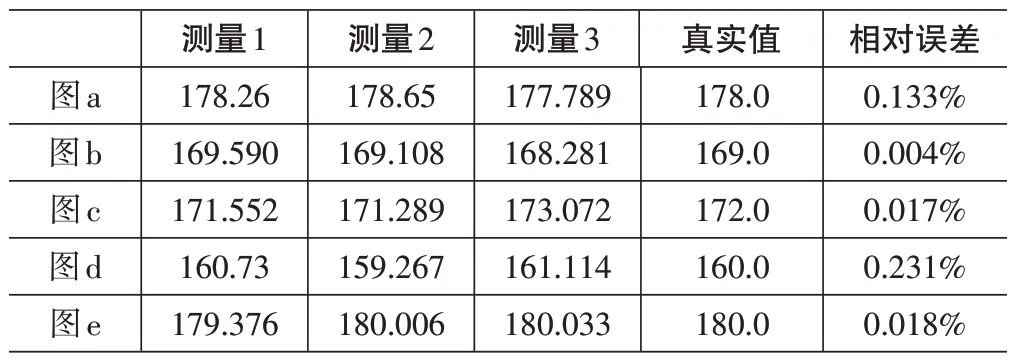
表1 测试结果及相对误差

由表1 可以看出，测量的相对误差在0.231%以内，测量效果较好，能够满足测量要求。但测量结果与真实值之间还是存在误差，分析其产生的原因主要有：(1)图像中四个顶点的世界坐标为手动测量，存在一定误差，图像中四个顶点的像素坐标和人身体最高、最低点的像素坐标也是手动获取，存在一定误差；(2)拍摄图片的角度和目标人物身体的站姿也会导致误差的产生。因此，产生误差的原因有多个方面，以后的工作主要致力于对该算法测量的准确度进行深入的研究。

4 结束语

本文主要是以单视几何为基础设计身高测量的算法，整个身高测量算法的实现在以Matlab 中完成。该算法的设计思路就是建立图像坐标系和世界坐标系，根据单视几何方法求得图像坐标系和世界坐标系之间的映射关系，并根据这种映射关系，在图像上取目标人物最低点与最高点的像素坐标并将其转换成世界坐标，利用两点间距离公式即可测得图像上人体的身高信息。与传统身高测量方法相比，该算法具有成本低、测量速度快、准确度高等特点。对于其他的测量领域来说，该方法具有一定的借鉴意义。