有限长序列循环卷积的求解

任蕾

(上海海事大学信息工程学院，上海 201306)

1 引言

线性卷积和循环卷积是信号处理类课程教学的重要知识点。二者的定义、常用性质、计算方法和异同点也是教学的难点之一。离散线性时不变系统的零状态响应可通过激励序列与系统的单位脉冲响应卷积求得。

陈辉金在文献1中提出了圆周卷积的竖式求解方法，该方法的本质是在线性卷积的对位相乘法基础上拓展而来的，利用了圆周卷积是线性卷积的周期延拓这一结论，该方法简单易学，便于学生理解圆周卷积的本质[1]。文献2 在分析循环卷积与线性卷积关系的基础上提出了一种基于序号和匹配的简单循环卷积求解方法[2]，该方法与文献1的方法本质是一致的，充分利用了参与卷积的序列之间的关系。文献3 则从线性卷积和循环卷积的基本概念入手，探讨了其运算规则和等价条件，并提出了一种利用线性卷积快速计算循环卷积的方法[3]。此外，与科研相结合的循环卷积的教学探讨也有相关报道。戚晨皓等结合通信中的正交频分复用技术，介绍了循环卷积的应用[4]。文献5 结合水声通信领域的应用，介绍了基于线性卷积的循环卷积计算方法及其在该领域的应用[5]。

目前常用的循环卷积计算方法主要包括定义法、图解法、列表法、对位相乘法、变换域方法、矩阵矢量相乘法、Matlab 求解等。特别的有限长序列的卷积是实际数字系统中常见的运算，其卷积结果仍是有限长序列。本文首先介绍线性卷积和循环卷积的基本定义，进而针对有限长序列的循环卷积的计算进行方法总结和梳理，并结合实际例子说明各类方法的应用过程。

2 线性卷积与循环卷积

2.1 有限长序列的线性卷积与循环卷积

有限长序列x1(n)(0≤n≤N1-1) 和x2(n)(0≤n≤N2-1)的线性卷积[6]yl(n)为：

即两个有限长序列的线性卷积，其序列长度不会超过N1+N2-1。

上述两有限长序列的L点循环卷积[6]yc(n)定义为：

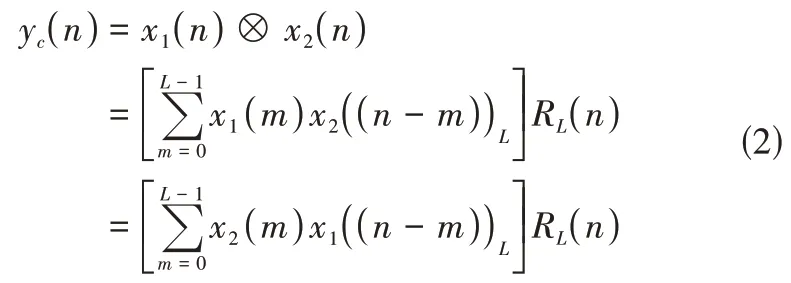
则两有限长序列的循环卷积与线性卷积的关系[6]为：

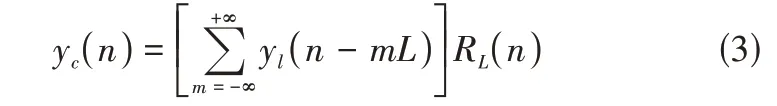
即循环卷积是线性卷积以L为周期进行延拓后构成序列的主值序列。当满足L≥N1+N2-1时，循环卷积和线性卷积一致，否则，部分时刻的卷积和序列会混叠。

2.2 循环卷积各类计算方法总结及对比

考虑到循环卷积与线性卷积的联系，有限长序列的循环卷积可借鉴线性卷积的方法实现，包括定义法、图解法、对位相乘法、矩阵矢量相乘法、变换域方法和利用Matlab的求解方法等。表1 总结了目前有限长序列循环卷积的主要求解方法[1-3,6]，并对其进行简要介绍。

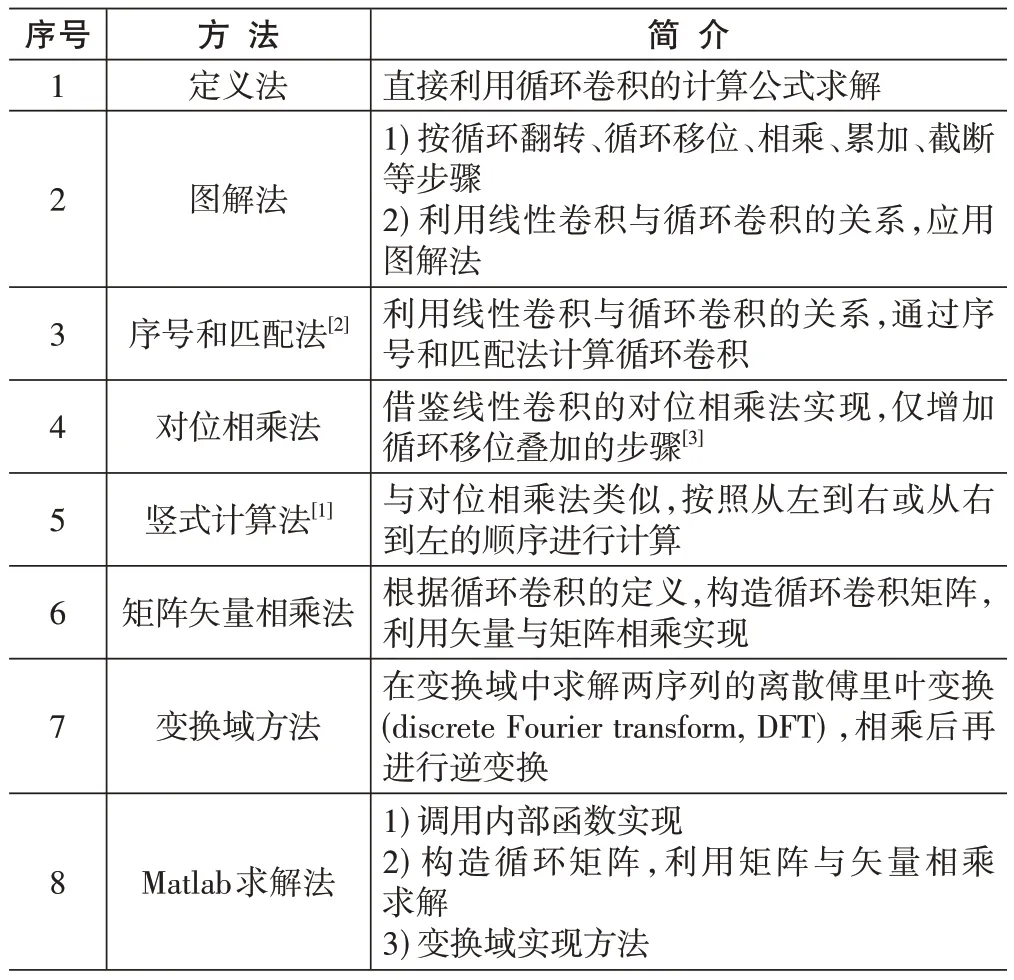
表1 有限长序列循环卷积求解方法总结表

上述方法中基于定义式的计算方法直接从定义出发，是最基本的一类方法，过程较为烦琐。对位相乘法、竖式计算法、序号和匹配法以及图解法等这类方法均是基于循环卷积的基本定义，对参与卷积的序列进行适当的排序、移位、相乘和叠加来进行的，其本质是一致的，只是在序列的排列和计算顺序上有所区别。其中，基于线性卷积和循环卷积关系的对位相乘法最直观简便，可以直接从线性卷积的结果进行适当的循环移位及叠加后得到循环卷积结果。

矩阵与矢量相乘法，其关键是构建循环卷积矩阵[6]，由式(2)定义循环卷积矩阵：

则循环卷积得到的序列yc(n)可由矩阵C与x1(n)构成的列矢量相乘求得：

同理，由交换律，也可由序列x1(n) 构造相应的循环卷积矩阵来实现计算。

变换域方法，则首先计算补零后的x1(n)和x2(n)的L点DFT，分别为X1(k)和X2(k)，其结果逐点相乘并进行逆变换求解循环卷积序列，该方法可借助快速傅里叶变换实现。

最后，应用Matlab 软件也是求解循环卷积的常用方法，根据是否直接调用内部函数可以细分为直接调用方法、矩阵矢量相乘法、变换域实现方法等。Matlab 中的循环卷积内部函数为：cconv(a,b,n)，其中a和b是参与循环卷积运算的序列矢量，n是循环卷积的点数。其他两类情况则需要编写相关的程序实现，详见文献6的相关章节[6]。

3 有限长序列的循环卷积求解举例

本节给出典型例题，并详细介绍几类循环卷积的求解方法。

例题1：已知序列x1(n)=和x2(n)=，计算4点循环卷积y(n)=x1(n)⊗x2(n)。

解：由于文献1-3涉及的方法有类似之处，仅给出文献1的方法以及其他部分方法的求解过程。

1)定义法

4点循环卷积的每一点由下式给出：

2)对位相乘法

这里的对位相乘法是在有限长序列的对位相乘法基础上增加了序列的周期化得到的，即文献1 中所述的竖式计算法，本题的演示过程如图1所示。首先将两序列右侧对齐，第二个序列的每个序列值逐个与第一个序列相乘、移位并求和得到线性卷积的结果，进而根据题意求4 点的循环卷积，则需要将线性卷积结果以4 为周期进行周期化，叠加后的序列选取其0～3时间区间内的结果就是循环卷积结果。从下列过程也可以看出，该方法直观、简便，同时清晰地显示出线性卷积和循环卷积的关系。

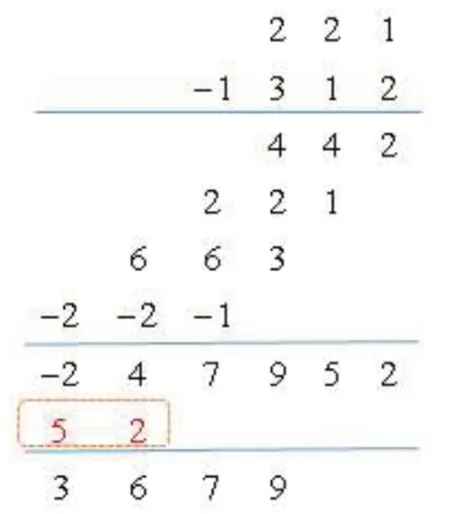
图1 例题1的对位相乘法计算过程

3)矩阵矢量相乘法

矩阵与矢量相乘的方法核心问题是构造循环卷积矩阵，由式(4)可得本题中的循环卷积矩阵为：

4)变换域方法

变换域方法求解循环卷积时，首先需要求解两序列的4点DFT，分别为：

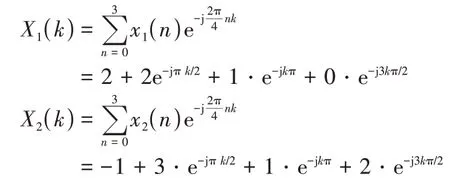
将k=0,1,2,3代入，可得：

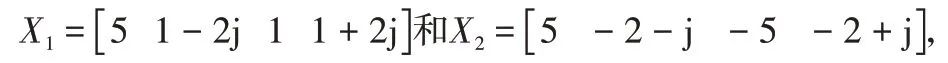
对上述序列进行逐点相乘有：

Y(k)=，因此对其进行逆变换得序列：

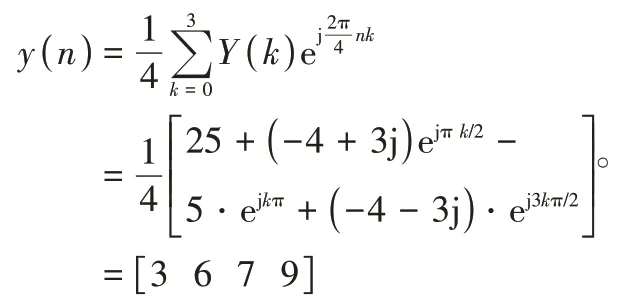
5)Matlab求解方法

Matlab 中的循环卷积的计算函数为cconv(a,b,n)，设置输入参数可以直接求解，本例中两序列、线性卷积和循环卷积的波形如图2所示。

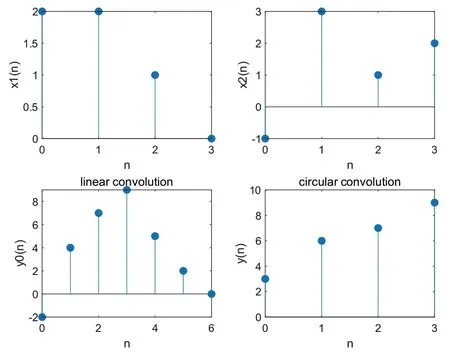
图2 循环卷积的Matlab求解波形图

其次，该例题也可通过变换域方法实现，即分别计算两序列的DFT，在变换域中频谱相乘，再进行逆变换，两信号及循环卷积的序列时域和幅度谱如图3所示。

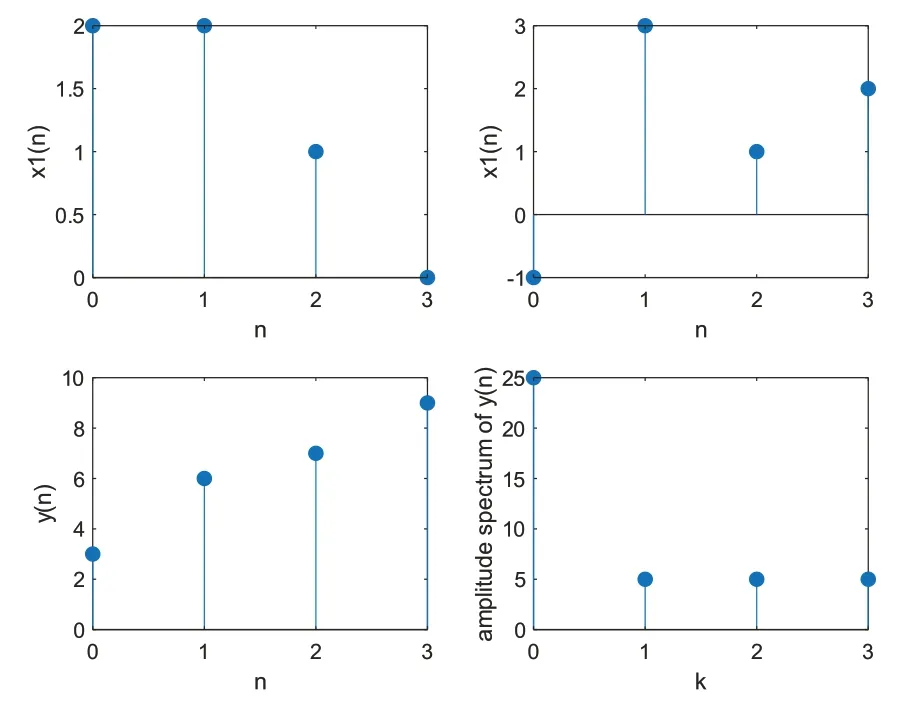
图3 利用DFT求解循环卷积的波形图

再次，在Matlab中也可利用矩阵矢量相乘的方法实现循环卷积的求解，可利用toeplitz函数构造循环卷积矩阵实现。循环卷积实现的程序如下[6]：

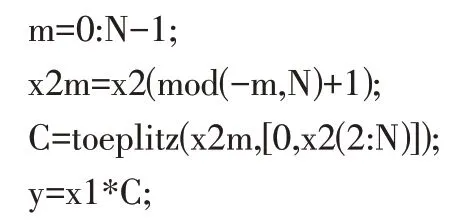
输入已知序列后，应用上述程序也可得到同样的卷积结果。

例题 2：已知序列x1(n)=和x2(n)=，计算8点循环卷积y(n)=x1(n)⊗x2(n)。

解：由于本例中的序列x1(n)和x2(n)的线性卷积序列长度不超过8，因此本例中的循环卷积和线性卷积的结果一致，可借鉴线性卷积的各类方法来求解。

1)列表法

由于列表法是线性卷积的常用方法[6]，按照翻转、移位、相乘、叠加的步骤进行卷积运算，下面给出列表法的计算过程：

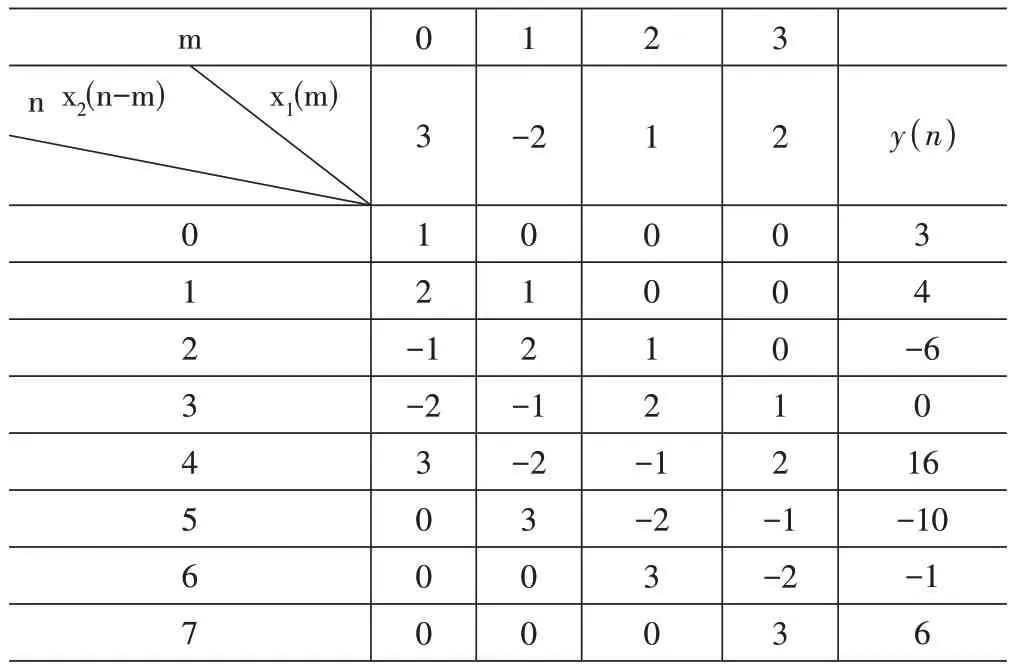
表2 例题2的列表法求解

2)对位相乘法

将两序列右边对齐，依次相乘、移位、叠加，此例题中线性卷积和循环卷积的结果一致。

图4 例题2的对位相乘法计算过程

3)Matlab求解方法

由于本题的特殊性，除直接调用conv(a,b,n)函数实现该例题的卷积运算外，也可通过变换域方法实现，其程序如下所示：

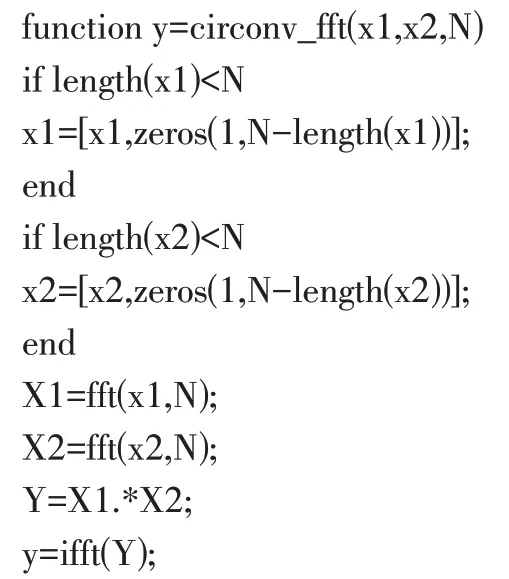
输入序列x1(n)和x2(n)后，应用上述程序可得：y(n)=。该题目中各序列的波形如图5所示：

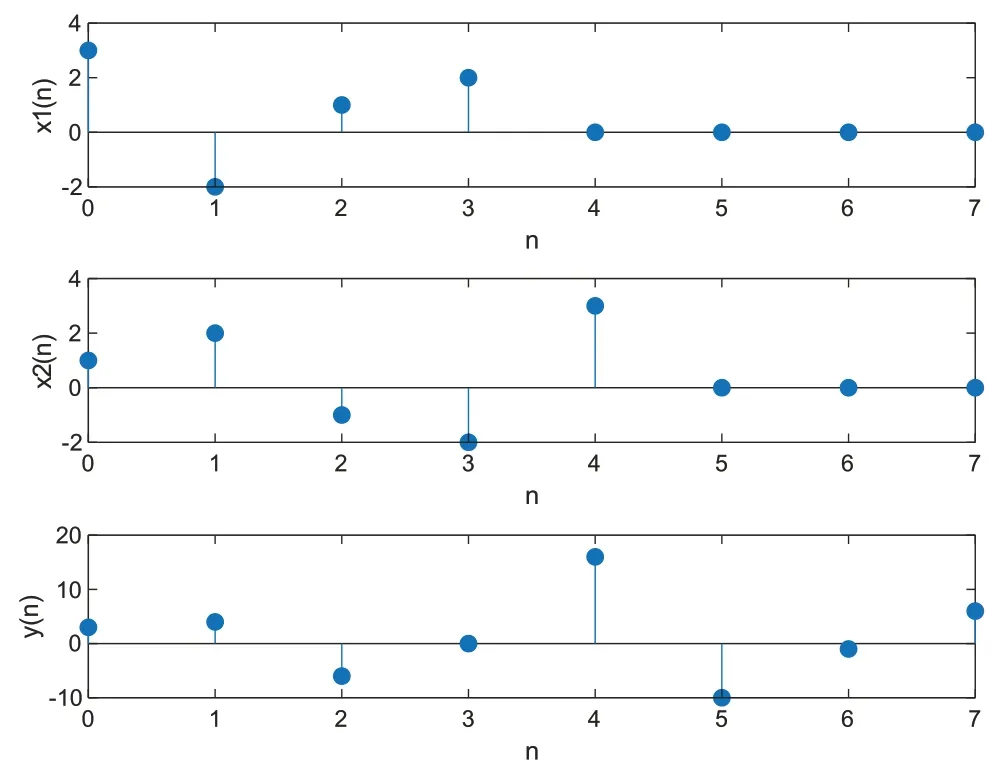
图5 例题2中序列和卷积结果的波形图

上述例题的求解过程再次验证了线性卷积和循环卷积的关系，以及此类运算的本质。对应不同的求解思路，在Matlab中也有相应的实现方法，即可直接调用内部函数，也可通过变换域方法、矩阵矢量相乘的方法来求解。若循环卷积的点数大于等于线性卷积的长度时，则可应用线性卷积的方法直接计算获得。

4 结束语

循环卷积是数字信号处理课程中的重要知识点，也是本课程学习的难点之一，循环卷积与线性卷积有密切联系，当循环卷积的点数大于等于线性卷积长度时，二者结果一致，否则会发生混叠，因此利用循环卷积求解线性卷积时，需注意点数的选择。利用循环卷积的定义及其与线性卷积的关系，本文梳理并总结了已有的有限长序列循环卷积的各类求解方法，并给出了相关例题，以帮助学生掌握并理解循环卷积的基本特点和求解思路。涉及到的方法也是信号处理课程中各类信号和系统分析的常用思路，包括时域和变换域等，此类方法总结也有利于学生融会贯通，从整体上更好地掌握所学知识。