基于改进压缩感知的MIMO雷达成像算法

雷蕾，李彩月，冯俊杰

(六盘水师范学院物理与电气工程学院，贵州六盘水 553004)

多输入多输出(Multiple Input Multiple Output,MIMO) 雷达近年来受到广泛关注[1-2]。MIMO 雷达利用多个天线发射正交信号，并通过多个接收天线对目标发射信号进行接收，对来自目标的反射信号由多个接收天线进行联合处理，形成虚拟阵列，可以极大地提高目标成像的分辨率。根据布阵方式不同，MIMO 雷达可分为集中式MIMO 雷达和分布式MIMO 雷达两类。集中式MIMO 雷达的发射天线和接收天线之间的距离相对雷达与目标之间的距离短，可以形成大的虚拟孔径，提高对目标的探测和跟踪能力。分布式MIMO 雷达其发射天线之间和接收天线之间的距离与目标和雷达之间的距离相当，主要用于目标的参数估计。MIMO 雷达作为新体制雷达，可以提高目标分辨率，实现高精度目标识别，一经出现就成为研究的热点。传统的MIMO雷达成像算法主要基于匹配滤波方法，可以通过单次快拍实现高分辨率成像，从而避免了复杂的运动补偿，但所需天线的数量一般较大。因此，设计单次快拍实时成像且需要较少天线个数成像算法有着重要意义。

近年来，压缩感知(Compressive Sensing,CS)已成为一种新的理论在信号处理领域得到广泛的应用[3-4]，突破了传统奈奎斯特采样定律的限制。该理论表明，只要信号在一定的变换域内具有可压缩或稀疏特性，则可以通过最优化理论从较少的观测值中精确重构出原始信号。该理论是一种利用信号的先验稀疏特性来提高信号重构的理论。MIMO 雷达成像场景中，目标相对于成像背景具有较高的稀疏性，因此，基于压缩感知理论的雷达信号处理得到了广泛的研究[5-10]。

压缩感知重构算法中，基于L0 (向量中非零元素的个数)优化算法能较好地描述稀疏信号的稀疏性，但基于L0 范数的稀疏信号重构算法计算复杂。因此，Mohimani等人提出了平滑L0范数压缩感知重构算法[11]，该算法是利用带参数的高斯函数序列作为平滑函数来近似最小L0 范数，通过控制参数趋近0，实现优化求解，该算法成为平滑L0 范数稀疏信号重构算法(Smoothed L0 norm,SL0)。

该算法采用双层循环结构优化求解，外层建立从大到小的参数序列σ1,σ2,…,σJ，内层采用最速下降法获得近似解。提出一阶负指数函数序列作为平滑函数，采用单环结构代替双环层，增加了参数σ的搜索次数，不影响重构效率的基础上提高MIMO雷达成像效果。

1 MIMO雷达成像信号模型

假设目标位于远场，信号模型采用文献[12]中的模型。MIMO雷达有M个发射天线，有N个接收天线，采用集中式布阵方式，即同一目标相对于每个发射天线和每个接收天线的方向角相同。令cm表示第m个发射天线发射的编码信号，则基带发射信号为：

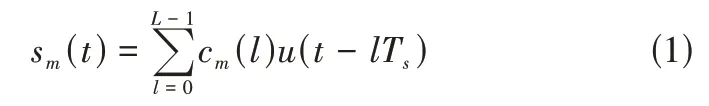
其中T0为子脉冲周期，L为编码长度。假设第m个发射天线的发射信号表示为：sm(t)ej2πft，则经第k个目标反射，第n个接收天线接收信号为：

上式可表示为如下矩阵形式：

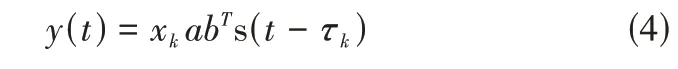
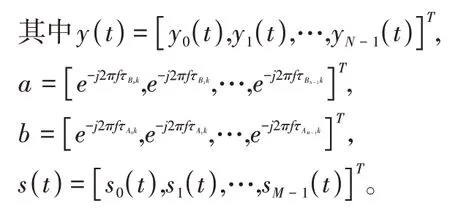
经过离散采样后，接收信号可以表示为矩阵形式S。令x=vec(S)，wk=vec(abTs(t-τk))，vec(•)表示向量化，则有y=xkwk。

假设将MIMO 雷达成像区域划分为多个网格，则MIMO 雷达接收信号的稀疏基矩阵可以表示为：Ψ=[w1,w2,…]，幅值向量可以表示为：x=[x1,x2,…]T，

其中n表示噪声向量。

则采用压缩感知重构算法求解MIMO雷达成像：

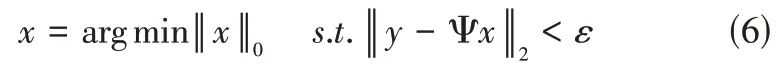
其中为一较小常量，其值与噪声方差有关。

2 改进MIMO雷达成像算法

为求解x，Mohimani等人提出了平滑L0范数稀疏信号重构算法。高斯函数Fσ(x)=作为平滑函数，通过控制参数σ求解最优解，Fσ(x) 由L2范数趋近于L0范数。为进一步提高MIMO 雷达成像质量，本文采用负指数函数Gσ(x)=作为平滑函数趋近于L0 范数。当参数σ从无穷大变为零时，Gσ(x)由L1范数趋近于L0范数，在初始迭代时，本文所使用平滑函数Gσ(x)较高斯函数Fσ(x)具有较大的优势。SL0范数重构算法包含两个循环，在外循环中，控制参数σ由大到小变化，使得平滑函数趋近L0范数解。在循环中，对于每个σj值，求解平滑函数的梯度，然后沿着负梯度方向移动一小步，以获得平滑函数的最小值。但内循环目的是为外环提供初始值，因此本文省略内循环，采用单循环结构，同时减少σj和σj+1之间的搜索间距，增加循环次数。这个算法可以表示为：

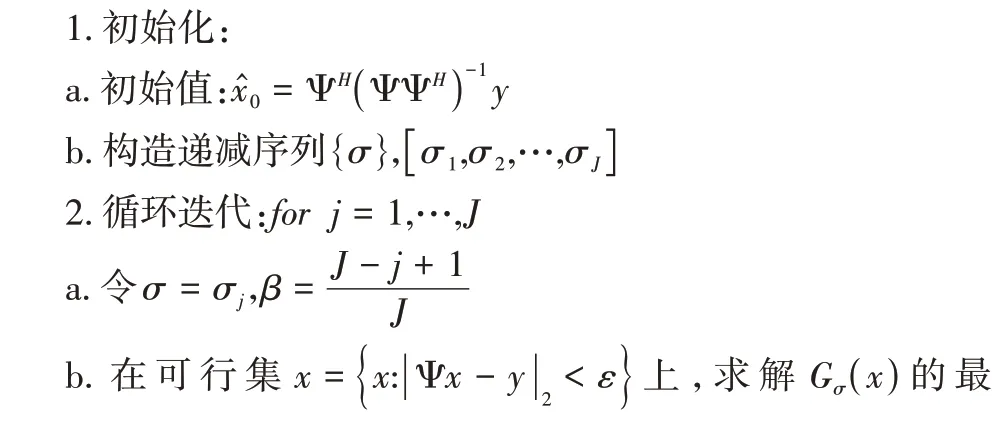
对于搜索步长μ不应过大或过小，如果过大会漏掉部分搜索点，如果过小则增加计算量。本文采用自适应调整步长，μ=，随着循环次数的增加，当搜索点接近最小解时，逐步减少搜索步长，逐渐接近最优值。

3 仿真实验

仿真1：假设目标为理想散射点，孤立位于成像场景中，并且位于所划分的网格点上。MIMO雷达参数为：发射天线、接收天线个数均为8，中心频率f=10GHz，带宽为150MHz，发射阵列和接收阵列为均匀分布的线阵，发射阵元和接收阵元的间距分别为60m和10m。目标与雷达之间的距离为100km。目标由20个散射点组成，目标的幅度和位置如图1所示。本文算法循环次数为200。OMP算法、Laplace算法、SL0算法和本文算法的成像结果如图2(a)(b)(c)(d)所示。可以看出，OMP 算法和SL0算法的成像效果较差，重构部分目标幅值有所减少，且有虚假目标。本文算法成像效果优于其他算法，20个散射点的位置和幅值进行了精确重建，获得了较好的成像效果。

图1 目标的位置和幅值

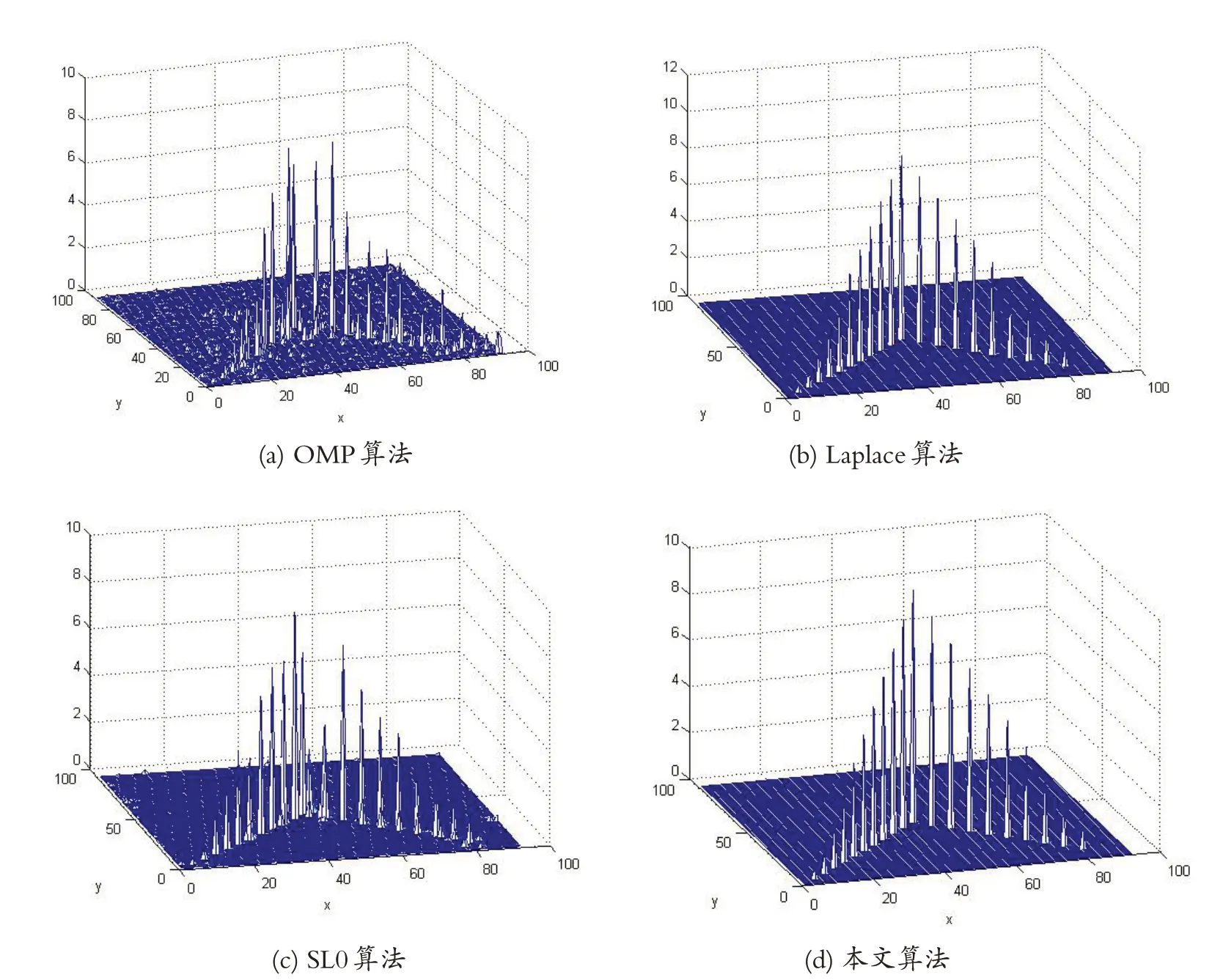
图2 MIMO雷达成像结果

仿真2：在仿真2 中，研究当目标散射点不在点网格上时，采用OMP 算法、Laplace 算法、SL0 算法和本文算法MIMO 雷达的成像效果。MIMO 雷达参数与仿真1相同。目标包含9个散射点，其相对位置为(0,4)、(0.5,0)、(1,6)、(3,3.5)、(4.5,5.5)、(5,2)、(8.5,0.25)、(9,4)、(9.25,4)、(9.25,7.25)(m，m)。目标分布如图3 所示。不同算法的成果结果如图4 所示。可以看出，OMP算法和Laplace算法具有较高的旁瓣，SL0算法成像结果具有虚假目标，对于非网格点的多目标成像，本文算法的成像质量优于其他算法。

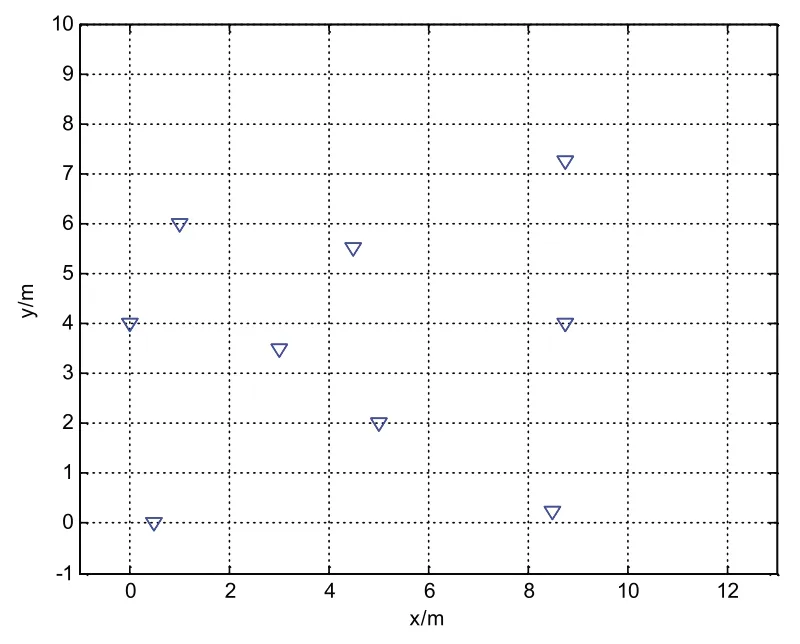
图3 目标的位置

图4 成像结果

4 结束语

压缩感知重构算法可以提高雷达目标成像质量，本文提出了一种基于压缩感知的MIMO雷达成像算法，采用负指数函数作为平滑函数趋近于L0范数最优值，采用单循环结构优化求解，在不增加计算量的基础下保证了重构精度。仿真结果表明，本文算法的MIMO雷达成像效果优于其他算法，具有一定优势。