基于决策树的银行目标客户预测算法

夏安林，杜董生，盛远杰，刘贝

(淮阴工学院，江苏淮安 223003)

1 引言

互联网金融的兴起，使人们在日常消费中的支付更加便捷，为人们的储蓄和借贷服务带来了极大的方便和高效。在互联网金融的冲击与推动下，传统银行既要面对困难，也要面对机会。为了在日趋激烈的竞争中取得有利地位，传统银行应从根本上适应时代发展的潮流和需要[1]。由于网络金融产品在利率、费用、时间等方面相对于传统银行理财产品具有明显的优越性，因此，人们更愿意选择将存款资金投资到网络理财产品中，从而导致了银行客户资源的大量流失。而银行是传统的金融业，虽然有着庞大的用户基数，却不能完全利用这些数据，因此，大量的数据并没有给银行提供更多的信息，更没有发现海量的有用资料。

大数据时代，以互联网、大数据、人工智能为代表的信息技术与各行各业的结合越来越紧密，随着大数据对传统金融行业的革新，我国传统银行面临着新的机遇和挑战[2]。传统银行系统具有丰富的数据量，但是获得的信息却很匮乏，银行许多重要决策依旧是通过经验做出的，而不是根据通过分析数据的结果科学决策，因此利用机器学习的方法对数据进行分析，做出科学的决策才能使银行巨大的数据库发挥真正的作用[3]。

决策树是一种广泛应用于数据挖掘的分类技术，通过对顾客进行归类、对顾客进行顾客关系的处理，并采用不同的市场策略，理解顾客的需要，降低顾客的损失，并提升企业的使用效率，降低费用，增加效益。

2 决策树相关理论

决策树是一种实现分治策略的层次数据结构[4]。该算法是一种能够进行分类与回归的高效非参数学习算法。该算法可以从一组具有特点和标记的资料中归纳出一套判别准则，并利用树型的形式将其表示出来，从而求解出一种归类与回归问题，决策树算法的本质是一种图结构。

决策树的产生是一个递推的过程，在三种情况下都会产生回归。一是目前结点所含的所有样品都是一个类，不需要进行分类；二是当前的属性集合为空白，或者在全部的数据中都具有同样的属性值，则将目前的数据作为一个叶子的节点，并且设置它为数据样本最大的一个分类；三是目前节点所含的样本集为空白，无法进行分割，因此，将目前节点作为“叶节点”，设置该节点的类型为其父结点中数据样本最大的一个类。

2.1 CART决策树

CART 决策树的生成包含分裂，剪枝和树选择三个步骤。分裂：分裂过程是一个二叉树划分过程，其特征可以是连续型或离散型的，CART没有停止准则，会一直生长下去；剪枝：利用成本复杂性进行修剪，首先从最大的一棵树中选取子树，然后对其修剪，直至仅有一棵根结点为止，最终生成一棵最优的决策树；树选择：每个剪树枝的预测效果分别采用一组试验集合进行评价(也可以用交叉验证)。

CART 决策树使用“基尼指数”(Gini index) 来选择划分属性[5]。可以通过基尼值来衡量数据集X的纯度。假定当前样本集合X中第k类样本所占的比例为pk(k=1,2,3,…,y)，则基尼值为公式1所示。

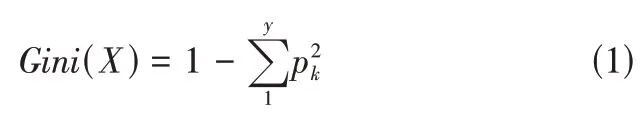
Gini(X) 表明了在两个不同类型标签之间的不一致性的随机抽样的可能性。基尼不纯度是指该样品被选择的概率乘上错误的概率。Gini(X)越小，则数据集X的纯度越高。当一个结点中所有的样本都是一个类时，基尼不纯度为0。

属性a的基尼指数定义为

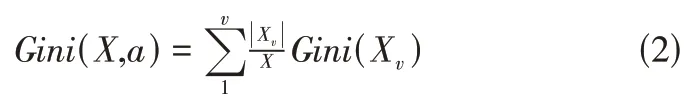
基尼指数Gini(X,A)表示经过A=a分割后集合X的不确定性。基尼指数越大，样本的不确定性就越大。在候选集合A中，选取划分后基尼指数最小的特征作为最佳分割属性，即：

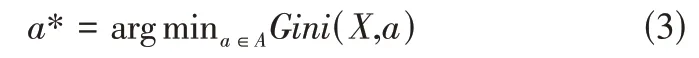
2.2 剪枝

在决策树学习中，剪枝是处理“过拟合”问题的重要方法，为使训练样本得到最准确的归类，需要反复进行分割，导致决策树中出现大量的分支；在这种情况下，由于学习的样本学习太好，以至于将某些特征视为所有的资料都具有的普遍特性，从而造成了过度拟合。决策树剪枝的基本策略有“前剪枝”和“后剪枝”[6]。

前修剪算法是将决策树的结构预先终止而进行修剪，因为它不能预先得到停止的临界点，因此不经常采用。后修剪技术是在决策树发育成熟后，将一些结点上的分叉修剪，从而实现了对大型决策树的裁剪。最有代表性的后修剪方法是成本复杂度修剪。其基本思想是：对每个内部的结点进行运算，假设结点的子树经过修剪后，可以得到预期的错误率。在修剪后，如果期望错误率增加，就会保持这个子树，否则就修剪这个子树。该算法生成了一套修剪过的树，然后利用一套单独的试验系统对树进行评价，最后正确率最高的树被保留为结果。

3 基于决策树算法的银行客户预测

通过对数据集的预处理，采用决策树模型对数据进行归类，并对其进行评估、分析，并将其与原始模型进行对比，然后利用该模型对数据进行了预测。测试流程包括：数据预处理，决策树分类训练集，用训练后决策树模型进行预测，并将其输出。

3.1 数据预处理

该文以银行机构直接营销的海量真实数据，分析各类属性预测客户是(1类)否(0类)会购买定期存款(y)，所有决策属性中还有客服人员与客户联系的信息以及其他属性。

本数据集共有25317行，18列。前几行示例如表1所示。

表1 数据集示例

数据说明如表2所示。

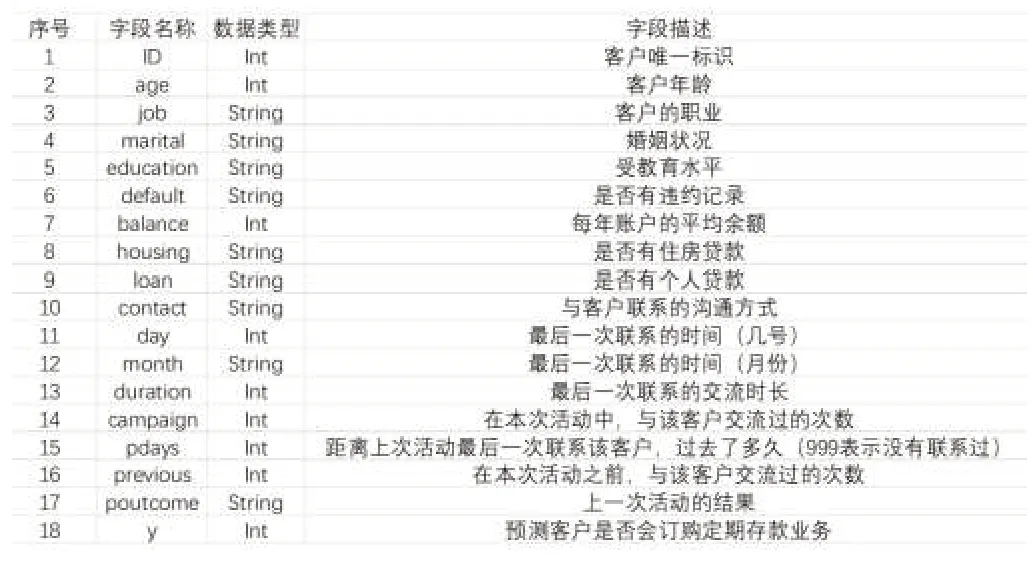
表2 数据说明

其中，客户唯一标识(ID)和预测客户是否会订购定期存款业务(y)不作为分类属性，则选择的分类属性共有16种，选择预测属性一种(y)。在选定了这些属性之后，每个属性都会被检查规范性和合理性，并且筛选出合格的属性。

首先区分出连续型和离散型属性，其中连续型属性有{age,balance,day,duration,campaign,pdays,previous}，离散型属性有{job,marital,education,default,housing,loan,contact,month,poutcome}。

对每个连续属性绘制箱线图查看离群点的分布。可以提供数值型变量的最小值、最大值、四分位数、中位数和的值。将n 个数从小到大排序，四分位数是四分位置对应的数，以此类推：

下四分位：Q1=(n+1)/4

中分位：Q2=(n+1)/2

上四分位：Q3=3(n+1)/4

四分位距：IQR=Q3-Q1

上界：Q3+1.5IQR

下界：Q1-1.5IQR

通过图1所示的箱线图检查连续型属性是否存在离群点。

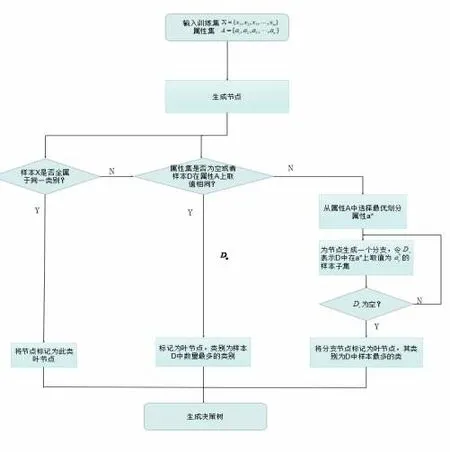
图1 决策树生成流程图

图1 连续型属性箱线图

由箱线图可知：

1)age属性删除大于70的记录。

2)balance删除大于3763和小于-1965的记录。

3)duration属性删除交流时长大于639秒的记录。

4)campaign删除联系数量大于6的记录。

5)day属性没有离群点不做删除。

6)pdays属性为客户最近一次与之前活动联系后经过的天数，pdays属性中有20000 条左右值为-1，剩余越5000 条是不为-1，处于1～854 之间的一些值。这列数据的中位数，上四分位数，下四分位数均为-1，如果删除离群点，这个属性全为相同值，就没有意义了，所以不做删除。

7)previous此活动开始前与客户的联系数量，previous属性中有20000 条左右值为0，剩余约5000 条是不为0，处于1～275之间的值，此列属性的上四分位数，下四分位数和中位数都是0，所以也不做删除。

对于离散型的变量，存在一些值为unknown的值，首先是进行频率的统计，将少量的数据进行剔除，大量的删除会对分类的结果造成一定的干扰。

离散型的变量中存在值为unknown的有以下属性:

1)job工作类型，unknown值较少，进行删除。

2)education教育水平，unknown值较少，进行删除。

3)contact联系人通信类型，unknown值有7000 多条，为了避免影响结果，所以不做删除。

4)poutcome以前的营销活动的结果，unknown值有20000多条，为了避免影响结果，所以不做删除

不存在unknown值的离散型变量有以下属性：

1)marital婚姻状况,三个取值，无异常值。

2)default，二元变量，无异常值。

3)housing是否有住房贷款，二元变量，无异常值。

4)loan是否有个人贷款，二元变量，无异常值。

5)month每年的最后一个联系月份，十二个月份，无异常值。

3.2 建模过程

决策树分类方法适合银行数据量大、数据属性多等特性[7]。以3/4 的数据集为训练集合，1/4 的数据集作为测试集合，利用混淆矩阵中的各个度量指标和ROC 曲线来观测模型的错误率，并对测试集合进行预测。

该文采用CART决策树，剪枝后决策树可视化如图2所示。除了叶节点之外的所有节点都由五个部分组成。基于一个特征的值的有关数据的问题。每个问题的答案要么是True，要么就是False，根据问题答案数据点会在该决策树中移动；gini：基尼不纯度；samples：节点中的数量；value：每一类别中的数量；class：节点中大多数点的类别。

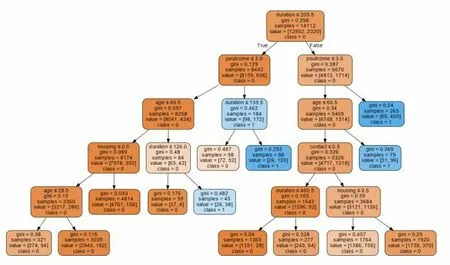
图2 决策树可视化图

通常使用混淆矩阵来描述决策树的性能，建模结果如表3所示。

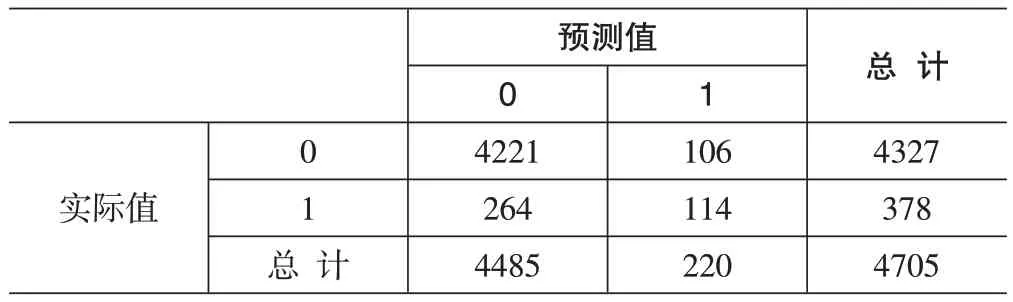
表3 混淆矩阵

根据上表混淆矩阵可得以下指标：

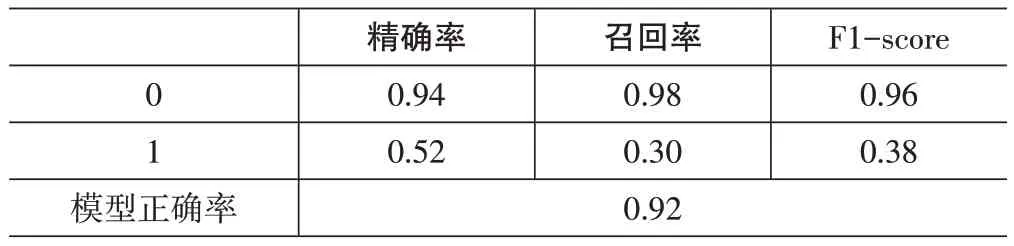
表4 模型准确率

其中，精确率为分类正确的数目与分类器判定为该类的数目所构成的比率，召回率为分类正确的数目与该类实际样品数量的比率，F1-score是精确率与召回率的协调平均。

结果表明：该模型具有92%的准确率，但1类样品中只有30.1%的数据被正确分类，从图3的ROC曲线可以得出ACU 为0.89。因此，所建立的模型不够完善，需要对其进行优化，以克服数据不平衡的问题[8]。

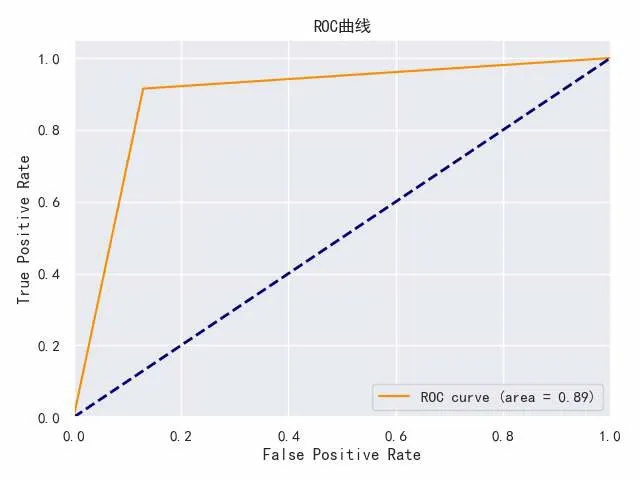
图3 ROC曲线

3.3 模型优化

采用决策树对不平衡的数据进行分类预测，总体准确率虽然高，但1 类预测准确率偏低；就银行来说，对1 类数据错误的判断会产生很大的影响，在这个案例中，1 类顾客很有可能会订购银行的定期存款，但是，模型认为顾客不太可能订购。这种数据不均衡的情况下，通常可以用采样技术解决。

首先，对数据进行过采样、欠采样、人工合成法进行数据处理，得到的数据如表5所示。

表5 采样数据分布

从表中可以看出，在采样技术的作用下，两种类型的数据均得到了平衡，建立决策树模型，结果如表6所示。

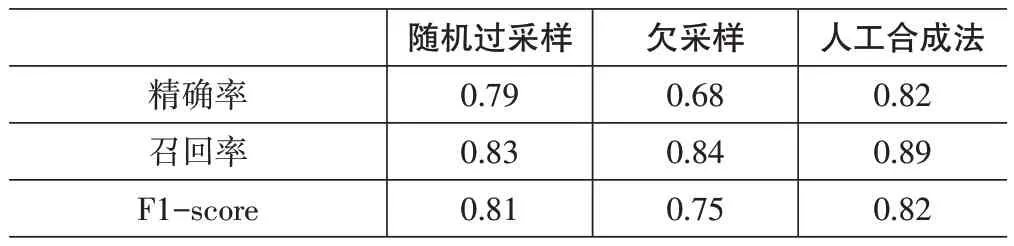
表6 采样后模型1类准确率

由表6可知，模型的总体准确率相比之前有所降低，但1类样本召回率有了极大的上升，1类样本的预测正确率大幅提高，为了在最小的代价下获得最优的准确度，一方面考虑1类正确率带来的客户效益，另一方面考虑0类正确率带来的成本效益，因此采用人工合成法处理得到的数据集训练模型，由图4优化后ROC曲线可得ACU值提高到0.98，模型测试结果较为满意。

图4 优化后ROC曲线

最终得到的决策树如图5所示。

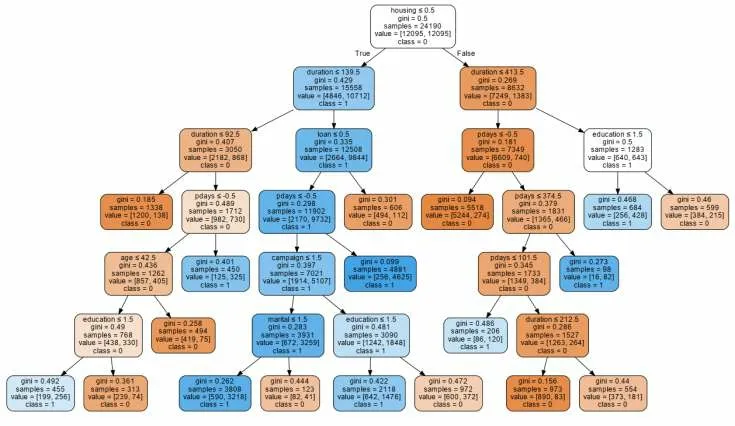
图5 优化后决策树可视化图

4 结束语

互联网金融的产生与发展对于银行业存款业务产生了巨大的冲击，如何有效地控制成本的同时增加其自身竞争力尤为重要[9]。银行具有巨大的数据库，对客户信息挖掘有着极大的优势，对于客户信息的提取与挖掘对于银行制定差异化策略具有很大的参考意义，在对客户存款营销时，如何能够在成本最小化，利润最大化的情况下拉到更多存款对于银行来说有着重要意义。

该文介绍了CART决策树算法，同时提出了在数据预处理过程中对数据缺失值、不一致值、噪声数据的处理及对于不均衡数据的处理方法。首先将数据进行预处理，剔除了噪声数据以及不一致数据，同时运用采样方法解决了不均衡问题，最后运用的是CART 算法建立决策树并最终得到了预测结果较好的模型。