行简化阶梯形矩阵的Excel VBA程序实现

毛圆洁

(无锡科技职业学院基础部，江苏无锡 214028)

行简化阶梯形矩阵在线性代数中有着重要的作用。将矩阵转化成行阶梯形矩阵，能够计算矩阵的秩，判断方阵是否可逆，判定向量组的线性相关性。将矩阵转化成行简化阶梯形矩阵，可以快速找出向量组的极大无关组，并且写出其余向量用这个极大无关组的线性表示，不仅如此，将线性方程组的增广矩阵转化成行简化阶梯形矩阵，可以写出线性方程组的唯一解、无解或者无穷多解。计算行简化阶梯形矩阵贯穿了线性代数的矩阵、向量组的线性相关性、求解线性方程组等多个章节的学习，在传统的线性代数教学中，将矩阵转化成行简化阶梯形矩阵通常采用初等行变换的方法来计算，人工计算占用时间多，计算量大，效率也不高。本文借助常用软件Excel，设计了一款行简化阶梯形矩阵的计算程序，实现了矩阵行简化阶梯形的一键智能化[1]。

1 相关定义

定义1 若一个矩阵的所有零行在非零行之下，且非零行的首非零元素所在列在上一行(如果存在的话)的首非零元素所在列的右面，则称此矩阵为行阶梯形矩阵。

定义2 若一个矩阵是行阶梯形矩阵，并且非零行的首非零元素为1，首非零元素所在列的其余元素都为0，则称该矩阵为行简化阶梯形矩阵[2]。

2 行简化阶梯形矩阵的算法与Excel VBA程序实现

2.1 算法

根据定义，行简化阶梯形矩阵非零行的主元素所在列的其余元素必须是零，所以第一步，可以按矩阵的行开始循环，找到每一行的非零首元素，将非零首元素所在列的其他元素通过初等行变换的倍加变换都化为零。第二步，找到每一行的非零首元素，利用初等行变换的倍乘变换将它们都化为1。经过前两步的计算，此时矩阵已经与行简化阶梯形矩阵非常相似，该矩阵只要通过交换行便可转化为行简化阶梯形矩阵。所以第三步，将零行放在矩阵的最下方，非零行的主元素所在列要按照从小到大，从左往右的顺序排列，保证所有非零行主元素都在上一非零行(如果存在)主元素的右侧。通过这三步，即可将任意矩阵转化成行简化阶梯形矩阵[3]。

2.2 Excel VBA程序实现

根据算法设计，给出行简化阶梯形矩阵实现的具体程序[4-6]：

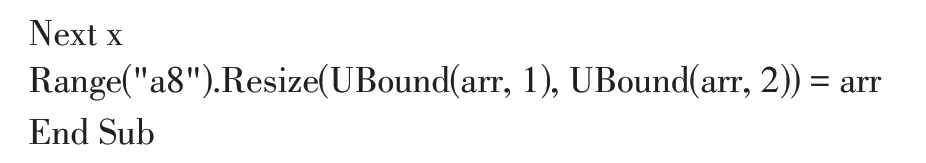
3 应用举例

例1 计算向量组α1=(1,2,1,0)，α2=(2,5,3,2)，α3=(-1,2,-6,8)，α4=(0,3,3,6)，α5=(4,5,0,-6)的秩，求一个极大无关组，并将剩余向量由极大无关组线性表示。

在Excel 的A1 至E4 单元格内依次输入向量组α1,α2,α3,α4,α5，选中A1 至E4 单元格后，左键单击“开发工具”——Visual Basic，在通用窗口内运行本文2.2中的VBA程序，运行结果如图1所示。

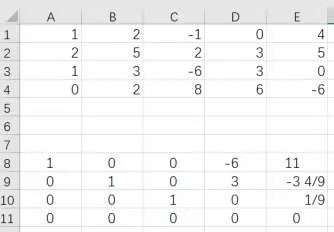
图1 例1程序运行结果

A8 至E11 单元格返回了例1 中向量组的行简化阶梯形矩阵，非零行的行数为3，因此，r(α1,α2,α3,α4,α5)=3。根据主元列所在位置得到向量组的一个极大无关组为α1,α2,α3，其余两个向量α4,α5可以由这个极大无关组线性表示为：α4=-6α1+3α2，α5=11α1-。

例2 求下列非齐次线性方程组的通解：

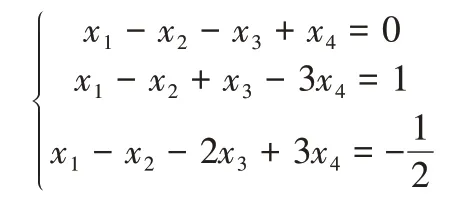
在Excel的A1至E3单元格内输入线性方程组的增广矩阵，选中A1至E3单元格后，左键单击“开发工具”——Visual Basic，在通用窗口内运行本文2.2中的VBA程序，运行结果如图2所示。

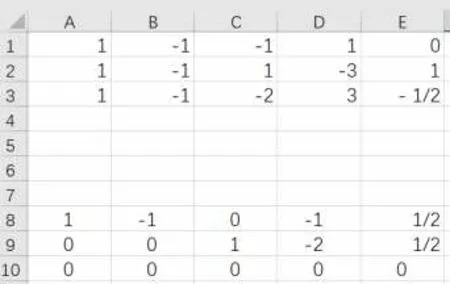
图2 例2程序运行结果

A8 至E10 单元格返回了例2 中线性方程组增广矩阵的行简化阶梯形矩阵，此时方程组有解且为无穷多解，

因此，原线性方程组的通解为：

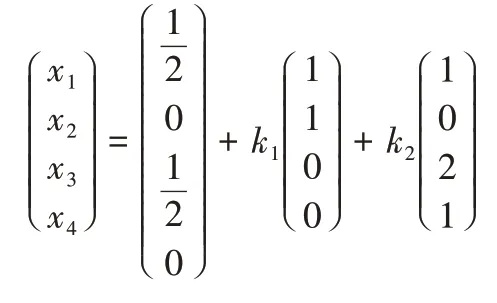
4 总结与讨论

本文设计的行简化阶梯形矩阵转化的程序是基于常用软件Excel 的，考虑到Excel 具有广泛的群众基础，使用携带都比较方便，具有较好的可推广性。对比传统教学的人工计算，本文的设计能大大提高线性代数教学的课堂效率，帮助学生理解一些抽象的数学概念，激发学生的探索兴趣，提升教学效果。Excel 软件本身含有计算矩阵乘积、矩阵的逆以及行列式值的函数，分别为MMULT、MINVERSE和MDETERM，结合本文的设计，基本涵盖了线性代数中行列式、矩阵及其运算、矩阵的初等变换和线性方程组、向量组的线性相关性章节的计算部分，适合开发成与线性代数相配套的计算实验课，增强课程的实用性。