粗晶铝合金高温塑性变形行为研究

韩莹，何实，徐玉君，陈鹏达，韩维超，王雨萱

哈尔滨焊接研究院有限公司 黑龙江哈尔滨 150028

1 序言

近年来，随着工业技术的发展，为了降低CO2排放等能源问题，以铝合金为代表的轻量化合金材料的应用技术已经成为研究的前沿和热点之一[1]。5083是一种典型的铝镁合金，具有良好的强度、成形性能和耐腐蚀性能[2]。国内外先进的轨道交通技术研究中，采用超塑性成形技术是获得铝合金零件的有效途径。不过，在超塑性成形工业应用中，主要面临的一个技术障碍是在超塑性成形前，一般使用多种材料加工方法来实现晶粒的细化，但这种前期晶粒细化不仅使得材料制备变得复杂，还增加了工艺成本。

激活能Q是研究粗晶5083铝合金高温变形的基础，激活能Q对应着金属在变形过程中所需能量，其值大小可与材料的晶界激活能和晶内激活能相对应，结合材料的微观组织变化，可用于分析其变形机理，从而实现轨道交通轻量化，有效节约能源、降低能耗。目前，研究粗晶塑性变形机理有助于降低细晶超塑性对材料的严格要求，省去了繁琐的预处理过程，使超塑性加工技术在生产中得到更广泛应用，具有更直接的经济优势。

2 试验

2.1 试验材料及设备

试验所用10mm厚的粗晶5083铝合金轧制板材的化学成分见表1，材料原始金相组织如图1所示。由图1b可知，垂直于切向的切面TD面晶粒呈柱状形态，柱状长轴沿轧向分布。图1c为原始板材表面ND面的金相组织，采用Image pro plus软件计算得到长轴约233.2μm、短轴约11.8μm，柱状晶横截面截距约87.6μm，相对于一般超塑性对晶粒尺寸的要求（10～15μm）大得多，是典型的粗晶板材。

因塑性变形拉伸量程较长，所以高温拉伸试验试样采用非标试样。取样沿轧制方向，试样尺寸如图2所示。拉伸试验采用的高温拉伸试验机型号为AG-IS 100kN。金相分析在OLYMPUS GX51光学显微镜上进行，观察拉伸后试样的微观结构。

图2 高温拉伸试样

2.2 试验方法

高温拉伸试验参考了国内外类似材料的试验后，采用恒应变速率拉伸法，应变速率在1×10-2～1×10-4s-1之间选定，分别为1×10-2s-1、1×10-3s-1、5×10-4s-1和1×10-4s-1。试验温度为400～475℃，每隔25℃进行一次试验，将温度上升到试验温度后保温15min。高温拉伸试验在空气条件下进行，各做3组试验，取平均值。应变速率敏感指数m值采用logσ-logε˙曲线斜率测定。激活能Q采用双曲正弦函数计算，研究其与微观组织的关系，建立材料的本构方程，讨论塑性变形过程的变形机制。

试样制备过程如下：先使用不同粗糙等级（200#～3000#）的砂纸依次研磨拉伸试样，然后采用电解抛光和阳极覆膜法制备试样。电解液为10%HClO4+90%C2H5OH，电解电压为24V，时间为7s。阳极复膜液为5%HBF4+95%H2O，覆膜电流为1A，时间为60s。

3 结果与讨论

3.1 应力-应变曲线

选取400℃、425℃、450℃、475℃共4组试验温度，根据采集的高温拉伸试验数据绘制应力-应变曲线，如图3所示。

由图3可看出，在应变速率不变时，5083铝合金的应力随着变形温度的增加而降低，在较低变形温度下，粗晶5083铝合金加工硬化速度快而材料内部回复和再结晶软化速度慢，因此在低温度下粗晶5083铝合金加工硬化占主导作用，导致其应力高；随着变形温度的升高，粗晶5083铝合金中原子活动能力增强，位错间的相互抵消导致材料软化程度增大，从而材料的动态回复软化行为占主导作用[3]，随着变形的不断进行，材料的加工硬化和动态回复软化达到平衡，导致粗晶5083铝合金应力趋于稳定，且随着应变速率的增加而降低。

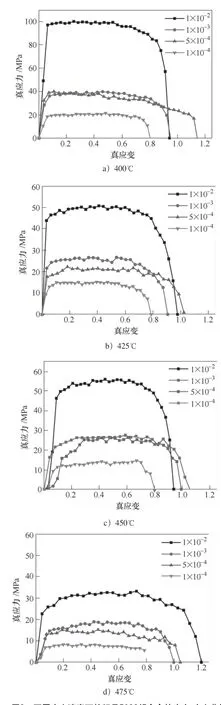
图3 不同应变速率下的粗晶5083铝合金的应力-应变曲线

温度、应变速率及晶粒的大小和结构是影响材料超塑性优劣的主要因素。对于粗晶5083铝合金而言，其晶粒尺寸和组织结构已经确定，主要影响因素是温度和应变速率[4]。通过粗晶5083铝合金单向高温拉伸试验，可以发现材料拉伸试验时的变形激活能会影响材料的超塑性。

当温度为400～475℃、应变速率为1×10-2～1×10-4s-1、粗晶5083铝合金高温拉伸应变ε= 0.3时的应力见表2，采用ε=0.3时的应力计算铝合金的应变速率敏感指数m值。从表2可看出，在同样的变形温度下，应变速率增加，应力增大。当应变速率相同时，应力随温度升高而下降。在低应变速率（1×10-4s-1）时，应力增加缓慢；在应变速率较高（1×10-2s-1）时，应力增加明显[5]。

表2 不同温度和应变速率下试样的应力（ε=0.3）

3.2 微观组织分析

由图3可看出，前期试验在温度为400～475℃时，450℃时的断后伸长率较高，当应变速率为1× 10-2s-1、1×10-3s-1、5×10-4s-1和1×10-4s-1时，该温度下的断后伸长率分别为120%、139.5%、109.5%和94%，因此选取450℃为试验温度进行应变速率对粗晶5083铝合金微观组织影响的研究，如图4所示。

由图4可看出，高应变速率和低应变速率下的组织演变是不同的。微观结构显示出细长和锯齿状的晶界，可以归因于动态回复的发生。当高温拉伸时，在应力和温度的影响下，晶界发生局部迁移。由于这种微观结构是动态回复的特征之一，因此可以推断这种回复机制在这些条件下占主导地位。

如图4a、b所示，粗晶5083铝合金的晶粒尺寸在较高应变速率（1×10-2s-1和1×10-3s-1）的作用下，沿变形方向明显拉长。结果表明，在高温、高应变速率条件下，变形主要集中在晶粒内，这主要是由晶体中的位错滑移造成的。图4a所示的晶界模糊，主要是由于应变速率大，从保温结束到拉断的时间很短，晶粒受到的拉应力过大，位错密度高且没有缓冲时间。此外，还可以发现，当应变速率降低时，在晶界附近观察到非常细的晶粒，说明在1×10-2s-1的拉伸条件下，拉伸断口附近已经开始发生动态再结晶。

图4 应变速率对显微组织的影响（450℃）

因此，动态回复和连续动态再结晶在粗晶5083铝合金的塑性变形中起着重要作用，而不需要通常的细晶粒尺寸为前提。如图4b所示，被拉长的晶粒最均匀，在450℃、1×10-3s-1拉伸时，伸长率最高达到139.5%。此时，动态再结晶继续发生，生成了更多的细小晶粒，且生成的细小晶粒在应力作用下被均匀拉长，无晶界模糊现象。如图4c所示，在5×10-4s-1的低应变速率下，已经析出的细小晶粒随着时间的延长而发生了长大，晶粒在垂直于拉伸方向上明显增大。晶界滑移难以沿细长晶粒的方向发生，晶粒长宽比增大意味着位错蠕变将成为高温变形过程中的变形机制，拉伸试验中占主导地位的变形机制由晶界滑移转变为位错蠕变[6]。如图4d所示，在1×10-4s-1的应变速率下，晶粒继续发生长大，使晶界难以滑移，晶界附近应力集中。当应变速率分别为5×10-4s-1和1×10-4s-1时，伸长率分别为109.5%和94.0%，材料的塑性变形能力降低。

综上所述，当变形温度为450℃时，粗晶5083铝合金伸长率随应变速率的降低而先增大后减小。原因是粗晶5083铝合金在发生塑性变形过程中发生了再结晶和晶粒长大，变形时间随应变速率的降低而增加。随着应变速率的降低，再结晶可以消除加工硬化引起的应力集中，提高粗晶5083铝合金的伸长率。而当应变速率继续降低到5×10-4s-1时，伸长率也发生了降低，这是因为5083铝合金发生了再结晶长大，使粗晶5083铝合金塑性性能降低。因此，其塑性变形机制以动态回复为主。

3.3 应变速率敏感指数m值

材料在超塑性变形时存在稳定变形阶段，此时可进行大的均匀变形，这种均匀变形就是实现超塑性的前提条件，m值作为超塑性变形的重要参数，表征材料变形时流动应力对于应变速率的敏感性，衡量材料在变形过程中能否维持均匀变形的一个重要参数。当0＜m＜1时，m值越小，拉伸试样上产生颈缩的地方变形速度越快，最后便导致试样直接断裂；具有大m值的材料对局部收缩的抗力增大，试样整体呈现出比较均匀的伸长，最终获得较大伸长率。根据m值的定义，在不同拉伸变形条件下测得的稳态流变应力，可获得应力-应变曲线，斜率即为m值。通常认为当m≥0.3时，材料具有超塑性。

对同时具有应变硬化和应变速率硬化的材料，其变形过程应服从C.Rosserd方程[7]，即

式中σ——流动应力（MPa）；

K——常数（材料系数），一般与材料变形温 度、显微组织和结构有关；

ε——真应变；

n——应变硬化指数；

——真实应变速率；

m——应变速率敏感性指数。

当材料处于超塑状态时，因超塑性变形温度＞0.5Tm（Tm为材料熔点绝对温度），n值很小，一般认为n≈0，则式（1）可写为

本试验用测斜率的方法计算m值，在一组同温度、不同初始应变速率条件下的应力-应变曲线上，取同样应变量时所对应的应力σ，并根据初始应变速率ε˙绘出logσ-logε˙变化曲线的斜率即为m值（见图5），两边取对数得到超塑流变方程，又称Backofen方程[7，8]，即

图5 logσ-log ε˙曲线图（斜率为m，ε=0.3）

由图5可知，400～475℃时，流变应力随应变速率变化的图像，流变应力取ε=0.3时的应力，斜率即是对应温度下的m值。以1×10-2～1×10-4s-1的初始应变速率，400～475℃超塑性拉伸温度进行恒温拉伸时，m值平均为0.293～0.354，且随拉伸温度升高，m值略有增大（400℃较特殊）。观察图5纵坐标可发现，变形温度升高，应力减小。

在超塑性变形稳态流变阶段，应力对应变不敏感，而对应变速率敏感，在塑性变形中材料产生强化、松弛等过程时，进行控制和调节，不均匀性才得到转移，m值的提高使得这种控制和调节作用增强。

3.4 超塑变形激活能Q值

变形激活能Q是材料的一个重要参数，主要用于计算代表温度补偿应变速率的Zener-Hollomon参数。除此之外，激活能根据材料来有效预测在给定温度和应变速率下，动态再结晶开始时对应的最大应力和应变值。在理想情况下，激活能Q值仅取决于材料的化学成分和微观结构[9]。一般认为，超塑变形的激活能Q更接近晶界变形激活能，热激活过程可通用Arrhenius[10，11]方程表示，即

式中R——气体常数；

T——绝对温度（K）；

m——相应ε˙和T下的应变速率敏感指数。

应变速率本构方程用3种Arrhenius方程[10，11]来表示，一般情况下，在低应力水平下（ασ＜0.8），幂函数型式（5）适用，在高应力水平下（α σ＞1.2），指数型式（6）适用，Jonas等[12]提出的双曲正弦函数型式（7）在两种情况下均适用。分别计算粗晶5083铝合金的变形激活能，研究变形激活能与温度、应变速率的关系，即

式中——应变速率（s-1）；

Q——变形激活能（J/mol），与材料相关；

σ——流动应力（MPa）；

T——绝对温度（K）；

R——摩尔气体常数，8.314J/（mol·K）；A——与材料相关的常数；

α——应力水平参数，α=β/n1。

两边分别取对数后，整理得到n1、β和n，即

（1）计算材料常数n1、β和n的值 由式（8）可知，ln-lnσ的斜率即为n1，由式（9）可知，ln-σ的斜率即为β。利用最小二乘法线性回归对图6和图7进行线性回归，即可得到本构方程中的n1和β值，各曲线的线性回归结果见表3。

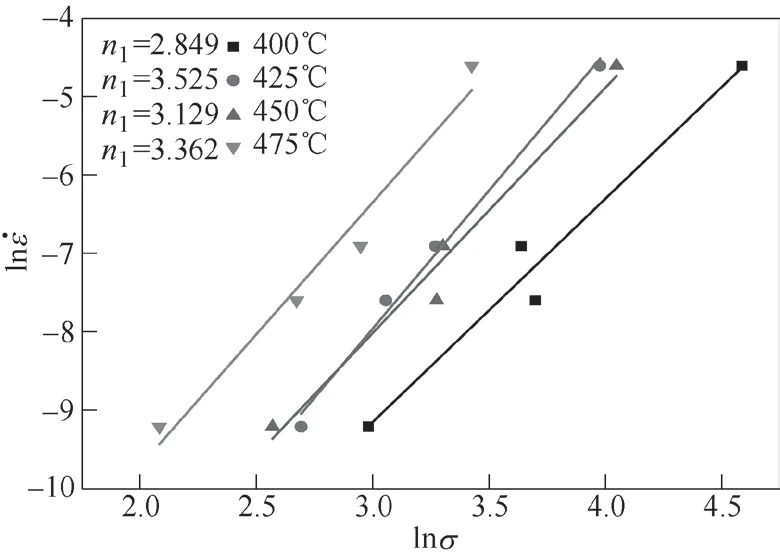
图6 ln -lnσ曲线（斜率为n1）

绘制ln-σ曲线，根据β值划分计算区间。从图7可看出，除了在400℃、1×10-2s-1时，ln-σ的拟合曲线偏差较大外，其余温度及应变速率区间ln-σ均为线性关系。由图7可看到，随着温度增大，β值逐渐增大，在425℃和450℃时，β值变化不大，基本为定值。

图7 ln -lnσ曲线（斜率为β）

由表3可知，n1=3.216，同理，得到β=0.116。由于α=β/n1，即α=0.0354。

表3 ln =A+Blnσ （斜率为n1）和ln =A+Bσ（斜率为β）的一元线性回归结果（ε=0.3）

表3 ln =A+Blnσ （斜率为n1）和ln =A+Bσ（斜率为β）的一元线性回归结果（ε=0.3）

T/℃ B（n1） B（n1）相关系数B（n1）平均值 B（β） B（β）相关系数B（β）平均值 α=β/n1 α=β/n1 0.054 0.898 0.0190平均值400 2.849 0.948 3.216 425 3.525 0.990 0.103 0.921 0.0291 450 3.129 0.964 0.107 0.933 0.0342 475 3.362 0.956 0.199 0.992 0.0592 0.116 0.0354

（2）计算热激活能Q值式（5）～（7）两边取对数后，再分别对1/T求导，在确定的应变和应变速率下，激活能Q值分别由下式求出，即

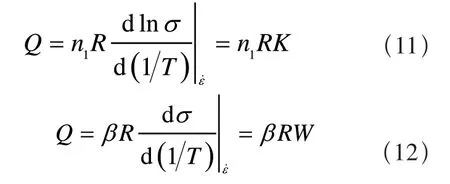
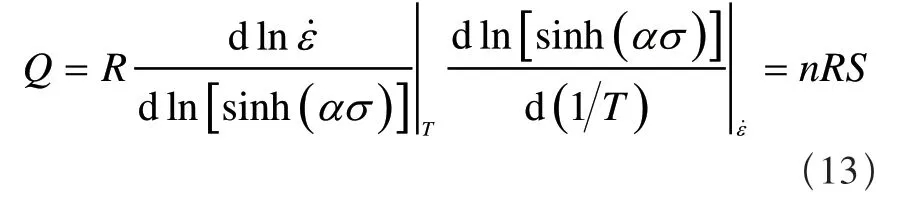
式中n——ln-ln[sinh（ασ）] 直线斜率；

S——ln[sinh（ασ）]-1000/T直线斜率；

由式（13）可知，在Q与变形温度无关的情况下，ln[sinh（ασ）]-1000/T和ln-ln[sinh（ασ）]呈线性关系，令n为直线ln-ln[sinh（ασ）]的斜率，即S为直线ln[sinh（ασ）]-1000/T的斜率。为了获取更高的精度，取ε=0.3处的流变应力及对应的温度，再次建立对应的ln-ln[sinh（ασ）]图（见图8）。通过最小二乘法对图8进行线性回归计算，结果见表4，计算得到n=2.426，再将n值代入到α=β/n得到一个重新调整的α2值，即α2=0.0469。

图8 ln -ln[sinh（ασ）]曲线 （斜率为n）

将最终得到的α2值重新代入到式（13），并绘制新的ln[sinh（ασ）]-1000/T曲线（见图9），对图9

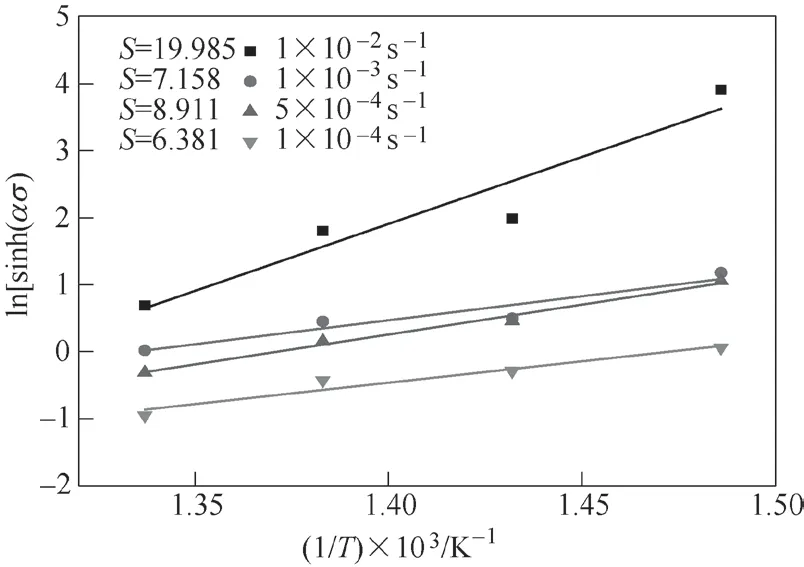
图9 ln[sinh（ασ）]-1000/T曲线（斜率为S）

中4条直线斜率的平均值进行最小二乘法线性回归得到S值。由表4可知，S=10.609。

表4 ln =A+B ln[sinh（ασ）] （斜率为n）和ln[sinh（ασ）]=A+B（1000/T） （斜率为S）的一元线性回归结果（ε=0.3）

表4 ln =A+B ln[sinh（ασ）] （斜率为n）和ln[sinh（ασ）]=A+B（1000/T） （斜率为S）的一元线性回归结果（ε=0.3）

T/℃B（n）B（n）相关系数B（n）B（S）平均值B（S）B（S）相关系数平均值400 2.152 0.968 2.426 19.985 0.874 425 2.610 0.969 7.158 0.871 450 2.410 0.987 8.911 0.983 475 2.532 0.990 6.381 0.916 10.609

根据式（13），代入计算结果见表5，最终确定粗晶5083铝合金热变形过程中Q=213.992kJ/mol，远高于大部分纯铝的自扩散激活能Q（142kJ/mol）值。材料的组织在变形过程中产生了复杂的变化，而且多种机制共同作用，因此激活能就呈现出不同的值。在上述微观组织分析中与此处激活能计算值可相互对应，激活能越小，材料发生塑性变形的抵抗能力越弱。由表5可知，温度为450℃、应变速率为1×10-2s-1时，激活能最大（Q=400.479kJ/mol）且微观组织变化不均。当应变速率为1×10-3s-1时，材料伸长率最大，且由图4可知，被拉长的晶粒最均匀，动态再结晶明显，因此激活能（Q=143.439kJ/mol）也大大下降。同理，对应图4，应变速率为5×10-4s-1时，动态再结晶生成的细小晶粒已经开始长大，故伸长率下降，激活能（Q=178.567kJ/mol）升高。

表5 各区间内粗晶5083铝合金的变形激活能Q值 （双曲正弦函数型）

4 结束语

1）粗晶5083铝合金的应力-应变曲线根据变形条件的变化呈现出一致的变化趋势，应力在变形初期随应变的增大而快速升高，在达到峰值后应力逐渐趋于稳定。当应变速率相同时，材料在相同应变下的应力随变形温度的增加而明显降低。当变形温度相同时，随着应变速率的增加，材料的应力水平升高。

2）粗晶5083铝合金通过双曲正弦函数方程计算得到的热变形的平均激活能Q=213.992kJ/mol，大于纯铝的自扩散激活能Q（142kJ/mol），激活能的变化趋势与组织变化趋势一致，随着组织均匀变化，激活能变小，塑性变化过程中发生的动态再结晶有利于激活能降低。

3）铝合金的超塑性并不局限于晶粒尺寸<10μm的合金，晶粒尺寸较大的合金同样具有良好的超塑性，主要基于变形过程中的动态再结晶，细化了晶粒，促进了晶界滑移，微观组织变化与计算得到的激活能可有效对应。本试验中平均晶粒尺寸87.6μm的粗晶5083铝合金在塑性变形的过程中包含晶界扩散机制和动态再结晶机制。