求解非单调变分不等式的一种二次投影算法*

王霄婷， 龙宪军， 彭再云

（1. 重庆工商大学 数学与统计学院，重庆 400067；2. 重庆交通大学 数学与统计学院，重庆 400074）

引 言

设 H 是具有内积 〈·,·〉和范数 ‖·‖的实 Hilbert 空间， C⊆H 是一个非空闭凸子集， F : H→H 是一个非线性算x∗∈C 子.本文考虑的变分不等式问题是：寻找 ，满足

记问题(1)的解集为 Sol(C,F).

变分不等式作为非线性分析中的重要分支，在交通、运输、博弈论、机器学习和网络规划等领域都有着广泛的应用[1-10].投影算法是求解变分不等式问题的一种主要方法，最早的投影算法由Goldstein[11]提出，在F是强单调且 Lipschitz连续的条件下，Goldstein证明了算法的收敛性.由于F的强单调性，算法的使用受到了限制.1976年，Korpelevich[12]提出了外梯度算法，在单调和 Lipschitz连续的假设下证明了算法的收敛性.1999年，Solodov和Svaiter[13]在有限维空间中提出了一种新的二次投影算法，在非单调和连续的假设下证明了算法的收敛性.在 Hilbert空间中，Vuong和Shehu[14]提出了Halpern型二次投影算法，在伪单调和一致连续的假设下证明了算法的收敛性.最近，Reich等[15]通过构造一类新的严格分离当前迭代和变分不等式解集的超平面，对文献[14]中的算法进行改进，提出了两种新的算法，并在伪单调和一致连续的假设下证明了其算法的收敛性.

本文受文献[13-15]的启发，提出了一种新的二次投影算法.在没有单调性的假设下，证明了算法强收敛到变分不等式问题的解.

1 预 备 知 识

设 H 是实 Hilbert 空间， C⊆H 是非空闭凸子集.记 xn→x 为 {xn}强收敛于x， xn⇀x 为 {xn}弱收敛于x.对任意的u,v∈H,α∈(0,1)，有

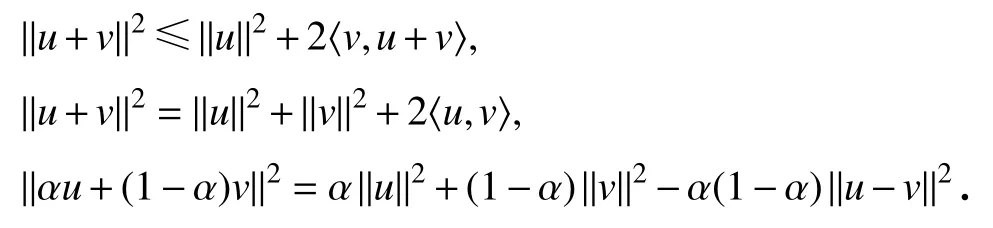
任给x∈H，则存在C中唯一的最近点PC(x)满足

‖x-PC(x)‖≤‖x-y‖, ∀y∈C,

PC叫做H到C 上的投影，易知 PC为H到C 上的非扩张映射.

定义1 设 F : H→H 是一映射.

(ⅰ) 称F是伪单调的，如果 〈F(x),y-x〉≥0⇒〈F(y),y-x〉≥0,∀x,y∈H.

(ⅱ) 称F是 Lipschitz连 续的，如果 ‖F(x)-F(y)‖≤L‖x-y‖,∀x,y∈H ，这里L为 Lipschitz常 数且 L＞0.

引理1[2]设C ⊆H 是非空闭凸子集，对任意的 x∈H，有

(ⅰ) 〈 x-y,PC(x)-PC(y)〉≥‖PCx-PCy‖2,∀y∈H.

(ⅱ) ‖ PC(x)-y‖2≤‖x-y‖2-‖x-PC(x)‖2,∀y∈C.

引理2[2]设C ⊆H 是非空闭凸子集.给定 x∈H,z∈C，则 z = PC(x)⇔〈x-z,z-y〉≥0,∀y∈C.

引理3[3]设 C⊆H 是非空闭凸子集， h(x)是H上的实值函数，定义集合 K := {x∈C : h(x)≤0}.如果K非空且 h(x)在C 上是 Lipschitz连续的，则

dist(x,K)≥θ-1max{h(x),0}, ∀x∈C,

其中 dist(x,K)表示x到K的距离，θ为 Lipschitz常 数，且 θ＞0.

引理4[4]设 {an}是非负实数序列，满足以下关系：

an+1≤(1-ηn)an+ηnsn.

若{ηn}，{sn}满足：(ⅰ) { ηn}⊂(0,1),; (ⅱ) l imsupn→∞sn≤0，则 limn→∞an= 0.

引理5[2]x∗∈Vol(C,F)，当且仅当 x∗= PC(x∗-λF(x∗)).

本文假设

(C1)映射 F : H→H 在C 中的有界集上是一致连续的.

(C2)变分不等式解集 Sol(C,F)非空.

(C3)对于 x∗∈Sol(C,F)都有

(C4)f :C→C 是一个压缩映射且压缩系数为 ρ∈[0,1).

(C5)序列 {αn}⊆(0,1)，且满足

2 算法与收敛性证明

本文提出如下算法：

算法1选取 σ∈(0,1)， γ∈(0,1)， λ∈选取初始点x1∈C.

步骤1计算

如果r(xn) := xn-zn= 0，则算法停止，xn是变分不等式的解.否则，转到步骤2.

步骤2计算

其中 τn:=γmn，mn是满足下式的最小非负整数m：

步骤3计算

其中

令n = n+1，并回到步骤1.

注1 (ⅰ) 显然由算法1产生的序列{xn},{yn},{zn}都属于C.

(ⅱ) 假设 (C1)~ (C4)成立，由引理5可知，若 r(xn) = 0，则 xn是变分不等式的解，算法停止.否则根据映射F在C 上的一致连续性以及引理1，可得

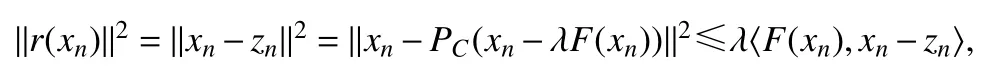
即〈F(xn),r(xn)〉≥λ-1‖r(xn)‖2λ∈.又因为从而

(ⅲ) 如果F是伪单调的，则式(2)成立，反之则不成立，具体例子可参见文献[16]中的例3.1.由此说明假设 (C3)比伪单调性更弱.

引理6假设 (C1) ~ ( C4)成立，且函数 hn(x)由式(5)定义.(ⅰ) 如果 r(xn)≠0，则 hn(xn)＞0；(ⅱ) 如果x∗∈Sol(C,F)，则 hn(x∗)≤0.

证明由 hn(x)定义知 hn(xn) =若r(xn)≠0，有 hn(xn)＞0.另一方面，

结合式(2)和(4)可得

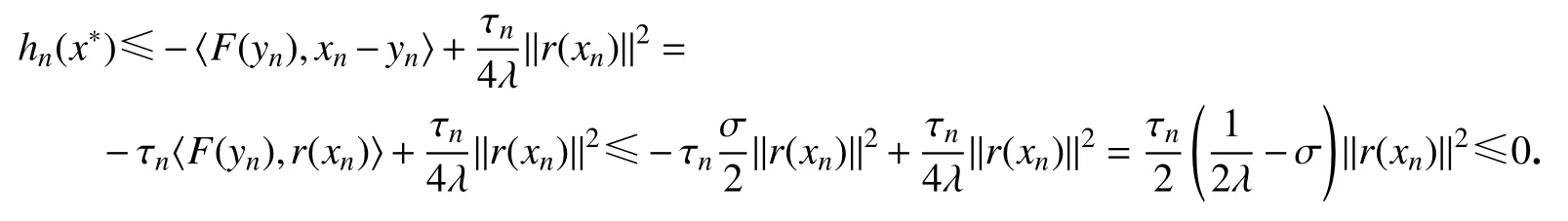
从而引理6得证.

引理7 假设 (C1) ~ ( C5)成立，则由算法1产生的序列 {xn}有界.

证明设p∈Sol(C,F)，由引理1(ⅱ)可得 ‖PCn(xn)- p‖2≤‖xn- p‖2-‖PCn(xn)-xn‖2.故 ‖PCn(xn)- p‖≤‖xn- p‖.结合 {xn+1}的定义知

这表明 {xn}有界.

引理8假设 (C1) ~ ( C4)成立， {xn}为算法1产生的序列.如果 limn→∞τn‖xn-zn‖2= 0，则 limn→∞‖xn-zn‖= 0.

证明我们考虑以下两种情形.

情形1若 liminfn→∞τn＞0，则 0≤‖r(xn)‖2=从而

因此limsupn→∞‖r(xn)‖= 0，即 limn→∞‖r(xn)‖= limn→∞‖xn-zn‖= 0.

情形2若 liminfn→∞τn= 0.不妨设 limk→∞τnk= 0， limk→∞‖xnk-znk‖= a＞0.令

则

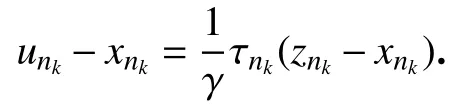
因为 {xnk}有界，所以 {znk}有界，则 {znk-xnk}有界且 limn→∞τnk= 0.由此可得 limn→∞(unk-xnk) = 0.根据线搜索规则(4)和 {unk}的定义可得

上式等价于

令δnk:= xnk-λF(xnk)，则

又因为

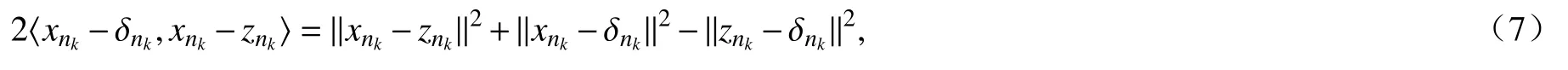
联立式(6)和(7)有

又由F的一致连续性可得 limk→∞‖F(unk)-F(xnk)‖= 0.所以当 k→∞时不等式(8)右边会趋近于(σλ-1)a2＜0，从而有

对于 ϵ= -(σλ-1)a2/2＞0，存在 N∈N，当 n≥N时有

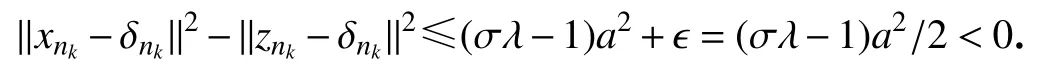
故‖xnk-δnk‖＜‖znk-δnk‖，这与{zn}的定义矛盾.因此 limn→∞‖xn-zn‖= 0.证毕.

定理1 假设(C1)~ ( C5)成立，则由算法1产生的序列 {xn}强收敛于 p∈Sol(C,F)，这里 p := PSol(C,F)°f(p).

证明先证‖PCn(xn)-xn‖2≤‖xn- p‖2-‖xn+1- p‖2+2αn〈f(xn)- p,xn+1- p〉.事实上

由引理1(ⅱ)得

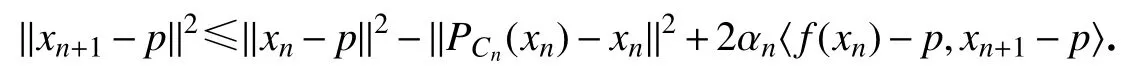
由此可得

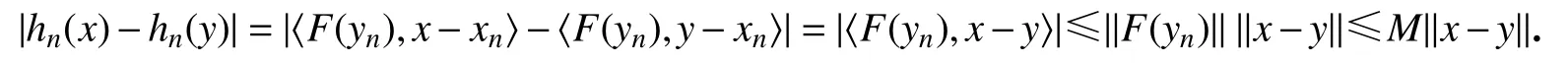
这表明hn(x)是 Lipschitz连 续的，且 Lipschitz常数为M.由引理1、3和6可得

结合{xn+1}的定义知

所以

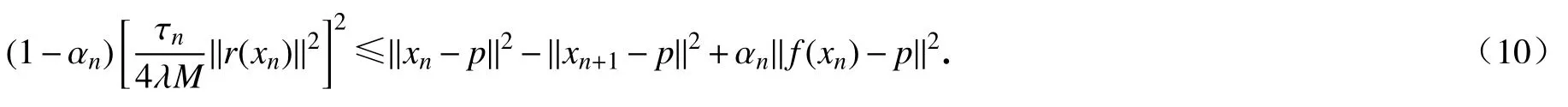
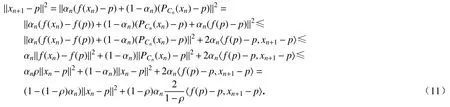
下面分两种情形进行讨论.

情形3若存在正整数 N ，当 n≥N 时有 ‖xn+1- p‖2≤‖xn- p‖2，这表明 limn→∞‖xn- p‖2存在.由式(10)可得，所以

由引理8知

又因为 {xn}有界，所以对 {xn}的任一聚点z都 存在子列 {xnk}，有 limk→∞xnk= z .结合 PC和F的一致连续性可得

故r(z) = 0.又由引理5得 z∈Sol(C,F).另一方面

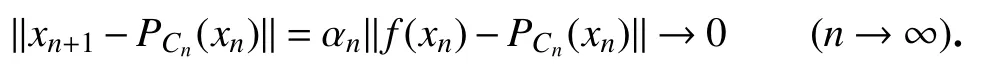
通过式(9)可得limn→∞‖PCn(xn)-xn‖= 0.因此

结合引理2及p := PSol(C,F)°f(p)有

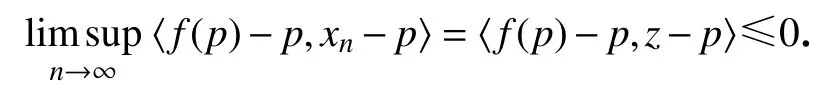
所以有

则依据式(11)和引理4有xn→p(n→∞).

情形4假设不存在 n0∈N 使得是单调递减序列.令 Γn=‖xn- p‖2且有映射 t : N→N 满足对所有的 n≥n0(n0足够大)都有

即 t(n)是1,2,···,n 中使得 Γk为递增序列的最大值k .显然t 是一个非递减序列，且满足 limn→∞t(n) =∞，以及

由Cauchy-Schwarz不等式以及式(9)可得

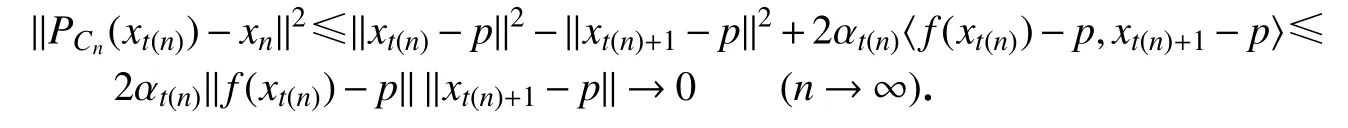
由式(10)可得

类似于情形3的证明可得

以及

由式(11)可得

因此limsupn→∞‖xt(n)+1- p‖2≤0

结合式(12)有 ，即

接下来，我们证明当n≥n0时(n0足够大)，有 0≤Γn≤Γt(n)+1.不难发现，当 n≥n0时有 t(n)≤n.考虑三种情况：当 t(n) = n 和 t(n) = n-1时，显然有 Γn≤Γt(n)+1.现考虑 t(n)＜n-1.对任意的正整数 n≥n0，由 t(n)的定义知，有Γj≥Γj+1，当 t(n)+1≤j≤n-1时，得到 Γt(n)+1≥Γt(n)+2≥···≥Γn-1≥Γn，因此当n足 够大时， 0≤Γn≤Γt(n)+1恒成立.联立式(13)可知 limn→∞Γn= 0，即算法1迭代产生的序列xn强收敛于p.

3 数 值 实 验

在本节中给出了算法1在一个简单例子中的计算机检验结果，并与文献[14]中算法3.3及文献[15]中算法4进行比较.本文中所有代码都是在MATLAB R2020a和Windows10系统下运行的.计算机基本参数为Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz.此外，用“iter”表示算法迭代次数，“CPU time”表示程序运算的时间，单位为s.参数选取如下：

例1设映射 F : Rm→Rm满足 F(x) = Mx+q ，这里 q∈Rm且 M = NNT+S+ D，其中为反对称矩阵，D为 对角矩阵且对角元素非负.取可行集

容易得到F是一个单调且Lipschitz连续的映射，其中Lipschitz常 数L=‖M‖.对于q = 0，相应的变分不等式的唯一解是{0}.

在本文的实验中，矩阵N,S中所有元素都在区间(-2,2)上随机产生，矩阵D中的对角元素在(0,1)上随机产生.此外，设置所有算法中最大迭代次数为，停机条件为，其中εerr为给定的误差界.在此情况下，我们对比了不同的维数、不同的初始点以及不同的误差界εerr三种算法的数值效果，具体如表1 ~ 3所示.通过观察表中的数据可以发现，算法1在三个维度上的数值效果优势非常明显.

表 1 εerr= 10-4时不同算法关于维数的比较Table 1 For εerr= 10-4, comparison of different algorithms about dimensions

表 2 εerr= 10-4时不同算法关于初始点的比较Table 2 For εerr= 10-4, comparison of different algorithms about the initial point

表 3 m = 100时不同算法关于允许误差的比较Table 3 For m = 100, comparison of different algorithms about allowable errors

4 结论与展望

本文利用线搜索方法，提出了一种新的求解非单调变分不等式的二次投影算法，在映射是一致连续的条件下证明了算法的收敛性.本文所得结果改进了文献[14-15]中对应的结果.数值实验展示了本文算法的优势.本文主要对变分不等式问题的算法进行了研究，如何将所得结果应用于图像处理以及网络规划等问题中，有待进一步研究.