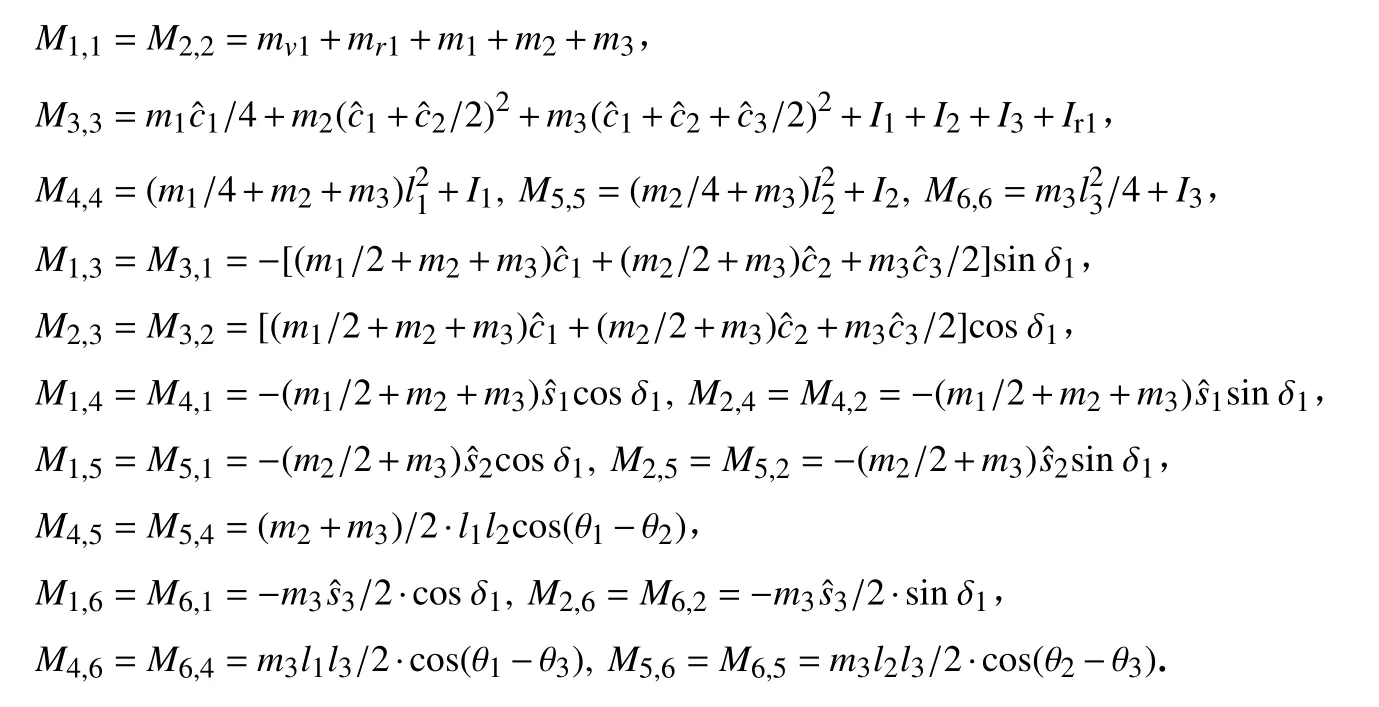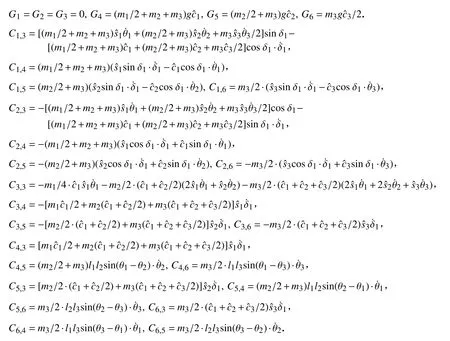双移动机械臂空间协作动力学建模研究*

董方方， 喻 斌， 赵晓敏， 陈 珊

（1. 合肥工业大学 机械工程学院，合肥 230009；2. 安徽省智能数控技术及装备工程实验室，合肥 230009；3. 合肥工业大学 汽车与交通工程学院，合肥 230009）

引 言

移动机械臂的多机协作系统可广泛应用于各种不同场合，如用于风电叶片、火箭壳体、高铁车厢等大尺寸零部件表面的抛磨加工、焊接，以及低刚度、低稳定性零件的搬运、装配等工作.双臂空间协作是多机协作中的典型案例，双臂相比于单臂，具有灵活、高效、相对低成本、高可靠性等诸多优点[1]，能够更好地模仿人类手臂的工作情况.Yan等[2]针对双机协作与单臂作业的差别与优势、协作机械臂的工作环境与资源冲突等诸多问题进行了具体的分析调研.对于需要大范围移动工作的情况，移动机械臂相比于传统的三坐标机械臂，占地面积更小，也更加灵活[3]，20世纪80年代兴起的同步定位与建图技术，使得移动机器人在陌生环境中的适应性得到了极大提升[4].

协作机械臂的建模与控制问题受到了众多研究者的青睐，目前动力学建模常用的方法一般为Lagrange法[5]与Newton-Euler法[6]，此外还有基于Lagrange乘子法的Lie群方法[7]、Kane方法[8]等.Jorge等[9]提出了一种通过Lagrange法建立起单臂作业的动力学模型，再引入双臂协作搬运时关节变量的耦合约束，建立了双机协作搬运机械臂动力学模型的方法.Parra-Vega等[10]针对受约束协作多指抓取机器人，通过Lagrange法，建立了其摩擦模型与动力学模型.Flixeder等[11]针对协作搬运易形变材料的问题，分别针对易形变材料与协作机械臂两部分进行了研究并建立了交互模型.章定国[12]在计算多杆机器人的动力学模型时采用将Lagrange方程与齐次变换矩阵相结合的方式，通过递推策略求得了结果.郭益深等[13]结合Lagrange法与动量守恒理论，建立了双臂空间机器人的模型.Reza等[14]应用多个力传感器，提出了一种针对未知搬运物体的质心估测方法，将未知搬运物体固定在三个虚拟连杆上，并将连杆视作机械臂的一部分进行建模.

移动机械臂空间协作系统具有诸多优势，但由于其存在复杂的耦合关系，使得应用Lagrange法或Newton-Euler法直接进行动力学建模时的计算极为繁琐，应用Lagrange乘子法虽然计算结果的形式相对简洁，但建模思路抽象，且需要引入新的Lagrange乘子.Udwadia与Kalaba[15-16]提出了一种全新的观点，称为Udwadia-Kalaba（U-K）方法.他们将系统分割为若干子系统并建立动力学模型，通过U-K方程引入各子系统的固有几何约束，无需引入辅助变量即可构建复杂系统整体动力学方程，从而达到简化计算的目的.

已经有许多研究者基于U-K方法进行了探索.韩江等[17]以平面2自由度冗余驱动并联机器人作为研究对象，将系统分解为三个无约束开链子系统，建立无约束子系统模型后再引入支链末端位置约束，利用U-K方法求取约束力建立起其动力学方程.Huang等[18]针对并联机械臂，应用U-K方法构建了其正逆动力学方程.韩江等[19]提出了一种基于U-K方法的协作机械臂轨迹跟踪控制.刘佳等[20]和Zhen[21]针对双机平面协作搬运问题，将系统从一条机械臂基座处断开，形成虚拟5自由度机械臂进行建模，再利用U-K方法引入基座约束建立了动力学模型.

目前基于U-K方法，针对协作双臂搬运系统建模问题，大多是基于平面动力学系统进行研究.本文结合Lagrange方法与U-K方法，建立了双移动机械臂空间协作搬运的动力学模型.由于本文的研究对象中存在移动平台，且平台底面必须始终与地面平行，故针对本文的研究对象，在建模过程中若直接采用文献[20-21]的方法，将机械臂末端连杆与旋转关节视作断开进行建模，虽然形成5自由度虚拟机械臂的方式同样易于理解，但会导致无法引入断开端基座电机转角与断开端连杆转角的约束，造成约束缺失，且非线性耦合严重，最终表达式极其繁琐.故本文提出了一种基于对称思路的建模方法，该方法将负载中心处视作断开，以将整体系统分割成两个子系统，两个子系统拥有高度对称的动力学模型特征与约束关系，因此只需要利用Lagrange方法对其中一个子系统进行建模，即可得出两个无约束子系统的动力学模型，再将固有几何约束与期望轨迹以约束形式给出，即可通过U-K方程建立起整体模型.该方法的对称建模思路，使得建立子系统动力学模型与约束方程时只需要考虑某一子系统即可得出整体方程，简化了建模所需计算量，同时也避免了约束信息缺失的问题，且该方法探索了U-K方法在三维工作空间协作机械臂上的应用，将U-K方法针对双臂协作机器人的应用推广到了空间协作的情况.

1 应用U-K方法的一般步骤

U-K方法在稳定无约束子系统的动力学方程的基础上，向子系统施加约束力，子系统同时受到平衡力与约束力的作用，使其稳定且始终满足给定的约束条件.根据U-K理论的一般应用方法[22]，建立具有n个自由度的动力学系统模型的步骤如下：

（Ⅰ）建立无约束系统动力学方程：

式中，t为时间，M 为系统的 n×n维 惯性矩阵，q为广义坐标，Q为施加在系统上的广义力.

式中，A为 m×n维 矩阵，b为 m维 向量.

（Ⅲ）计算约束力，受约束系统动力学方程为

式中，Qc为约束力，上标“＋”表示矩阵的Moore-Penrose广义逆矩阵.

对于一般的机械系统，现提出如下假设.

假设1对于任意 q∈Rn，总有 |M(q)|＞0[23].

假设2对于任意 q∈Rn，矩阵的秩 rank(A)≥1.

假设3对于任意初始条件 q∈Rn均满足约束方程，且约束连续.

2 双移动机械臂空间协作搬运建模

单个移动机械臂由四自由度机械臂与移动平台构成，移动平台使用全向轮或Mecanum轮，可实现平面全向移动，机械臂拥有四个旋转关节，如图1所示.

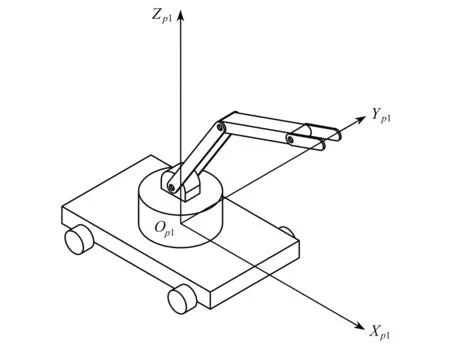
图 1 移动机械臂示意图Fig. 1 The schematic of the mobile manipulator

建立如图1、2所示的空间直角坐标系.以旋转关节 mr1与 mr2下表面圆心处建立坐标系 Op1Xp1Yp1Zp1与Op2Xp2Yp2Zp2， Zp1与 Zp2轴垂直于移动平台上表面向上， Xp1与 Xp2轴平行于移动平台上表面指向平台前端（如图2所示），并依据右手定则确定 Yp1与 Yp2轴.以初始位置处的机器人坐标系确定世界坐标系 OwXwYwZw.

图2中部件 m3与 m6为机械臂末端负载，可简化为连杆，并假想该连杆中心处分离进行建模，图中变量Δxi和 Δyi分别表示平台i 在 Xw和 Yw方向的位移，变量δi和θi分别表示旋转关节i 和连杆i 的转角，变量 Fxi和 Fyi分别表示平台i 在 Xw和 Yw方向受到的驱动力，变量τi和ui分别表示旋转关节i 和连杆i 的扭矩，物理量 mi，Ii，li分别表示部件i 的质量、转动惯量和长度，Δz表示两移动平台高度差.

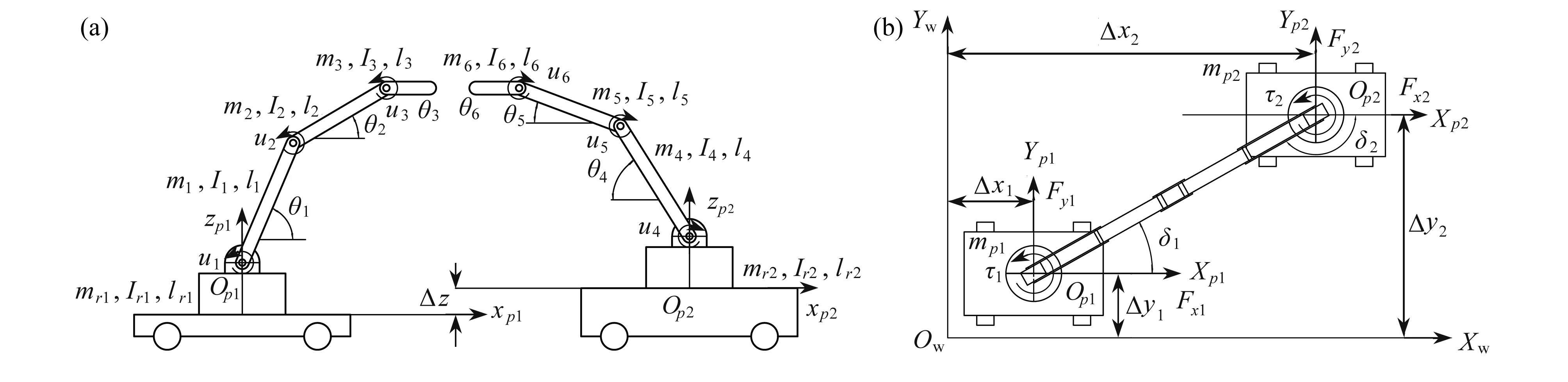
图 2 双移动机械臂空间协作系统示意图： (a) 主视图；(b) 俯视图Fig. 2 The schematic of dual-system cooperative handling mobile manipulators: (a) the main view; (b) the vertical view

2.1 无约束子系统动力学方程的建立

在此动力学系统中，每个移动机械臂具有6个自由度，包含了与移动平台相连接的关节转动.由于移动平台采用全向轮或Mecanum轮，在实际搬运过程中给定运动轨迹后，移动平台的转动并不会对搬运过程造成影响.为简化计算，本文暂不考虑移动平台的整体转动.在不考虑约束条件下，该动力学系统共有12个自由度，需要12个状态变量进行描述，选择广义坐标 q = [Δx1,Δy1,δ1,θ1,θ2,θ3,Δx2,Δy2,δ2,θ4,θ5,θ6]T，对该动力学系统施加外力 τ= [Fx1, Fy1,τ1, u1, u2, u3, Fx2, Fy2,τ2, u4, u5, u6]T.

与文献[18-19]中末端关节与连杆处断开方式相比，选择负载中心处断开的方式具有如下优势：第一，两子系统动力学特性相同，故只需要针对某一子系统进行建模，即只需建立起无约束6自由度子系统模型，形式相对简洁.若在本文研究对象中采用文献[18-19]所用方法，虽然方法与形式上同样易于理解，但需要建立起一个3自由度模型（移动平台 + 旋转关节）与一个8自由度模型（移动平台 + 6自由度虚拟机械臂）.其中，8自由度模型计算量大且形式极其繁琐.第二，若文献[18-19]的方法应用在本文的研究对象上，会导致难以引入断开端基座电机转角与断开端连杆转角的约束，导致约束缺失.选择负载中心处断开则无需考虑该约束.

采用Lagrange方法，对图2中左半子系统进行建模.由文献[24]可知，对有n个自由度的一般系统应用Lagrange方程进行建模，可得到一般形式的动力学模型.其中惯性矩阵 M∈R12×12的计算方式如下：

首先计算各部分速度的Jacobi矩阵，可知

式中，νk和 ωk分别为机构k 质心处的线速度与角速度，和分别为矩阵和的第j 列.

计算得各部件质心处线速度，由式(6)计算可得Jacobi矩阵 Jv，左半子系统矩阵 JvL如下：

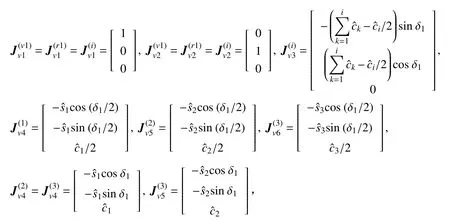
同理，可得到各部件质心处角速度，由式(7)计算可得Jacobi矩阵，左半子系统矩阵如下：

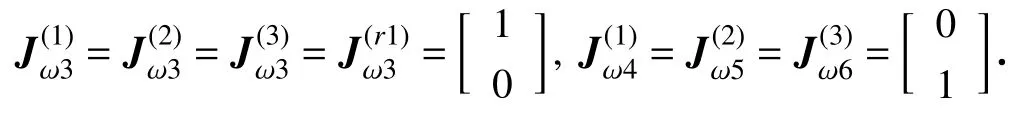
同理，可得矩阵G(q)∈R12的计算方式如下：

式中，Gi为矩阵 G 的第i 个元素，g为 广义坐标下的重力加速度.

机械臂在转动时会受到向心力与Coriolis力，可统一表示为，其中 C∈R12×12.向量是唯一确定的，但矩阵C 并不唯一.可以将矩阵规范为反对称矩阵，以此确定矩阵C[25]，得到矩阵C的计算公式如下：

式中，Cij为矩阵C 的第 (i, j)个元素， Mij为矩阵 M 的第 (i, j)个元素.

由式(5)、(8)、(9)计算可得左半子系统矩阵 ML，GL，CL与右半子系统矩阵 MR， GR， CR. ML，GL，CL的具体计算结果见附录.

至此，可得子系统形式的一般动力学方程：

将其变化为式(1)所示形式，可得

式中

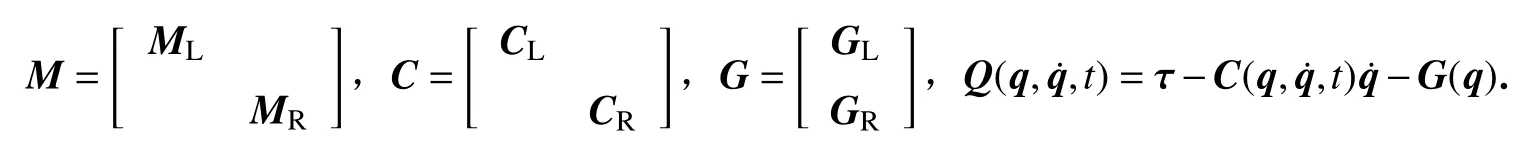
2.2 约束方程的建立

假定机械臂进行水平搬运，假想断开连杆实际为一整体，故假想末端 x,y,z 坐标应重合，且转角 δ1,δ2及θ3,θ6应满足物理结构约束条件.对位置所进行的约束，要求断开处时刻保持位置相同，实际上已经隐含了对速度和加速度的约束（将位置约束求一阶导数即为对速度的约束，求二阶导即为加速度约束），因此无需额外考虑对速度与加速度进行额外的约束.由于采用负载中心处进行断开的方法，因此也无需考虑连杆转角与关节转角之间的约束关系，避免了约束信息缺失.由此，建立以下约束方程组：

显然该约束为完整约束，将约束方程(12)对时间t 求二阶导数，得到

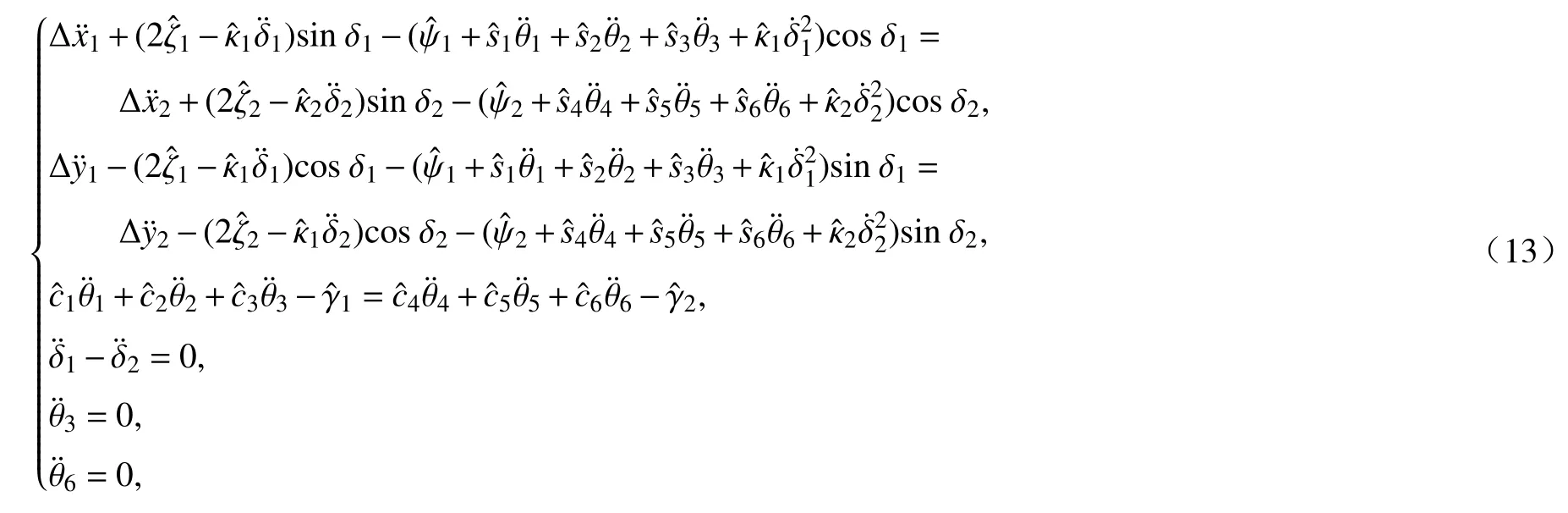
式中

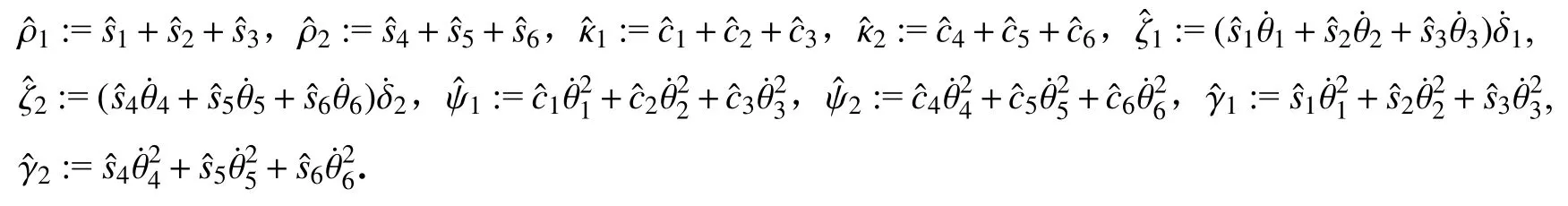
将约束方程二阶导数写成式(2)所示形式，可得

矩阵A与b的具体计算结果如下：

至此已经得到矩阵 M, A,Q与 向量b，根据式(4)计算得约束力 Qc：

求得的约束力 Qc为系统受到约束(12)时产生的力，在无约束子系统的动力学方程(11)的右侧添加求得的约束力，使得两个子系统始终满足约束(12)，从而得到协作系统动力学方程：

从以上建模过程中可以看出，采用U-K方法建模，不需要引入Lagrange乘子或者辅助变量，得到的是约束力的解析解，并且求解过程相对简洁.

3 数值仿真分析

本节将通过仿真软件进行数值仿真，以检验证模型的准确性.为了验证模型的准确性，需要验证两假想断开末端是否始终重合，δ1，δ1及θ3，θ6是否符合约束(12).为此，假想断开连杆左端添加期望轨迹约束：

式中， xi,yi,zi为机械臂末端初始位置的坐标常量.

求二阶导数得

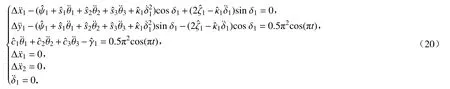
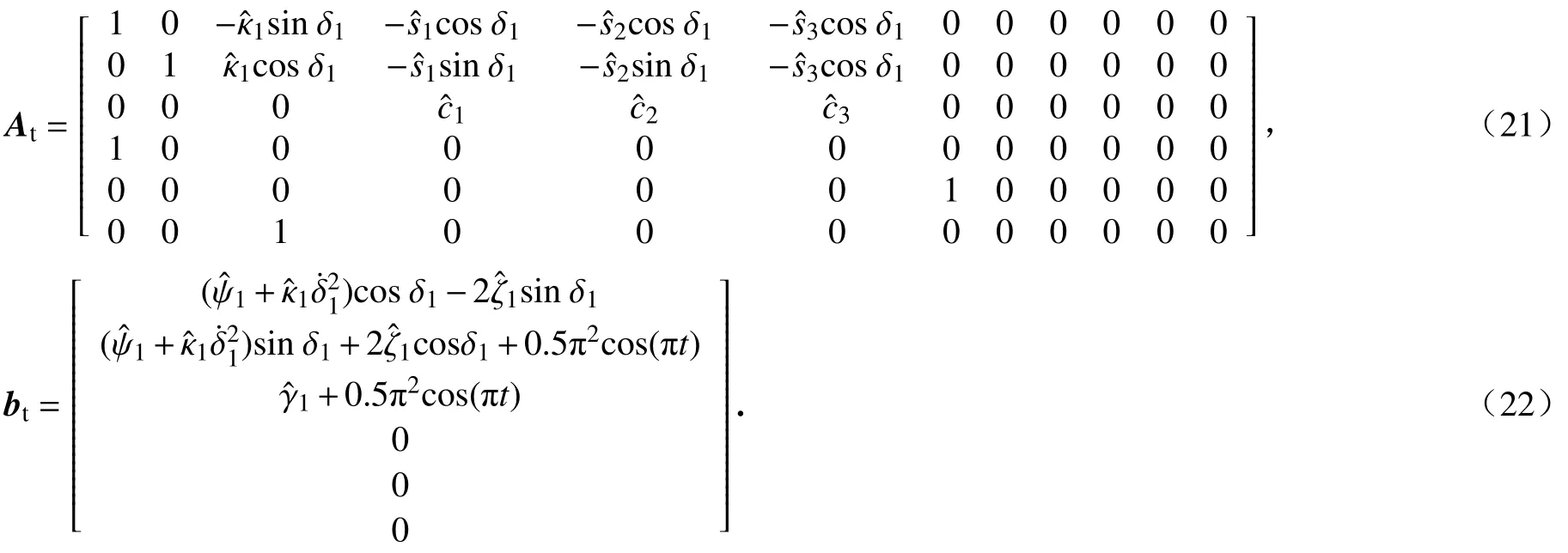
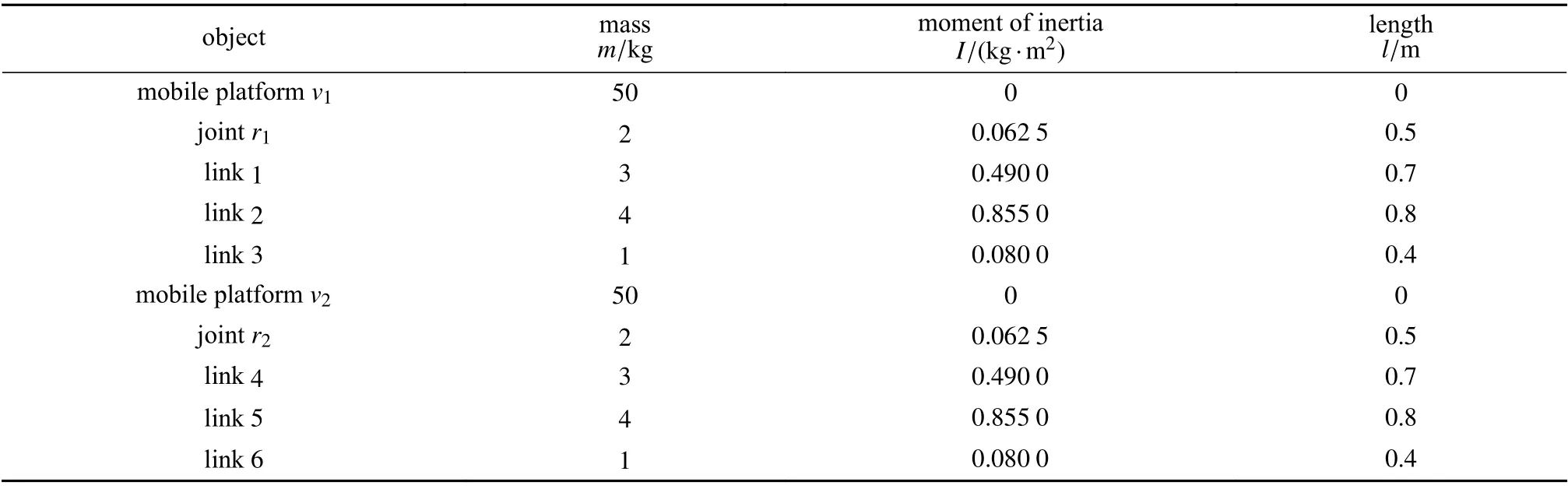
表 1 系统动力学参数表Table 1 Dynamic parameters of system

此外，我们还需要知道系统的初始位置信息与初始速度和加速度信息，且初始状态必须满足约束条件(12)，给定如下初始位置、速度与加速度：取给定任意初值τ，图3 ~ 6为仿真结果.

图 3 断开处轨迹示意图Fig. 3 Trajectories at disconnection points

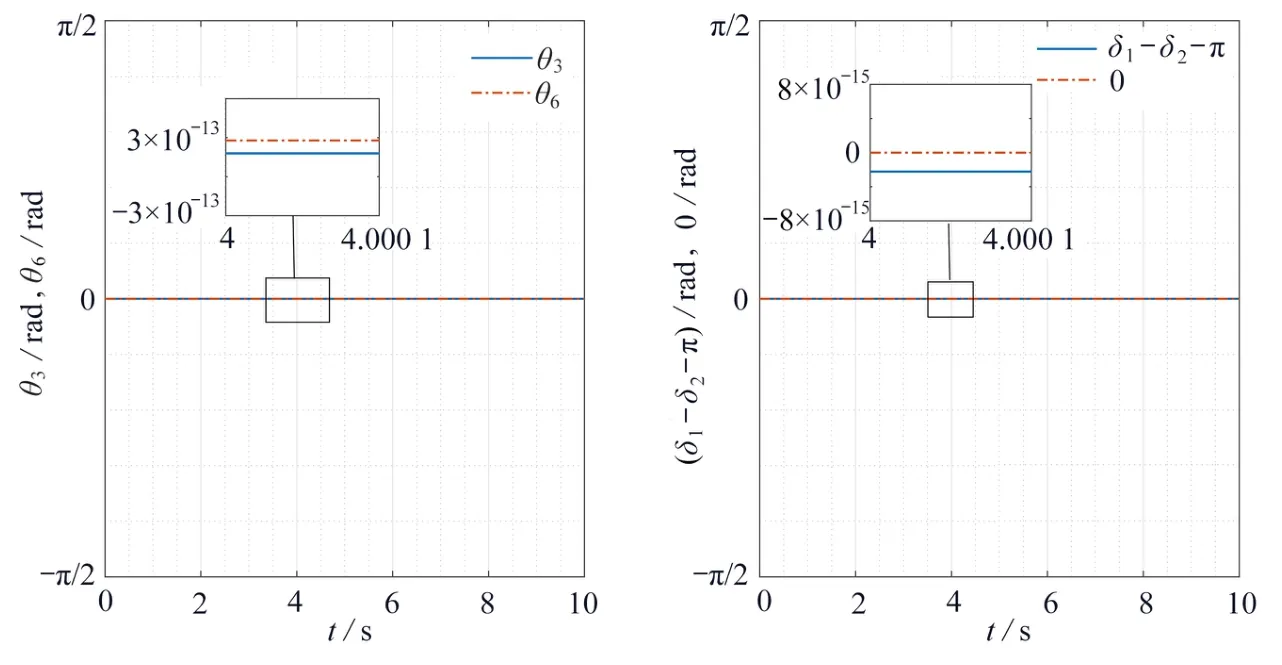
图 4 关节角度约束示意图Fig. 4 Joint angle constraints

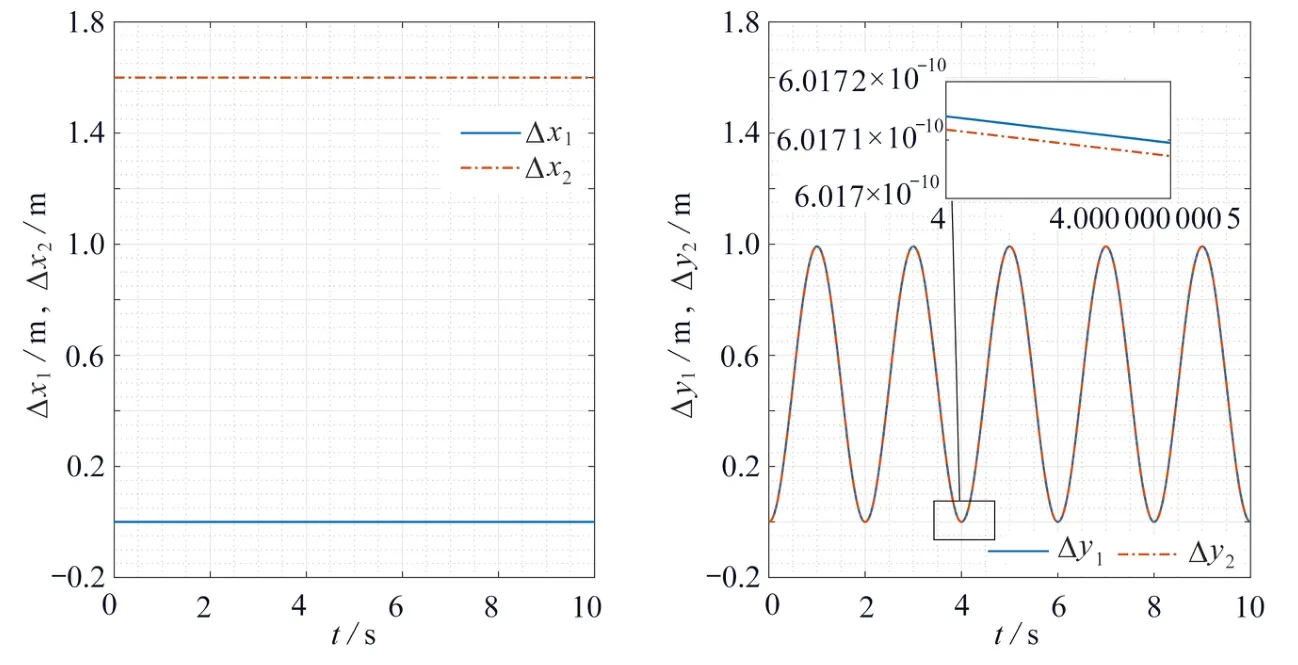
图 5 移动平台位移示意图Fig. 5 Displacements of mobile platforms

图3中x， z方 向误差量级为1 0-13，y方 向误差量级为1 0-15，可视作负载断开处运动时基本重合，x方 向无位移，y， z方向做周期往复运动，满足固有几何约束及给定运动约束.图4中 θ3与 θ6误差量级为1 0-13，δ1与 δ2方向误差量级为1 0-15，可视为满足固有几何约束.移动平台在x方 向保持静止，在y 方向做周期往复运动，满足给定运动约束，机械臂关节转角在满足约束的条件下做周期运动.仿真结果表明该方法构建的空间协作动力学模型准确可用.

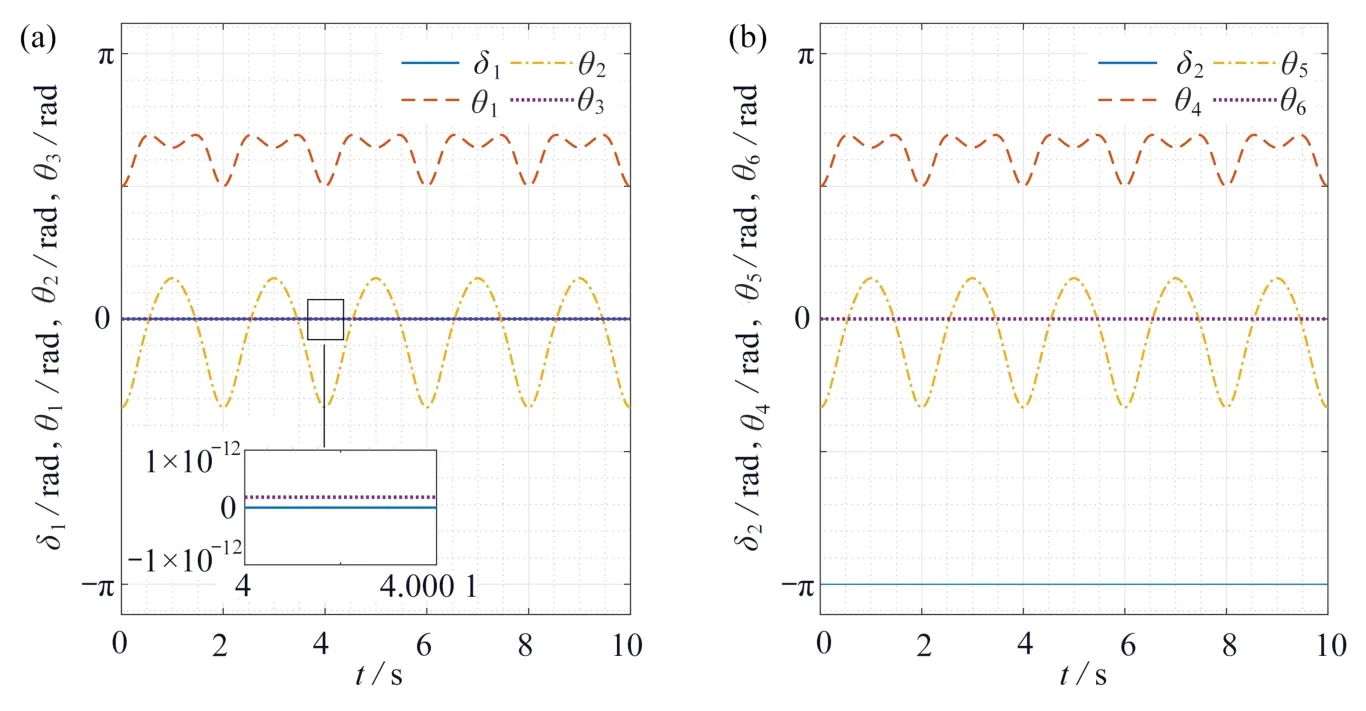
图 6 子系统转角示意图：(a) 左半子系统；(b)右半子系统Fig. 6 Rotation angles of subsystems: (a) the left subsystem; (b) the right subsystem

4 结 论

双移动机械臂空间协作系统存在复杂的约束与非线性耦合，使得直接建立动力学模型极为困难，故本文中提出了一种基于U-K方程对系统建立动力学模型的方法.主要结论如下：

1) 将负载的中心处断开，应用Lagrange方法建立了单个移动机械臂的动力学方程，减轻了系统的耦合现象，解决了引入约束方程时无法对末端电机转角与末端连杆转角加以限制的问题.

2) 给出了将双移动机械臂空间协作的固有几何约束及其二阶导数，应用U-K方程建立了双移动机械臂空间协作系统的动力学模型.该方法思路清晰，无需引入辅助变量，简化了计算量.此外，现有针对双臂协作问题的研究主要是基于平面协作进行的，而本文针对空间协作机械臂开展了应用U-K方法的探索.

3) 对建立的模型进行了数值仿真，对模型添加期望的轨迹约束，给定了符合约束方程的初始条件，仿真显示模型运动轨迹与期望轨迹基本重合，证明了该方法建立动力学模型的可行性.由于该方法未考虑负载与机械臂之间的密度变化，且将连杆质心简单视作连杆中心，因此存在一定的建模误差.后续的研究可以把此类误差统一整合至不确定性中，进一步基于该模型进行控制算法的探索.

附 录