基于分数阶Fourier变换的结构瞬时频率识别*

卢 恋， 任伟新， 王世东

（1. 合肥工业大学 土木与水利工程学院，合肥 230009；2. 深圳大学 滨海城市韧性基础设施教育部重点实验室（筹），广东 深圳 518060）

引 言

工程结构运营时所处的复杂环境荷载和激励，其本质不仅是随机而且是非稳态的.列车通过桥梁发生振动，结构长期运营发生累积损伤导致刚度退化，结构在地震、强风等灾变荷载作用下，在一定程度上表现出较强非线性行为等，均会导致结构特性参数随时间变化，因而，识别结构的时变和非线性参数更符合实际情况，这不仅是工程实际和结构健康监测的重大需求，同时也是工程结构参数识别理论发展的趋势[1].

工程结构的时变参数识别是近年来的一项前沿研究课题，以往基于线性系统和动力响应信号平稳性假定的分析方法，如传统的Fourier变换（FT）是一种全局变换，其频域上不包含时间信息，无法反映信号频率随时间变化的趋势.时频分析方法能同时在时域和频域内分析信号的时频特征，能更好地反映信号的本质特性，是分析非平稳信号的有力工具.其中包括：Hilbert变换（HT）[2-3]、Wigner变换[4]、短时Fourier变换（STFT）[5]、连续小波变换（CWT）[6]、分数阶Fourier变换（FRFT）[7]等.在Hilbert变换中，Feldman[8]提出了一种新的非平稳信号分解公式——Hilbert振动分解方程（HVD），实现了对待测信号进行适当的分解，并使分离出的信号具有良好的Hilbert变换特性.为了研究Wigner变换在实际工程中的适用性，续秀忠等[9]利用Wigner变换和短时Fourier变换两种方法识别时变刚度系统的模态参数，可以得到较为准确的时间和频率分辨率的识别结果.从理论上讲，Wigner变换为非平稳单分量线性调频（FM）信号提供了很好的时频分布，但是在多分量和非线性调频单分量信号的情况下引入了交叉项.为了克服这一缺点，提出了基于Fourier-Bessel级数展开的方法[10].2012年，Chen和Wang[11]提出了一种新的信号分解方法——解析模态分解（AMD），通过对该方法进行扩展，可以提取非平稳信号的振动特征.

在短时Fourier变换中，利用间隔较短的时间窗函数将信号分为平稳的若干小段，并对所有时间间隔进行Fourier变换得到窗内信号的频率成分，随着时间窗函数在信号的时间轴上滑动，最终可以获得信号频率与时间的对应关系.然而，固定形状的窗函数导致了时间和频率分辨率无法同时提高，使得合理选择窗函数和控制窗长度成为短时Fourier变换的关键.廖庆良[12]以一大跨度悬索桥为研究对象，利用试验数据进行了验证，探讨了如何利用短时Fourier变换提高结构参数识别的准确度.连续小波变换是对短时Fourier变换的进一步改进，其本质上是一种基于可调窗口的信号分析工具.与单一分析窗的短时Fourier变换相比，连续小波变换在高频处使用短窗，低频处使用高窗，有效克服了短时Fourier变换的分辨率限制.研究者提出了很多方法来提高小波脊线的时频分辨率，便于识别结构的时变参数[13-14].时变结构的瞬时频率的识别与小波脊线有直接关系，研究者提出了许多方法以获取清晰的小波脊线.王超和任伟新等[15-16]基于复Morlet小波，利用小波系数模极大值方法提取小波脊线，从而识别出时变结构的瞬时频率.刘景良和任伟新等[17]通过最大坡度法识别出时变结构的瞬时频率，其识别精度高于小波系数模极大值方法，并通过数值模拟和试验证明了该方法对瞬时频率提取的正确性.

从以传统Fourier变换为基础的时频分析方法发展历程可知，小波变换改进了短时Fourier变换的分辨率问题，但在信号处理过程中也面临着基函数合理选择的难题.与此同时，分数阶Fourier变换同样作为传统Fourier变换的推广，相比较于小波变换的双变量，仅有单一变量的分数阶Fourier变换引起了学者们的关注，并且分数阶Fourier变换的核函数为chirp函数，避免了类似小波变换在运用过程中基函数选取的问题.分数阶Fourier变换这一概念最早由Wiener在1929年提出，国内陶然、邓兵等[18-19]对分数阶Fourier变换进行了系列研究.分数阶Fourier变换是由Fourier变换推广而来的一类广义线性变换，它可以被认为是n次的Fourier变换，n不需要是整数.因此，可以把一个函数变换到时间和频率之间的任意中间域，为分数阶Fourier域（FRFD），其同时反映了信号在时域和频域的信息.与常用二次型时频分布不同的是，用单一分量（旋转参数α）来表示时频信息[20]，没有交叉项困扰，在信号分析领域有更强的实用性.

分数阶Fourier变换作为一种新型的信号处理工具，其发展是建立在Fourier变换与短时Fourier变换的基础上，所以其原理有诸多相似性.本文首先从理论分析出发，考虑到连续分数阶Fourier变换的采样型离散分数阶Fourier变换与快速Fourier变换的计算效率相同，充分利用了Fourier变换计算效率高的优势，接着借鉴改变短时Fourier变换窗函数的思路，由分数阶Fourier变换定义式推导出一般信号的频率与分数阶Fourier变换单一变量α的关系式，得到非平稳信号瞬时频率的理论表达式，实现一般时变信号的时频分析，从而达到时变结构瞬时频率的识别的目的，通过非线性调频信号和时变系统数值模拟算例验证方法的可行性和有效性.

1 分数阶Fourier变换基本特性

1.1 分数阶Fourier变换

相应的逆变换为

信号x(t)的Fourier变换及对应的逆变换，使用算子符号的表示如下：

分数阶Fourier变换作为Fourier变换的推广，在时频平面中，分数阶Fourier变换实际上可以被视为坐标轴的逆时针旋转而得到分数阶Fourier域中的表示，如图1所示，等量关系为

式中u为 分数阶Fourier轴，可以看出，传统的Fourier变换可视为当旋转角度为时的分数阶Fourier变换.信号x(t)的分数阶Fourier变换的定义为

Xp(u)的逆变换为

式（5）中的角度α仅在三角函数中出现，因此只考虑范围 α∈(-π,π]（p ∈(-2,2]）.当 α= 0时， X0(u) = x(t)，为原信号；当时， X1(u) =为传统Fourier变换；当时， X-1(u)为信号 x(t)的逆Fourier变换.连续分数阶Fourier变换的一些重要属性如下[21]：

② 酉性：(Fp)-1= (Fp)H；

③ 阶数、叠加性： Fp1Fp2= Fp1+p2.

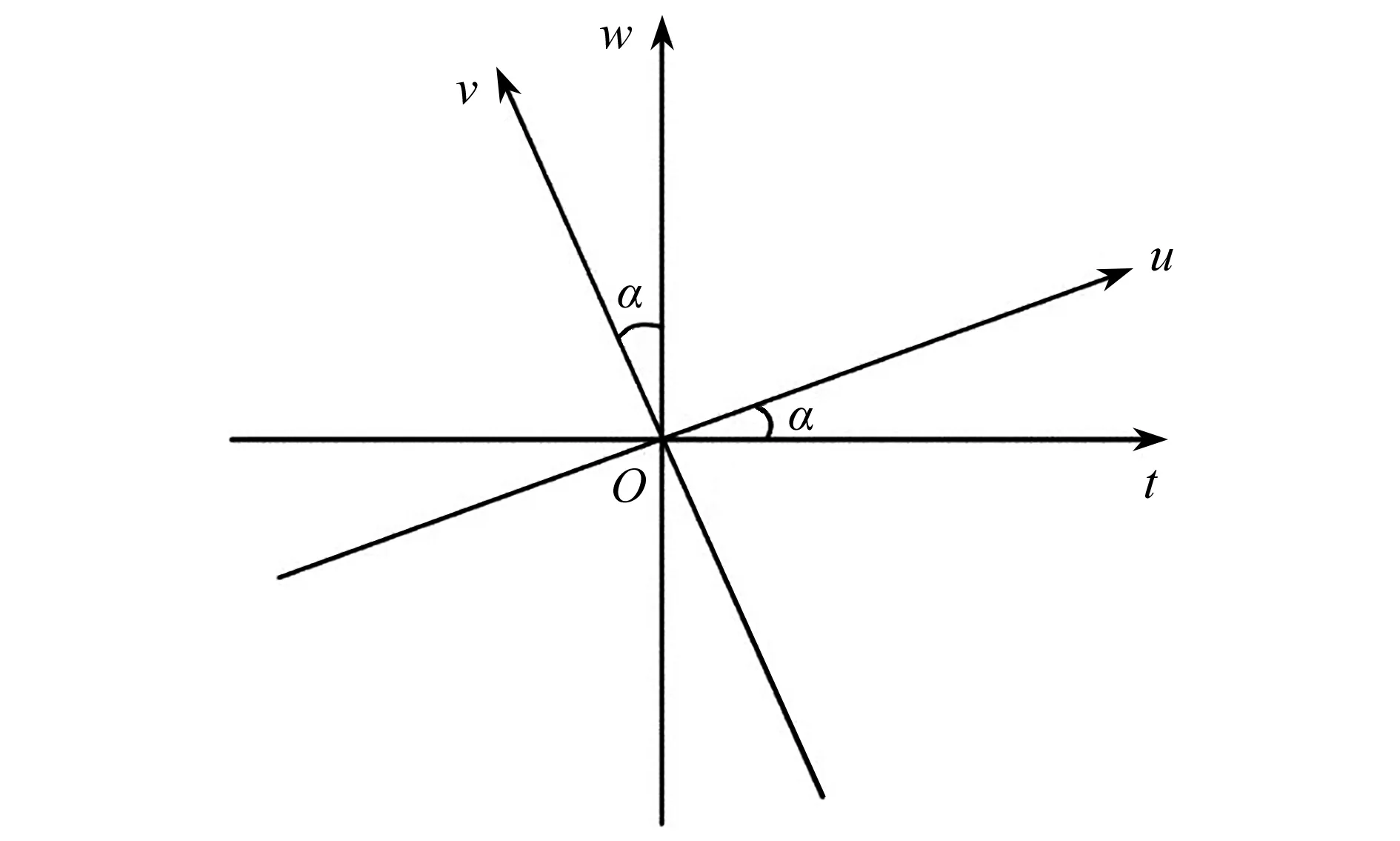
图 1 时频面旋转Fig. 1 Rotation of the time-frequency plane

1.2 离散分数阶Fourier变换（DFRFT）

针对数字信号，DFRFT目前主要有采样型、线型加权型以及特征分解型三种形式.其中以采样型DFRFT的应用最为广泛，该算法由Ozaktas提出，与快速Fourier变换相比，其计算复杂度同为O(NlgN).在数字信号处理系统中，所使用的信号是从模拟信号采样的数字信号，即离散信号，为了实现采样型DFRFT的实际工程应用，需要将离散信号量纲归一化处理[22]，其过程如下.

假定原始信号的时域表示限定在区间 [-Δt/2,Δt/2]，频域表示限定在区间 [-Δf/2,Δf/2]，Δt和Δf分别为信号的时宽和带宽.为了解决量纲不同的问题，引入尺度因子S，将新的尺度化坐标定义为

经量纲归一化后的新坐标系（x,v）量纲为1，信号被限定在 [-Δx/2,Δx/2]和 [-Δv/2,Δv/2]中：

令时宽Δt＝T，频宽Δf＝fs，其中T为观测时间，fs为采样频率，则有

① 首先信号x(t)被chirp信号调制，以为采样间隔并利用Shannon内插公式可得

② 将式（11）代入定义式（5）化简可得

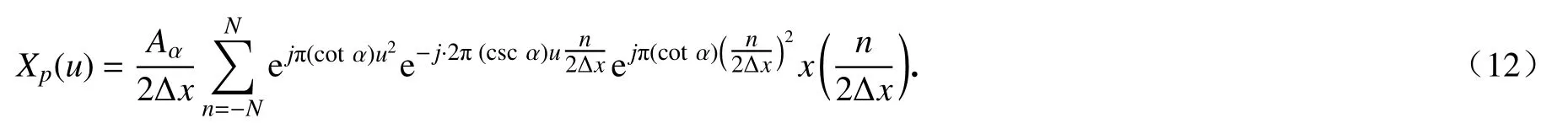
③ 从式（12）可以看出时域变量已经离散化，而分数阶Fourier域变量仍是连续的，类似于离散时间Fourier变换的定义，可以认为式（12）为离散时间FRFT.下面令u ＝m/(2Δx)，将分数阶Fourier域变量离散化，代入式（12）得

进一步将式（13）化简得

式中－N≤m≤N.求和部分为离散卷积形式，从而可以借助快速Fourier变换进行快速计算.

2 分数阶Fourier变换瞬时频率识别

由分数阶Fourier变换特性可知，分数阶Fourier变换是一个时频算子，分数阶Fourier变换域是一个时频域，而旋转角度α是连接信号在时（频）域与分数阶Fourier域的桥梁，因此讨论参数α在信号瞬时频率求解过程中的作用很有必要.式（5）中，当信号的幅值最大时，其对应的最佳分数域坐标u与 旋转角度α有一定的关系，求解过程分为如下步骤.

由式（5）可知核函数 Kα(t,u)与分数域变量u和 旋转角度α有关，则 Kα(t,u)对α求偏导数为

因此可以得到

已知

将式（17）代入式（16），可得

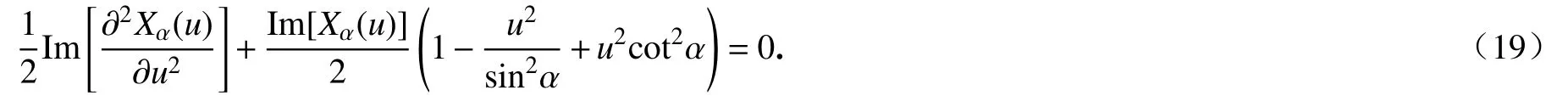
进一步化简得

式（20）为信号分数阶Fourier变换系数最大时，对应的分数域最佳变量与旋转角度的相互关系.为了信号瞬时频率的求解，令为量纲归一化后每段时间间隔t 的分数域表示，由式（10）可得，对分数阶Fourier变换的定义式表现形式进行改变，当 α≠nπ时，由式（5）得

令

将式（22）代入式（21），可得

其中， gα(t)表示可伸缩变换的窗函数，伸缩系数为 (tan α)-1/2， gα(t-)表示窗函数在时间轴上的平移变换，平移Fourier变换算法本质上是一种普通Fourier变换结合伸缩平移窗的算法.由传统Fourier变换定义可知式（23）中 w′是与信号瞬时频率有关的变量，且一般信号的瞬时频率表达式为

式中，f 表示信号的瞬时频率，u表 示信号分数阶Fourier变换幅值最大时对应的最佳分数域坐标.因此可得信号 x(t)的分数阶Fourier变换的表达式为

其中

经上述分析，得到基于分数阶Fourier变换算法对一般任意信号瞬时频率的识别步骤如下：

① 将一般信号通过式（4）旋转到分数阶Fourier域内；

② 由式（10）可以得到信号的分数阶域和时域表示的相互关系；

③ 通过式（19）得出信号的旋转角度和最佳分数域坐标的相互关系；

④ 由式（26）得到信号最终的时频分布.

因此，结合式（19）、（25）可知分数阶Fourier变换识别信号频率过程中参数间的理论关系为

其识别信号作用原理如图2所示.

图 2 FRFT识别一般信号的原理示意图Fig. 2 Schematic diagram of general signal identification based on the FRFT

任意非平稳信号经分数阶Fourier变换后，频率f 关于旋转角度及时间t的三维曲面表示如图3所示，其时频变化曲线，即图3的投影平面如图4所示.

图 3 任意非平稳信号关于频率的三维曲面图Fig. 3 The 3D surface of any non-stationary signal with respect to the frequency

图 4 任意非平稳信号时频曲线Fig. 4 The time-frequency distribution of arbitrary nonstationary signals

3 数值验证分析

3.1 非线性调频模拟信号

假设一非线性调频模拟信号，信号表达式为

参数取值分别为：振幅 A = 1.5 m，初始频率 f0= 15 Hz ，参数 K1= 3.5， K2= 1，观测时间为 [0,10] s，采样频率为fs= 800 Hz. 图5为分别加了噪声（信噪比（ SNR））-10 dB，10 dB，20 dB的非线性调频模拟信号的时域波形.

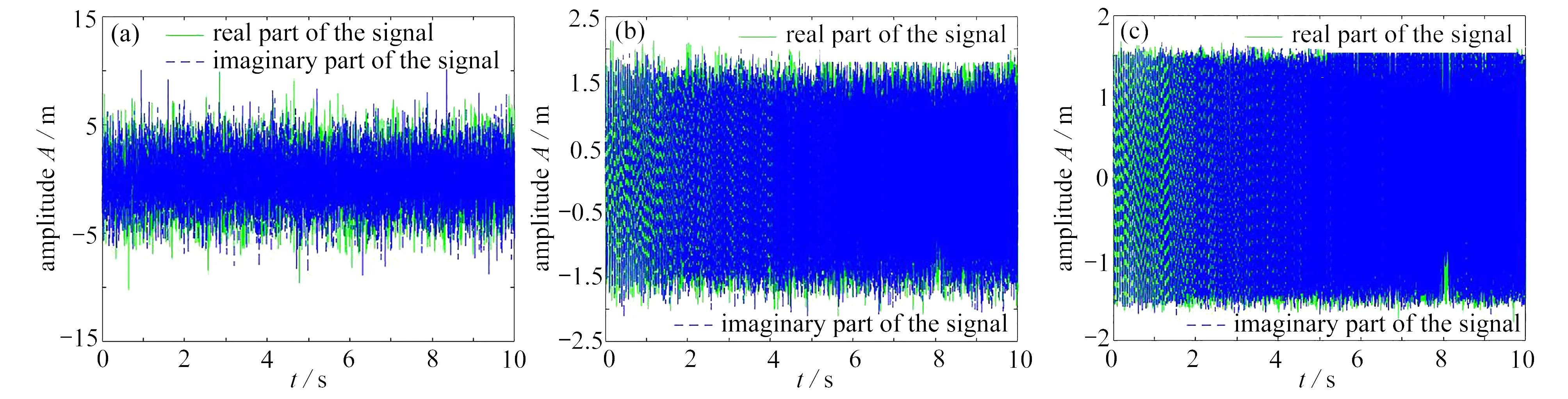
图 5 加噪信号时域波形：（a）SNR为-10 dB；（b）SNR为10 dB；（c）SNR为20 dBFig. 5 Time domain waveforms of noised signals: (a) SNR is -10 dB; (b) SNR is 10 dB; (c) SNR is 20 dB

图 6 FRFT对信号瞬时频率的识别过程：（a）α与最佳关系曲线；（b）时间与α关系曲线；（c）时间与最佳关系曲线Fig. 6 The FRFT identification process of signal instantaneous frequencies: (a) the relationship curve between α and; (b) the relationship curve between t and α;(c) the relationship curve between t and

图 7 FRFT与STFT对信号瞬时频率的识别与理论值的对比：（a）SNR为-10 dB； （b）SNR为10 dB； （c）SNR为20 dBFig. 7 The comparison between FRFT and STFT identification values of signal instantaneous frequencies and theoretical values: (a) SNR is -10 dB;(b) SNR is 10 dB; (c) SNR is 20 dB

图6为分数阶Fourier变换识别瞬时频率过程，分别展示了在不同信噪比条件下，与信号的瞬时频率有关的各个参数间的相互关系.其中，为了凸显本文提出的分数阶Fourier变换算法的优越性，得到基于短时Fourier变换与分数阶Fourier变换的信号瞬时频率识别结果与理论值对比图，如图7所示.从图中可知，在不同的信噪比条件下，FRFT（虚线）对比于STFT（实线）而言，更接近于信号的理论值（点线），表明了分数阶Fourier变换能更好地识别出模拟的非线性调频信号的频率变化规律，结果分析可知，本文方法识别出的瞬时频率与理论值吻合良好，且方法具有一定的抗噪能力，相对比于短时Fourier变换而言在识别精度上有一定的优越性.

3.2 时变结构数值算例

如图8所示的三自由度质量-弹簧-阻尼线性时变系统， m1= m2= m3= 1 kg， k1= k3= 500 N/m，c1= c2= c3=c4= 0.15 N·s·m-1，假定刚度 k2，k4随时间线性变化，具体变化如下式所示：

根据“冻结法”假定结构参数在小的时间间隔内保持不变，为时不变系统，可计算出不同时刻系统的三阶固有频率，如图9所示，作为系统频率的理论值.

图 8 三自由度线性系统Fig. 8 The 3DOF linear system

图 9 刚度线性变化时结构固有频率Fig. 9 Natural frequencies of the structure with linearly changing stiffness

为模拟出图8所示系统的响应信号，假定系统初始条件 x1(0) = 0.3 m， x2(0) = -0.06 m， x3(0) = 0.01 m，为提高计算效率，采用自适应变步长的四阶Runge-Kutta法求解结构的位移响应，即使用较大的步长求解变化较慢的位移响应以提高计算速度，反之使用较小的步长求解变化较快的位移响应以提高计算精度.由于计算过程中时间步长的不同，可先采用样条插值法拟合得到位移响应，再以200 Hz的采样频率得到等步长的结构位移自由响应，采样时间为20 s.

为模拟实际噪声的影响，对离散的响应信号添加信噪比为20 dB的Gauss白噪声，加噪后质量1的位移响应如图10所示.对加噪后的位移响应信号进行分数阶Fourier变换，识别出结构的三阶频率与其对应的理论值对比图分别如图11~13所示.

结果表明，本文建立的基于分数阶Fourier变换的瞬时频率识别方法，用时变结构位移响应识别出的瞬时频率结果和理论值吻合良好，且该方法具有一定的抗噪性能.

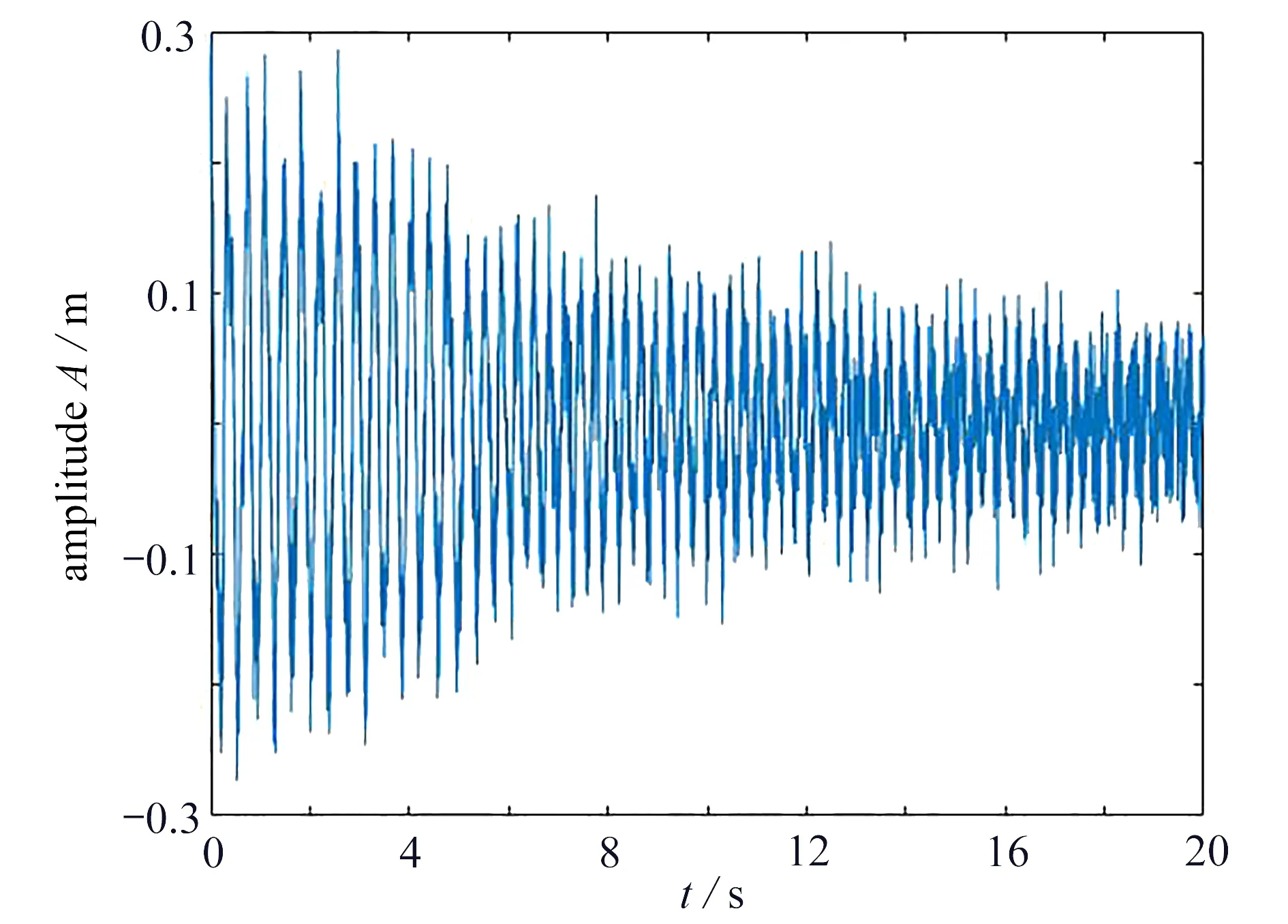
图 10 质量1的位移响应Fig. 10 The displacement response of mass 1

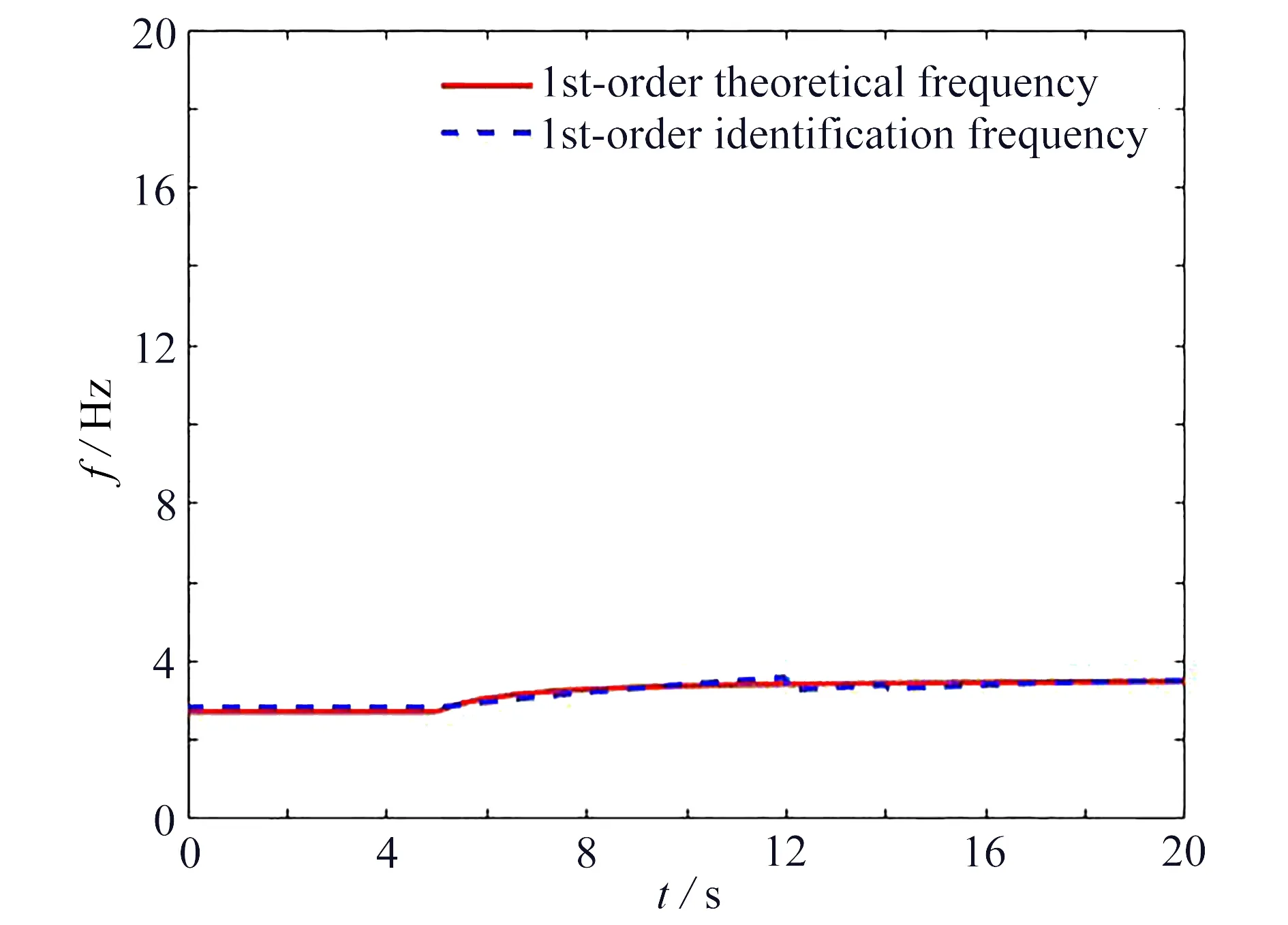
图 11 FRFT识别及理论结构第一阶固有频率Fig. 11 The FRFT-based identification and the 1st-order theoretical natural

图 12 FRFT识别及理论结构第二阶固有频率Fig. 12 The FRFT-based identification and the 2nd-order theoretical natural frequencies of the structure

图 13 FRFT识别及理论结构第三阶固有频率Fig. 13 The FRFT-based identification and the 3rd-order theoretical natural frequencies of the structure

4 结 论

与传统的Fourier变换相比，分数阶Fourier变换增加了一个旋转角度α参数，适用于非平稳信号的处理，具有较好的时频分辨率和局部化特性.本文基于变量α对于分数阶Fourier变换分析信号核心作用进行分析，从理论上解释了分数阶Fourier变换本质上是一种普通Fourier变换结合伸缩平移窗的算法，进而在分数阶Fourier域建立了非平稳信号瞬时频率的一般表达式，实现了结构瞬时频率的识别.采用任意非线性调频信号仿真算例和三自由度有阻尼时变结构系统的数值算例对提出的方法进行了验证，得到如下结论：

1）分数阶Fourier变换在信号处理中的作用相当于普通Fourier变换在分析信号时结合了伸缩平移窗函数，随着窗函数的平移以及弹性伸缩进而得到信号的时频分布.其中起着至关重要的作用是旋转参数p(α= pπ/2)，首先通过旋转参数旋转坐标轴将时域内信号变换到分数阶域内，继而在分数阶Fourier域中，对加窗信号进行常规Fourier计算，窗函数是由旋转参数的正切函数进行伸缩变换的chirp函数.

2）推导出了一般信号瞬时频率的表达式，论证了信号瞬时频率和各个因素的关系.通过模拟和数值算例表明该方法能有一定的抗噪性，识别出的瞬时频率值与理论值能较好吻合，在时变结构的模态参数识别方面具有一定的应用前景.