多气腔软体致动器的弯曲特性分析和试验验证

张珂，魏洪涛，苏凯伦，李青松

(上海应用技术大学机械工程学院，上海 201418)

0 前言

传统刚性机器人虽然已经广泛应用于生活和工业生产中，但随着人类探索的领域越来广、面临的环境也越来越复杂，软体机器人在一些特殊的场合下，相比刚性机器人具有更好的柔顺性和环境适应力。根据驱动类型，可以将软体机器人分为：气动软体机器人、线驱动的仿生章鱼臂、电磁驱动的微型机器人、基于智能材料驱动的软体机器人(例如形状记忆合金和介电弹性体驱动)。目前研究最广泛的一种就是气动软体机器人。气动软体机器人的驱动源易于获取且环保，在没有泄漏的情况下，拥有很高的传动效率。现在已经广泛应用于机械手爪、康复手套、按摩机器人、海产品抓取等领域。

气动软体机器人最重要的组成部分就是软体致动器。现在气动软体致动器按照动作类型可以分为：伸长收缩、弯曲、扭转、螺旋或缠绕型等。按照结构类型可以分为：气动网格致动器、多气腔软体致动器、变刚度软体致动器等。

FARROW和CORRELL基于单向气动增强纤维软体致动器，在其中集成了应变和压力传感器，将这些传感器整合到同一个致动器中，可以实现致动器曲率和环境接触力的本体感知。CONNOLLY等设计一种复合式的增强纤维仿生手指软体致动器，可以实现单向弯曲、径向延伸、横向膨胀等动作，并且提出了一种设计策略，该策略以运动轨迹为输入，并使用基于非线性弹性和优化的分析建模来确定致动器的最佳设计参数。POLYGERINOS等基于增强纤维制备了单向软体致动器和一套系统的设计规则，通过了解软体致动器的输出是如何随着几何参数和输入压力而变化的，从而帮助创建软体致动器，并且对软体致动器进行了弯曲性能和伸长性能测试。

田德宝等在气动网格致动器的基础上，设计了一个变气腔体积的气动网格致动器，提高了软体致动器的形变能力和刚度，使得软体手爪具有更强的夹持力。董虎等人以人舌头为研究对象，设计了气动软体仿生舌，可实现吐舌、翻舌、卷舌等仿生动作。谢荣臻等设计了一个三维弯曲致动器，根据力矩守恒，建立弯曲理论模型。邵城、滕燕基于对蚯蚓的研究，设计了一个环纵肌复合的气动仿蠕虫机器人，纵肌结构中嵌入了金属环限制致动器的径向膨胀，实现对蚯蚓运动的模拟。顾苏程等设计了一个纤维增强型软体夹持器，增强纤维以0°的方式缠绕，其中夹持器还附带了一个真空吸盘，增大了夹持器的负载能力。陈刚等人提出了可弯曲柔性肠镜末端软体致动器，通过控制其弯曲方向与角度，从而用于肠胃检查等医疗领域。

虽然现在软体致动器有了较为广泛的研究，但是增强纤维式多气腔软体致动器的研究还较少。本文作者提出的四气腔增强纤维软体致动器相比三气腔增强纤维软体致动器，在保持原有的全向弯曲功能的同时，当需要沿向前、向后、向左、向右弯曲时，四气腔软体致动器的弯曲控制更加容易，更加适用于面向复杂环境的运动软体机器人等领域。增强纤维相比金属环，能够更好地抑制气球效应。基于Yeoh模型能量密度分布函数，通过几何关系和虚功原理，推导出软体致动器的力学弯曲模型，得到了影响软体致动器的主要因素;采用有限元分析的方法，初步验证了软体致动器的弯曲性能;搭建了一套能够调节流量大小的气动-电路控制系统，能够适用于各类小流量气压驱动的软体致动器的验证和控制；通过样机试验，测试了软体致动器的弯曲性能，验证了理论模型和仿真的准确性和可靠性；采用BP神经网络对软体致动器的角度进行预测，提高了控制精度，为后续以软体致动器为基本单元的软体机器人设计提供了理论支持。

1 软体致动器结构设计和制备

气动软体弯曲致动器本体多采用硅胶制成。其工作原理是:通过对致动器内部气腔施加气压，使得气腔内部受力后，局部产生较大的形变。由于应变限制层或者其他未被加压的气腔在加压过程中形变较小，导致两者产生的形变量不均匀，使得致动器向形变量小的一侧产生弯曲。

1.1 软体致动器设计

软体致动器内部结构如图1(a)所示，气腔分布如图1(b)所示，4个气腔沿着圆周均匀分布。如果对其中一个气腔进行加压，可以使得软体致动器朝着一个方向弯曲。如果对多个气腔(小于4个)施加不同的气压，则可以实现全向弯曲。

图1 软体致动器结构

由于软体致动器的制备材料为硅胶，材质较为柔软，在气腔内施加气压后，如果对致动器的径向不加以限制，会导致气球效应的产生。采用在外侧缠绕凯夫拉纤维的方式，不仅能消除气球效应，也能增加驱动效果以及软体致动器的结构强度和负载力。采用双螺旋对称的方式缠绕可以避免软体致动器产生扭转。软体致动器的设计参数如表1所示。

表1 软体致动器的参数

1.2 软体致动器制备

软体致动器制备采用浇注的方式，制备步骤如图2所示。

图2 致动器制备步骤

为保证软体致动器的气密性，采用了一次性浇注。模具主要包含了底座、外侧模具、气腔模具、上盖，如图3所示。

图3 致动器制备模具 图4 软体致动器样机

根据文献[15]，采用同一厂家的液体硅胶E620，邵氏硬度为A20。将液体硅胶的A、B两组成分按照1∶1混合后，放入真空脱泡机。液体硅胶经过脱泡处理，使其内部更加致密。

当硅胶凝固以后，硅胶和模具之间会产生较大的摩擦力，如果强行脱模会导致模具损坏。因此在液体硅胶注入模具前，需要在模具表面涂抹工业凡士林，便于固化以后的脱模。

模具组装完成后，向模具中倒入混合以后的液体硅胶，再将其放入45 ℃干燥箱中，加快硅胶固化。最后将固化好的软体致动器的表面用纤维线进行缠绕。实物样机如图4所示。

2 软体致动器的力学和有限元分析

2.1 材料本构关系和能量密度函数

橡胶材料作为一种高分子非线性超弹性材料，其本构模型分为两类：一类是基于连续介质唯象理论模型，有Mooney-Rivlin模型、Neo-Hooke模型、Yeoh模型等；另一类是基于热力学统计方法的超弹性本构模型，有高斯统计模型和非高斯统计模型两种。Yeoh模型能用简单的单轴拉伸试验数据描述其他变形的力学特性，具有较良好的拟合橡胶大变形的能力。

基于Yeoh模型的硅橡胶材料的应变能函数为

=(,,)

(1)

(2)

式中：、、为变形张量不变量；、、分别为轴向、周向和径向主拉伸比。Yeoh模型的典型二项参数形式为

=(-3)+(-3)

(3)

式中：、为材料的拉伸系数。

2.2 软体致动器弯曲建模

在受力过程中，假设：(1)硅胶材料具有各向同性和不可压缩性；(2)在弯曲过程中软体致动器的几何外形保持圆柱状；(3)弯曲过程中均保持常曲率弯曲；(4)纤维线不可伸长，而且与驱动器外表面始终保持接触。

软体致动器内含有多个驱动气腔，这里对单气腔弯曲进行建模分析，变形后的形状如图5所示。假设工作气腔所对的气腔轴线等于致动器原长，致动器中心轴线长度为变形后致动器长度。

图5 软体致动器形变

当4个气腔中的1个气腔加压受力时，用驱动气腔的4个象限点到致动器外圆距离(、、、)平均距离表示周向的变化率。

因此致动器在3个方向上的应变可以表示为

(4)

(5)

式中：为工作气腔轴线长度；为中性层长度；为原始致动器原始长度；为变形后致动器外圆半径；为变形前致动器外圆半径；、、、为变形前的4个象限点到致动器外圆距离。

假设纤维线始终缠绕在致动器表面且具有不可拉伸性，纤维缠绕线的长度为，缠绕圈数，拉伸弯曲后的半径为。纤维变形如图6所示。

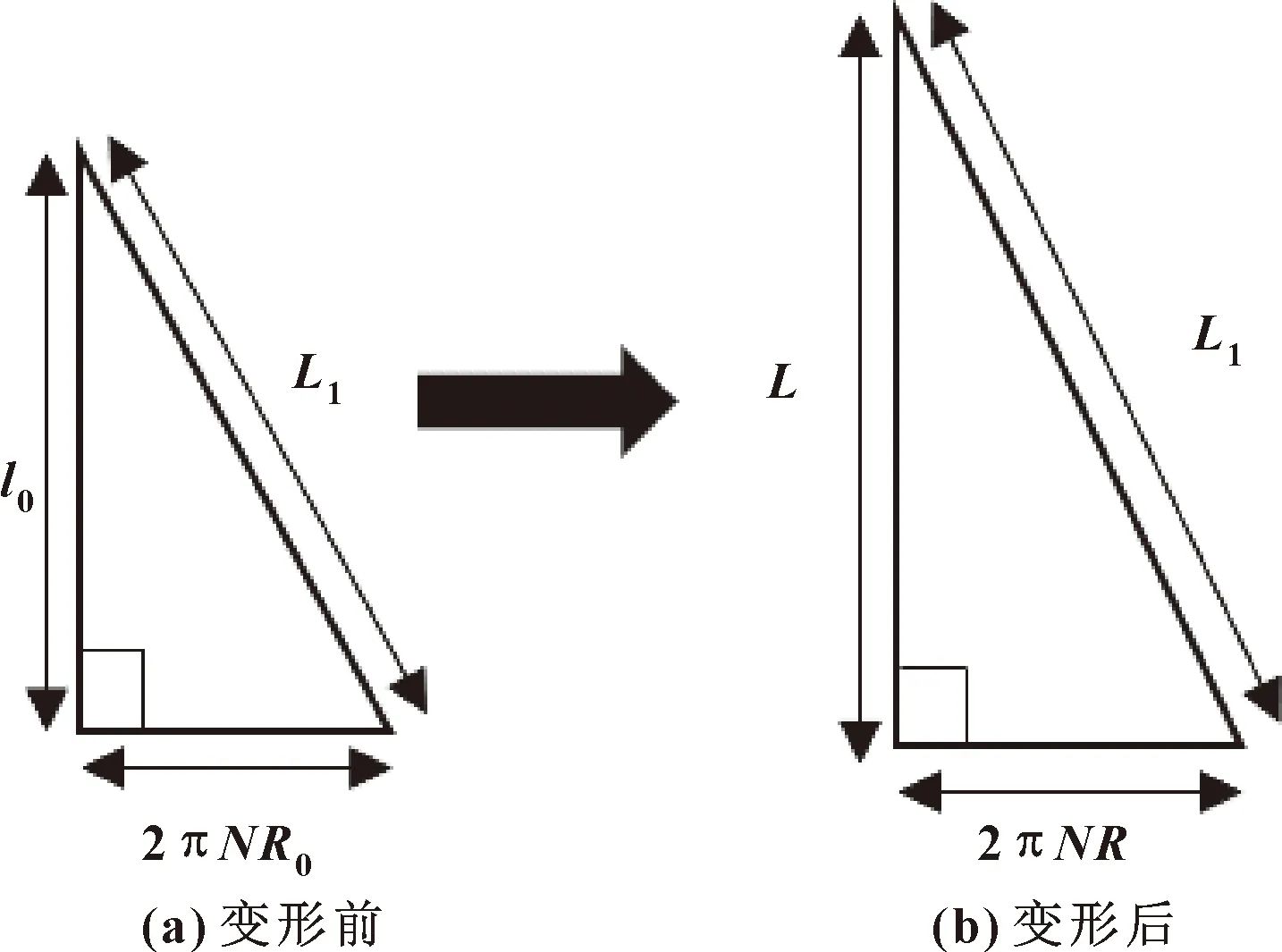
图6 变形前后纤维长度L1与半径R的关系

由几何关系可得：

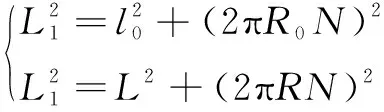
(6)

变形前，硅胶的体积可以表示为

(7)

当软体致动器充气弯曲时，硅橡胶体积与内部气压所占体积分别为

=π

(8)

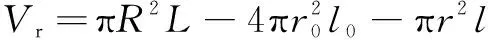
(9)

由于硅胶的不可压缩性，变形前所占的体积与变形后所占的体积保持不变，可知:

=

(10)

联立上式可得：

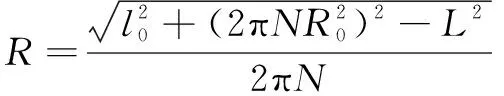
(11)

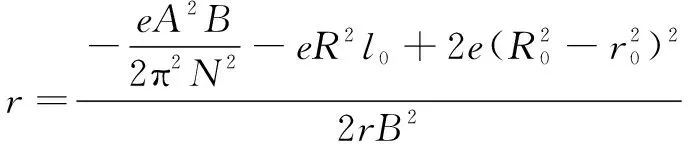
(12)

式中：=(+);=+2。

根据虚功原理，在无外力作用，软体致动器的弯曲变形来源于驱动压力和大气压合力所做的功。考虑软体基体中应力分布的不均匀性，且驱动气压和大气压对软体致动器的影响不一，引入影响系数、，由此可得：

(+)d=d

(13)

联立求解可得：

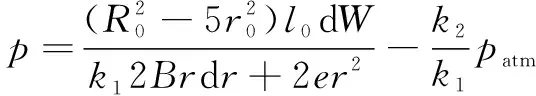
(14)

其中：=+2。

由式(14)可得气压与弯曲角度的关系。可以看出，软体致动器的弯曲性能和基本参数、、、有关。

2.3 有限元仿真分析

通过有限元分析的方法，可以验证软体致动器原理的正确性和软体致动器的弯曲性能。采用Abaqus软件，分别对软体致动器本体和纤维线完成建模。软体致动器的材料设置为超弹性材料。材料拟合方式选择Yeoh。根据文献[15],材料参数=0.052、=0.009。纤维线的材料属性设置为弹性体，其中弹性模量=31 067 MPa，泊松比=0.36。因为软体致动器的变形为大变形且呈现非线性，需定义几何非线性。网格划分时，将模型中软体致动器的单元属性设置为十节点二次四面体单元(C3D10H)；纤维线的单元属性为三节点二次空间梁单元(B32)。在加载过程中，使用绑定约束(TIE)将纤维线始终附着在软体致动器表面上。施加载荷时，将软体致动器一端完全固定，作用力施加在气腔中。

软体致动器的弯曲效果如图7所示。仿真结果表明：对软体致动器的一个气腔进行加压时，软体致动器会朝着对面一侧弯曲。在130 kPa的气压下，软体致动器的弯曲角度为72.9°。

图7 有限元仿真结果

根据节点的坐标值，可以得出驱动气腔在不同压力下的末端轨迹如图8所示，软体致动器在小范围的空间内，具有较强的灵活性。仿真末端轨迹和模型轨迹趋于一致。

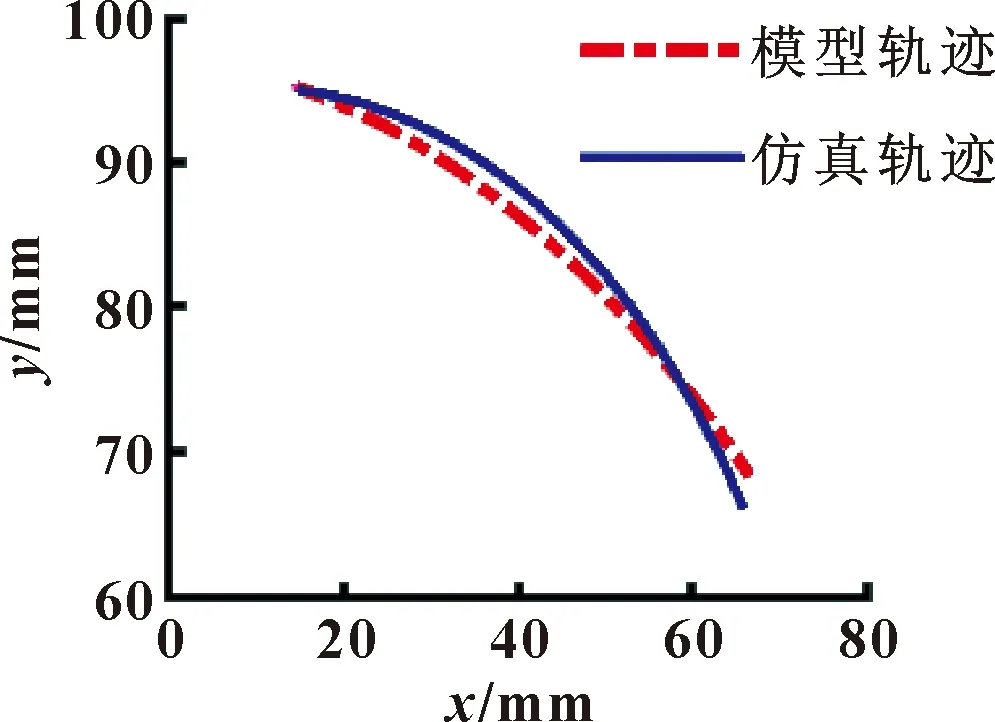
图8 软体致动器末端轨迹

在Abaqus软件的场变量输出中，选取加载气腔的圆心为节点，可得到变形前后坐标。设为圆心，坐标为(0，0)，变形前节点的坐标(，)，变形后′的坐标(，)，如图9所示。

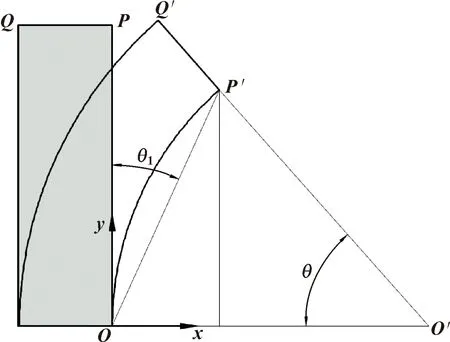
图9 软体致动器弯曲角度

根据几何关系可得有限元分析中，软体致动器的弯曲角度(直线′′与轴的夹角)为

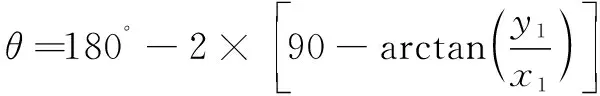
(15)

3 试验验证

3.1 气动试验台搭建

试验台如图10所示，由气动回路、电路控制、上位机组成。气动回路主要包含了两位三通电磁阀、两位两通电磁阀、气动三联件、节流阀和单向导通阀等，气源由空气压缩机或者气泵提供。采用MATLAB GUI进行上位机的编写。上位机通过Arduino控制MOS场效应管，以此驱动电磁阀组，改变气腔内的气压，使软体致动器产生形变。在软体致动器的活动端面安装了一个倾斜传感器，测量弯曲角度。将Arduino作为数据采集器，采集气压和倾角传感器的数值。出气口同时连接了软体致动器和气压传感器。控制系统如图11所示。

图10 试验平台

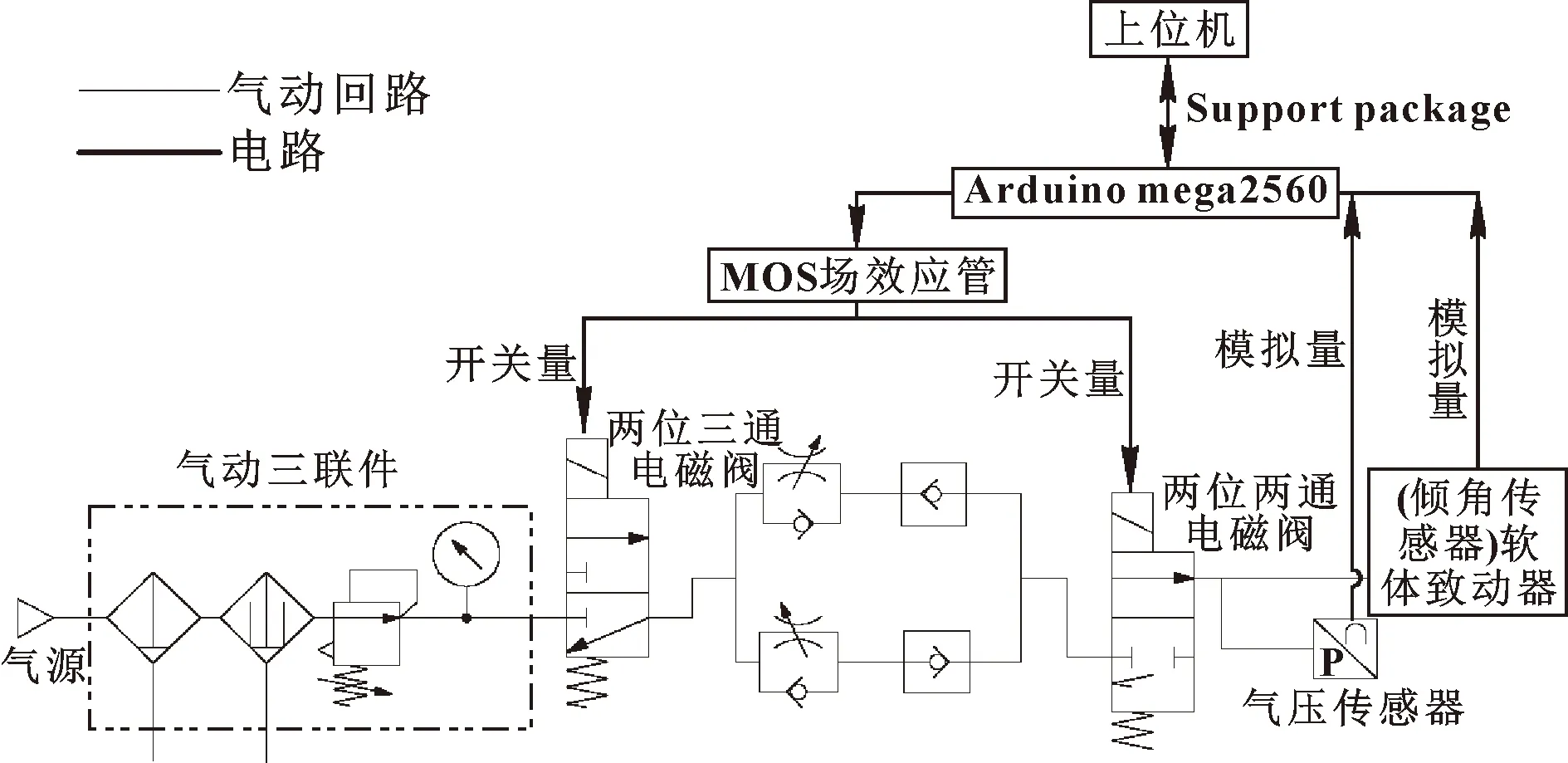
图11 控制系统

3.2 软体致动器弯曲测试过程

基于上述的试验平台，上位机通过调用控制函数，可以实现自动精准测量。试验中，由于4个气腔为均匀分布，因此选取其中一个气腔作为加载气腔，验证单气腔驱动下的弯曲性能。从0 kPa开始，缓慢连续加压，每增0.5 kPa，记录一次气压和角度的数值，到110 kPa为止。

3.3 基于BP神经网络的弯曲特性预测

由于软体致动器的气压和角度成非线性关系，且本身的弯曲性能容易受到材料、制备工艺的影响，所以对软体致动器的控制造成了很大的困扰。BP网络可以实现从输入到输出的任意非线性映射。根据实际数据训练出来的BP神经网络，可以拟合出软体致动器的气压和角度的非线性关系。

根据第3.2节中的方法，将得到的数据作为BP神经网络的训练样本。为了更好地拟合软体致动器的弯曲特性，采用双层BP神经网络，其神经网络的结构如图12所示。把气压作为输入，角度作为输出，建立单输入单输出的神经网络模型。

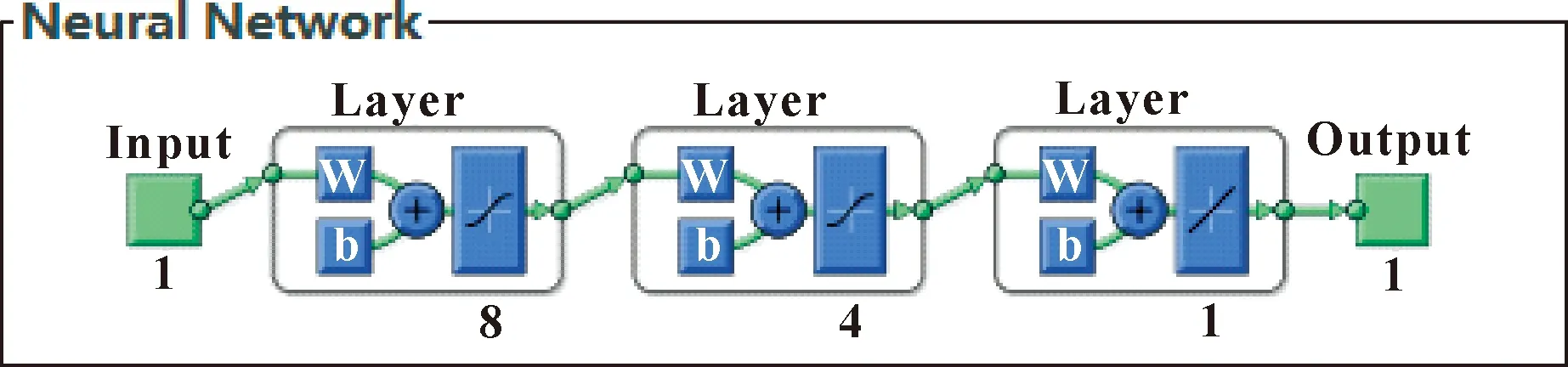
图12 BP神经网络结构

其中，隐含层的传递函数设为tansig，输出层传递函数设为purelin，训练函数设为trainlm。迭代次数设为1 000。

将训练好的神经网络放入上位机程序中，自动对软体致动器进行加载试验。从10 kPa开始，每间隔7 kPa进行一次数据采集。将采集到的实际气压代入训练好的BP神经网络中，进行角度预测，再用测量数值和预测数值做差，验证预测效果。

3.4 试验结果分析

为了确定力学模型中的影响系数，采用分析试验数据的方法来确定影响系数。将试验数据进行分析和拟合，得出影响系数=2.55、=6.50。将修正系数代入式(14)中，可以得到软体致动器的力学弯曲模型；将有限元分析中得到的坐标数据代入式(15)中，由此可以得到模型曲线、试验数值、仿真曲线。其结果如图13所示。

从图13可以发现：在110 kPa的气压下，软体致动器的弯曲角度为62°，说明软体致动器具有良好的弯曲特性，且能够满足大部分使用情况；模型数值与试验数据相比，在95 kPa的时候，最大的误差为3.42°，误差占比为8.57%。试验证明了在0～110 kPa内，理论计算值能较好地反映出软体致动器的弯曲特性。

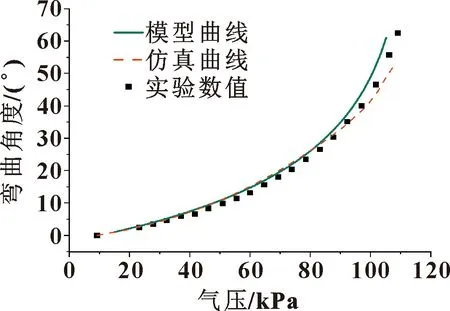
图13 模型曲线、试验数值、仿真曲线

数学模型、有限元分析相对试验数据的误差来源于材料本身属性不够稳定，因为经过加载和卸压后，软体致动器基体还有一定的残余应力，在相同气压下，每次弯曲角度会略有不同；当软体致动器的弯曲角度过大时，软体致动器的形状不再近似看作圆形；因为加工工艺的原因，两根对称螺旋缠绕的纤维线没有完全对称，使得软体致动器产生一定的扭转,导致有限元分析、力学模型和试验数值产生了误差。

从图14可以看出：在不同气压下，预测角度和测量角度的误差百分比最大为2%，角度误差在1°以内，说明BP神经网络相比数学模型能够更好地拟合出软体致动器的气压和弯曲角度之间的非线性关系，能够有效提高控制精度。

图14 BP神经网络角度预测

4 结语

根据软体致动器的弯曲原理，设计了一个增强纤维式多气腔软体致动器；基于虚功原理，在无外力的情况下，气压和大气压合力所作的功转换成软体致动器形变所需的能量，据此建立软体致动器的气压和弯曲角的关系；搭建的控制系统，能够满足各类气动软体致动器的驱动和控制需求。基于上述研究和试验分析得出以下结论：

(1)在0～110 kPa内，软体致动器的弯曲角度可以在0°～62°之内连续变化，气压和角度呈现非线性的关系。

(2)力学弯曲模型在一定范围内，能够较好地拟合软体致动器的弯曲特性，误差在8.57%以内。

(3)BP神经网络预测角度和实际角度相差在1°以内，说明该方法能够有效提高软体致动器的拟合精度。同样的，该方法也能够应用于其他类型的软体致动器的性能预测。

(4)通过试验验证了数学模型和有限元仿真的可靠性和准确性，为后续设计提供了理论依据。

设计的软体致动器拥有良好的灵活性用于制造柔性抓手、管道探测、侦察机器人等领域，具有广阔的应用前景。