抗磁悬浮气流能量采集器输出特性分析
王天航,高琳,苏宇锋,程书晗,杨孝峰
(郑州大学机械与动力工程学院,河南郑州 450001)
0 前言
随着近年来越来越多的无线传感器网络应用到偏远地区和人们环保意识的增强,开发出能通过从周围环境获取能量的装置以替代传统电池从而永久地为无线传感器供电成为了一个研究热点。
自然界广泛存在光能、地热能、振动能、潮汐能、气流能等能量。气流作为一种普遍存在的能源受到了许多研究人员的关注。PRIYA等研究了一种基于压电效应的旋转式微型气流能量采集器,采集器使用12个60 mm×20 mm×0.6 mm的双压电晶片,当振动频率为6 Hz时会产生10.2 mW的输出功率。ZHU等开发出一种基于电磁感应的振动式气流能量采集器,启动风速为1.5 m/s,当流速达到2 m/s时,达到90 μW的平均输出功率。YANG等研究出一种基于静电感应的纳米气流能量采集器,该采集器最大输出电压达到100 mV,在外部负载为100 MΩ时输出功率为0.16 mW,可以对风速和风向进行检测,但不适用于高速气流的收集。巩启等人利用抗磁悬浮摩擦小、功耗低等优点,提出一种基于抗磁悬浮的新型气流能量采集器,进行了理论分析和仿真分析,并开展了初步的实验研究。
作者在课题组研究的基础上对抗磁悬浮气流能量采集器的悬浮空间进行研究,分析了能量采集器的平面螺旋线圈的结构参数和布置位置对输出特性的影响。
1 悬浮永磁体悬浮分析
所研究的抗磁悬浮气流能量采集器如图1所示,采集器由外壳、提升永磁体、上热解石墨板、悬浮永磁体转子、平面螺旋线圈、下热解石墨板和气孔组成。
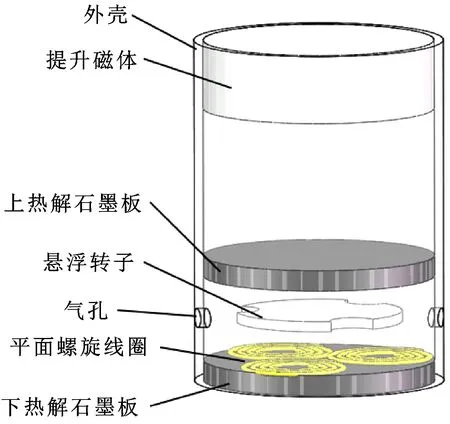
图1 抗磁悬浮气流能量采集器模型
提升磁体(N35)剩磁为1.21 T,尺寸为25 mm×10 mm,上下热解石墨板完全相同,磁化率为(-8,-8,-45)×10,尺寸为25 mm×3 mm。悬浮转子(N52)剩磁为1.45 T,尺寸参数如图2所示,6个绕组相同的线圈分成两组布置在石墨板表面并串联在一起。悬浮转子通过提升磁体的吸引力克服自身重力,并根据肖恩定律,通过引入的上下热解石墨板施予悬浮转子的反馈排斥力,使悬浮转子能够稳定悬浮。当悬浮转子受到外界具有一定流速的气流驱动时,悬浮转子会绕自身轴线稳定旋转,使得平面螺旋线圈内磁通量发生变化,从而产生感应电压。
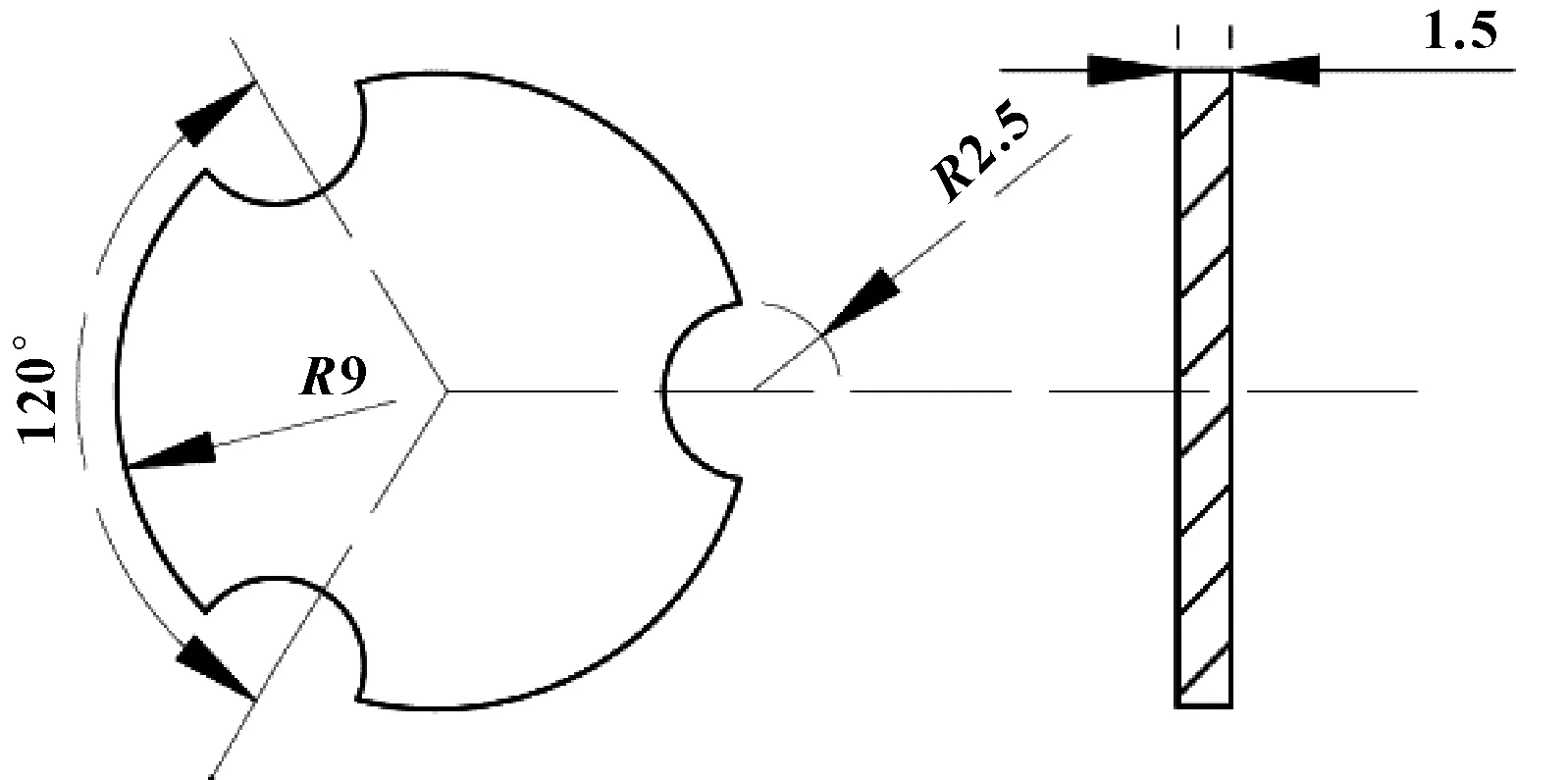
图2 悬浮转子几何参数示意
相较于磁力与重力,抗磁力只有在距离为毫米量级时才表现出明显作用。当热解石墨板板间距超出一定范围,悬浮转子就会由单稳态悬浮过渡到双稳态悬浮,为了保证上下线圈所产生的电压随时间变化完全一致,需要使悬浮转子稳定悬浮在上下石墨板的对称平面。
利用有限元仿真软件COMSOL 5.5计算悬浮转子受到的力,图3是悬浮转子所受的磁力与抗磁力随间距变化曲线。磁力仿真分析如图(a)所示,可以看出:随着提升磁体与转子的间距增大,磁力迅速减小,当悬浮转子与提升磁体间距为74.1 mm时,磁力等于重力。抗磁力的仿真分析如图(b)所示,可以得知:当间距从0 mm增大到2 mm,抗磁力迅速变小,之后抗磁力逐渐趋于平缓,说明抗磁力仅在毫米级别范围表现出作用。
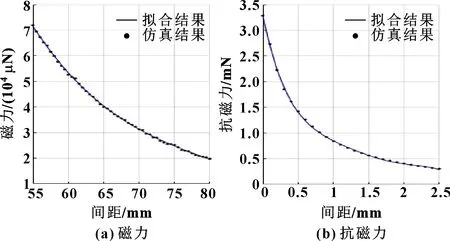
图3 磁力与抗磁力仿真
图4是悬浮转子在不同上下石墨板间距下所受到的合力,其中对称平面为位移零点,并规定向上为正方向。由受力平衡可以知道,悬浮转子在合力等于零的位置保持平衡,随着间距的缓慢增大,悬浮转子的位移-合力曲线也随之变化。当间距为2.3 mm时,曲线近似线性且只有一个零点,当间距为5.5 mm时,曲线呈现出明显的非线性且有3个零点。
对图4中悬浮转子在不同板间距下的合力曲线进行积分处理得到势能曲线,如图5所示。悬浮转子将在势能曲线极小值处保持稳定悬浮,当上下石墨板间距为2.3~3.9 mm时,转子为单稳态悬浮,此时稳定悬浮在上下板对称平面;当上下石墨板间距为3.9~5.5 mm时,悬浮转子为双稳态悬浮,此时悬浮在靠近石墨板位置。
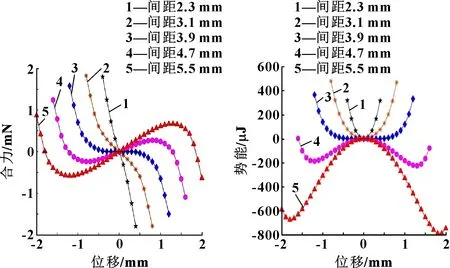
图4 不同板间距下合力与位移的关系 图5 不同板间距下势能与位移的关系
2 线圈布置方案分析
悬浮转子的转速和线圈的结构参数及布置位置是影响线圈所产生感应电动势大小的关键。当线圈一定时,感应电动势和转速呈线性关系,所以只需要研究某个固定转速下感应电动势与线圈几何关系即可。利用COMSOL 5.5对感应电动势进行仿真分析,转子位于板间距2.3 mm的单稳悬浮位置,距上下石墨板皆为0.4 mm,转速设置为2 000 r/min,根据实际尺寸进行建模分析,划分网格后的三维物理模型如图6所示。
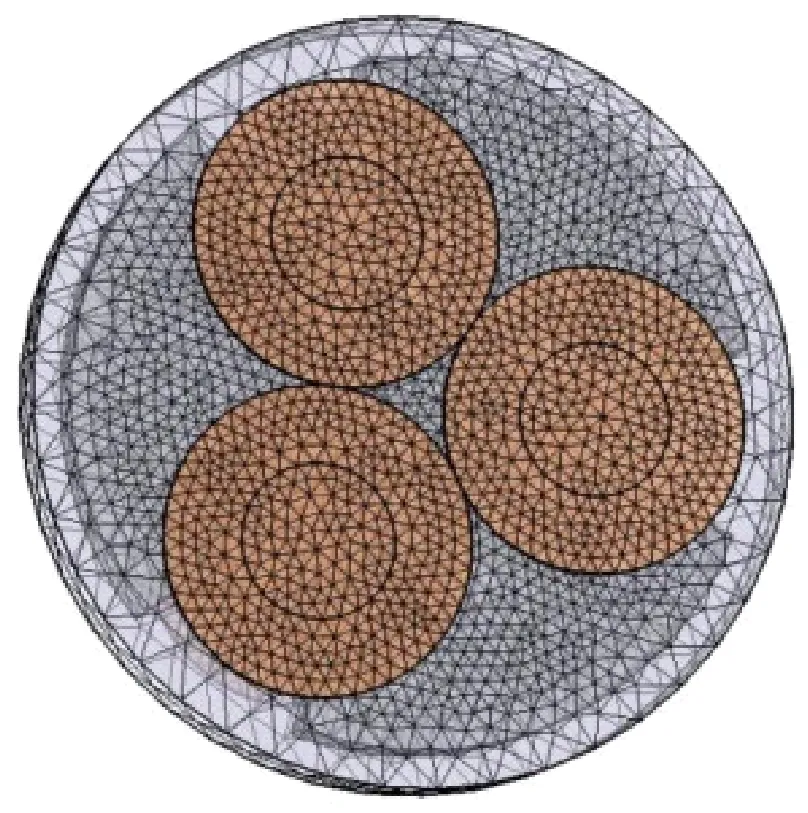
图6 三维物理模型网格划分
如图7所示:图(a)优化后位置为3个线圈初始位置分别布置在转子豁口圆心处,图(b)优化前位置为3个线圈始终相切且中心与转子中心相重合。
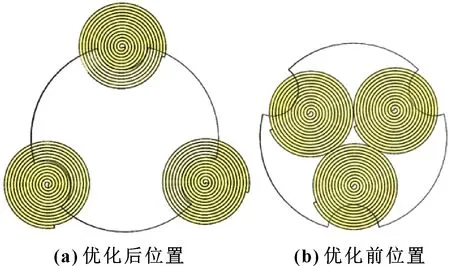
图7 线圈布置位置
在单个线圈内半径为0、外半径不断增大的情况下,优化前位置线圈组所产生的感应电压如图8(a)所示。可以看出:感应电动势随转子的转动,呈现出周期性变化的规律,电动势峰值随着的增大而增大;随着不断增大,感应电动势所表现出来的小峰值特性逐渐减弱,当=6 mm,感应电动势曲线近似正弦曲线,小峰值完全消失。图5(b)解释了小峰值出现的原因,线圈中磁通量在=0.1 s附近单位时间内变化缓慢,根据公式(1),这时候附近的电动势趋近于零,在曲线上呈现出小峰值特性。当越小,磁通量缓慢变化时间越长,小峰值出现的时间越长。
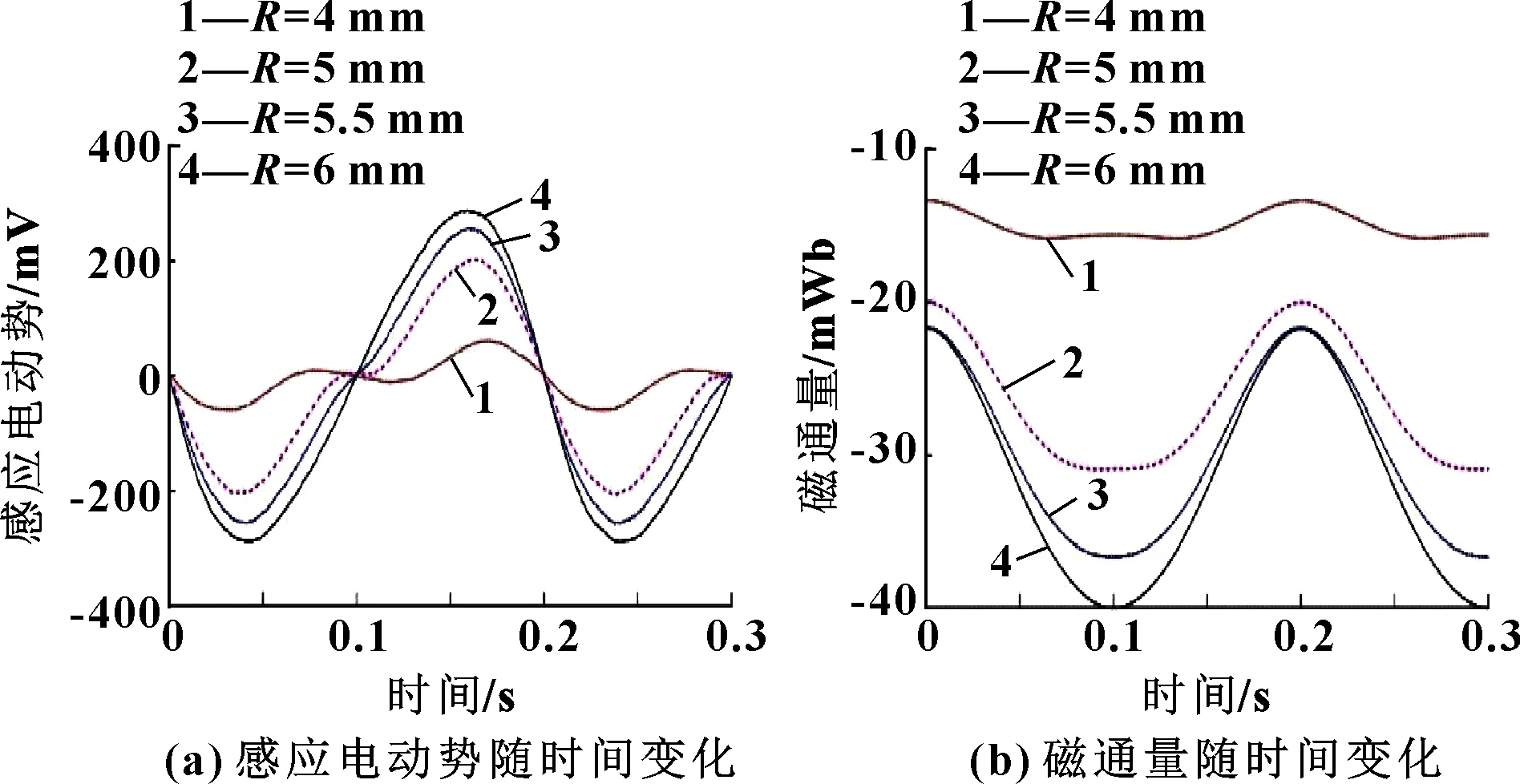
图8 优化前位置部分感应电动势随线圈外径R变化
=-(d)(d)
(1)
优化前后两种线圈布置方案的电动势峰值和电阻随线圈外半径的对比曲线如图9所示,其中=7.78 mm为两种方案重合位置。随着增大,优化后的峰值电压先是近似线性增加,然后趋于稳定值,=6 mm时达到最大电压峰值328.8 mV;当>6 mm时,电压开始缓慢下降。较小时,优化前位置的线圈处于转子中心轴线附近,此时线圈内磁通量变化量极小,因此电压值极小;在中间一定的范围内,峰值电压近似线性增加,趋于稳定后开始减小。当增大到一定程度后,两种位置的峰值电压开始缓慢减小,这是因为随着闭合线圈面积变大,磁通量增加,但磁通量变化速度却减慢,因此峰值电压减小。可以预见,当继续增大,线圈中峰值电压将会持续减小直至不再产生感应电动势。
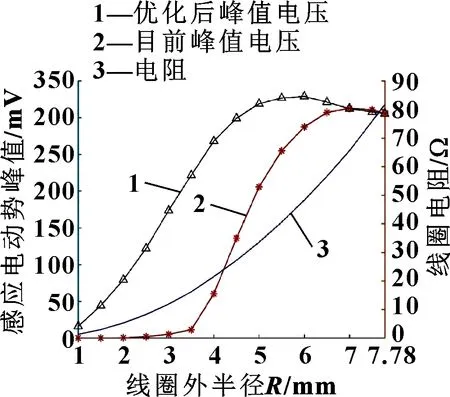
图9 优化前后峰值电压与电阻随R的变化
线圈的平均功率由公式(2)计算:
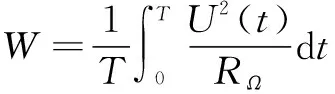
(2)
不同外半径下两种位置所对应的平均功率如图10所示。当线圈外半径较小时,优化后的平均功率迅速增加,在=4.5 mm时达到最大值0.96 mW,随后平均功率开始减小,在电压最大值=6 mm时,平均功率为0.85 mW,与最大平均功率相差11%,此时的峰值电压相差12%。由于优化前方案在较小时电压极小,这个范围内平均功率几乎为零,随着增大,功率同样表现为先增大后减小,且只在6~7.78 mm内,优化前位置的平均功率略大于优化后。
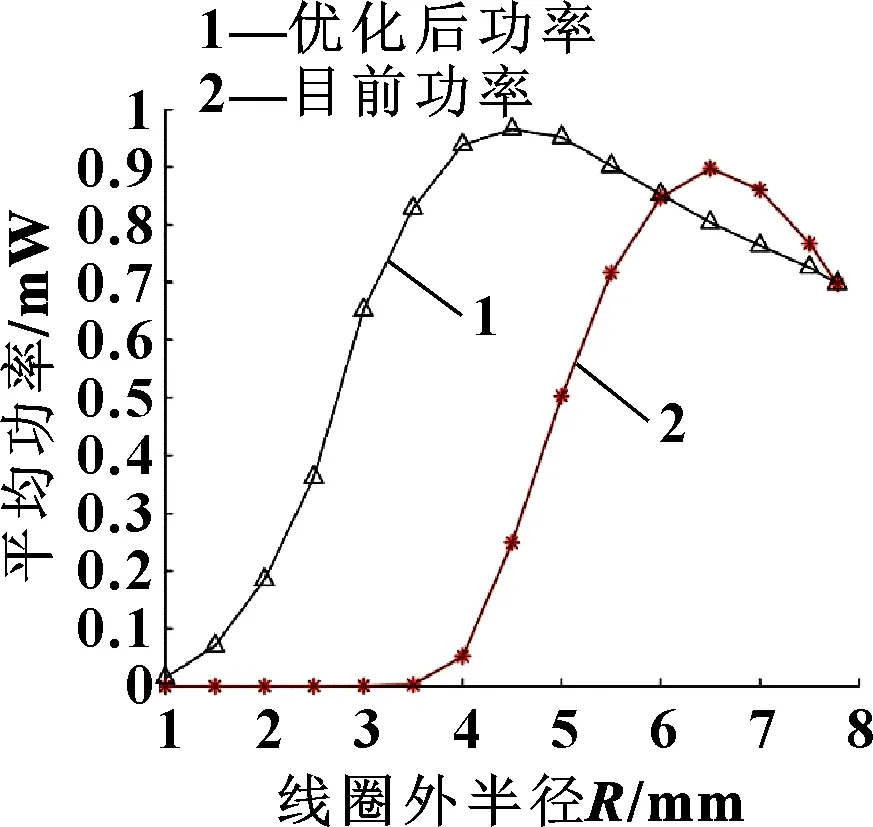
图10 优化前后平均功率随R的变化
由图9、图10可以得出:当线圈半径≤6 mm时,采用优化方案将线圈分别布置在3个豁口的圆心处,将会获得更高的峰值电压和平均功率;当线圈半径>6 mm时,采用优化前方案将线圈相切布置在转子中心轴线处将会得到稍高的平均功率和相等水平的峰值电压。
3 输出特性分析
在同样的线圈外径下,改变制作线圈所用导线的线径将会改变线圈的电阻,并通过改变线圈的匝数进而改变线圈中磁通量变化的速度进而影响感应电压。为了得到更高的峰值电压,令=6 mm,采用a方案布置,图11是感应电压峰值和平均功率随导线线径变化的曲线。
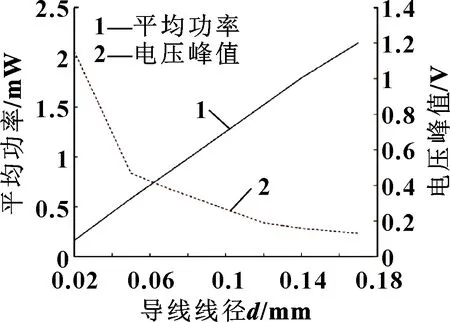
图11 平均功率与电压峰值随线径d的变化
可以看出:保持线圈外径不变时,可以通过减小导线线径的方法获得较大的电压值,但由于线圈所产生的平均功率随着增大,近似线性增长,此时能量采集器获得的平均功率较小。但由于悬浮转子与石墨板间距的限制,导线线径不能过大,当导线线径较小时,可以适当增加平面螺旋线圈的层数来提高平均功率,同时获得最大程度的峰值电压。
能量采集器的结构微型化要求上下石墨板的板间距不能过大。由于此采集器采用了2.3 mm的板间距,考虑到悬浮空间的限制和获得更大的感应电压,选定线圈外径=6 mm,线圈线径=0.02 mm,线圈层数2层,此时线圈匝数为600匝。图12是此种线圈在2 000 r/min下电压与瞬时功率随时间变化的曲线。可以从图中得到此时的电压峰值达到2.33 V,电源平均功率为0.32 mW,瞬时最大电源功率可达0.84 mW。
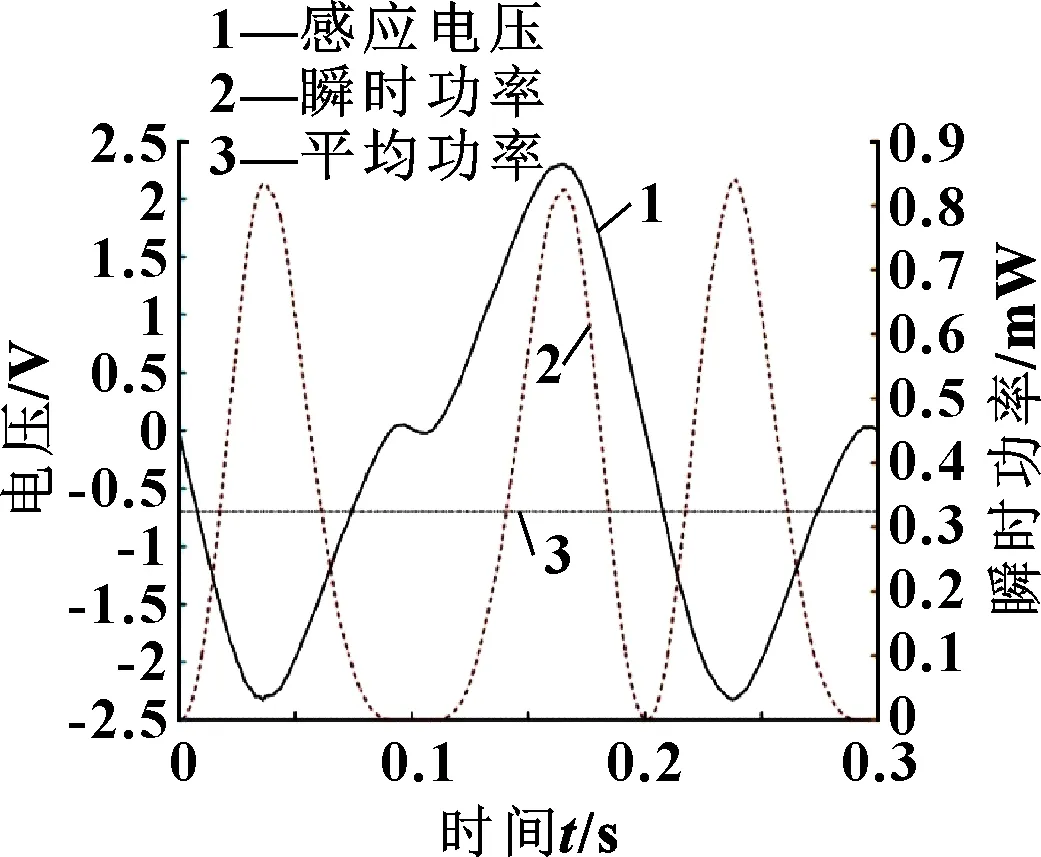
图12 感应电压和瞬时功率随时间变化
4 结论
通过分析抗磁悬浮气流能量采集器悬浮转子的受力情况,得到了适合采集器工作的上下石墨板间距,发现了线圈两种不同布置方案下电压和功率随线圈外径的变化趋势。为了得到更大感应电压同时获得较大的平均功率,选定线圈外径6 mm,导线线径0.02 mm,层数两层时,在2 000 r/min时可得到2.33 V的峰值电压、0.32 mW的平均功率和0.84 mW的瞬时最大电源功率。该能量收集器可用于气流流动能量的收集,对低功耗电子供电。

