基于模糊控制的Y形管内高压成形加载路径优化

续迎萍，崔岸，马浩通，余天明，马耀辉

(吉林大学，汽车仿真与控制国家重点实验室，吉林长春 130000)

0 前言

内高压成形是液压成形技术中的一个重要分支，一般用于管形类零件的塑性成形，由于其特殊的工艺加工方式，加工出的零件具有液压成形的普遍优点，还可以减少零件加工模具，减少焊缝，使加工出的零件整体性强且质量高。

影响管材内高压成形的因素有材料的性能、摩擦及模具的几何结构、轴向进给、内压力等。近年来，内高压成形工艺的研究热点主要为加载路径的优化。目前加载路径优化的方法主要有基于寻优算法的优化法和模糊控制优化法。但寻优算法一般需要进行多次仿真以构建样本库，而模糊控制法仅需要少量的试错仿真，仿真效率高。模糊控制法优化加载路径的关键是成形的评价以及逻辑推理规则的设计，许多学者对此进行了大量研究，如将管材外表面与内表面节点应变的差值作为起皱的评价指标；将管材相邻节点的斜率的变化值、内力功的二阶增量与成形极限曲线(FLC)和FLC与管材底部节点到模具表面的最大距离等作为起皱与破裂的评价指标；采用塑性分叉理论与塑性失稳理论作为起皱与破裂的评价准则；用管材表面与中间冲头在两个正交方向上的接触长度来评价零件的成形程度。

然而，某些评价指标的选取仅适用于仿真后处理获得，在试验设备中无法获取。因此，本文作者选取起皱间隙和贴模长度作为成形评价指标，便于通过传感器获取；按照成形的过程特点，分阶段进行模糊控制系统设计，优化Y形管内高压成形加载路径；通过实例对研究方法进行验证。

1 Y形管内高压成形数值仿真

1.1 Y形管模型建立与内高压成形仿真

根据牛顿冷却定律确定边界条件，利用CATIA软件建立几何模型， 采用HyperMesh软件进行网格划分，然后导入Dynaform软件中进行有限元数值仿真。Y形管有限元数学模型如图1所示。初步选用分段线性加载，加载路径如图2所示，其中有10个参数，取值如表1所示。

图1 Y形管有限元模型

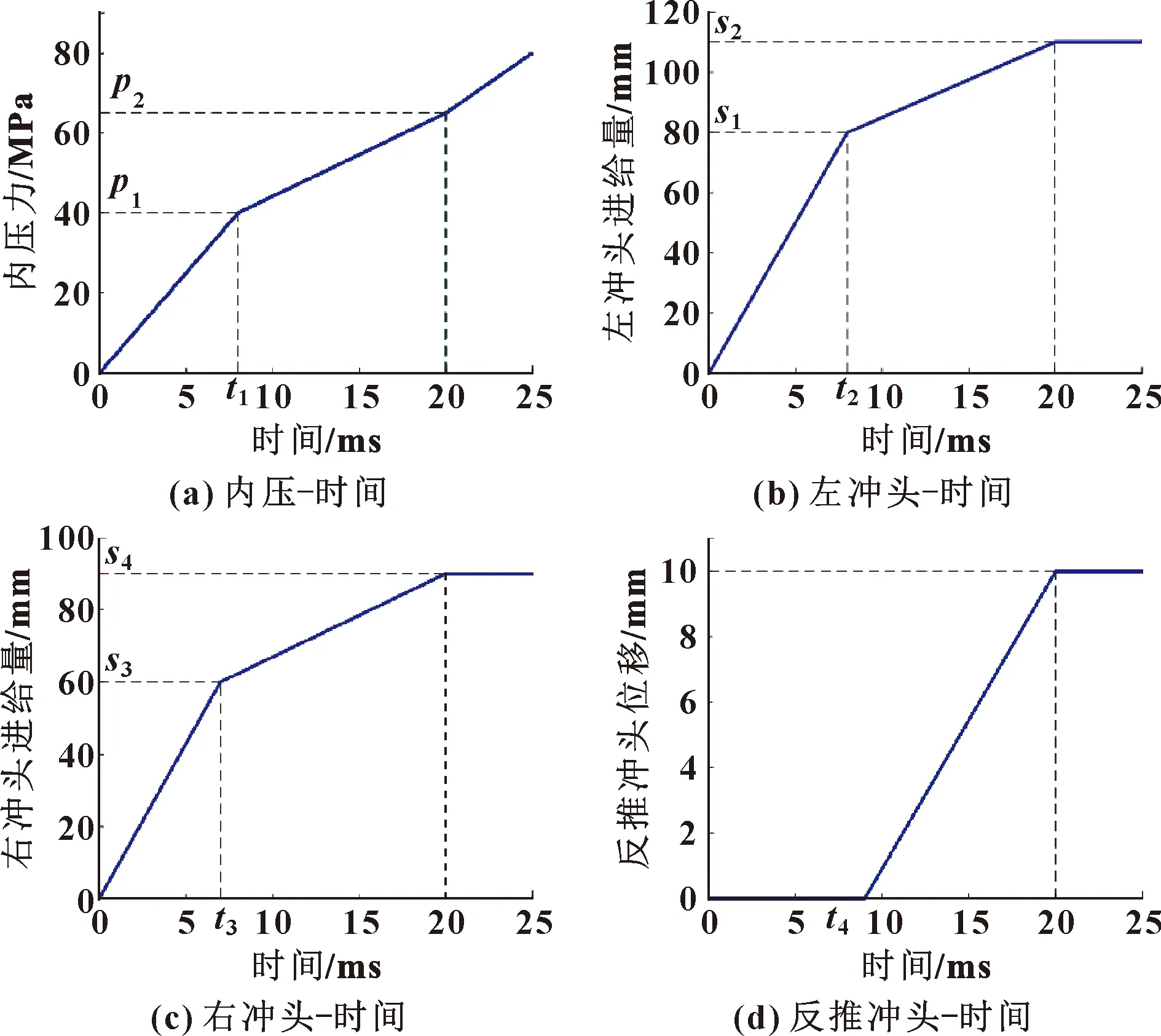
图2 分段线性加载路径

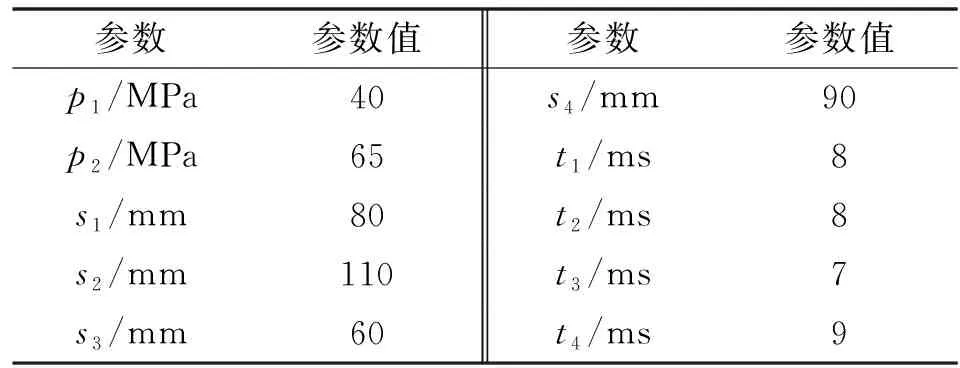
表1 加载路径各参数取值

图3所示为仿真减薄率等值线。可以看到:侧面呈U字形的厚度等值线，厚度等值线以上的材料减薄，厚度等值线以下的材料增厚，最大减薄率为11.6%，最大增厚率为168.435%。值得注意的是圆角处材料增厚较明显，因为圆角部分为过渡区域，材料流动受阻堆积。

图3 仿真减薄率等值线

1.2 工艺参数和几何参数对成形质量的影响

1.2.1 圆角对成形质量的影响

选取3种圆角半径分别为5、15、25 mm，加载路径均为线性加载，图4所示为仿真结果。可以发现：当进给量较大且一定时，圆角半径越大，过渡圆角区域所占空间越大，越不易产生起皱，可以得到较好的成形质量，但圆角半径过大会导致材料利用率低；反之，圆角半径越小，越容易产生起皱缺陷。

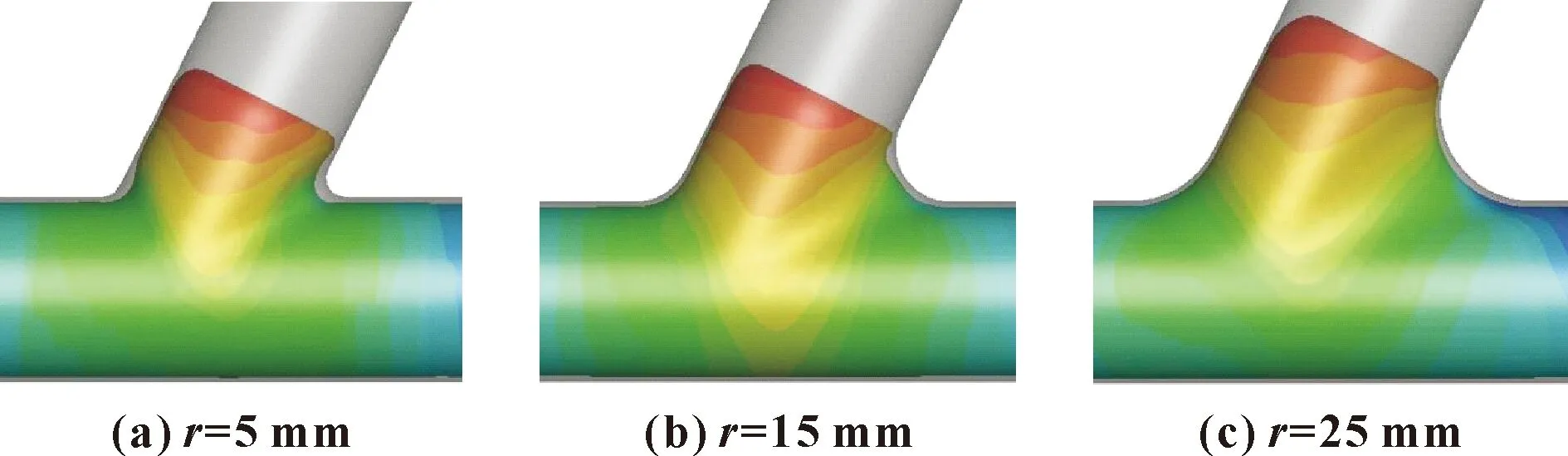
图4 3种圆角半径仿真对比

1.2.2 支管半径尺寸对成形质量的影响

从经验来看，支管尺寸不会对管材的成形有决定性影响。为验证这一点，选取3种支管,半径分别为16、20、24 mm，采用线性加载路径进行分析，结果如图5所示。可知：当支管半径较小时，由于支管空间相对狭窄，当轴向进给量一定时，会导致中部区域材料受挤压更严重，但3种尺寸支管的基本成形特性如起皱缺陷位置、壁厚等值线分布等均基本一致。

图5 3种支管半径仿真对比

1.2.3 摩擦因数对成形质量的影响

选取4个摩擦因数分别为0.01、0.06、0.1、0.15进行仿真分析，结果如表2所示。可知：随着摩擦因数的增大，最大壁厚逐渐增加，最小壁厚逐渐减小，最大厚度差增加，壁厚均匀性变差。

表2 不同摩擦因数对成形质量的影响

1.2.4 加载路径对成形质量的影响

采用试验设计方法，选取加载路径的10个参数作为因子，根据有限元仿真获取此加载模式下各变量的取值范围，将各变量在取值范围内划分3个水平进行正交试验设计，以最大减薄率和支管顶部贴模区域纵剖面长度作为成形质量的评价指标，共设计36组试验。

对正交试验结果进行数据分析，得到各因子极差如表3所示。可以发现:对响应具有显著影响的因子是、、、、、、。

表3 各因子响应极差值

2 基于模糊控制的加载路径优化

2.1 加载路径模糊控制器设计

图6所示为运用模糊控制优化加载路径的循环控制框图。将整个成形过程划分为4个阶段，分别为预成形阶段(第1阶段)、圆角贴模阶段(第2阶段)、充形阶段(第3阶段)和支管成形阶段(第4阶段)。分别对每个阶段进行模糊控制器设计，每个阶段都有不同的成形状态和控制指标。

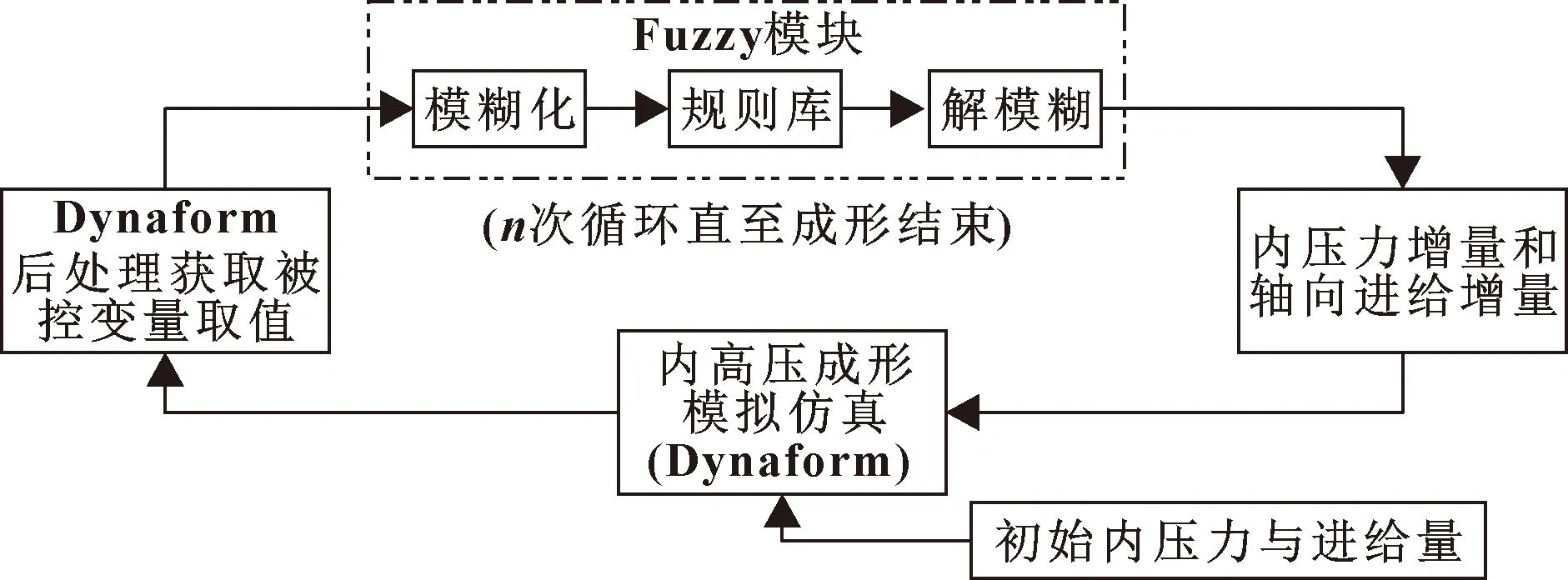
图6 加载路径循环控制框图

2.1.1 第1阶段模糊控制器设计

第1阶段控制系统结构框图如图7所示。输入端为起皱间隙，输出端为内压增量()、轴向进给增量(、)。由于第1阶段无法找到控制变量，因此第1阶段先采用线性加载的方式，给定1个内压和轴向进给的加载速率。试错仿真结果如表4所示，可知:随着内压加载速度逐渐减小，轴向进给速率逐渐增加，底部增厚率明显增加，不易发生起皱现象。若将减薄率作为控制输入，不易用传感器测得。

图7 第1阶段模糊控制系统结构

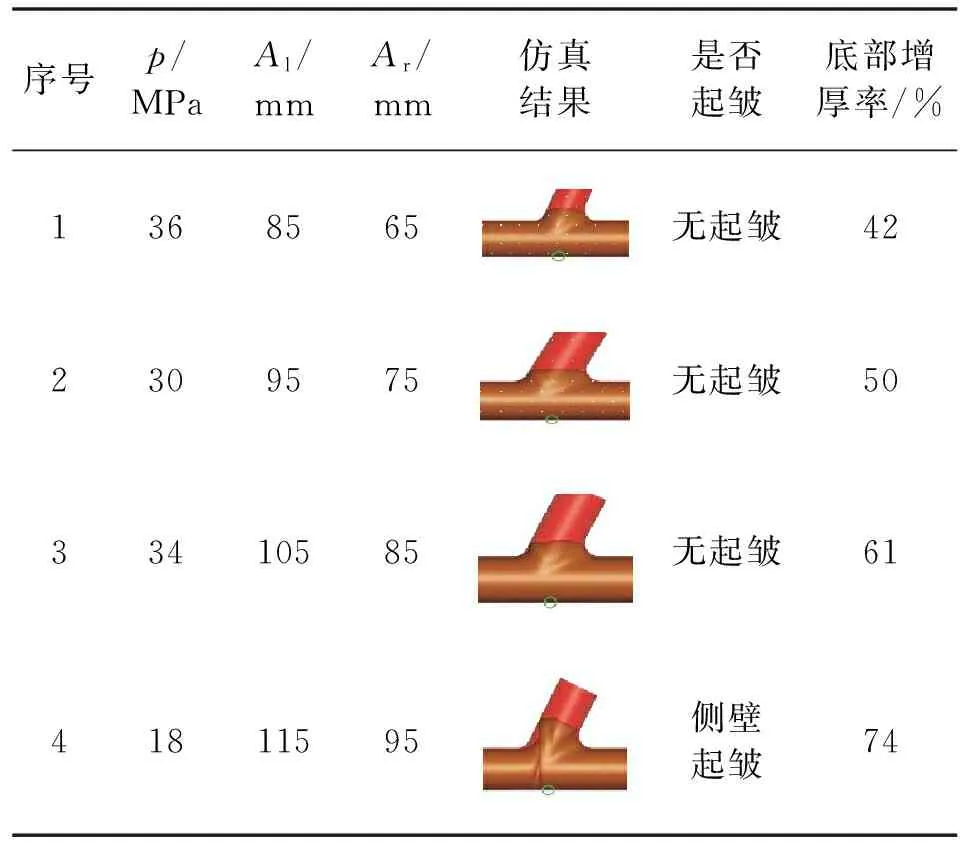
表4 第1阶段不同加载路径仿真结果

2.1.2 第2阶段模糊控制器设计

控制思路：当左间隙(左边圆角起皱间隙)过大时，减小左边轴向进给量，增大内压；右间隙的控制规则和左边相同，但变量的论域范围不同。第2阶段的模糊控制系统结构如图8所示。

图8 第2阶段模糊控制系统结构

采用Simulink仿真方法进行各变量的论域范围确定及模糊区间划分，如表5所示，共设计了16条模糊控制规则，如表6—表8所示。

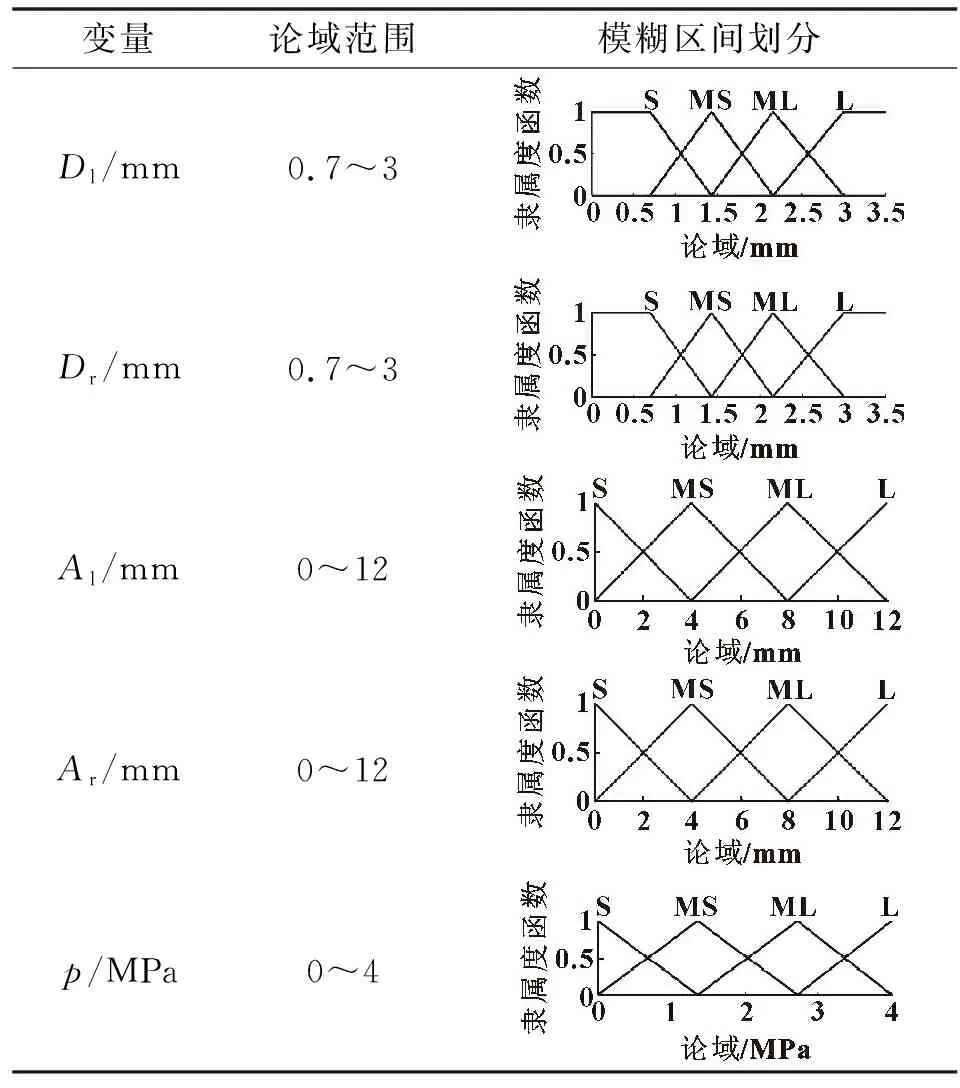
表5 变量论域范围确定与模糊区间划分

表6 第2阶段左冲头模糊进给量控制规则

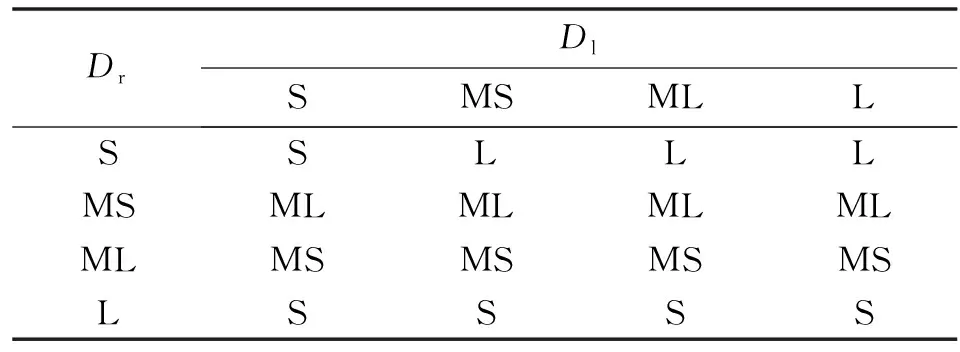
表7 第2阶段右冲头模糊进给量控制规则

表8 第2阶段压力增量模糊控制规则

2.1.3 第3阶段模糊控制器设计

在第3阶段，材料与左右圆角贴模接触，胀形顶部也与支管反推冲头接触。由于顶部与反推冲头的接触面为椭圆形，将左右圆角的起皱间隙(、)和顶部与反推冲头接触纵剖面中两边未贴模的长度(、)作为控制输入，如图9为第3阶段模糊控制系统结构。该阶段的模糊区间和模糊控制规则与第2阶段相似，论域范围为(0.7～3) mm、(0.7～3)mm、(0～10) mm、(0～4) mm、(0～3) MPa，共设计了16条模糊规则。

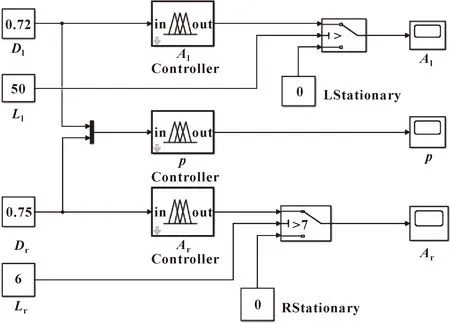
图9 第3阶段模糊控制系统结构

2.1.4 第4阶段模糊控制器设计

第4阶段为支管反推冲头开始移动至设定值。反推冲头位移为控制思路：如果未贴模长度过大且圆角起皱间隙很小，则轴向进给增量取大，内压增量取小。图10所示为模糊控制系统结构。该阶段的模糊区间和模糊控制规则与第2阶段相似，论域范围为(34～38) mm、(1～2.5) mm、(1～2.5) mm、(7～10) mm、(3～6) mm、(0～1.5) mm、(0～2.5) MPa、(0～8) mm、(0～5) mm，设计了16条模糊规则。

图10 第4阶段模糊控制系统结构

2.2 加载路径优化

将模糊控制系统优化的加载路径作为仿真参数的输入，图11所示为仿真结果。可知：最大减薄率为25.1%，比图3约增大了14%，最大增厚率减小了约2%，没有看到成形效果的显著改善。这是因为第1阶段采用了线性加载的方式，而线性加载的速率影响材料成形的最终减薄与增厚结果。由于第1阶段起皱的形式不一样，对成形的结果影响最大，因此对第1阶段模糊控制器进行重新设计。

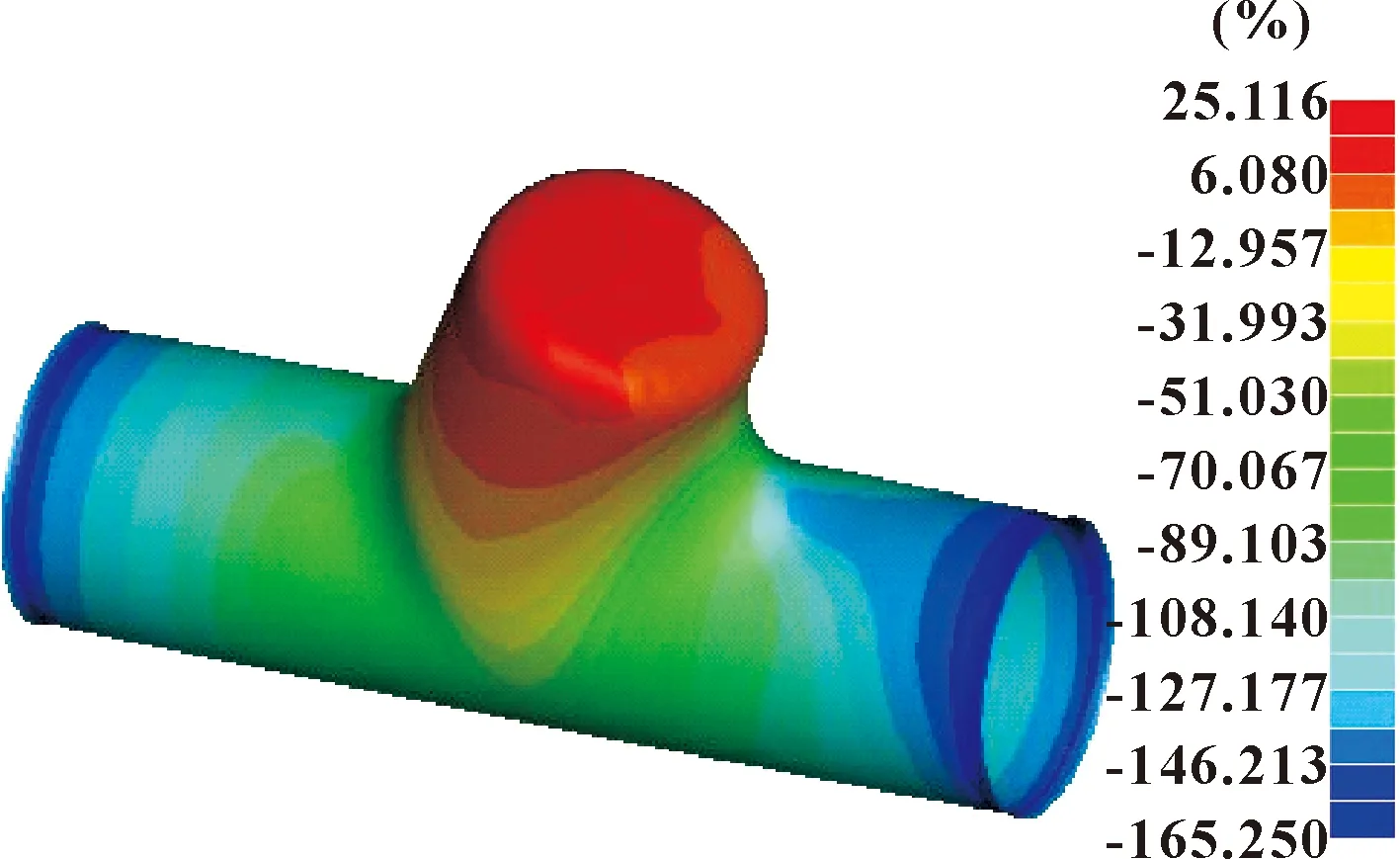
图11 优化后减薄率等值线

2.2.1 第1阶段线性加载速率对成形质量的影响

选取6种第1阶段轴向进给速率如表9所示，在内压加载速率和其余阶段模糊控制器不变的情况下进行加载。图12所示为特征点位置以及减薄率变化规律曲线。可知：随着第1阶段轴向进给速率增加，最大减薄率逐渐变小，底部区域的增厚率也逐渐增加；方案6的仿真结果与第1.1节仿真结果相比，在最大减薄率相近的情况下，最大增厚率降低了约2.6%，提高了壁厚分布的均匀性。

表9 第1阶段线性加载速率

图12 特征点及其减薄率变化曲线

2.2.2 第1阶段左右线性加载匹配对成形质量的影响

保证第1阶段进给总量一定，设计3组试验，保持内压线性加载速率恒定，左进给/右进给总量分别为42 mm/50 mm、46 mm/46 mm、50 mm/42 mm。图13所示为特征点减薄率变化规律曲线，可以发现：随着第1阶段左轴向进给总量增加，右边轴向进给总量减少，最大减薄率和底部中间增厚率变化不明显，但节点2、3之间的增厚率差值是递增的关系。另外，随着左进给/右进给的比值增大，减薄率有逐渐递减的趋势。因此，在第1阶段中调整左右轴向进给的配比，可以有效调节最终零件的厚度分布。

图13 特征点减薄率变化曲线

2.3 加载路径优化

当仅微小起皱时，需要增大内压将它压平，否则会出现死皱，进而起皱与开裂。表10、表11分别为第1阶段论域范围与模糊控制规则。

表10 第1阶段变量模糊区间划分

表11 第1阶段模糊控制规则

调整相应变量的论域范围即可达到很好的控制效果，最终得到优化的加载路径如图14所示，仿真结果如图15所示。与文献[10]中的试验结果对比如图16所示，优化后充模效果显著提升，验证了所构建的模糊控制系统优化加载路径的有效性。

图14 加载路径优化结果

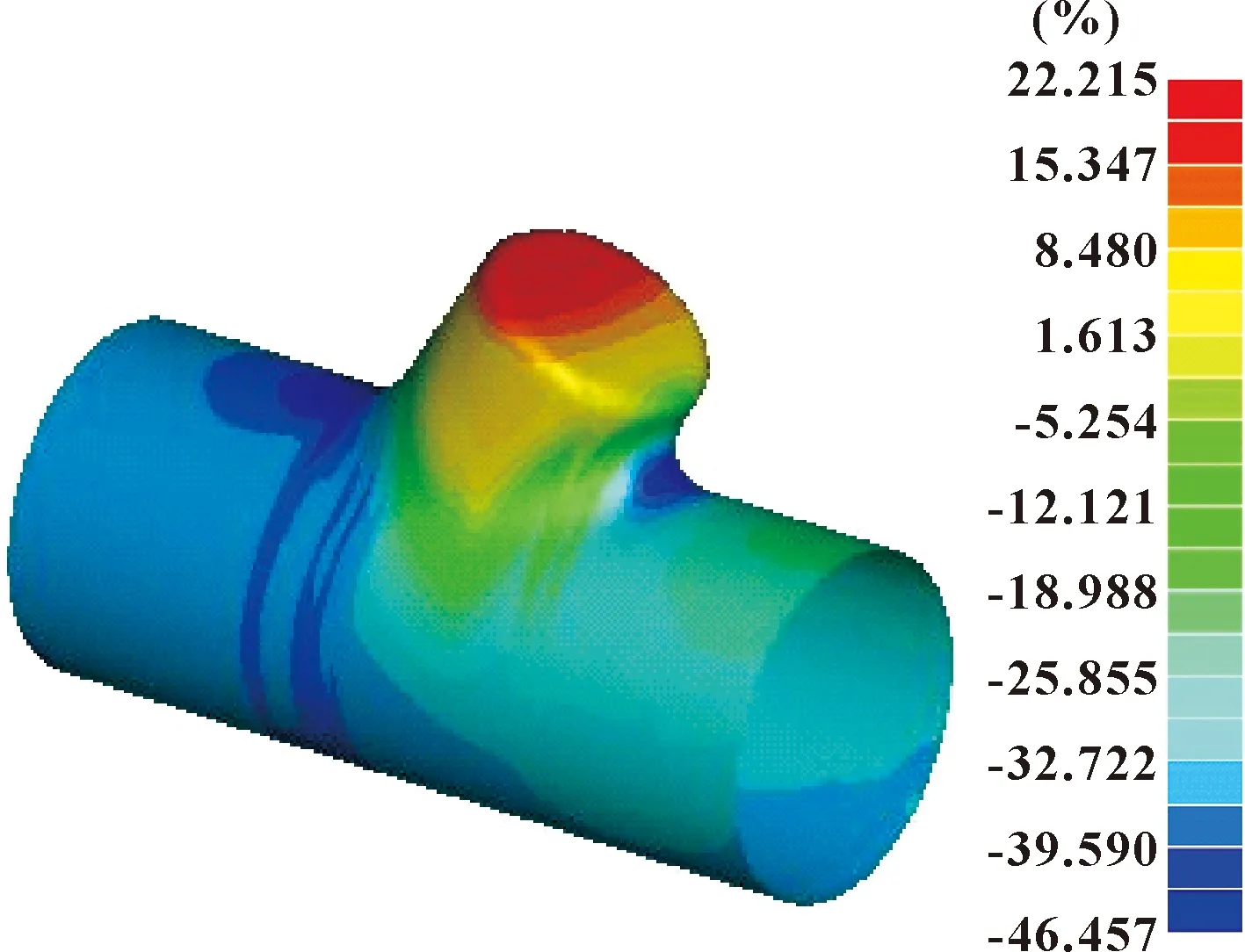
图15 优化后减薄率等值线图(最终)

图16 优化结果与试验结果对比

3 应用研究

3.1 Y形管结构改进与成形性分析

图17所示为某汽车排气系统Y形歧管零件原始模型，其原始加工工艺是先冲压后焊接。该零件左右两端口平面的法线方向为异面，需要经两次弯管工艺再进行内高压成形。在保证装配位置尺寸的情况下，对弯管结构进行改进。工艺成形困难的原因为两支管轴线为异面直线，将它改为相交直线即可变成共面，且增大弯管轴线弯曲半径为270 mm，可实现一次弯曲。

图17 Y形歧管零件原始模型

3.2 应用模糊控制系统优化加载路径

对第2.1节中各阶段模糊控制器稍作更改。由于结构的特殊性，第2阶段并不明显，因此省略第2阶段的控制过程，将其成形划分为3个阶段，将第2.1节中的第3、4阶段引入起皱间隙，作为更改后模型的第2、3阶段的模糊控制器输入。将起皱间隙的大小和有无作为控制轴向进给增量和内压增量的决策条件之一，同时在每一阶段加上底部起皱间隙作为控制输入。第1阶段的论域范围与模糊区间划分及在第2、3阶段变量的模糊区间划分如表12所示。新增对被控变量的控制规则如表13—表18所示。根据改进的模糊控制器进行加载路径优化，得到的优化结果如图18所示。胀形高度为39 mm，最大减薄率为14%，两端增厚较严重。由于端口工艺补充部分需要切除，而且下一步还需要进行胀口工序，两端增厚有助于缓解胀口工艺导致的材料减薄，因此认为是合理的。

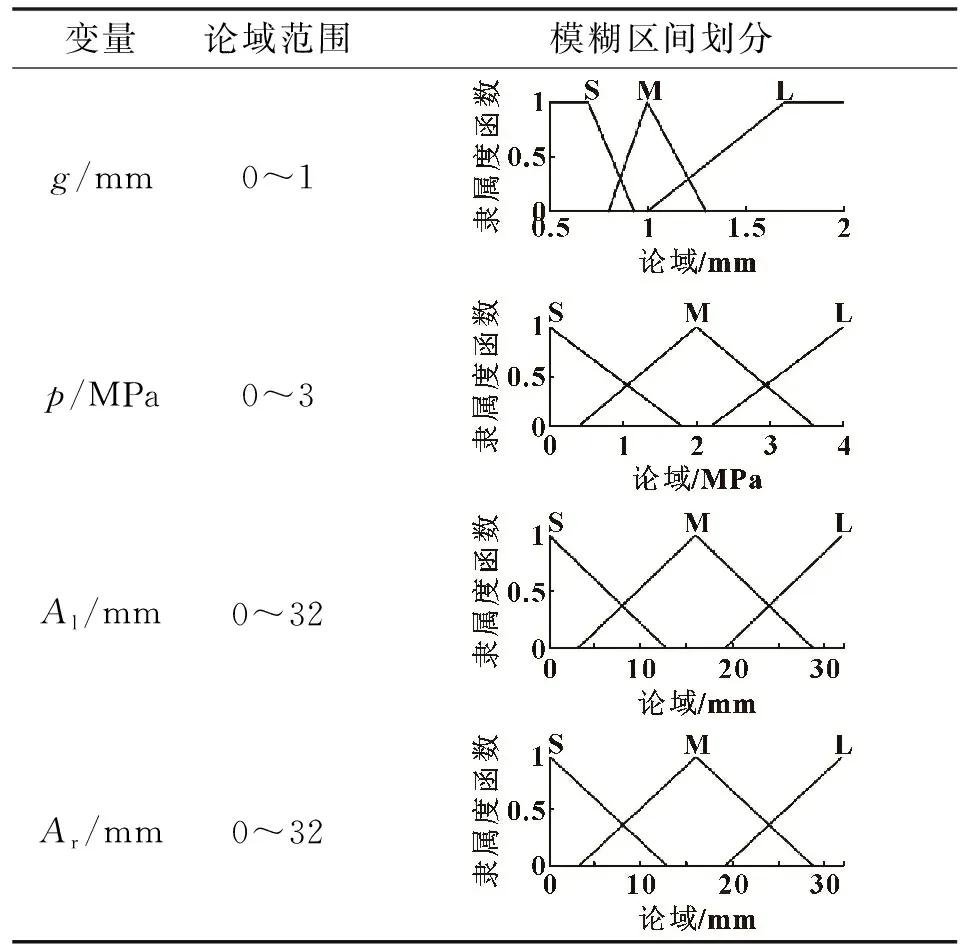
表12 某汽车排气系统Y形歧管第1阶段论域范围与模糊区间划分

表13 第2阶段新增控制规则(Al Controller)

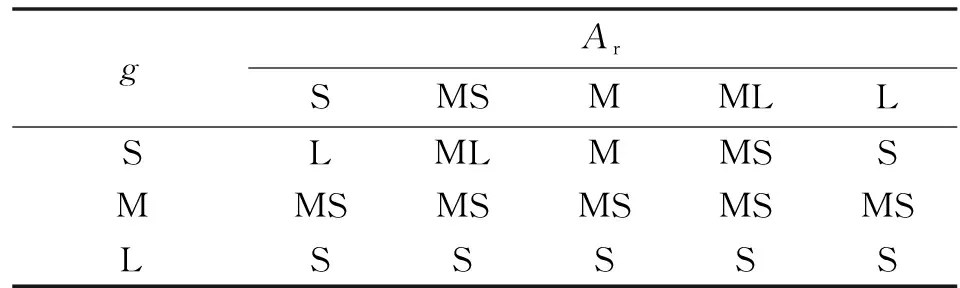
表14 第2阶段新增控制规则(Ar Controller)

表15 第2阶段新增控制规则(p Controller)

表16 第3阶段新增控制规则(Al Controller)

表17 第3阶段新增控制规则(Ar Controller)

表18 第3阶段新增控制规则(p Controller)

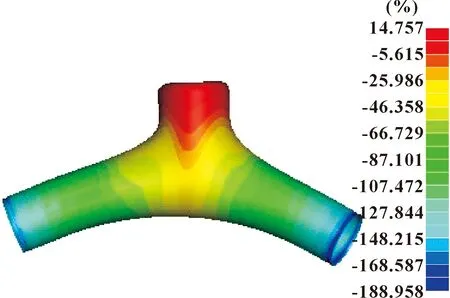
图18 某汽车排气系统Y形歧管优化后减薄率等值线

4 结论

(1)通过 Dynaform 软件建立了薄壁Y形管内高压成形的有限元仿真模型，分析了Y形管转角处圆角半径、摩擦因数和加载路径对成形质量的影响。

(2)按照成形过程特点，将Y形管分为4个阶段，选取起皱间隙和贴模长度作为逻辑控制输入，评价成形状态，建立模糊控制系统，优化Y形管内高压成形加载路径，优化后充模效果得到较大提升。

(3)通过改进某汽车排气系统Y形歧管零件的结构，将内高压成形工艺和所构建的模糊控制系统应用于此零件，实现了成形工艺的改进和加载路径的优化。

本文作者为内高压成形的加载路径优化提供了一种模糊控制器的设计方法，能够减少生产中调试工艺参数的次数并且得到更好的成形质量，为内高压成形零件的生产提供参考。