非连续边界荷载影响下隧道围岩压力计算方法

聂红宾， 谷拴成， 周志强， 张建鹏

(1. 陕西铁路工程职业技术学院城轨工程学院， 陕西 渭南 714000； 2. 西安科技大学建筑与土木工程学院，陕西 西安 710054； 3. 中铁第六勘察设计院集团有限公司， 天津 300308； 4. 山东省建筑科学研究院有限公司， 山东 济南 250031)

0 引言

在浅埋暗挖隧道施工中，堆载、孤石、起伏岩层引起的非连续荷载对隧道会产生一定的附加应力。在这种应力的影响下，围岩压力的取值与衬砌结构安全息息相关。在实际工程设计中，因压力设计偏差导致的工程事故时有发生[1]。

国内外学者对于围岩压力模型及计算方法进行了大量研究，主要采用工程实际类比、理论计算及原位测试方法。Laura等[2]、Moodie[3]对不同厚度板中圆孔压力进行分析，通过荷载传递建立了压力模型，被称为应力梯度理论。Houmat[4]利用应力梯度法揭示了连续均布边界荷载在高密度材质中的传递规律。研究发现，这种方法对小区域的材料适用，而对于大体积围岩，压力计算值偏差较大。因此，围岩压力计算最早采用全土柱理论，其不考虑边界荷载影响，而是将边界荷载以附加压力的形式与岩层压力值叠加，这就造成围岩压力随隧道埋深的增加而计算值偏大。俄国学者普罗托奇雅阔诺夫基于塌落拱提出了普氏理论[5]，认为拱以外的围岩可等效为连续边界荷载，其压力计算值与隧道埋深无关，而与等效连续边界荷载取值有关。太沙基认为岩体间有一定的黏聚力，根据上覆围岩破裂迹线，以应力传递为基础，建立了围岩压力计算模型[6]，但该理论认为岩体破裂滑移迹线为扩展垂直折线，地表边界条件直接假设为连续边界荷载。比尔鲍曼认为全土柱理论计算值偏大的原因是未考虑土柱两侧边界的摩擦力和黏聚力，据此建立了比尔鲍曼围岩压力计算理论[7]，但仍然采用了全土柱垂直滑移迹线。谢家烋[8]采用的滑移迹线与全土柱、太沙基理论不同，其认为滑移迹线是一条与水平线成β角的斜直破裂线，同时将上覆围岩分为3部分，通过3个楔形体之间相互几何关系建立围岩压力。通过上述分析可知，谢家烋理论采用斜直线表示滑移迹线更加符合浅埋隧道破坏规律，但该理论将楔形体分为3部分，仅考虑中间部分荷载作用，两边三角形体对中间土柱仅提供支撑作用，未考虑边界条件影响。20世纪以来，学者普遍认为： 因隧道开挖扰动，上覆岩体会存在节理裂隙等内部缺陷。Shanley等[9]、汪小刚等[10]认为隧道围岩缺陷服从Bingham分布，分别提出负指数分布、正态分布和对数分布等破坏滑移模型。根据试验数理统计和理论验证，浅埋隧道上覆岩体破坏滑移线是沿隧道侧壁斜向上直至地表，谢家烋模型更加符合实际。

上述围岩压力计算的前提条件是边界荷载连续或者不考虑其影响。但在实际工程中，大部分边界荷载并不连续。皮亮等[11]、蔡鑫等[12]以原位测试方法研究了高层建筑、孤石等附加荷载对隧道围岩压力的影响。吴红刚等[13]、童建军等[14]将飞机、滑坡体按照集中荷载考虑，以集中荷载在半无限空间应力分布计算方法得到附加应力，并与围岩压力值叠加组合，形成集中边界荷载影响下围岩压力分算理论； 魏纲等[15]以明德林公式(以集中荷载应力法为基础)推导了基坑卸荷对既有地铁隧道的应力影响；上述研究利用压力分算较好地解决了非连续荷载对围岩压力的影响，但该理论没有考虑边界荷载在岩体的应力扩散问题，且未对边界荷载进行模型划分及选取。因此，对于隧道进出口浅埋地段的堆载、大型孤石的压力验算，将其认为集中荷载还是均布荷载没有定论，相关规范也未做出明确规定。

针对浅埋暗挖隧道，本文以拉林铁路隧道群为项目依托，按照非连续荷载作用形式、位置及其随地层深度传递限值分为不同工况，基于隧道围岩破坏理论建立压力模型，根据太沙基应力传递理论及弯矩在半无限空间体产生的附加应力，得到不同工况围岩压力方程，最后根据拉林铁路的实际情况对围岩压力进行分析，验证模型的可行性，以合理优化隧道线路。

1 模型建立

1.1 基本假定

为了满足不同工况影响下围岩压力计算需求，进行以下假设：

1)围岩完整或者节理、裂隙均匀分布，具备连续积分条件；

2)围岩发生破坏时，破坏楔形岩体与原岩完全脱离，在塑性滑移线处仅存在支撑力和摩擦力；

3)围岩分布均匀，不考虑岩体间物理力学性质差异；

4)楔形岩体属于半无限大空间体。

1.2 不同工况作用下围岩压力模型确定

围岩压力计算模型如图1所示。按非连续边界在地表作用范围，将边界分为集中荷载和均布荷载，按荷载距隧道中线作用位置，可分为工况1和工况2。当边界荷载分布在楔形体Ⅱ时为工况1， 此时隧道受到偏压荷载作用；当边界荷载分布在楔形体Ⅰ上且对称分布在y轴两侧时为工况2，称为轴对称受压工况。根据大量浅埋隧道破坏试验可知，岩体的破坏滑移线主要有指数、抛物线、直线等类型，为了简化计算，采用直线破裂滑移线建立受力模型(见图1)。

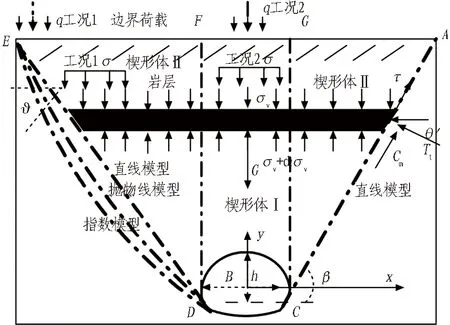
q为地表荷载； σv为土条上部的围岩压力； ϑ为附加荷载在岩层中的应力扩散角； σ为边界荷载在岩体形成的附加应力； G为土条重力； τ为土条斜边剪应力； Cm为破坏岩体与原岩间的摩擦力； Tt为原岩对破坏岩体的推力； θ′为原岩对土条斜边角度； B为隧道宽度； h为隧道高度； β为隧道开挖岩体破裂滑移线与x轴夹角。图1 围岩压力计算模型Fig. 1 Calculation model of surrounding rock pressure

2 边界确定

2.1 地表非连续边界确定

当边界荷载处于轴对称工况时，其在岩体任一深度处会产生相应的附加应力，应力有效分布长度随隧道埋深增加。围岩压力按非连续边界考虑，有效分布长度应满足式(1)； 否则，按连续边界考虑。

(1)

式中：l为边界荷载随岩层深度分布的有效长度；hm为隧道埋深；y为边界荷载距附加应力作用位置的距离。

边界荷载随隧道深度扩散按照《建筑地基基础设计规范》[16]考虑，

l=b+2ycot ϑ。

(2)

式中b为地表非连续边界荷载的分布宽度。

将式(1)和式(2)联立后，可得到非连续边界荷载作用下地层计算深度临界值，见式(3)。

(3)

2.2 围岩滑移边界确定

在图1中，岩体破裂滑移直线模型参考陈松[17]求解方法，在隧道中心建立坐标系，破裂点A、C坐标分别为(X/2，h)、(R/2，0)，则滑移线方程为

(4)

将方程改写为变量y的函数，

f(y)=y-。

(5)

对式(5)求导，导数

(6)

3 围岩压力计算

3.1 轴对称工况围岩压力计算

以边界条件为均布荷载计算围岩压力，按照图1所示，取围岩任意段进行研究。

垂直方向平衡方程为

qb+f(y)σv+γf(y)dy-(σv+dσv)f(y+dy)-Fhdy=0 。

(7)

式中Fh为任意段dy侧边竖向合力。

岩体侧面滑移位置摩擦力与推力关系如图2所示。

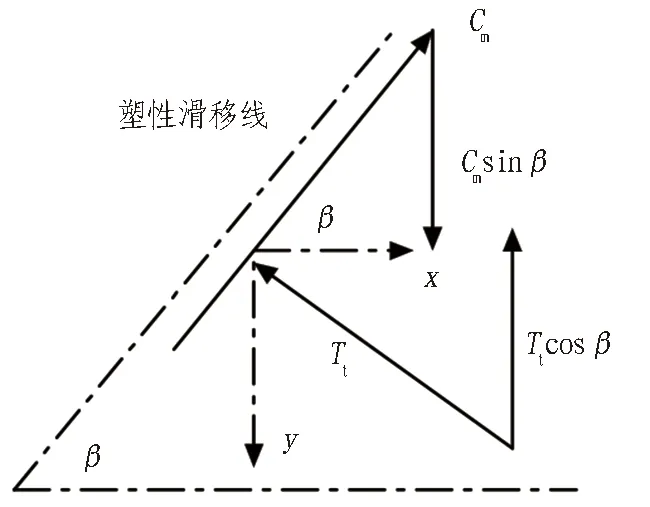
图2 岩体侧面滑移位置摩擦力与推力关系Fig. 2 Friction and thrust relationship on slip line

由图 2，

Fh=Ttcosβ-Cmsinβ。

(8)

原岩沿破裂线对破坏岩体的推力

(9)

式中γ为隧道围岩重度。

摩擦力

(10)

式中：C为黏聚力；λ为侧压力系数；φ为岩体内摩擦角。

联立式(7)—(10)，可得

(11)

将函数f(y+dy)展成泰勒级数，

f(y+dy)=f(y)+f′(y)dy。

(12)

将式(12)代入式(11)中，整理后可得到

(13)

将式(5)和式(6)代入式(13)，得到

(14)

整合式(14)，令分子为0，两边除以dy，不考虑二阶效应影响，进行积分，得到

(15)

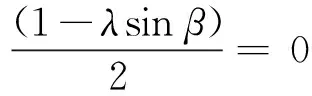
(16)

非连续边界荷载条件为

(17)

(18)

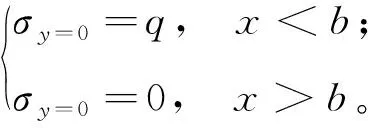
(19)

按照式(19)，边界条件为非连续函数，无法直接积分，但边界荷载总和为qb，据此可得到

(20)

将式(20)中y按照式(5)换成x函数，经过积分变化后解得

(21)

将式(21)代入式(16)和式(18)中，可得到轴对称非连续均布边界荷载影响下的围岩压力。

3.2 偏压工况围岩压力计算

在图1的2种工况作用下，当偏压工况1的边界荷载移动到轴对称工况2相应的位置时，会产生附加弯矩Mf。因此，可将偏压工况的非连续边界荷载等效为轴对称工况等值荷载作用，其产生的压力与附加弯矩形成的应力组合可得到偏压工况围岩压力。设非连续边界荷载到y轴的距离为d，则附加弯矩

(22)

按照卜万奎等[18]的算法，在岩体半无限空间中，弯矩作用下形成的附加应力为：

(23)

式中：r为半无限空间体作用下的极坐标半径；I为应力复变函数系数；θ为弯矩方向从右向左的转角；ai为应力函数系数，i取值1、2、3。

在地表处，假设岩体半径无限大时，切向应力与剪切应力为0，在垂直方向径向应力为等效边界荷载作用，将其用函数表示为

(24)

将式(24)代入式(23)，解得待求参数

(25)

将式(25)代入式(23)，则弯矩作用下岩体附加压力为

(26)

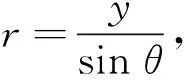
(27)

式中σh为弯矩形成的水平方向围岩压力。

将式(22)代入式(27)后，与轴对称等效工况围岩压力进行组合，可得到偏压工况围岩压力计算方法：

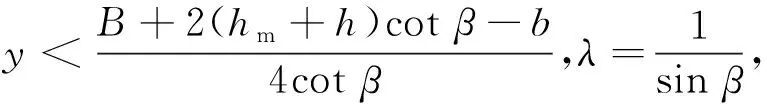
(28)

(29)

(30)

式中σvf为附加弯矩Mf产生的竖向围岩压力。

3.3 集中边界荷载影响下围岩压力计算

当非连续边界为集中荷载作用时，仍将岩体等效为连续半无限空间体，围岩压力可按照符拉芒解答考虑，将应力经过坐标转换后，集中荷载影响下围岩附加应力为

(31)

式中：B-1为球坐标与直角坐标转换矩阵的逆矩阵；P为集中荷载。

集中边界荷载按照此规律向围岩传播，围岩压力计算办法与均布荷载类似，唯一不同的是边界荷载形式，本文不再赘述。

4 围岩压力分析

4.1 围岩压力监测

以拉林铁路隧道群为研究对象，隧道地表存在孤石，位于隧道浅埋出口段，其高度为9 m、宽度为0.5 m、长度为0.4 m，洞口段埋深暂定为5 m，孤石到洞身中轴线的距离为7 m。隧道采用全断面预留核心土法施工，在隧道内布设ZKYLJ-20钢弦式压力盒进行围岩压力监测，分别布设在拱顶、拱肩及侧墙，共设置5个监测点。按照监测规程要求，围岩压力监测如图3所示。经过数据残差处理后，围岩压力变化如图4所示。

(a)

(b)图3 围岩压力监测Fig. 3 Monitoring of surrounding rock pressure

图4 围岩压力变化Fig. 4 Monitoring values of surrounding rock pressure

由图4可知，在孤石荷载影响下，拱顶与拱肩1处围岩压力较大，但在隧道开挖17 d后围岩压力不再增大，说明隧道趋于稳定，支护发挥了作用。

4.2 围岩压力计算

孤石属于大理石岩，均匀无倾角，重度取27 kN/m3，隧道围岩重度为17.0～18.3 kN/m3，直接取18 kN/m3，黏聚力C取30 kPa，内摩擦角φ为27°。侧压力系数λ取值0.414时，隧道设计埋深为5 m。按照式(3)计算非连续边界荷载临界值为12.2 m，该隧道设计埋深小于临界计算值，按照非连续偏压荷载边界考虑。

1)先将孤石按照均布荷载考虑，则隧道边界非连续均布荷载

q=27 kN/m3×9 m×0.5 m=121.5 kN/m 。

(32)

非连续边界对隧道形成的附加弯矩

(33)

按照陈松[17]的拟合，破裂滑移线函数中R与X的关系为

(34)

经计算，R、X分别取值-94.630、-88.633。

破裂面函数中，

(35)

(36)

σv=261.664-44.198sin 2θ(cos 2θ+1)cosθ。

(37)

2)将孤石按照集中荷载考虑时，集中荷载取值48.6 kN，附加应力按照式(31)计算，围岩压力

σv=251.952-(3.094-4.332sin 2θ)(cos 2θ+1)·cosθ。

(38)

按照式(37)和式(38)，可得到非连续边界荷载影响下围岩压力计算值。

4.3 围岩压力对比

将围岩压力计算值与监测值进行对比，结果见图5。由图可知： 将孤石等效为均布荷载时，隧道衬砌不同位置角度对围岩压力影响较大，而对集中荷载形成的压力影响较小。这表明不论采用何种模型计算，围岩压力均受衬砌位置角度影响。2种模型计算的围岩压力值与监测值之间存在一定的误差，若以监测值为准，2种模型的围岩压力差沿隧道衬砌不同位置的变化见图6。

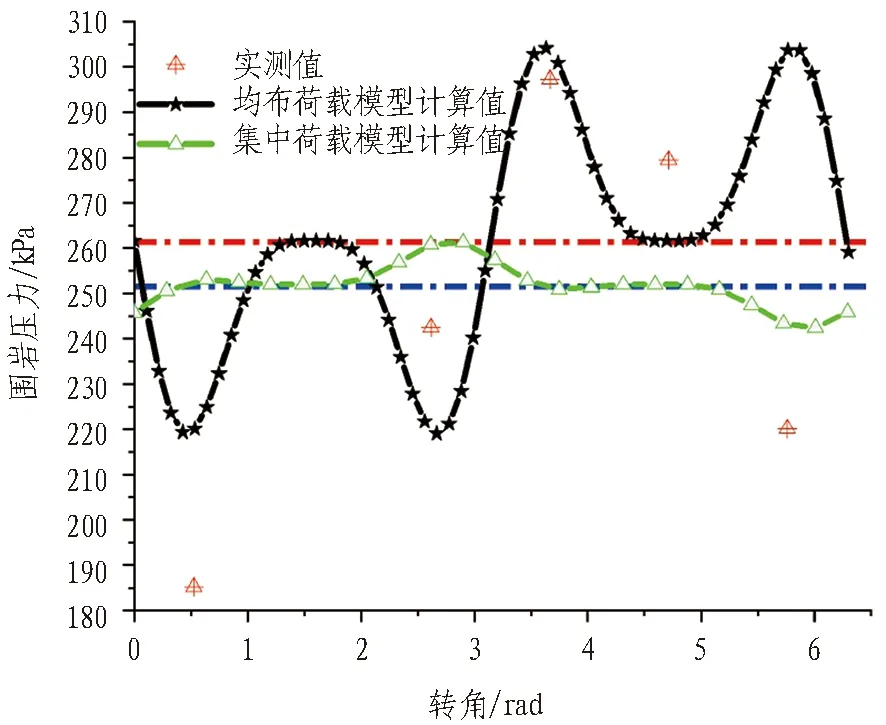
图5 围岩压力计算值与监测值对比Fig. 5 Comparison between calculated and monitored values of surrounding rock pressure

图6 围岩压力差分布Fig. 6 Analysis of surrounding rock pressure error

由图6可知，集中边界荷载的围岩压力差较大，且数据分散；而均布荷载的压力差较为均匀，与衬砌位置角度呈线性变化。通过图5和图6中压力值与误差分析可知，当隧道埋深设计为5 m时，将非连续边界假定为均布荷载模型较为适合。

为了优化隧道线路，采用不同理论进行围岩压力计算(全土柱理论和规范法[19]计算围岩压力时，孤石作为固定围岩压力考虑)，得到围岩压力与隧道埋深关系如图7所示。由图可知： 1)全土柱理论围岩压力计算值明显偏大，不适用于该隧道的压力计算。2)规范法对其进行改进后，明显与实际相符，但随着埋深增加，压力计算值始终大于监测值。3)本文提出的围岩压力计算方法较为接近监测值，隧道埋深对边界荷载的假定有一定影响； 当埋深小于7 m时，将孤石作为非连续均布荷载的围岩压力计算值与监测值相近；当埋深大于8 m时，将孤石作为非连续集中荷载的围岩压力计算值与监测值较为接近。

图7 不同算法围岩压力与隧道埋深关系Fig. 7 Relationship between surrounding rock pressure and buried depth in differential analysis methods

5 结论与建议

1)边界荷载在岩体扩散的有效长度可作为围岩压力计算方法选取依据。边界荷载有效扩散长度随隧道埋深增加，当分布长度大于围岩压力荷载计算宽度时，可按照均布边界条件计算围岩压力，否则，按非连续边界考虑。

2)围岩压力取值与隧道衬砌位置有关。通过拉林铁路隧道群工程实际对围岩压力方程进行参数化处理，将计算值与监测值对比可知，非连续边界荷载影响下围岩压力计算值受隧道衬砌位置角度影响，且压力差与角度呈线性关联。

3)通过不同理论对围岩压力计算发现： 非连续边界模型选取与隧道埋深有关，本文提出的围岩压力计算方法较为接近监测值。当埋深小于7 m时，建议将边界条件等效为均布荷载；当埋深大于8 m时，建议将边界条件等效为集中荷载。

非连续边界荷载是隧道进、出口段主要危险源，本文假设围岩均质、连续可积，但实际工程中围岩常是层状破裂岩体，造成围岩压力的理论与实际难于完全匹配，但通过不同围岩压力的理论计算，本模型较为接近实际监测值，有较高的精确度，建议下一步研究岩层、节理对围岩压力取值的影响。