束合管幕结构结合缝压弯性能足尺试验研究
毕湘利, 王秀志, 张中杰, 潘伟强, 焦伯昌, 柳 献, *
(1. 上海申通地铁集团有限公司, 上海 201102; 2. 上海市城市建设设计研究总院(集团)有限公司, 上海 200125; 3. 上海隧道工程有限公司, 上海 200032; 4. 同济大学地下建筑与工程系, 上海 200092)
0 引言
在软土地区,暗挖法因其具有对环境影响小等特点,逐渐成为中心城区地下建筑施工的首选方案。常见暗挖法包括顶管法、盾构法、管幕法、冻结法等,不同的工法均有其特点以及相应的适用性。对于尺寸超大、距离较短、形状不规则的地下工程,管幕工法就成为了施工的最佳选择。
初期的管幕结构多采用圆形钢管,钢管之间不能协同工作且仅为单向受力,支护效率较差,且管幕结构仅作为施工阶段的临时支撑使用,不作为永久结构,因此钢管利用率低,成本较高。在后来的工程实践中,逐渐发展出了管幕-箱涵法[1],管幕结构开始作为永久性支护结构使用。近些年来,又逐渐发展出了以环梁为连接方式的NTR工法[2]、以翼缘板螺栓连接为连接方式的STS工法[3]、以无黏结预应力为连接手段的PCR工法[4],还开发了新型JES接头的JES工法[5-6]等新型管幕工法,逐渐减小了构件尺寸并提高了管幕结构的整体刚度和承载能力。
基于新型管幕工法的施工方式及结构特点,目前国内外的研究主要分为2个方面: 一方面是研究管幕法施工过程中的环境影响、地面沉降和开挖面稳定性[7-9]; 另一方面则是针对管幕的结构刚度、受力性能及破坏模式等进行研究[10-11]。NTR、STS、FCSR等新型管幕工法基本上通过强化钢管间连接、采用翼缘板与螺栓或环梁连接等方式,将钢管节连接成整体,进而提供管幕横向结构刚度及承载能力。PCR工法及日本URT工法的根本原理则是通过施加横向无黏结预应力来约束管节,进而提高整体结构的受力性能; 国内基于该原理提出了新型束合管幕工法(underground bundled integrate tunnel, U-BIT),其工法介绍及施工流程可参阅文献[12]。U-BIT工法的创新点在于采用矩形管幕作为支护结构,管幕通过锁扣以及填充混凝土进行连接,并通过张拉横向预应力使各个钢管之间协同受力,形成受力整体,进而提高整体结构的受力性能。
为确保该结构的施工安全性,以及拓展该结构的适用性,有必要对其受力机制进行系列试验研究,了解结构的薄弱部位和影响结构承载能力的主要因素,为武定路束合管幕结构的设计、施工及运营监护提供试验依据,也为后续将束合管幕工法应用于大跨度暗挖车站提供理论基础。
1 工程概况
国内首例U-BIT束合管幕工法应用于上海轨道交通14号线武定路站1号出入口,如图1所示。该管幕隧道埋深4 m、长8.4 m、高6.2 m,角部采用4个外延尺寸1.4 m×1.4 m的工作管,用于张拉及锚固预应力筋,顶底及侧部采用外延尺寸1.0 m×1.0 m的工作管,共16个,管节间隙宽0.1 m。

图1 束合管幕施工Fig. 1 Construction site of bundled integrate tunnel
2 试验设计
本文主要针对束合管幕结构结合缝压弯性能进行足尺试验,测试结合缝承受正负弯矩的受力特性与承载能力,研究结合缝的转角刚度值与极限承载能力,并探究角部结合缝受力全过程的性能发展规律与力学机制。
2.1 试验试件
从整体束合结构中截取3个管节进行压弯试验,采用的管节分为2类: 一类是外延尺寸为1.4 m×1.4 m的工作管; 一类是外沿尺寸为1 m×1 m的标准管。管节上下处分别有钢锁扣,根据其形态又分为C型锁扣和T型锁扣,锁扣厚度为20 mm,沿管节纵向长度1.5 m,钢材均为Q345B钢。在钢管节纵向方向,间距500 mm设置1个波纹管,内穿3根钢绞线。在钢管节对应位置开孔(φ78 mm)用以内穿波纹管。束合管幕结构及试验管节如图2所示。
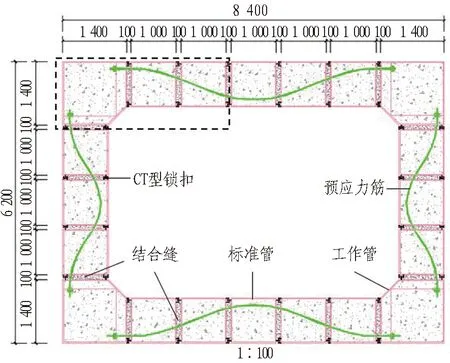
(a) 束合管幕结构

(b) 试验管节图2 束合管幕结构及试验管节(单位: mm)Fig. 2 Bundled integrate structure and test specimen (unit: mm)
2.2 加载系统
试验设计如图3所示(以负弯矩压弯力学性能试验为例),主要由反力框架、加荷千斤顶、加载梁及试件组成。竖向千斤顶固定于反力框架上,通过放置加载梁,将千斤顶的集中荷载转化为面荷载作用于结构之上; 反力框架则通过自身平面内受力平衡,为千斤顶提供反力作用。

图3 试验设计Fig. 3 Test design
正、负弯矩压弯力学性能试验所用管节尺寸均相同,仅在加载过程中将构件倒置,从而实现正负弯矩倒转的效果。
2.3 加载设计
压弯力学性能试验主要对结合缝压弯力学性能进行试验研究,利用上述加载系统进行加载。加载设计的原则是让试验中结合缝所受到的弯矩和轴力与整体结构中结合缝所受到的弯矩和轴力最不利荷载组合相同,并且逐渐加载使得结合缝出现破坏。
结合加载条件与试验目的,将整个加载工况分为设计工况、预应力+水平顶力+弯矩复合受力工况和9/6/3根预应力筋+弯矩复合受力工况,如表1所示。
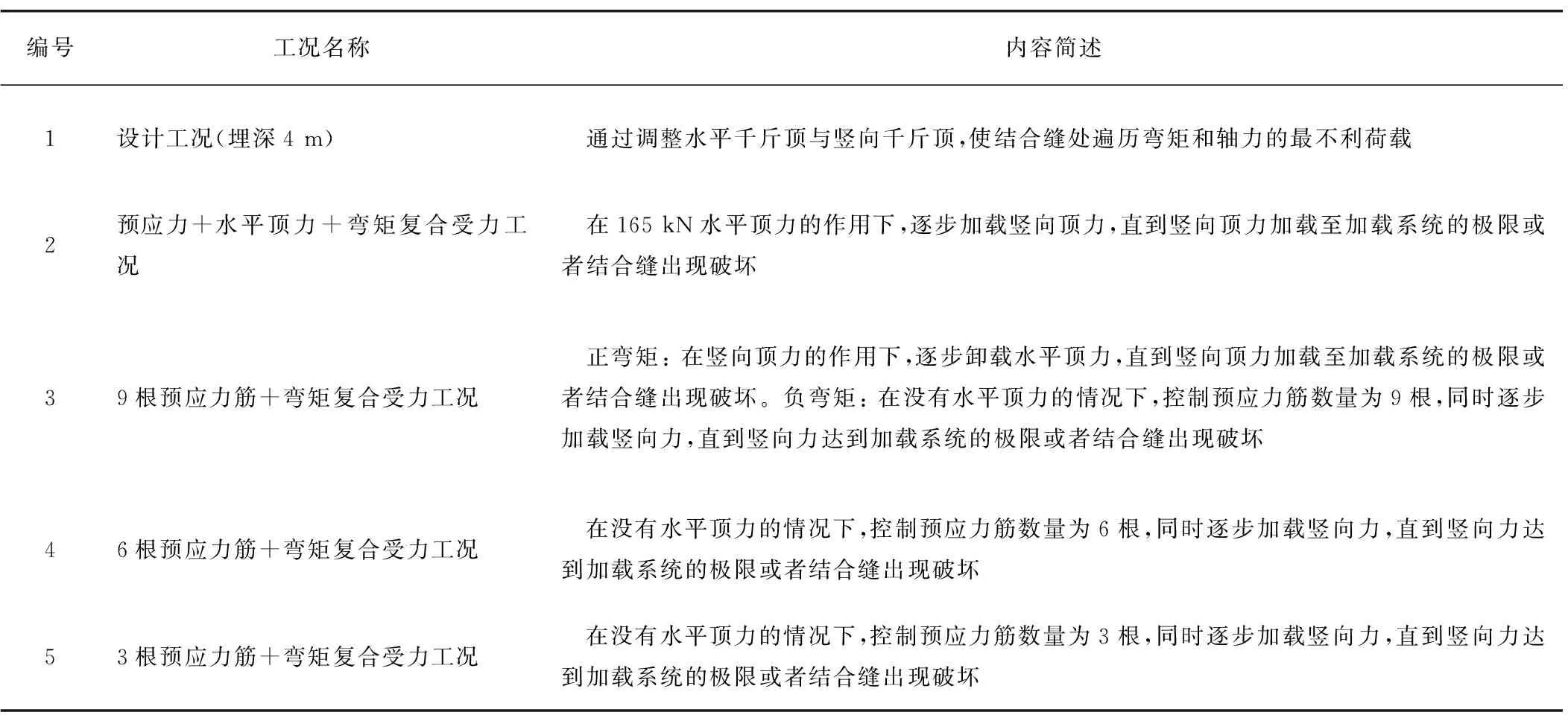
表1 压弯力学性能试验加载说明表Table 1 Loading description of mechanical properties of bending moment test
预应力筋采用1×7标准型钢绞线,公称截面面积为140 mm2。按照设计要求,预应力筋需张拉至极限应力的75%(即1 395 MPa),单根预应力筋设计张拉力为146.475 kN,单束预应力筋设计张拉力为439.425 kN。
2.4 监测内容
本次结合缝力学性能试验的主要测试内容有结构变形、结合缝张开、结合缝错台、管节应变、结合缝应变、预应力筋应变以及结构现象及过程记录。
为了达到研究目的,结合结构特点以及荷载形式进行有针对性的测点布置。在重要截面适当加密,并根据预分析计算结果,选取恰当的测试仪器。具体测试内容与方法如下。
1)结构变形。构件挠度测量传感器选用量程、精度恰当的拉线式位移传感器。将传感器一端固定在地面,并在管节自由端底部设置对应构件,为拉线提供条件,用于测量端部竖直向下位移。单组压弯试验在管节两端各布置3个挠度测点,如图4所示。

图4 结构变形测点布置Fig. 4 Arrangement of structure deformation measurement point
2)结合缝张开。选取电子位移传感器测量结合缝两侧钢管节的相对张开位移,量程50 mm,精度0.01 mm。在结合缝一侧的管节端面上用万向磁性支架固定,用位移计顶针水平顶在结合缝另一侧管节端面的钢支板上进行测量,测点布置如图5所示。

图5 结合缝张开测点布置Fig. 5 Arrangement of joint opening measurement point
3)结合缝错动。选取电子位移传感器测量结合缝两侧钢管节的相对错动位移,量程50 mm,精度0.01 mm。在结合缝一侧的管节端面上用万向磁性支架固定,用位移计顶针垂直顶在结合缝另一侧管节端面上进行测量,测点布置如图6所示。

图6 结合缝错动测点布置Fig. 6 Arrangement of joint dislocation measurement point arrangement
4)管节应变。在各管节前后端面距各管节边缘100 mm轴线处沿高度方向间隔200 mm布置应变片,单侧端面布置20个测点。同时,在管节前端面接缝处的钢板中心线上沿高度方向间隔200 mm布置钢板应变片,用于测量钢板横向应变,单侧面共布置20个应变测点,如图7所示。
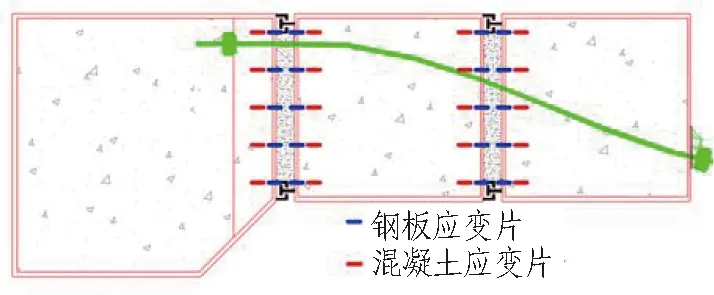
图7 管节应变测点布置Fig. 7 Arrangement of strain of pipe measurement point
5)结合缝应变。在管节结合缝锁扣上布置应变片进行应变测量。同时,在结合缝处利用混凝应变片测量试验过程中的结合缝混凝土应力变化,其布置在结合缝前后端面的中心轴线处,沿高度间隔150 mm进行布置,每个结合缝前后端面各布置5个应变花测点,一组试验共布置20个结合缝混凝土应变花测点,如图8所示。
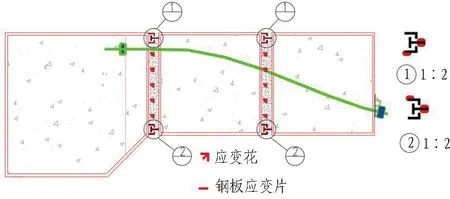
图8 结合缝应变测点布置Fig. 8 Arrangement of strain of joint measurement point
6)预应力筋应变。根据预应力筋线型与受力情况,在每根钢绞线的多个截面上粘贴箔式应变计,型号为BX120-1AA。在每个截面上粘贴2个应变片,截面的应变值取2个应变片所测定应变的平均值。
试验过程中,专人进行试验现象记录,包括试验全过程中结构整体变形与结合缝裂缝发展,以反映试验成果并作为验证的有力凭证。
3 主要试验结果
3.1 结合缝张开
3.1.1 正弯矩压弯试验
试验中,通过结合缝上下部位的张开变化量可以得到结合缝的转角值φ,即:
φ=(a-b)/h。
(1)
式中:a为结合缝上部张开量;b为结合缝下部闭合量;h为结合缝高度,取管节高度1 000 mm。
正弯矩工况1加载阶段,结构挠度、错台及张开均无明显变化。
正弯矩工况2、4加载阶段结构转角随弯矩的变化关系曲线如图9所示(工况3无弯矩变化)。

图9 正弯矩试验结构转角-弯矩关系曲线Fig. 9 Relation curves between rotation angle and bending moment of positive bending moment test
在正弯矩工况2加载阶段,加载初期结构转角无明显变化,转角刚度趋于无穷大。随着荷载继续增大,结合缝混凝土与钢管节发生脱开,表观上无脱开裂缝,而内部预应力筋应变陡增,反映内部已经出现脱开,预应力筋开始承受拉力。此时临界弯矩为489 kN·m,偏心距为0.264 m。随荷载继续增加,弯矩达到700 kN·m,结合缝混凝土与钢接触界面表观脱开,如图10所示。由结合缝单边脱开发展为双边脱开,结构进入非线性阶段,结合缝转角刚度降低至382 442 kN·m/rad,结构转角迅速增大至0.000 3 rad。随着荷载继续增加,脱开高度逐步增加,混凝土受压区高度逐渐降低,结合缝转角刚度降低。当弯矩低于930 kN·m时,转角刚度约为64 777 kN·m/rad,转角增至0.005 3 rad。随荷载进一步增加,混凝土受压区高度不再降低,而在剪力与轴力的共同作用下,结合缝底部混凝土出现斜裂缝,结合缝转角刚度进一步降低,此时转角刚度约为22 651 kN·m/rad,转角增至0.011 rad,如图11所示。

图10 结合缝脱开Fig. 10 Joint opening

图11 裂缝发展Fig. 11 Crack propagation
在正弯矩工况3加载阶段,保持竖向千斤顶顶力400 kN不变,逐步降低水平千斤顶顶力。当水平顶力卸载至275 kN,工作管结合缝上部的锁扣接触上。
在正弯矩工况4加载阶段,结构不受到水平千斤顶作用,同时预应力筋减少至6根。此时结构结合缝已经脱开,因此加载初期,结合缝就迅速张开,转角刚度约为64 608 kN·m/rad,转角增至0.014 rad。随着荷载进一步增加,结合缝张开继续增大,结合缝上部CT型锁扣接触受力。受到CT型锁扣的限制,结合缝无法继续张开,结构转角发展受限,反映为结合缝转角刚度迅速增大,转角刚度增大为314 880 kN·m/rad,转角增至0.014 6 rad。随着荷载继续增大,CT型锁扣受力增大,直至CT型锁扣无法继续承载外荷载,锁扣脱开,此时结构达到承载力极限状态。结合缝上部没有继续承担拉力的部分,张开量与转角迅速增大,绕着底部锁扣位置转动并向下塌落,结构发生破坏。该阶段转角刚度仅有7 742 kN·m/rad,转角增至0.023 rad。
3.1.2 负弯矩压弯试验
负弯矩工况1、2加载阶段,结构挠度、错台及张开均无明显变化。
负弯矩工况3—5加载阶段结构转角随弯矩的变化关系曲线如图12所示。

图12 负弯矩试验结构转角-弯矩关系曲线Fig. 12 Relation curves between rotation angle and bending moment of negative bending moment test
在负弯矩工况3加载阶段,初期加载时,结构转角无明显变化。结构在9根预应力筋的作用下,结合缝混凝土与钢管节发生脱开的临界弯矩为411 kN·m。在此之前结构基本无转角变化,转角刚度趋于无穷大。弯矩达到540 kN·m时,表观界面脱开。随荷载继续增加,结合缝转角刚度降低至200 000 kN·m/rad,结构转角迅速增大至0.001 5 rad。
在负弯矩工况4加载阶段,当外荷载产生的弯矩小于42 kN·m时,该处结合缝为闭合状态,结合缝基本没有转角。当弯矩小于273 kN·m时,结合缝处所受弯矩与转角基本呈线性,由于上一个试验阶段出现脱开,无法发挥作用,但相对转角刚度仍然较大,为158 380 kN·m/rad。当弯矩超过273 kN·m后,结构刚度明显降低,挠度随着荷载增大而线性增加,当弯矩增至595 kN·m,结构转角增至0.007 4 rad。此时结合缝转角刚度约为44 680 kN·m/rad,结合缝脱开高度较大。继续加载,试验出现1根预应力筋断裂失效,且后侧工作管与标准管之间结合缝混凝土与钢管节靠右侧的黏结完全脱开,结合缝转角刚度显著降低至5 957 kN·m/rad,转角迅速增大至0.013 9 rad。随着荷载继续增加,余下预应力筋继续发挥作用,荷载增至714 kN·m时,转角增至0.016 5 rad,抗弯刚度增至33 356 kN·m/rad。
在负弯矩工况5加载阶段,当荷载低于405 kN·m时,结合缝张开随着荷载增加而线性增加,转角刚度约为 32 669 kN·m/rad。荷载逐步增加,结合缝处迅速脱开,结合缝上部靠近C型锁扣的混凝土被局部压裂(如图12所示),此时结构丧失部分抗力,刚度降低至15 293 kN·m/rad。当弯矩为547 kN·m时,转角为0.022 rad。当弯矩超过547 kN·m后,左上部位结合缝的CT型锁扣接触上,此时结构转角增速显著降低,抗弯刚度显著增大,增至87 144 kN·m/rad。当弯矩达到827 kN·m时,转角为0.025 9 rad。
3.2 结构挠度
3.2.1 正弯矩压弯试验
正弯矩工况2—4加载阶段结构挠度随荷载偏心距的变化关系曲线如图13所示,可见其变化规律与结合缝转角随荷载变化规律一致,这是因为结构挠度基本由结合缝转角及错动导致,而管节自身变形极小,可以忽略。

图13 正弯矩试验结构挠度-荷载偏心距关系曲线Fig. 13 Relation curves between structural deflection and load eccentricity in positive bending moment test
对比不同工况下挠度变化情况,整个挠度发展过程可以分为6个阶段: 1)弹性受力阶段; 2)结合缝混凝土与钢管节脱开阶段; 3)脱开高度增加、混凝土受压区逐步减小、结构进入非线性阶段; 4)混凝土局部破坏阶段; 5)CT型锁扣贴紧受力、结构刚度上升阶段; 6)CT型锁扣被拉开、结构破坏阶段。
3.2.2 负弯矩压弯试验
负弯矩工况3—5加载阶段结构挠度随弯矩的变化关系曲线如图14所示。
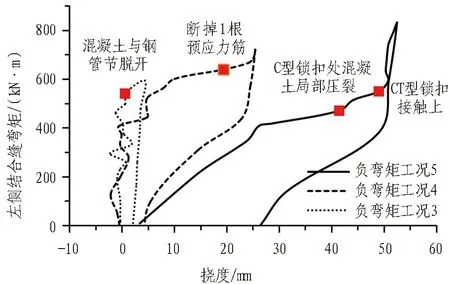
图14 负弯矩试验结构挠度-弯矩关系曲线Fig. 14 Relation curves between structural deflection and bending moment of negative bending moment test
对比负弯矩试验中不同工况下挠度变化情况,整个挠度发展过程同样可以分为6个阶段,且基本与正弯矩试验相同。差异主要体现在阶段3,即与正弯矩试验不同的是,预应力筋位于受拉侧,结构脱开后,预应力筋立即承担大部分拉力,脱开高度增加缓慢。
4 试验结果分析
4.1 结合缝开裂荷载
由于预应力筋外包波纹管,并不与混凝土直接接触,不能像普通钢筋混凝土中的钢筋一样通过黏结发挥作用。在混凝土未开裂之前,预应力筋可以看作荷载形式,使得结合缝内产生一定的弯矩和轴力,用于抵抗千斤顶和结构自重产生的弯矩。
正弯矩试验中,在9根预应力筋试验阶段,当结合缝没有明显张开时,可以认为预应力筋并无明显伸长,此时预应力筋仅作为外荷载考虑。根据锚固端实测数据,此时锚固端实际张拉力为823 kN。采用等效荷载法,预应力在工作管结合缝处产生弯矩为198.64 kN·m,产生轴力为801.91 kN,产生剪力为41.49 kN。临界张开时竖向千斤顶顶力为130 kN,水平千斤顶顶力为1 060 kN。考虑到结构自重会产生弯矩105.436 kN·m,临界阶段工作管结合缝受到549.34 kN·m弯矩、1 862 kN轴力、171.49 kN剪力。
尽管锚固端位置并非在截面高度中心,而是有一定偏心,但锚固位置在受压侧而非受拉侧,因此不考虑局部受压状态。计算结合缝脱开时,结合缝受拉位置的应力状态为:
(2)
(3)
式(2)—(3)中:σ为结合缝外缘拉应力;M为结合缝处弯矩值;I为结合缝截面惯性矩;y为结合缝外缘至中性轴的距离;N为结合缝处轴力值;Ae为结合缝有效截面积;τ为结合缝剪应力;Q为结合缝处剪力值。
代入相应参数计算可得:
σ=1.991 MPa ;
τ=0.145 MPa 。
通过一点应力状态计算,此时结合缝受拉张开部位一点最大应力为:
(4)
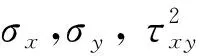
计算结果为
σ1=2.141 MPa 。
另参照型钢与混凝土黏结性能试验研究中推导出的计算公式,型钢板与混凝土之间的黏结强度
(5)
式中:τp为最大黏结强度;c为保护层厚度;h为型钢板厚度;n为箍筋数量;Asv为箍筋截面面积;B为试件宽度;S为箍筋间距;ft为混凝土抗拉强度。
实际结构中,可以将结合缝的混凝土与钢板看作型钢与混凝土的黏结情况,因此取保护层厚度100 m,型钢厚度25 mm,且混凝土内无任何横向箍筋,Asv为0。此次试验混凝土强度等级为C45,根据规范取抗拉强度为2.51 MPa,代入式(5)计算得出:
τp=1.913 MPa 。
根据一点应力状态计算公式,求得一点最大应力为:
σ1=1.913 MPa 。
试验计算结果与理论黏结强度基本一致,相差在12%以内。
而在负弯矩试验中,结合缝受拉张开部位一点最大应力计算结果为σ1′=2.043 MPa,与理论黏结强度相差仅在7%以内。
4.2 结合缝极限荷载
4.2.1 锁扣极限荷载力
结构承载力极限状态表现为工作管结合缝上部CT型锁扣被拉开,结构无法继续承载外荷载出现破坏,锁扣安装和受力简图分别见图15和16。

图15 锁扣安装图Fig. 15 Installation of lock
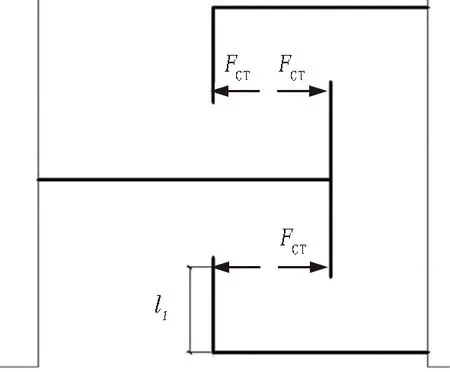
图16 锁扣受力简图Fig. 16 Force on lock
根据试验现象,承载力极限状态下,结构C型锁扣被拉翘,即C型锁扣与钢管节焊缝位置破坏。不考虑CT型锁扣贴紧后相互错动引起的剪力,仅考虑相互之间的压力FCT,临界状态下满足:
(6)
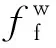
构件制作时采用角焊缝焊接,焊接采用E50型号,焊接强度设计值为200 MPa。角焊缝有效厚度为7 mm,角焊缝计算长度为1 480 mm。作用点距离为17 mm,C型锁扣截面抗弯系数为24 667 mm3。代入相应参数,单个C型锁扣与T型锁扣之间计算临界荷载为:
FCTu=311.75 kN 。
试验过程中,结合缝上部靠近混凝土的C型锁扣的下方表面贴有应变片。结合正弯矩工况4时的锁扣应变试验结果,该应变数值为-167με。假定该C型锁扣端部仅受到来自T型锁扣的挤压力,则该处应变满足:
(7)
式中:σC为C型锁扣应力;FCT1为锁扣压力;E为锁扣弹性模量;ε为C型锁扣应变。
计算所得FCT1=357.2 kN。试验结果高出理论值14%。主要原因是由于靠近混凝土的C型锁扣靠近混凝土一侧受到混凝土约束,部分混凝土承担外荷载,导致实测值大于理论值。
4.2.2 结合缝极限承载力
破坏阶段结合缝受力简图见图17。
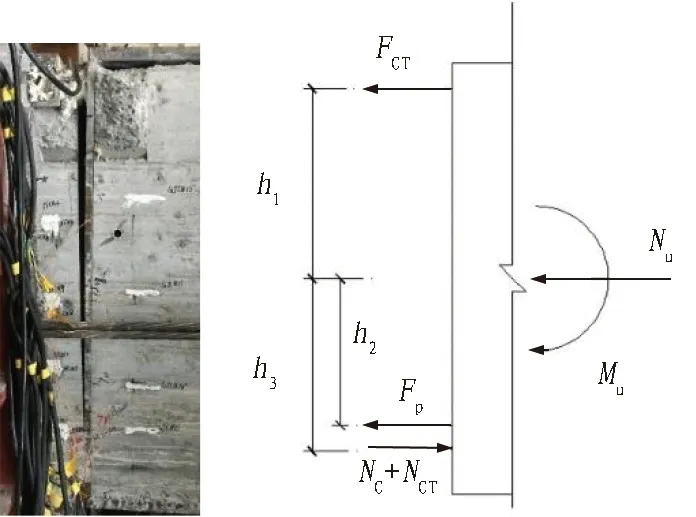
图17 极限状态结合缝受力简图Fig. 17 Stress of joints in ultimate state
FCT+Fp-(NC+NCT)=Nu。
(8)
FCTh1+Fph2-(NC+NCT)h3=Mu。
(9)
式(8)—(9)中:FCT、NCT分别为结合缝上部锁扣拉力与下部锁扣压力;Fp为预应力筋拉力;NC为结合缝下部混凝土所受压力;Nu、Mu分别为极限状态下结构所受轴力与弯矩;h1、h2、h3为各个内力至截面中心的距离。
根据实际安装位置及量测结果,h1=441 mm,h2=340 mm,h3=425 mm。结构破坏时,结构无水平顶力,仅有竖向顶力159.7 kN。试验时有6根预应力筋提前张拉,预应力产生142.52 kN·m弯矩、534.7 kN轴力,即最终破坏时Nu=534.7 kN。
同时,根据锚固端实测结果,最终破坏时,预应力筋上合力约为Fp=1 440 kN。根据上述锁扣承载力计算结果,综合来看,破坏阶段单组CT型锁扣的极限承载力为上下2个C型锁扣的承载力之和,即FCT=FCTu+FCT1=668.75 kN。
代入各项数据,计算出临界抗弯承载力为Mu=474.3 kN·m。实测弯矩承载力为Mureal=513.7 kN·m,超过理论计算值约8%,在试验误差范围内。实测值高于理论值的原因主要与预应力筋受力有关,预应力合力的测试装置采集频率较低,而破坏阶段维持时间很短,因此引起相应测试值的大幅波动,数据处理时考虑平均值,导致测试出来的预应力筋合力低于真实合力,进而理论计算抗弯承载力偏低。
5 结论与讨论
1)根据试验结果,结合缝脱开、混凝土局部破坏、CT型锁扣紧贴以及CT型锁扣脱开是结构的重要性能点。以正弯矩试验结果为例,结合缝混凝土与钢管节脱开后,结合缝转角刚度下降了83%。而后结合缝底部混凝土出现局部裂开,预应力筋承受所有拉力,结构刚度又出现降低,转角刚度下降65%,仅为初始刚度的6%。随着CT型锁扣贴紧受力,结构刚度又出现陡增,转角刚度增加了3.87倍。但随着荷载继续增加,CT型锁扣一旦出现脱开,转角刚度降至2.5%,结构出现破坏。
2)根据正、负弯矩试验中不同工况条件下的试验结果及现象对比,试件挠度、结合缝张开均可以划分为6个发展阶段: ①弹性受力阶段,结构挠度略微增加,无明显结合缝张开与错台; ②结构内部出现混凝土与钢管节脱开,预应力筋受力增加; ③随着荷载增大,脱开高度增加,混凝土受压区逐步减小,结构进入非线性阶段,结构挠度、结合缝张开与错台都有明显增加; ④结合缝混凝土局部破坏,结构各项刚度进一步降低; ⑤CT型锁扣贴紧受力,承担部分外荷载,结构各项刚度显著提升; ⑥CT型锁扣被拉开,无法继续承受外荷载,结构破坏,达到承载力极限状态。
3)正、负弯矩试验中,结合缝混凝土截面最大拉应力分别为2.141 MPa、2.043 MPa,超过混凝土与钢管节之间的黏结应力,黏结脱开。临界黏结应力与根据文献计算结果1.913 MPa相差7%~12%。
4)正弯矩试验中,结构最终达到承载力极限状态。在结构承载力极限状态下,结合缝上部锁扣、下部预应力筋承受拉力,底部混凝土与底部锁扣承受压力,破坏形式表现为上部CT型锁扣脱开,无法继续承担外荷载,最终结构破坏。实测弯矩承载力为Mureal=513.7 kN·m,与理论计算值Mu=474.3 kN·m误差约8%,在试验误差范围内。
本文通过开展束合管幕结构结合缝的足尺压弯试验,初步研究了该新型结构的受力性能与破坏机制,后续将开展无黏结预应力筋、结合缝构造设计对结构受力性能的影响研究,进一步提出该结构的设计方法,为实际工程提供指导,也为束合管幕结构在大跨暗挖车站中应用奠定基础。

