土压平衡盾构长距离施工运输模型应用研究
——以北京地铁新机场线一期工程为例
杨志勇, 白志强, 李元凯, 高洪吉, 江玉生, 孙 伟, 孙正阳, 5
(1. 中国矿业大学(北京)力学与建筑工程学院, 北京 100083; 2. 北京市轨道交通建设管理有限公司,北京 100068; 3. 城市轨道交通全自动运行系统与安全监控北京市重点实验室, 北京 100068; 4. 中铁十四局集团有限公司, 山东 济南 250014; 5. 北京城建集团有限责任公司博士后科研工作站, 北京 100088)
0 引言
随着我国城市规模不断扩大,出现了城市快速轨道交通,这些快速轨道交通线路列车停靠车站更少,区间隧道更长,车辆行驶速度更快,催生出长距离城市盾构隧道,这对盾构施工组织提出了更高要求。土压平衡盾构掘进过程中,物料及渣土运输、掘进、管片拼装三者之间相互衔接。对于长距离盾构隧道而言,随着运输距离增加,洞内水平物料、渣土运输将成为影响盾构施工效率的关键因素[1-3]。
目前,土压平衡盾构施工常见物料及渣土运输方式为有轨运输,这种方式单次运载量大,但随着运输距离加长,运输效率显著降低。有鉴于此,个别长、大盾构隧道为了加快盾构施工速度,采用了连续皮带输送机+垂直皮带输送机组合为皮带输送机出渣系统运输渣土,实现物料运输和渣土运输的分离,加快施工效率。
近年来,许多学者结合实际工程对盾构/TBM出渣方式的优选进行了研究。齐梦学[4]从技术、经济和工期方面分析龙门吊与垂直皮带机出渣的差异,得出在城市地铁双护盾及开敞式TBM施工中,垂直皮带机出渣技术具有运输效率高、不占用TBM掘进时间、故障率和综合成本低等优势; 王智远等[5]通过经济性、环保性、物料运输效率等方面综合对比,选择连续皮带输送机系统作为TBM施工最优出渣系统; 陈鹏等[6]对独头掘进5 468 m的长距离泥水盾构隧道进行物料运输优化,并建立长距离隧道车辆无轨运输优化模型,结果表明该优化模型可为苏通GIL综合管廊工程洞内物料运输方案提供可靠的理论指导; 徐华升等[7]通过建立物料运输规划数学模型并进行求解,找到了总体费用最低的物料调运方案; 封坤等[8]通过建立模糊综合评判模型,对盾构隧道内无轨运输系统进行优化; 张宁川[9]在兼顾配置成本合理性和设备运行可靠性的基础上,对土压平衡盾构的轨道运输系统配置方案进行优选; 齐春杰[10]为了解决大直径土压平衡盾构在复杂多变地层中高效出渣的难题,通过对现场出渣情况记录、分析及调整,得到了连续皮带输送机可高效进行渣土运输的结论; 梁峻海等[11]为研究盾构隧道洞内无轨运输具体的车辆调度方案,依托苏通GIL综合管廊工程,提出单车道车辆调度方案,建立运输车辆调度数学模型,通过模型分析得出单环运输周期和单车道长度呈线性关系,并得出该工程最小掘进周期与单车道极限长度。
通过对国内文献进行研究分析,发现关于土压平衡盾构隧道内部物料及渣土运输方面的研究大多限于工程经验总结与相关运输方式的定性对比,少量文献对盾构出渣系统的选取进行定量计算,但对于有轨运输与组合运输2种运输方式的施工效率尚缺乏统一的理论与标准。本文基于土压平衡盾构施工循环流程,建立物料及渣土运输模型,对上述2种运输系统的施工效率进行理论分析和计算,并结合北京地铁新机场线一期盾构隧道工程实例对理论计算结果进行验证,以期为类似长距离隧道工程物料及渣土运输方式的选取及设计提供一定的理论依据与工程参考。
1 工程概况
北京地铁新机场线一期工程北起草桥,与19号线相接,南至新机场北航站楼,线路途经大兴、丰台2个行政区,全长约46 km,是市区直达新机场的轨道交通专线。地下段中盾构区间隧道长度为14.8 km,共分为4个标段、5个区间,下穿地层主要为砂卵石地层,平均线路埋深12~26 m。盾构区间隧道距离较长,其中2号风井—3号风井区间右线全长3 847 m,为全线最长盾构区间。盾构隧道开挖直径9 114~9 150 mm,管片外径8 800 mm、环宽1 600 mm、厚度450 mm。
新机场线一期工程盾构区间施工工期十分紧张,仅18个月(含盾构设备采购选型)。两相邻隧道1号风井—2号风井、2号风井—3号风井盾构区间分别采用有轨运输系统与有轨运输+皮带输送机(包括水平连续皮带输送机+垂直皮带输送机)组合系统(简称组合运输系统)2种盾构施工物料及渣土运输方式。盾构区间概况见表1。

表1 盾构区间概况Table 1 Overview of shield sections
2 运输系统模型建立
2.1 运输方式
根据工程特点和工程实际投入,将盾构掘进分为3个区域: Ⅰ 区为垂直运输区域,Ⅱ 区为水平运输区域,Ⅲ 区为盾构设备区。盾构施工掘进分区如图1所示。

图1 盾构施工掘进分区示意图Fig. 1 Sketch of shield tunneling zoning
设定同一列车编组在盾构后配套处开始卸载管片等物料,至其再次返回盾构后配套处的时间间隔为1个运输循环周期。
2.1.1 有轨运输系统
轨道列车同时携带管片车、浆液车与渣土车,自洞口吊装完成后驶入隧道,在盾构掘进过程中需将渣土车移动至后配套皮带输送机卸料端下方装载渣土,同时卸载管片、浆液等物料,待盾构完成1环掘进后驶出隧道至始发井垂直运输。盾构施工循环分步工序如图2所示。

图2 盾构施工循环分步工序示意图Fig. 2 Sketch of processes of shield tunneling cycle
通过现场采样,统计有轨运输系统盾构掘进循环主要工序时间参数,结果见表2。

表2 有轨运输系统盾构掘进循环主要工序时间参数统计Table 2 Time parameters statistics of main working procedure of shield tunneling cycle in rail transport system
2.1.2 组合运输系统
相比传统有轨运输系统,组合运输系统在盾构掘进过程中,螺旋输送机将渣土直接运输到后方连续皮带输送机上,随着皮带输送机运输出隧道直至进入地面渣土池; 轨道列车携带管片等物料自盾构始发井吊装完成后运输至盾构后配套处卸载,之后列车即可驶出隧道至盾构始发井继续进行吊装加载。
组合运输系统可实现盾构渣土连续运输,渣土直接转运至地面渣土池,垂直运输时间缩短,轨道列车空载驶出隧道,其余施工工序与有轨运输系统相同。组合运输系统盾构掘进循环主要工序时间参数统计见表3。

表3 组合运输系统盾构掘进循环主要工序时间参数统计Table 3 Time parameter statistics of main process of shield tunneling cycle in combined transport system
2.2 列车编组
根据工程特点与实际投入,盾构施工期间隧道内同步铺设单线轨道。随着隧道掘进距离增加,运输效率显著降低,增加固定式道岔与移动会车平台,分3个阶段提升多列编组运行要求。
1)阶段1。始发掘进期间,由于盾构整体长度影响,列车编组为1台电瓶机车+4台渣土车(组合运输系统无渣土车,阶段2、3相同)+2台砂浆罐车+3台管片车,在盾构始发井主体结构及隧道内部铺设单线轨道。
2)阶段2。隧道掘进距离较长阶段,在始发洞门处铺设固定道岔及4轨双线轨道。投入2组列车编组(1台电瓶机车+4台渣土车+2台砂浆罐车+3台管片车)。
3)阶段3。运输效率显著降低阶段,在隧道内部增加移动会车平台,随盾构向前掘进而移动,洞内列车编组数量增加至3组。
2.3 道岔布设
盾构隧道水平运输最优原则为: 物料与管片提前到达盾构后配套处,利用盾构流程转换的合适时间卸载物料及管片,尽量缩短盾构空置时间。
为了实现最优运输组织,结合表2、3可知,在有轨运输条件下,单组列车完成1次运输循环所需时间须小于管片拼装时间,如式(1)所示; 组合运输系统完成1次运输循环所需时间须小于盾构掘进与管片拼装时间之和,如式(2)所示。否则,将出现盾构停机等待时间,降低盾构施工效率。
(1)
(2)
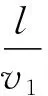
轨道列车在一个运输循环周期里的最大水平运输距离称为车辆极限运输距离lmax,即始发洞门至盾构后配套处距离。在超过车辆极限运输距离lmax之后需布设道岔,同时增加轨道列车编组数量,以满足管片物料运输需求。2种盾构运输系统轨道列车单环单组运输循环周期如图3所示。
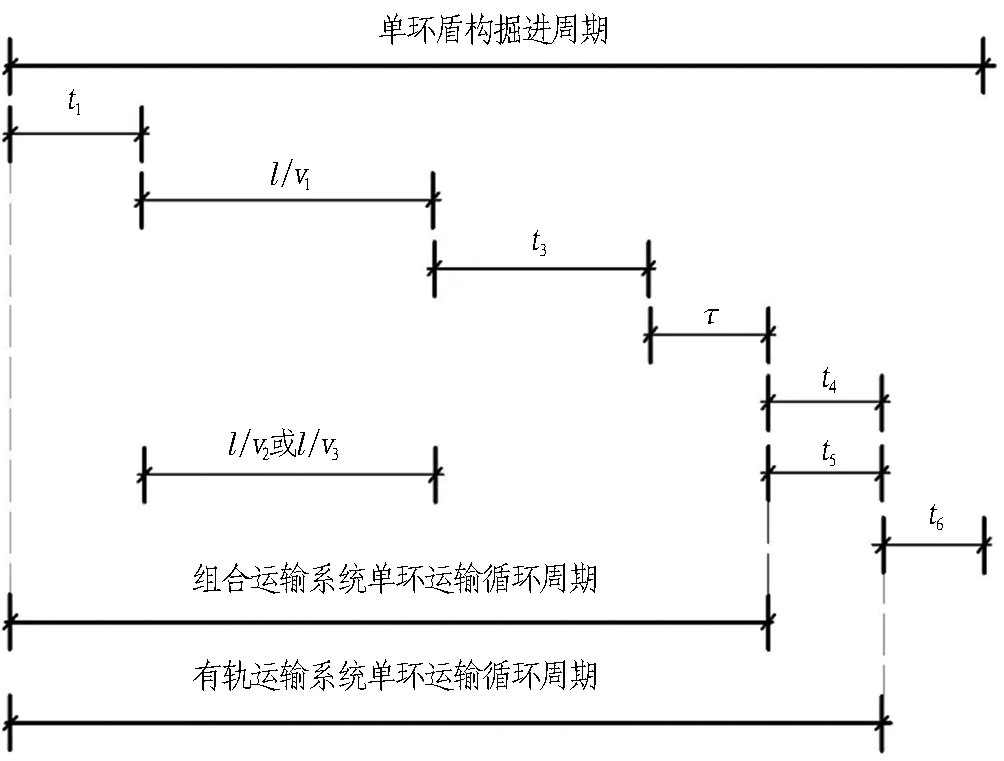
图3 2种运输系统单环单组运输循环周期示意图Fig. 3 Sketch of single-loop and single-group transportation cycle of two transport systems
由图3分析可知,有轨运输系统与组合运输系统单环单组完成1次运输循环周期所需时间为:
(3)
(4)
式(3)—(4)中:T为有轨运输系统单环单组运输循环周期;T′为组合运输系统单环单组运输循环周期;τ为车辆滞留时间。
由式(3)—(4)化简得到2种运输系统轨道列车在隧道内部运输距离l的计算表达式分别为:
(5)
(6)
当滞留时间τ=0时,2种运输系统车辆极限运输距离lmax的计算表达式分别为:
(7)
(8)
结合式(7)—(8),2种运输系统单程极限运输距离计算结果见表4。

表4 2种运输系统单程极限运输距离Table 4 One-way limit transport length of two transport systems
由隧道极限运输距离反推得出道岔最晚布设时机。在有轨运输系统条件下,盾构始发掘进时即需安装固定道岔; 在组合运输系统条件下,水平隧道距离达1 700 m时布设固定道岔即可满足盾构隧道水平运输需求。
2.4 2种运输系统模型建立
2.4.1 有轨运输系统模型建立
有轨运输系统盾构始发掘进后随即布设道岔,同时投入2组轨道列车编组,2组列车可交替进行垂直运输。
结合上述分析,在一定运输距离lX范围内,盾构掘进时间/渣土加载时间与管片拼装时间之和是制约完成盾构掘进循环的主要因素,如式(9)所示:
(9)
当且仅当滞留时间τ=0时,可求得最大运输距离
lX≤1 214 m。
(10)
当运输距离大于1 214 m,垂直运输时间与水平运输时间之和转变为制约盾构掘进循环的主要因素,此时完成1次掘进循环所需时间
(11)
结合式(9)—(11),通过对不同隧道距离进行分析,得出有轨运输系统条件下盾构完成1次掘进循环时间计算模型。当且仅当滞留时间τ=0时,计算模型表达式为:
(12)
2.4.2 组合运输系统模型建立
结合表4中组合运输系统单程极限运输距离,在运输距离l≤1 700 m阶段,盾构掘进时间与管片拼装时间之和是制约盾构完成掘进循环的主要因素; 当运输距离l>1 700 m时,垂直运输时间与水平运输时间之和转变为制约盾构掘进循环进度的主要因素。
综上所述,当且仅当滞留时间τ=0时,在组合运输系统条件下完成1次盾构掘进循环时间计算模型如式(13)所示:
(13)
3 工程分析
基于上述研究,分别对2种运输系统条件下盾构掘进循环时间进行理论预测,结合现场实测掘进循环时间数据,进行模型对比验证。
3.1 有轨运输系统数据对比分析
基于式(12)理论计算结果与现场实测数据,对北京地铁新机场线一期工程1号风井—2号风井区间的预测掘进循环时间与实测掘进循环时间进行对比分析,同时计算实测时间相比理论预测时间的增量百分比,计算结果如图4所示。
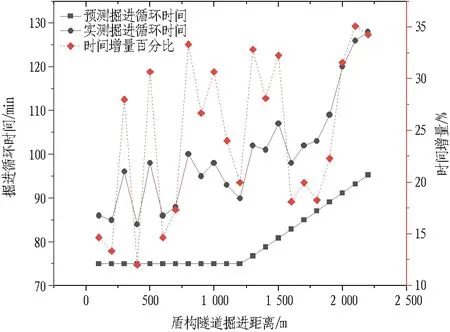
图4 有轨运输系统预测时间与实测时间对比分析Fig. 4 Comparative analysis of predicted time and actual measured time of transport system
通过图4对比分析可知,预测掘进循环时间与实测掘进循环时间曲线走势基本相同,但实测掘进循环时间始终大于预测掘进循环时间。运输距离为400 m时,预测时间与实测时间相差最小,实测时间相比预测时间增加12%; 运输距离为2 100 m时相差最大,最大增加34%。随着运输距离增加,盾构掘进循环实测施工时间与理论预测时间差值逐渐增大,运输效率降低越加明显。
综合分析上述现象,原因为: 有轨运输系统施工连续性较差,且理论预测计算主要考虑盾构施工循环关键因素,对现场施工调度、组织安排以及龙门吊设备故障检修时间等次要因素未考虑在内,导致实测掘进循环时间始终大于预测掘进循环时间。
3.2 组合运输系统数据对比分析
同理,基于式(13)对北京地铁新机场线一期工程2号风井—3号风井区间预测掘进循环时间与实测掘进循环时间进行对比分析,同时计算实测时间相比理论预测时间的增量百分比,计算结果如图5所示。
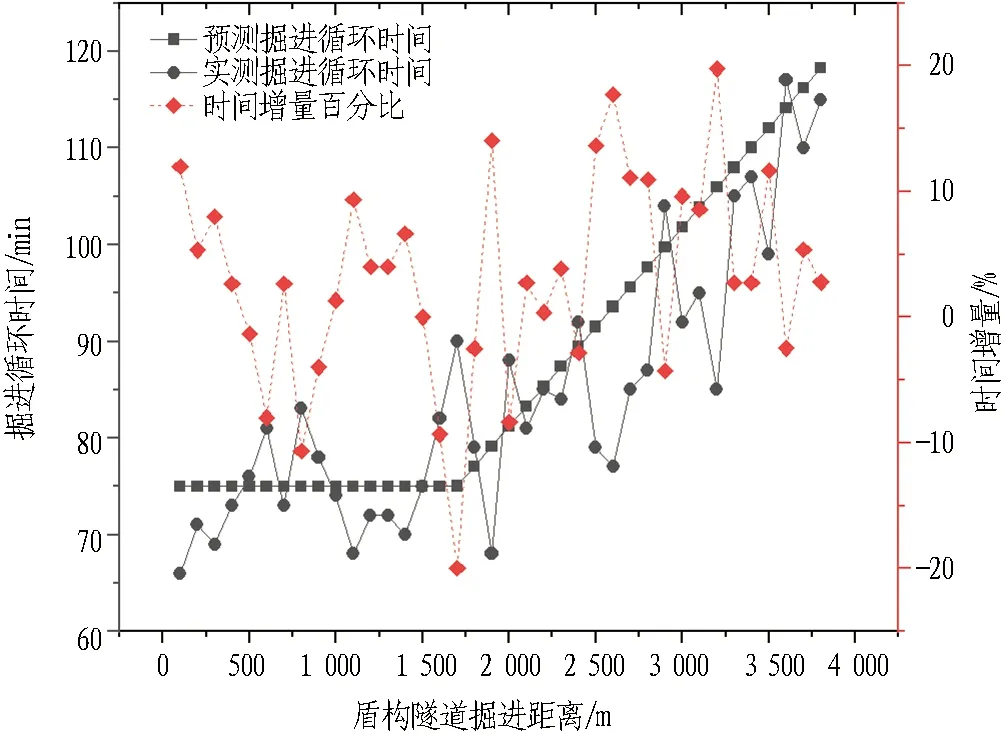
图5 组合运输系统预测时间与实测时间对比分析Fig. 5 Comparative analysis between predicted time and tactual measured time of combined transport system
通过图5对比分析可知,实测掘进循环时间始终围绕理论预测掘进循环时间上下波动,并多次出现曲线相交情况,即实际施工达到理论预期。运输距离为1 700 m时,预测时间与实测时间相差最大,最大增加19%。总体而言,组合运输系统盾构掘进循环理论预测时间与实测施工时间相差较小,在现场实际施工过程中,更容易达到理想施工效果。
相比有轨运输系统,组合运输系统受到次要因素影响较小,且由于物料运输与渣土运输分离,进一步加快了施工效率,因此出现多次实际施工情况达到理论预期效果。
3.3 2种运输系统适用施工距离分析
2种运输系统实测施工时间差值与有轨运输系统实测施工时间进行比值计算,定义该比值为2种盾构运输系统的施工工效,如式(14)所示。

(14)
基于3.1节、3.2节对2种运输系统实测掘进循环时间数据进行对比,将对比分析结果与工效比值进行绘图分析,结果如图6所示。

图6 2种运输系统实测掘进循环时间和施工工效对比Fig. 6 Comparison of measured driving cycle time and construction efficiency between two transport systems
由图6分析可知,运输距离在600 m附近时,2种运输系统完成1次掘进循环相差时间最小,组合运输系统相比有轨运输系统施工工效增加5.8%; 在1 700 m附近,2种运输系统施工工效再次相差较小,为11.8%,随后施工工效差值逐步增大,在2 200 m附近达到峰值,最大增加39%。
综上所述,2种运输系统实测施工工效拐点在600 m与1 700 m附近,即当运输距离小于600 m时,2种运输系统施工工效相差最小,且皮带输送机出渣系统初期投资成本较大,综合成本、造价等因素宜优先选用有轨运输系统; 当运输距离在600~1 700 m时,2种盾构运输系统施工工效基本相同; 运输距离大于1 700 m时,出于施工工效考虑,宜选取组合运输系统。
4 结论与讨论
本文依托北京新机场线一期工程1号风井—2号风井、2号风井—3号风井盾构区间,基于盾构掘进循环模型对有轨运输和组合运输2种运输系统建立模型并求解预测。结合现场实测掘进循环时间分析,得到结论如下:
1)在有轨运输系统条件下,盾构预测掘进循环时间与实测掘进循环时间最小相差12%,最大相差34%,随着运输距离增加,时间差值逐渐增大,工效降低越加明显,越难达到理论施工期望。
2)在组合运输系统条件下,实测掘进循环时间始终围绕理论预测掘进循环时间上下波动,并多次出现曲线相交情况,即实际施工达到理论预期,运输距离为1 700 m时,时间差值最大仅为19%。总体而言,理论预测时间与实测施工时间相差较小,在现场实际施工过程中,更容易达到理想施工效果。
3)组合运输系统相较有轨运输系统施工工效最小增加5.8%,最大增加39%; 结合施工工效拐点分析,得出当盾构隧道运输距离小于600 m时,优先选用有轨运输系统; 运输距离在600~1 700 m时,2种运输系统均可选择; 运输距离大于1 700 m时,出于施工工效考虑,宜选取组合运输系统。
本文旨在研究2种运输系统施工效率问题,且重点在于水平运输出渣方式优选,因此,对于垂直运输距离等参量未做深入考虑,仅结合现场实测样本数据对2种运输系统中垂直运输部分进行定量赋值,简化模型建立条件。同时,文章未针对成本、环保、造价等其他因素对于施工的影响进行深入分析,后续仍需进一步研究。

