S型空间曲线圆形顶管管道应力分析
——以宁波市电力隧道顶管工程为例
许有俊, 韩志强, *, 张 朝, 孟毅欣, 高胜雷
(1. 内蒙古科技大学土木工程学院, 内蒙古 包头 014010; 2. 内蒙古科技大学 矿山安全与地下工程院士专家工作站, 内蒙古 包头 014010; 3. 内蒙古科技大学 内蒙古自治区高校“城市地下工程技术研究中心”,内蒙古 包头 014010; 4. 北京市政建设集团有限责任公司, 北京 100079)
0 引言
近年来,大直径、长距离圆形顶管非开挖技术大量应用于市政管道工程中。受周围环境的影响,一些顶管工程为了避让既有的地下结构物而不得不采用复杂的S型空间曲线轴线,即平面线形为S型、纵断面线形为曲线型。与直线型、一般曲线型顶管工程相比,由平曲线与竖曲线叠合形成的S型空间曲线在顶管施工过程中,管土相互作用、土体扰动、顶管姿态控制等方面更为复杂[1-2]。
目前,国内外专家、学者采用理论计算、试验、数值模拟等方法对顶管顶进施工过程中的力学问题进行了研究,并取得了丰富的研究成果。理论计算方面,朱合华等[3]推求了曲线顶管施工过程中管体法向和纵向变形的理论表达式;王承德[4]、熊翦[5]、曾勤[6]对顶管施工中的顶力计算进行了公式修正;Sofianos等[7]对比分析了挖掘面稳定假设的弹性解和太沙基理论管土全接触的解。试验研究方面,Shou等[8]通过室内试验估算理论顶推力,并与施工现场顶推力进行比较,研究管土间相互作用的分布规律;魏纲等[9]通过现场实测数据对顶进过程中管道纵向、环向钢筋应力以及管土接触应力进行分析,得到管道的应力变化规律;刘翔等[10]、张鹏等[11]通过现场试验对钢筋混凝土顶管的管壁接触压力,环向钢筋应力、应变和轴力进行了测试;张耀等[12]通过现场试验得到在施工荷载、水土压力等三维荷载作用下顶管各部位的应变和管土接触应力时程响应;牛国伦等[13]考虑基于注浆压力的情况下顶管施工过程中管节荷载的分布与变化规律。数值模拟方面,林荣安等[14]将ABAQUS数值模型管片土压力、轴力及纵向应力的变化规律分别与实测结果进行对比,研究荷载条件下管片轴力和弯矩的变化情况;Barla等[15]采用数值分析软件模拟了非饱和土中顶管施工过程的力学特性;黄吉龙等[16]采用数值法分析顶管和周围土层的应力与变形,研究了施工过程中顶管和地基土体的力学效应。
综上所述,国内外专家、学者针对直线形、一般曲线形顶管施工力学特征开展了大量的研究。圆形顶管在一般曲线段顶进时,管节环向钢筋应力分布均匀,应力变化范围和变化规律基本相似,数据波动不大;管节纵向应力分布方面,管顶和管底表现为内拉外压,管腰表现为内压外拉,管壁外侧应力大于内侧应力,且基本保持对称;管土接触应力大小分布为管底>管顶>管腰。但对长距离、大直径、空间S型曲线顶管顶进过程中的管道受力变化规律、管土相互作用等问题尚不清楚。为此,本文依托宁波市电力隧道顶管工程,对曲线顶管施工引起的管道环向、纵向钢筋应力以及管土接触应力共同受力变形和顶管施工参数引起的管道应力变化进行深入分析,并结合数值模拟进行验证和拓展。以期本文研究结果为S型空间曲线顶管隧道施工和管道设计提供借鉴。
1 现场试验概况
1.1 工程概况
宁波市鄞州区电力隧道2#井到1#井共长863.685 m,取隧道前190 m的S型空间曲线段为研究对象。试验区段由2段复合曲线组成,右转向曲线段S1由平曲线半径R=500 m,竖曲线半径R=3 000 m,坡度i=0.99%的直坡段构成;左转向曲线段S2由平曲线半径R=600 m,坡度i=0.99%的直坡段构成。管道所在土层为③淤泥质黏土层。该隧道采用泥水平衡顶管施工,管道为内径3.50 m、外径4.14 m、壁厚0.32 m的钢筋混凝土管。顶管施工平面图见图1,地质剖面见图2。

图1 顶管施工平面图(单位: m)Fig. 1 Plan of pipe jacking (unit: m)
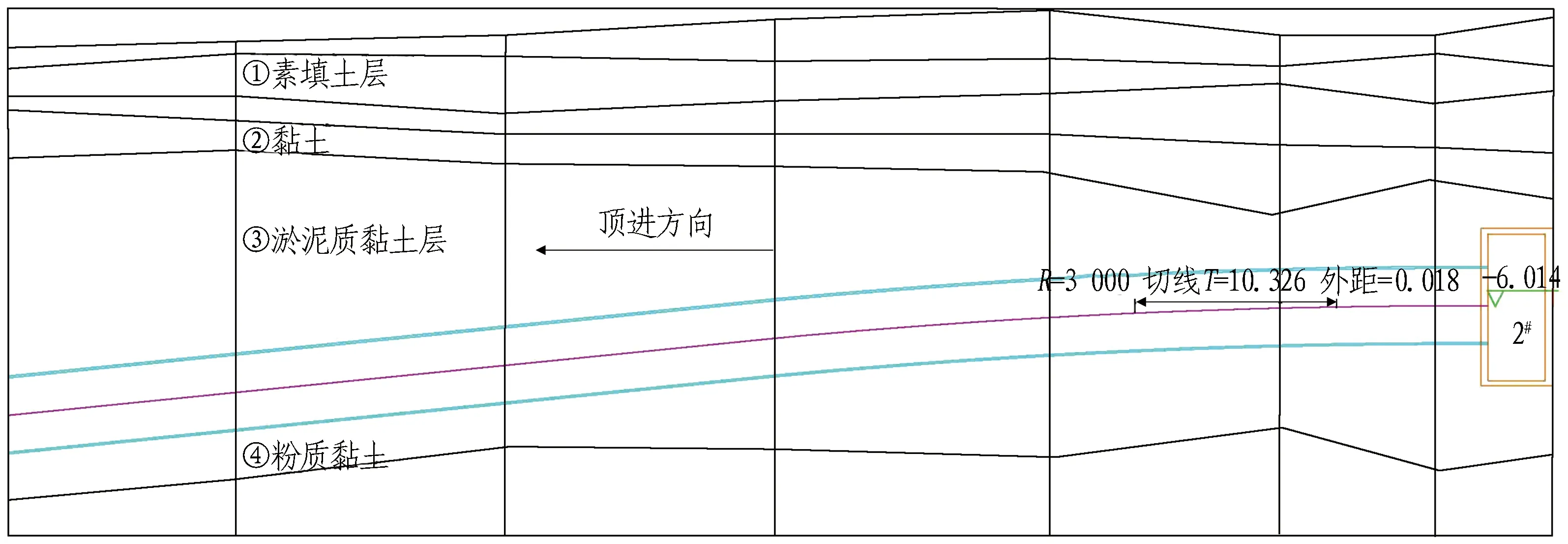
图2 地质剖面图(单位: m)Fig. 2 Geological profile (unit: m)
1.2 测试方案
为了研究S型空间曲线施工顶进过程中的管道受力情况和施工参数如何影响管道受力问题,在试验管道四周,内、外2层钢筋笼以及管道前、后端都布置JTM-V1000型振弦式传感器,以研究管道受力情况;在管壁中间处布设JTM-V2000A(C)型振弦式土压力计,以研究管土相互作用。具体布置方式为: 在距管口两端30 cm处布置环向和纵向钢筋应力计,前端编号为H1—H8(H2已损坏)和Z1—Z8,后端对应位置编号为H9—H16和Z9—Z16,共32个;管壁中间布设4个土压力盒,编号为TY1—TY4。随管道施工顶进采集钢筋频率,并将其换算为应力进行分析。试验管道尺寸及传感器布置如图3和图4所示。
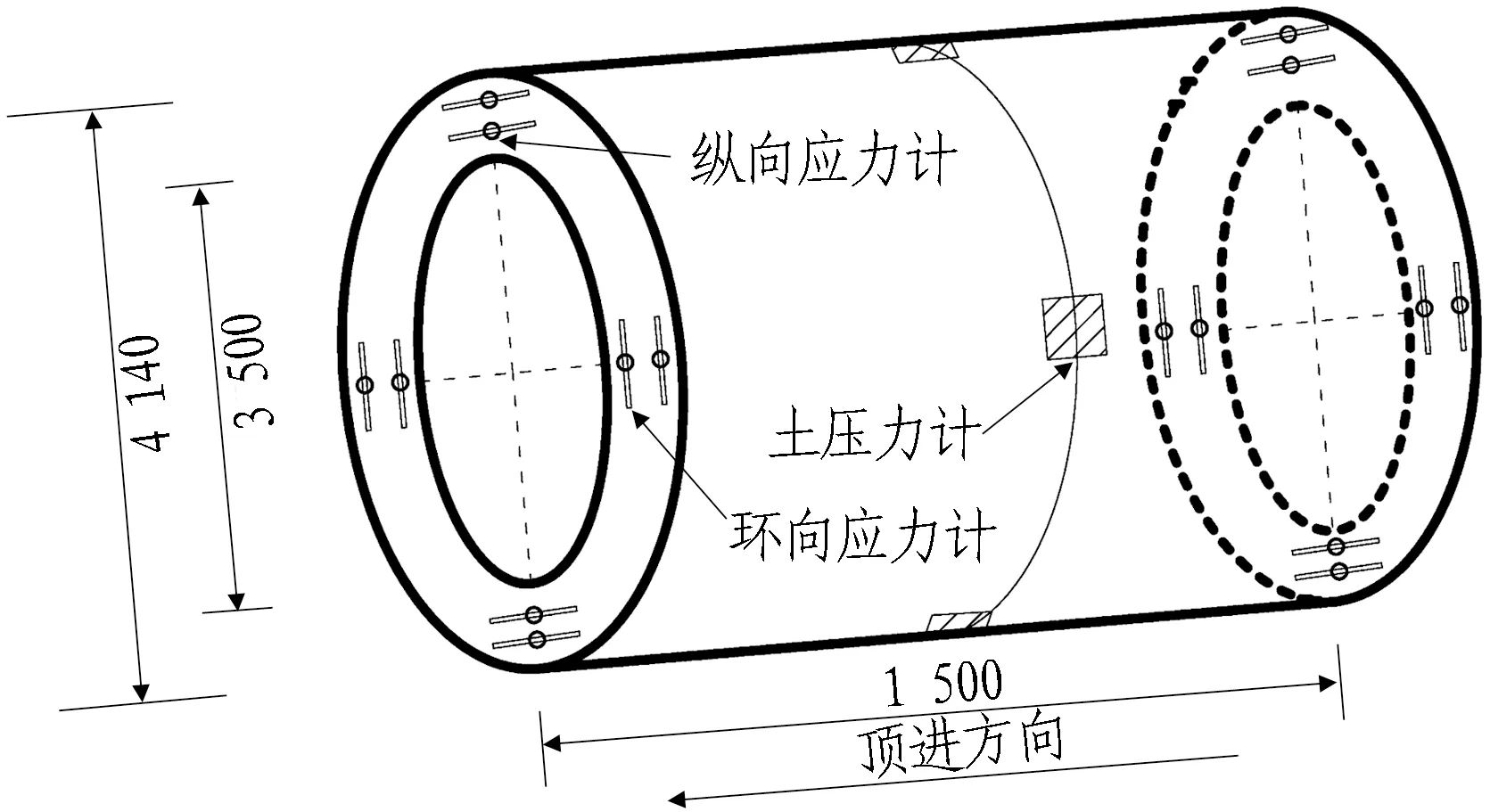
图3 试验管道尺寸(单位: mm)Fig. 3 Dimension diagram of test pipe(unit: mm)
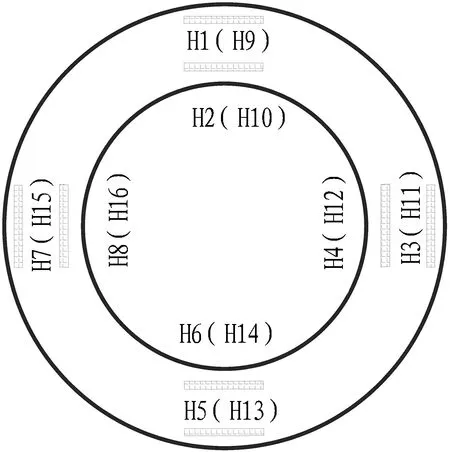
(a) 环向应力计
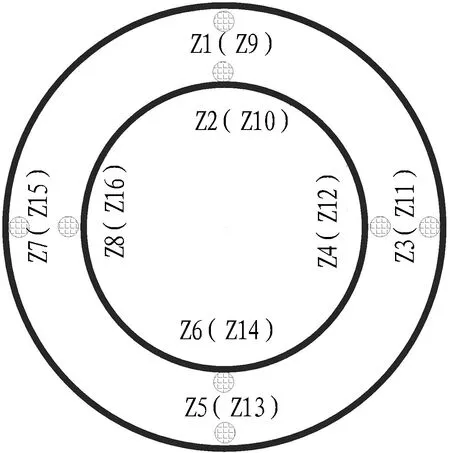
(b) 纵向应力计
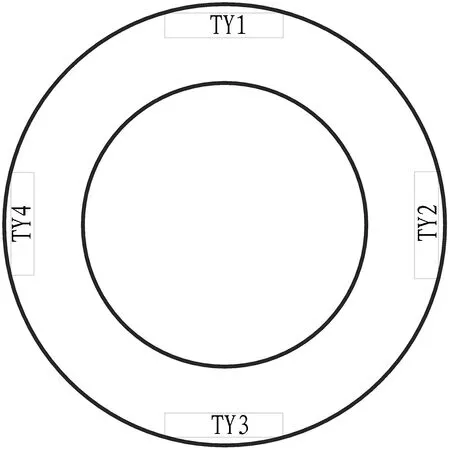
(c) 土压力计图4 传感器布置图Fig. 4 Sensor layout
2 现场实测数据分析
2.1 管道钢筋应力
当试验管道进入曲线段便开始实时记录监测数据,并把实测数据本身的变化规律与当时的施工状况、顶进状态、人为因素等结合进行分析研究,得出在S型空间曲线段顶进过程中管道环向和纵向钢筋受力形态,管道与土体接触状态及施工方式对管道变形规律的影响,可为管道的结构设计以及顶管施工提供参考依据。由于采集数据时管道处于加载或卸载状况,且数据对应的顶进距离间隔不同,因此数据波动较大。
2.1.1 环向钢筋应力实测分析
管道环向钢筋应力主要受注浆压力和施工方式的影响,其受力状态可在一定程度上反映管道横向的受力和形变情况。
管顶和管底环向钢筋应力随顶进距离的变化曲线分别如图5和图6所示。由图可知,在竖直方向上,管顶钢筋应力主要在-8~6 MPa波动,管底钢筋应力主要在-15~10 MPa波动。在整个S型曲线段管顶和管底外侧主要受拉应力,内侧主要受压应力。进入曲线段S1后开始注入触变泥浆,在60 m处注浆量增加至1.5 m3,触变泥浆失水后在管周形成一层泥皮稳固土体,此处环向钢筋应力明显减小。但随着管道向斜下方施工顶进,覆土厚度增加,环向钢筋所受到的土压力、孔隙水压力、注浆压力有所不同而导致应力出现波动。

图5 管顶环向钢筋应力随顶进距离的变化曲线Fig. 5 Variation of circumferential stress at pipe top with jacking distance
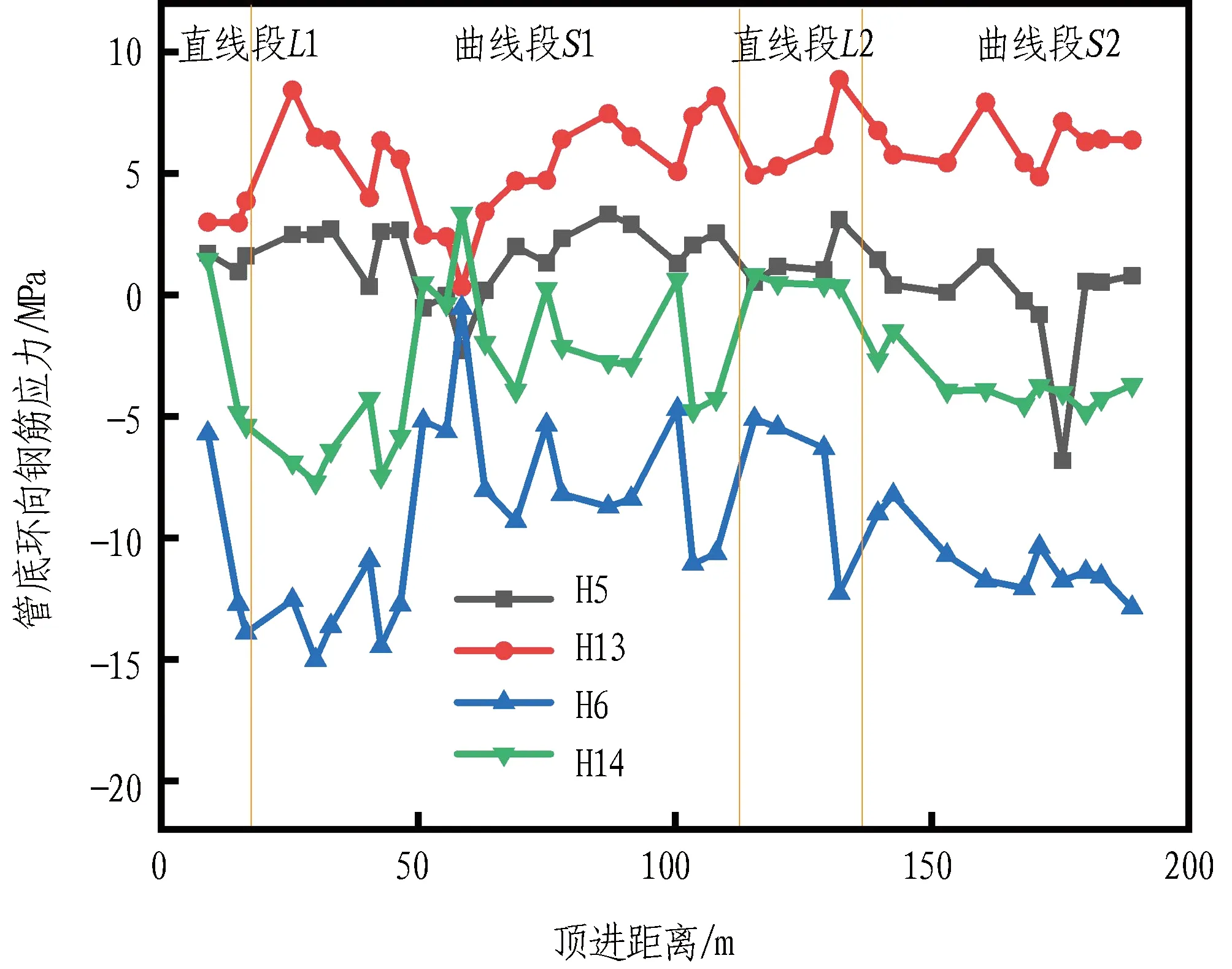
图6 管底环向钢筋应力随顶进距离的变化曲线Fig. 6 Variation of circumferential stress at pipe bottom with jacking distance
管腰左侧、右侧环向钢筋应力随顶进距离的变化曲线分别如图7和图8所示。由图可知,在水平方向上,管腰左侧钢筋应力主要在-15~17 MPa波动,管腰右侧钢筋应力主要在-12~16 MPa波动。S1曲线段的触变泥浆注入量为1.5 m3,进入S2曲线段后触变泥浆注入量为3 m3,增加注浆量可减少地层扰动对环向钢筋应力的影响,因此S2曲线段数据更为平稳,同时纠偏使得管腰左侧处管土间隙大,所以此处注浆压力偏大,导致管腰左侧环向钢筋应力大于右侧。在S型曲线段上,管腰环向钢筋应力并未因转向而发生明显变化,整个受力状态为外侧受压,内侧受拉。管道内外层钢筋存在一定的间隙,受力略有不同,管腰内侧钢筋应力略大于外侧。
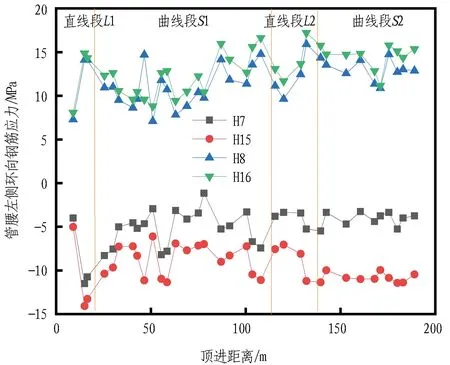
图7 管腰左侧环向钢筋应力随顶进距离的变化曲线Fig. 7 Variation of left circumferential stress at left pipe waist with jacking distance

图8 管右环向应力随顶进距离的变化曲线Fig. 8 Variation of circumferential stress at right pipe waist with jacking distance
据分析可知,圆形顶管在S型曲线段顶进时,环向钢筋应力受转弯影响不显著,竖直和水平纠偏产生不均衡的管间间隙和土体抗力,导致管周注浆压力不同,使管道受到不均匀、非对称的力,数据波动偏大,且规律性不强,因此环向钢筋应力主要受管周土压力和注浆压力的影响。由于泊松比效应限制了管道钢筋的自由膨胀或收缩变形,管口设有2层木衬垫后,管道视为柔性管,在不均匀、非对称受力状态下,管道大致呈现出“横鸭蛋”的椭圆状形变,如图9所示。
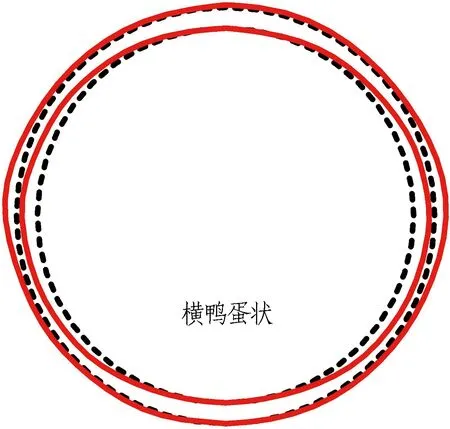
图9 管道横截面形变图Fig. 9 Cross-section deformation of pipeline
2.1.2 纵向钢筋应力实测分析
纵向和环向钢筋频率同时采集,两者处于同一施工状态下。纵向钢筋应力受顶力和顶进轨迹影响,其值反映了管道在复杂受力状态下的应力变化情况,也体现了管道的形变状况。
管顶和管底纵向应力随顶进距离的变化曲线分别如图10和图11所示。由图可知,在竖直方向上,管顶钢筋应力主要在-8~9 MPa波动,管底钢筋应力主要在-2~11 MPa波动。直线段L1开始加载后,出现67 mm的“磕头”现象和向上纠偏。大程度纠偏使应力急剧变化,此时顶管受压,管底受拉。进入S1曲线段后顶管机轨迹出现2次较大程度的轴线偏离,先是向上偏离,然后向下偏离,导致在顶进50 m时出现较大应力波动。在直线段L2和曲线段S2,顶管机均向下偏离轴线,原因是向上纠偏使管顶外侧受到拉应力,内侧受到压应力,而管底内外均受拉。

图10 管顶纵向应力随顶进距离的变化曲线Fig. 10 Variation of longitudinal stress at pipe top with jacking distance
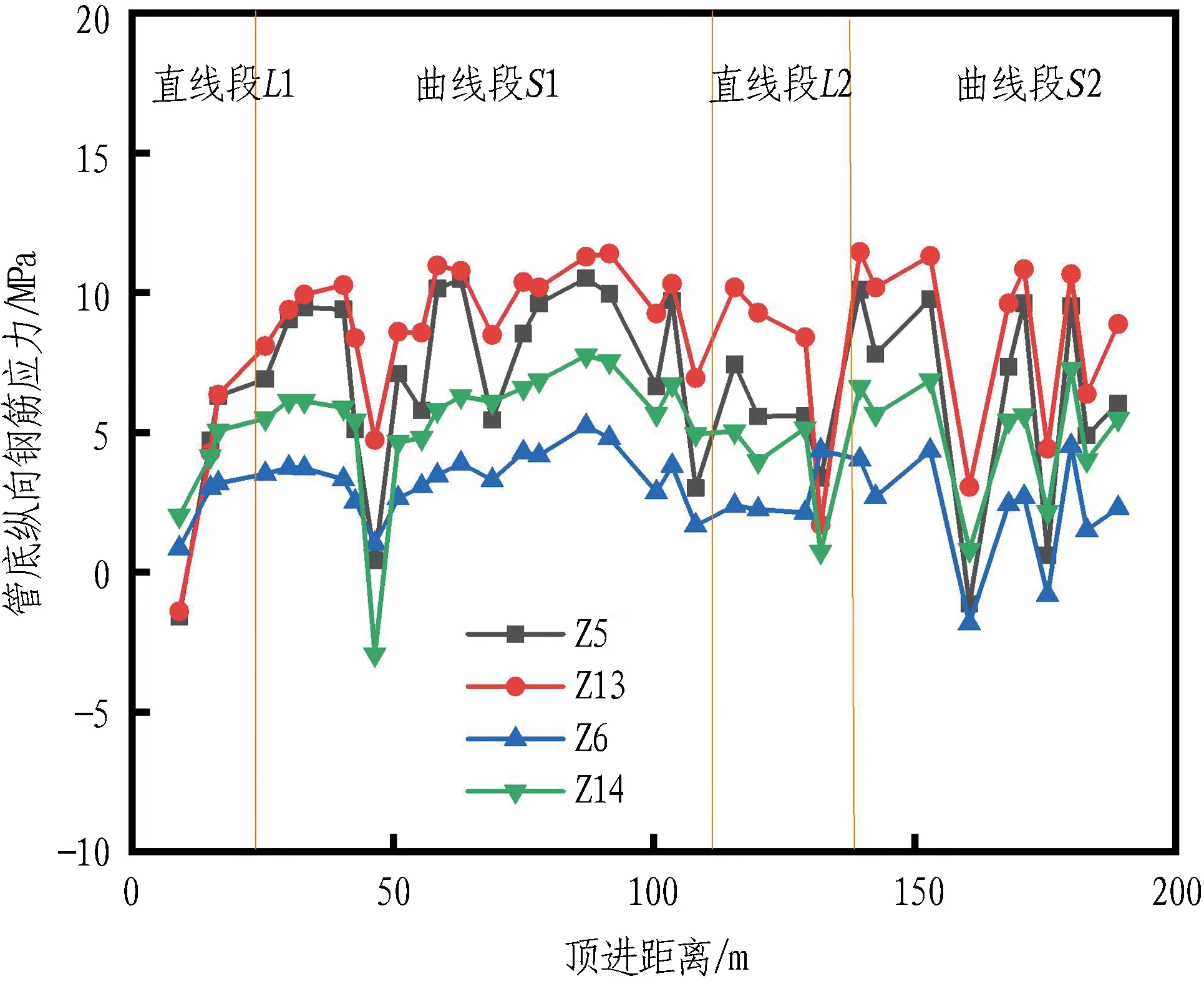
图11 管底纵向应力随顶进距离的变化曲线Fig. 11 Variation of longitudinal stress at pipe bottom with jacking distance
管腰左侧和右侧纵向应力随顶进距离的变化曲线分别如图12和图13所示。由图可知,在水平方向上,管腰两侧钢筋应力主要在-15~15 MPa波动,在S型曲线顶进施工过程中,千斤顶力通过顶铁向管道作用纵向均布荷载,在纵向荷载作用下,管道外侧应力明显增加,即管腰外侧主要受到拉应力,内侧主要受到压应力。在S型曲线段顶进时,管道水平纠偏使管口存在挤压和张角现象,钢筋混凝土管道存在受力敏感性,即纵向荷载略有变化将导致管道应力出现波动。在曲线段S1向右转向,管口左侧存在张角,管腰左侧数据平稳,管口右侧存在挤压,挤压处受加载和卸载影响较大,管腰右侧数据波动。同理,在曲线段S2则相反。在整个S型曲线段上的受力变化情况关于直线段L2对称。

图12 管腰左侧纵向应力随顶进距离变化Fig. 12 Variation of left longitudinal stress at pipe with jacking distance
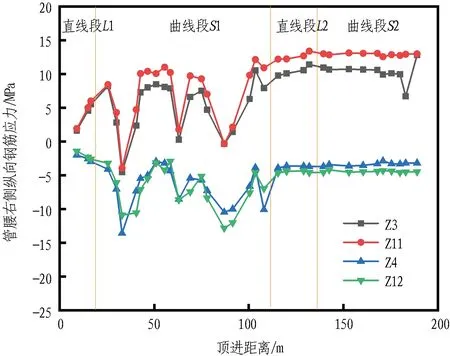
图13 管腰右侧纵向应力随顶进距离变化Fig. 13 Variation of right longitudinal stress at pipe with jacking distance
据分析可知,纵向钢筋应力主要受顶力影响,但S2曲线段顶力增加1 000 kN,钢筋应力增加不明显,可反映出顶力增加量很适用、减摩效果良好。顶进轨迹偏差使管道应力集中,在偏心受力状态下,管壁向外不均匀膨胀变形,变形大致如图14所示。管道受拉侧容易发生破坏,设计时需要进行强度验算。实际施工中,管道受到的拉应力小于混凝土抗拉强度,表明管道结构安全性较好。
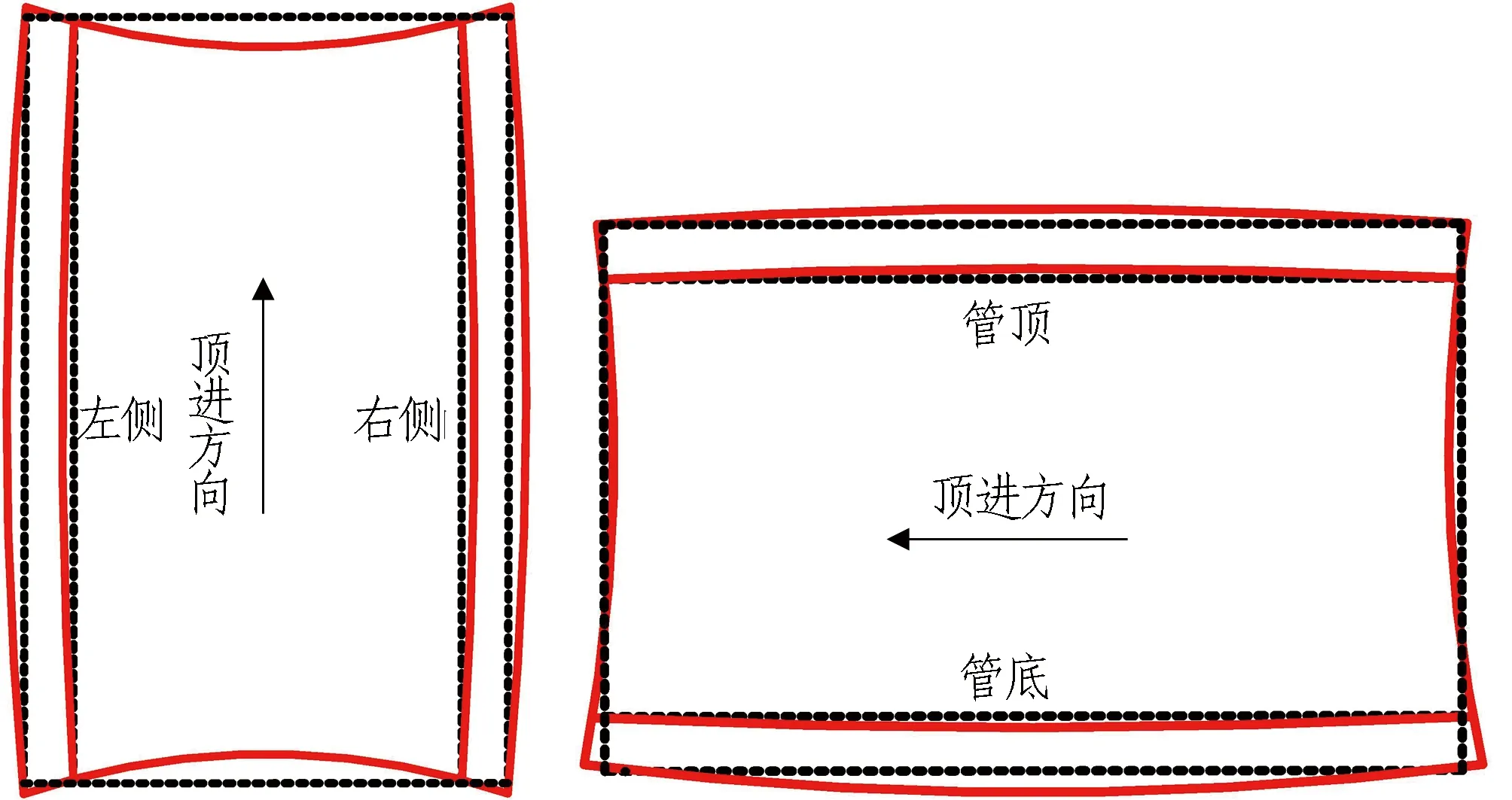
图14 管道变形图Fig. 14 Pipe deformation
2.2 管土接触应力分析
管道与土体之间的接触压力与管道内力数据同步采集,管土接触应力随顶进距离的变化规律如图15所示。由图15分析可知,管道进洞后,土体释放的压力全部作用在管壁上,管土接触应力急剧增加至0.13 MPa,管道顶进20 m后开始进入S1曲线,同步注浆量为1.5 m3,注浆压力为0.15 MPa,减摩泥浆可对土体起到一定的支护作用,实际注浆压力和环向土压力的不稳定性使得管土接触应力开始波动。进入S2曲线后,同步注浆量为3 m3,注浆压力为0.2 MPa。管土接触应力随着同步注浆量、注浆泵压力、管道埋深的增加而增加,管土接触应力最大值为0.17 MPa。

图15 管土接触应力变化规律Fig. 15 Variation law of pipe-soil contact stress
顶管机进入S1曲线段后,由于人工关闭注浆阀门不及时导致注浆量过多,在70~110 m有膨润土上渗至地表的现象,采取减小同步注浆量和增加顶进速度至55 mm/min的措施快速通过漏浆段,导致此段的管土接触应力有所变化,分布更为均匀。在S1曲线段大幅度纠偏增大了刀盘对土体的扰动,使略大于开挖直径的土体受到重力作用而脱落,从而管土间存在一定的空隙。顶管机在S1曲线段向右偏离轴线,最大偏离值达到80 mm,机头向左大幅度纠偏导致后续管道偏离轴线向右滑移。进入S2曲线后仍然存在向右滑移现象。管道处在饱和的泥浆套中,管道自重大于泥浆托浮作用,在整个曲线段管道一直沉在泥浆套的右下方,如图16所示,管道右侧管土空隙小于管道左侧。在同步注浆过程中,管道左侧注入更多的泥浆,产生更大的接触应力,致使管道左侧管土接触应力值偏大。因此,在整个S型曲线段上管土接触应力大小为: 管道左侧>管底≈管顶>管道右侧。
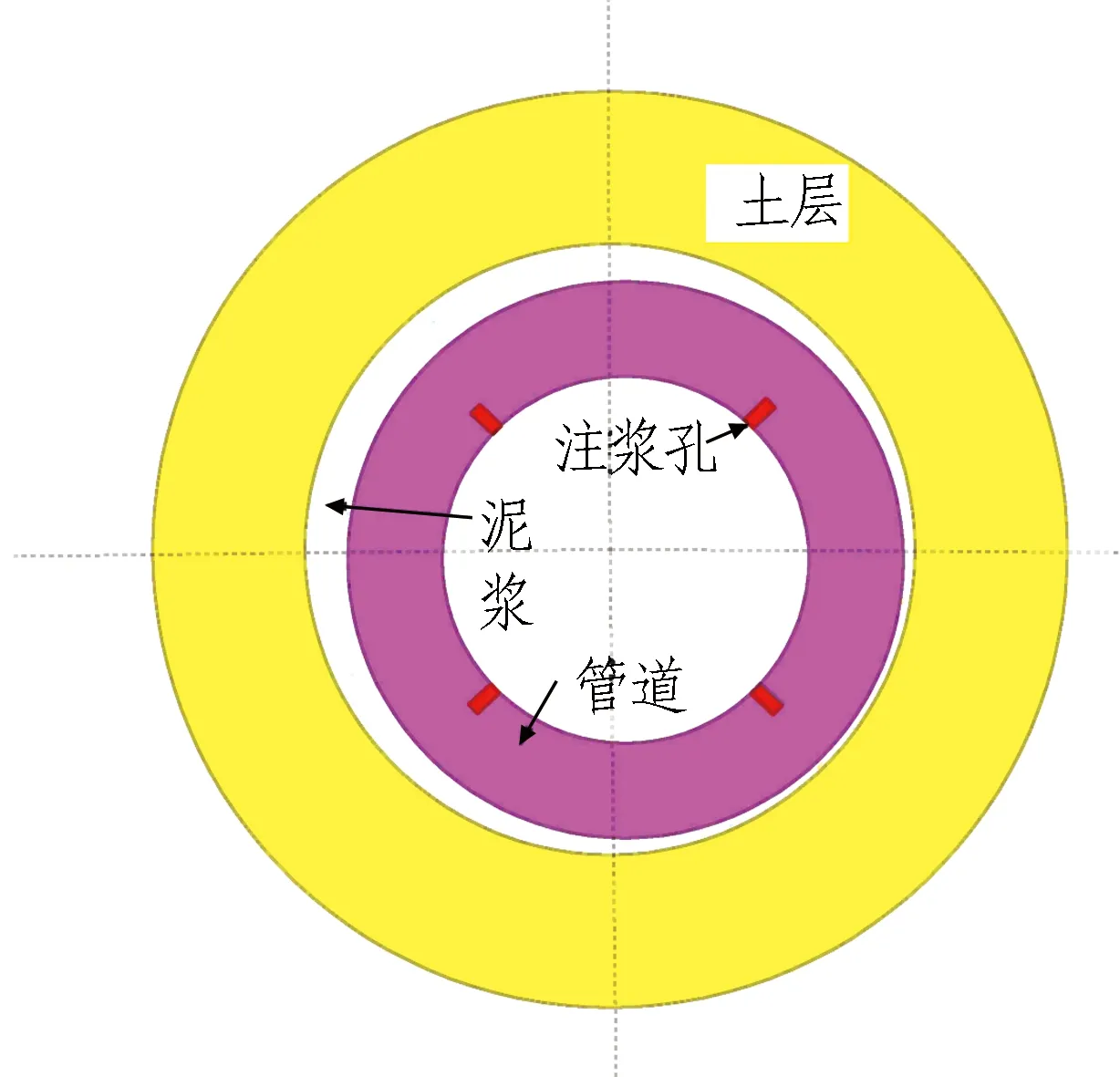
图16 管土接触状态Fig. 16 Pipe-soil contact state
结合现场施工情况分析,管土接触应力波动原因为: 注浆阀门有时处于关闭停顶状态或打开注浆状态导致注浆压力变化;随着管道以0.99%的坡度向下顶进,管壁覆土重度变大,水土压力变化;管周土体随开挖扰动后跌落至管壁上并稀释减摩泥浆;管道上方车辆荷载对地表下土体扰动;实际施工状况等。其中,注浆压力占主导因素。
3 管道应力数值模拟验证与拓展分析
3.1 建立模型
采用有限元软件Midas GTX NX进行模拟,并与实测数据进行对比验证。以管道中心为坐标原点,管道顶进方向为Y轴正方向,土层厚度为Z轴方向,管道计算模型尺寸为外直径R=4.14 m,内直径r=3.5 m,壁厚t=0.32 m。根据圣维南原理和相关工程模型,考虑土体开挖对周边土体的影响将延伸5倍,计算模型尺寸为190 m×102 m×19.6 m,如图17所示。管道覆土埋深H=8.68 m,隧道位置与土层分布如图18所示。模型边界设置位移约束,限制X、Y、Z3个方向的自由移动。模型受力除自重以外,还依照现场施工荷载设置有200 kPa的千斤顶力、150 kPa的注浆压力、2 kPa的侧摩阻力、120 kPa的泥水舱压力。由于无法模拟纠偏措施,管道顶进轴线按设计S型空间曲线建立,模型施工步骤按实际施工工序设置。模型参数见表1。
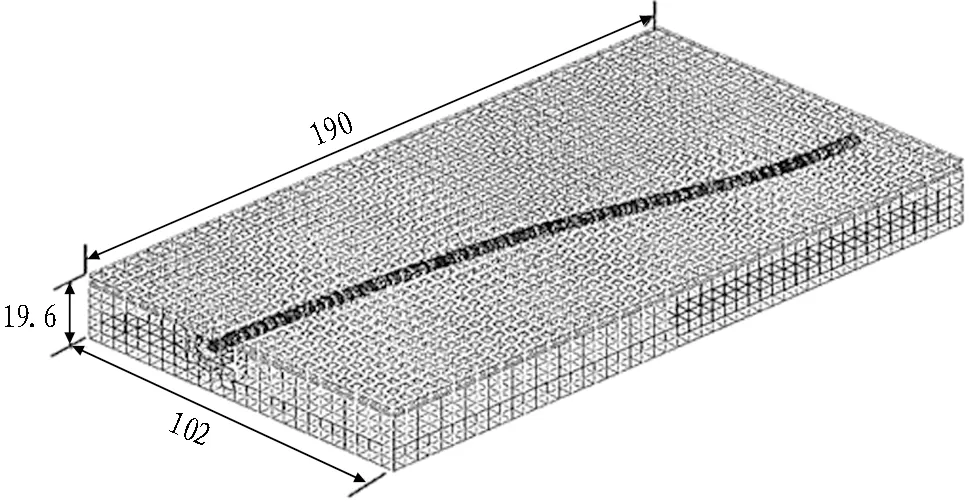
图17 模型尺寸(单位: m)Fig. 17 Model dimensions (unit: m)
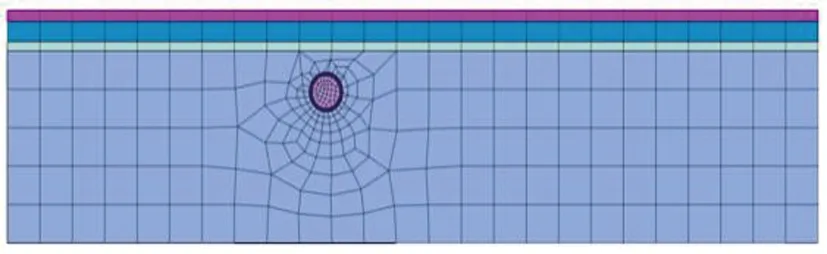
图18 隧道位置与土层分布图Fig. 18 Tunnel location and soil layer distribution
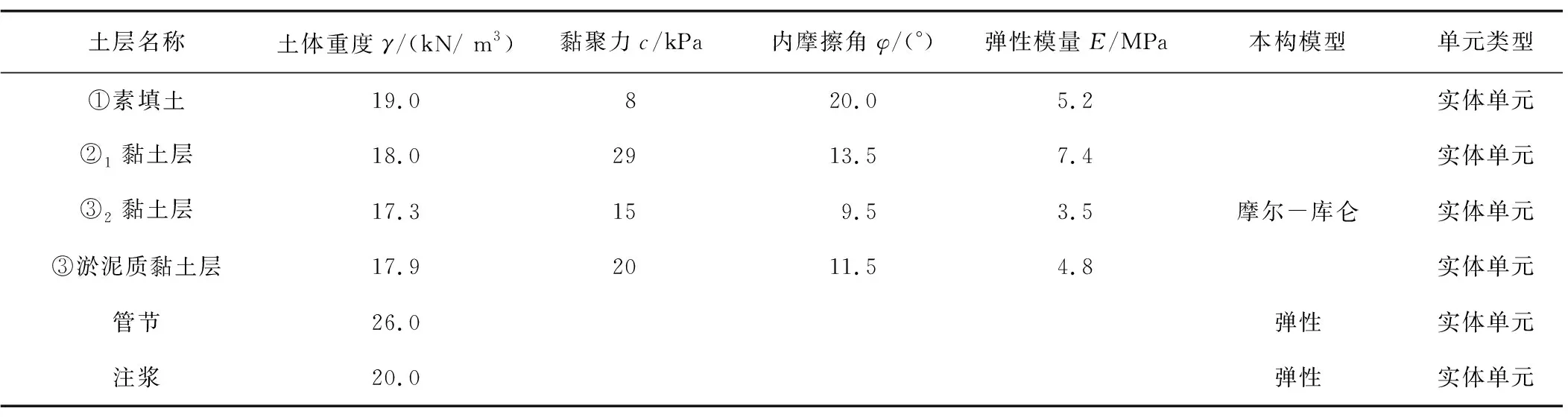
表1 模型参数Table 1 Model parameters
3.2 模拟结果分析
对应实测数据选取具有代表性的曲线S1漏浆段第60号管道和曲线S2中第110号管道作为研究对象,2段曲线中剩余管道应力分布也与之相似。2个管道处管土接触应力云图如图19和图20所示。由图可知,曲线段S1管壁接触应力分布为管道左侧>管底>管顶>管道右侧;曲线段S2管壁接触压力分布为管底>管道左侧>管顶>管道右侧。由于模拟施工中无法体现实时注浆效果,只能在等待层的法向上同时施加均布的环向压应力,模拟中的应力值变化没有实际中剧烈。数据表明,管道四周压力大小不等,管道受力不均匀、不对称,这与实测数据相符。
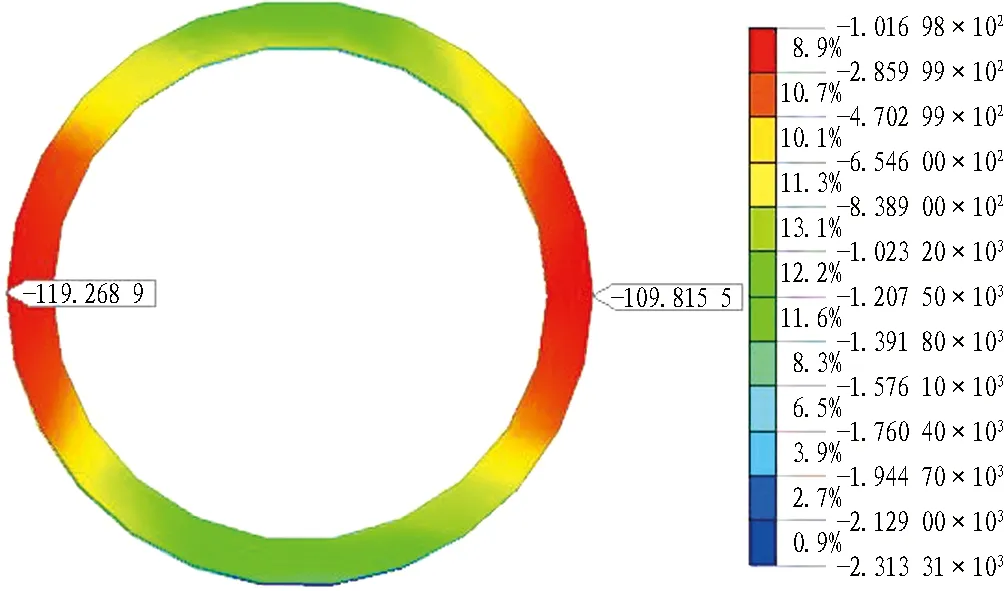
(a) 水平接触应力
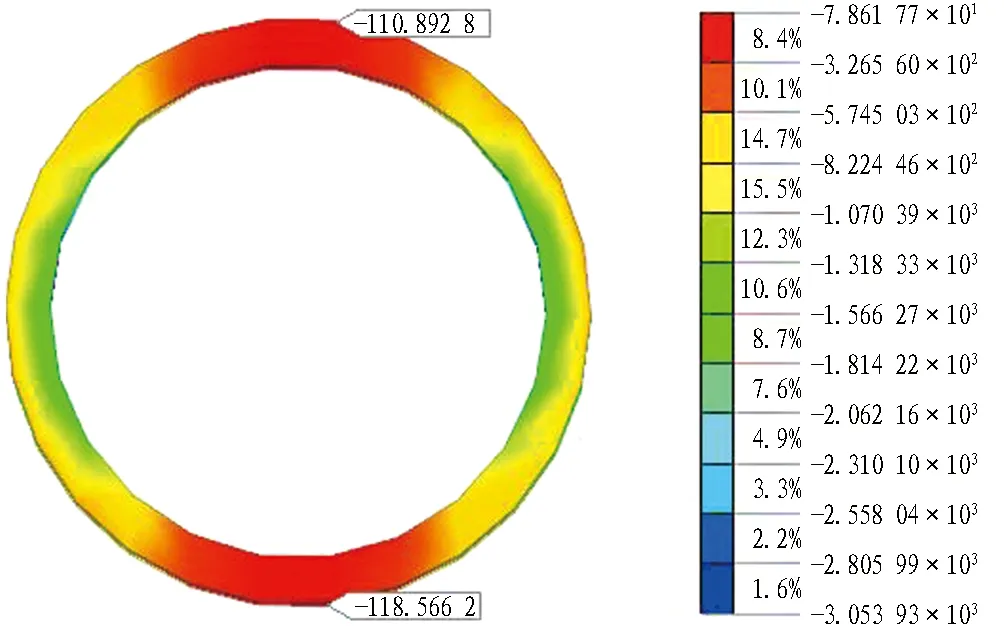
(b) 竖向接触应力图19 60号管道管土接触应力云图(单位: kPa)Fig. 19 Nephograms of contact-stress of pipeline No. 60 (unit: kPa)
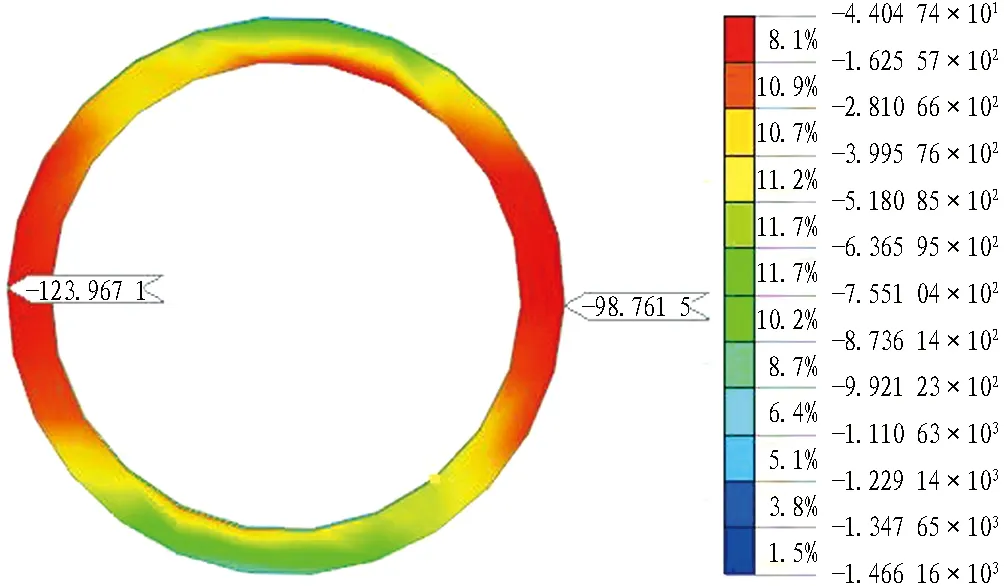
(a) 水平接触应力
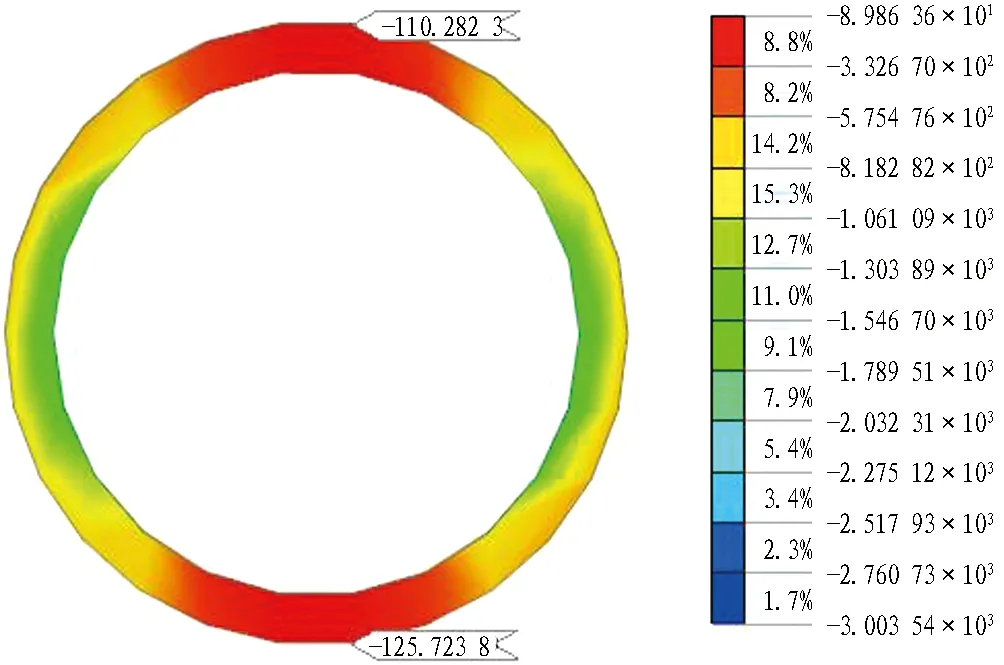
(b) 竖向接触应力图20 110号管道管土接触应力云图(单位: kPa)Fig. 20 Nephograms of contact-stress of pipeline No. 110 (unit: kPa)
提取管道弯矩云图(见图21)的数据作管道弯矩数据图,见图22。图22中,管道左侧弯矩值为92.2 kN·m,管道右侧弯矩值为81.5 kN·m,左侧略大于右侧;管壁弯矩图中呈现出管腰受压,管顶管底受拉,也与管道环向“横鸭蛋状”的形变相符。
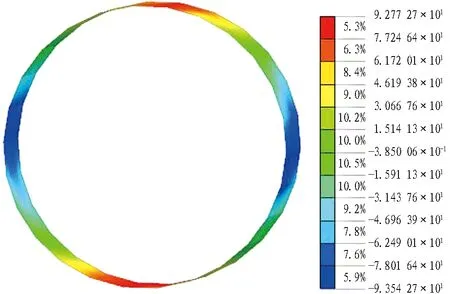
图21 管道弯矩云图(单位: kN·m)Fig. 21 Nephogram of bending moment of pipe (unit: kN·m)
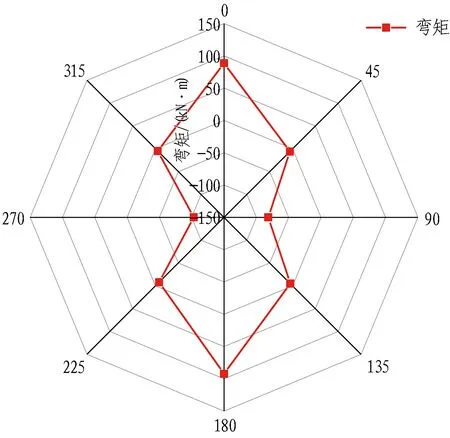
图22 管道弯矩数据图Fig. 22 Bending moment diagram of pipe
管土接触应力实测与模拟值的对比见图23。由图可知,两者管土接触应力值存在明显差异。这是由于管道在实际施工过程中,管土相互作用不仅受到注浆压力和土压力的影响,还受到管道纠偏、注浆渗漏、管道位移、突发施工状况、地层损失、挤土效应、土拱效应等影响,因此模拟数据与实测数据存在偏差。管道节数和对应数据不连续导致模拟数据波动,但比实测数据更为平稳,模拟结果呈现出与实际S型曲线顶管相似的管壁接触应力变化规律。管顶与管底受转弯影响较小,应力值相近;管腰受转弯影响较大,应力值存在较大差异。
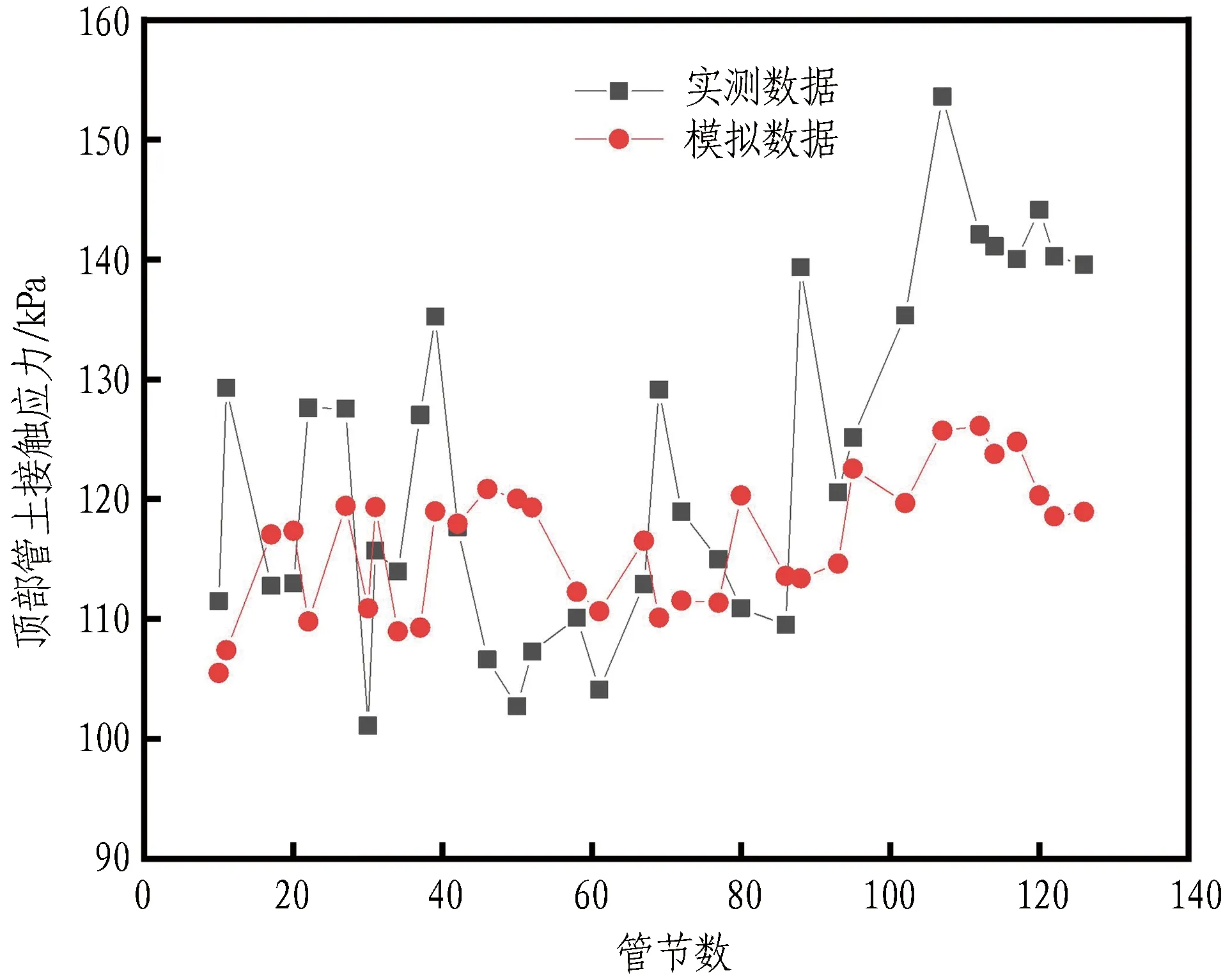
(a) 管顶

(b) 管底
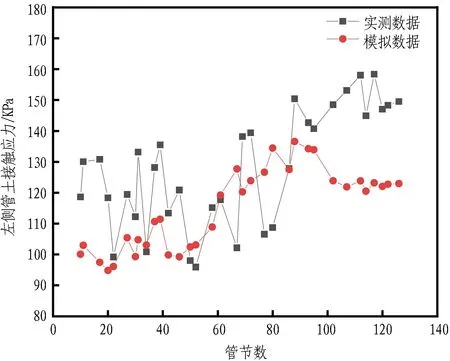
(c) 管道左侧
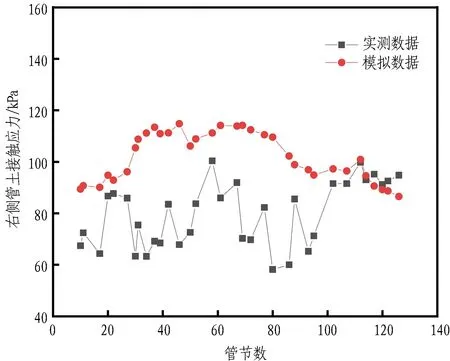
(d) 管道右侧图23 实测数据与模拟数据对比Fig. 23 Comparison between measured and simulated data
3.3 不同影响因素下管土受力分析
为研究不同影响因素下管道的受力情况,选取4种主要影响因素进行模拟分析,将根据《顶管工程施工规程》[17]和《给水排水管道工程施工及验收规范》[18]中的取值范围建立4个工况组,每组工况在原模型上分别以管道埋深、注浆压力、平曲线半径、千斤顶顶力为单一变量进行拓展模拟。原模型参数管道埋深设为8.65 m,注浆压力为150 kPa,平曲线半径为500 m,千斤顶顶力为200 kPa。各工况组不同影响因素取值见表2。

表2 不同工况组影响因素取值Table 2 Working conditions
在各工况组中,提取同一位置管道应力的模拟结果作图,分析不同影响因素取值条件下曲线顶管管道横截面受力情况,即管壁应力和管道纵向应力的分布情况。
3.3.1 管道埋深
管壁应力与埋深关系见图24。分析结果表明,管壁应力值随管道埋深的改变而变化,这种变化幅度在管顶和管底尤为显著。针对埋深大、坡度大的顶管工程,管道设计时可考虑加强管顶和管底的钢筋布置。

图24 管壁应力与埋深的关系Fig. 24 Relationship between pipe wall stress and buried depth
3.3.2 注浆压力
管壁应力与注浆压力关系见图25。由图可知,曲线顶管的管壁应力往往是不均匀、不对称的。若适当增加注浆压力,可缓解管道受力不对称、不均匀现象,避免管道受到集中应力而出现局部破坏,或通过改变局部注浆压力达到管道微纠偏的效果。
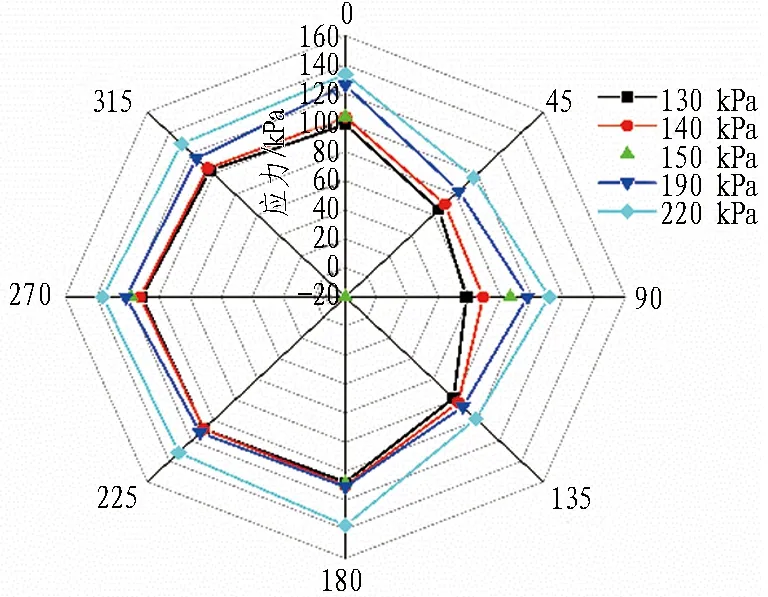
图25 管壁应力与注浆压力的关系Fig. 25 Relationship between pipe wall stress and grouting pressure
3.3.3 平曲线半径
管壁应力与平曲线半径关系见图26。由图可知,由于挤土效应的存在,平曲线半径越小时,管壁应力分布越不均匀,管道应力越集中,管道变形越大,所以水平纠偏时纠偏程度不宜过大,避免产生平曲线半径过小、管道应力集中的现象。
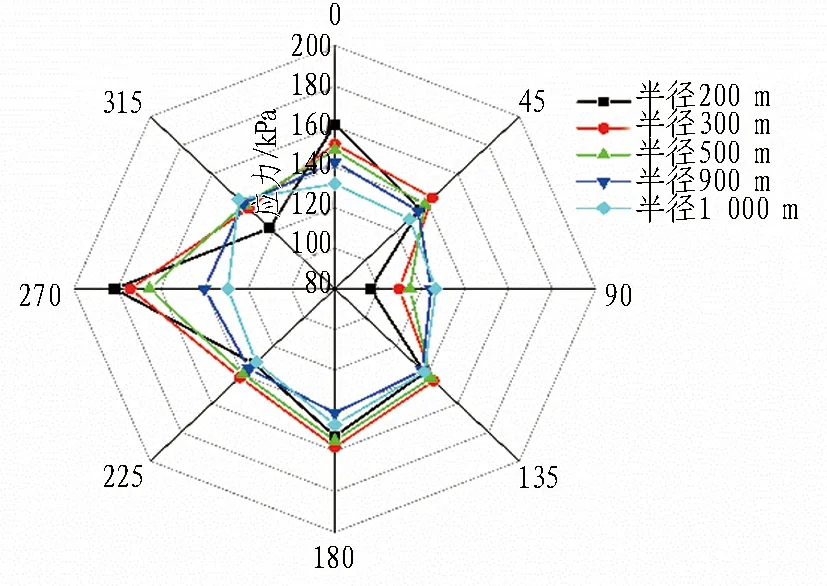
图26 管壁应力与曲线半径的关系Fig. 26 Relationship between pipe wall stress and horizontal curve radius
3.3.4 顶力与管道纵向应力关系
管道纵向应力与顶力关系见图27。由图可知,曲线顶进过程中,管道会出现滑移和偏转现象,管道受到偏心荷载,使纵向钢筋应力分布不对称。增加千斤顶顶力,不会使应力重分布,只会使管道纵向应力更加集中。
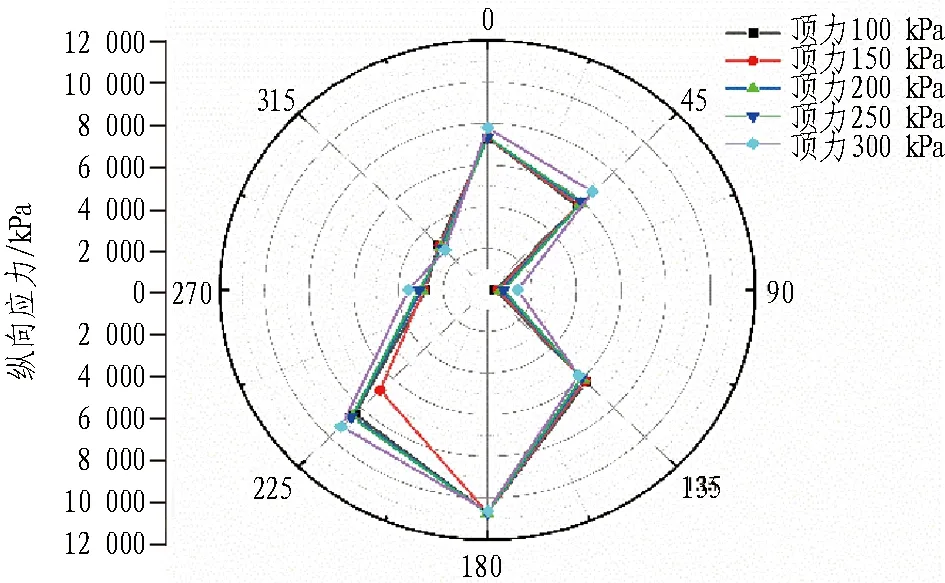
图27 管道纵向应力与顶力的关系Fig. 27 Relationship between longitudinal stress and jacking force of pipeline
4 结论与建议
基于对大直径长距离S型空间曲线顶管顶进过程中管道受力的研究,分析了管道钢筋应力的变化规律以及施工参数对管道应力的影响,将三维数值模拟结果进行对比,同时建立多组工况分析管道在不同情况下的受力状态,得出以下结论。
1)管道环向钢筋应力受转向影响不大,主要受注浆压力和施工方式影响。在整个S型曲线段,管顶和管底外侧受拉应力,内侧受压应力,管腰则相反,管腰内侧钢筋应力略大于外侧。在不均匀、非对称的受力状态下,管道呈现出“横鸭蛋”状变形;管道纵向钢筋应力主要受顶力和顶进轨迹影响。在2段反向曲线段上,管腰两侧纵向钢筋应力交替波动,“磕头”与大幅度向上纠偏使管底受拉应力,其余部位外侧受拉应力、内侧受压应力。在偏心受力状态下,管道结构安全性仍较好。
2)由于曲线转向产生超挖间隙和管道滑移,管道自重大于泥浆托浮作用,使管道在整个S型曲线段均处在泥浆套的右下方,受不均匀注浆压力影响,管土接触应力大小为管腰左侧>管底≈管顶>管腰右侧。
3)三维数值模拟结果中管道所受应力大小与实测结果存在差异,但模拟结果呈现出与实际S型曲线顶管相似的管壁接触应力变化规律。管顶与管底受转弯影响较小,应力值相近,管腰受转弯影响较大,应力值存在较大差异。针对大直径长距离S型空间曲线顶管工程,在不同工况下的模拟结果为: 管道埋深和坡度较大时,管顶和管底管壁应力变化尤为显著;适当增加注浆压力,可缓解管壁应力不对称、不均匀现象;水平纠偏时纠偏程度不宜过大,避免平曲线半径过小产生管道应力集中的现象;增加顶力不会使纵向应力重分布,只会使应力小幅度增加。
本工程数据较多,环向应力、管土接触应力所呈现的S型曲线顶管特有规律性不明显,有关应力分布特征有待进一步研究。若数值模拟采用每节管道施加实时工况的精细化模型,模拟结果会更具参考价值。

