井筒式基坑开挖变形特性及稳定性分析
李红军, 冷 远, 张士龙, 刘昌永
(1. 中交二航局第三工程有限公司, 江苏 镇江 212000; 2. 哈尔滨工业大学, 黑龙江 哈尔滨 150000)
0 引言
随着我国城市化进程的不断推进,交通拥堵问题日益突出,市区停车难问题亟待解决。由于井筒式地下车库具有空间利用率高、环境适应性强、结构布置灵活等优点,近几年逐步应用于城市停车场建设中[1-2]。井筒式地下车库多由圆形基坑和与围护结构相连的楼板组成,支护形式通常采用排桩加圈梁体系[3]。
由于井筒式地下车库结构的复杂性,近几年国内学者对井筒式地下车库进行了一系列的研究。吴金锋[4]为推广井筒式地下停车场,以2016年国内首次修建的杭州某井筒式地下停车场为例,从停车规模、周边交通影响、社会影响和项目经济性4方面论述了井筒式地下停车场的应用前景。王栋等[5]介绍了杭州地区开挖深度为34.3 m的井筒式地下车库基坑施工中所涉及的工艺工法。张创[6]以成都地区砂卵石地层修建井筒式车库为例,利用FLAC3D对其进行数值模拟,通过改变排桩桩长、桩端嵌固条件、基坑大小等参数,研究基坑受力和变形的情况; 同时,在施工和使用阶段对车库主体结构进行了受力分析,最后给出了井筒式车库相应的设计参数。
通过上述研究可见,对于井筒式地下车库的研究主要集中在以砂卵石地层为主的南方地区,缺乏东北地区黏性土层下修建井筒式地下车库的相关研究。同时,为满足地下停车场智能化的要求,通常在基坑内部进行二次土体的开挖,导致基坑底部被动区域土体抗力的减弱,从而对基坑稳定性造成影响[7]。为此,本文以哈尔滨省委广场井筒式智能停车场为工程背景,对井筒式基坑围护结构的受力和变形进行分析,同时研究二次开挖对基坑稳定性的影响。
1 项目概况
哈尔滨省委广场位于南岗区花园街与吉林街交口,拟在现广场地下空间建设井筒式智能停车场,外径为22 m,开挖深度为13.2 m。地下停车场主体结构采用钢筋混凝土框架,基坑围护结构采用排桩+圈梁支撑体系,桩间挂网喷厚度为80 mm的C20混凝土。为放置井筒式智能停车场机电设备,在基坑中设置深度为2.4 m的坑中坑,如图1所示。

(b) 剖面图(单位: m)图1 井筒式停车场布置图Fig. 1 Layout of shaft-type parking lot
在基坑周围共布置了5个钻孔来勘察地质情况,根据勘察结果,场地所处地貌为岗阜状平原,地基土分布不均匀。施工场地区间位于岗阜状平原地貌中,勘察孔隙潜水稳定水位标高为-28.5~-33.2 m,地下水始终位于开挖面以下,可不考虑开挖过程中水位变化的影响。
2 井筒基坑的监测
2.1 监测方案
根据工程周围环境的情况,依据规范对基坑进行监测。本节内容是在井筒内部土体被挖除期间对施工引起的沉降等相关项目进行监测,基坑监测点布置和监控项目分别如图2和表1所示。

图2 基坑监测点布置图Fig. 2 Layout of monitoring points of foundation pit

表1 基坑监控项目Table 1 Monitoring items of foundation pit
根据勘测和设计资料制定工程进度计划表。本井筒基坑共分4次开挖,除表层杂填土开挖外,后续开挖均处于软黏土层,如表2所示。

表2 施工阶段Table 2 Construction conditions
2.2 地表沉降
井筒基坑北部紧邻居民楼,南部紧邻道路(见图2),故选取基坑北部一排地表沉降测点DB1、南部一排地表沉降测点DB2。地表沉降值随时间变化曲线如图3所示。图3(a)中测点DB1-3距离基坑水平位置为5 m,在整个开挖过程中累计最终沉降为4.8 mm; 测点DB1-2距离基坑水平位置为10 m,在整个开挖过程中累计最终沉降为4.1 mm; 测点DB1-1距离基坑水平位置为20 m,此处测点位于居民住宅区附近,累计沉降变化不大,表明井筒基坑开挖对居民楼无影响。图3(b)中基坑南部测点DB2-2、DB2-3,15 d后沉降值达到稳定,分别为9.8、11.6 mm。由于场地空间有限,基坑西侧为施工出土和设备堆放区,基坑南侧为挖机停留区域,因此基坑南部测点与基坑北部测点相比沉降较大。

(a) 测点DB1累计沉降曲线

(b) 测点DB2累计沉降曲线图3 地表沉降值随时间变化曲线图Fig. 3 Curves of surface subsidence changing with time
2.3 围护桩深层水平位移
由于基坑南部受来往车辆影响,故选取基坑南部测斜管CX1作为分析对象,施工工况如表2所示。测斜CX1深度-位移变化曲线如图4所示。由图可知: 在不同工况下测斜管CX1整体趋势为“鼓肚”形状,最终侧移值为3.5 mm,远远小于控制值,表明圆形支护结构的空间“拱效应”得到了充分的发挥,并没有受到南部地表沉降的影响。工况2为基坑开挖深度6.9 m的情况,最大侧移值位于桩体深度4 m处,为1.2 mm; 工况3为基坑开挖深度11 m的情况,最大侧移值位于桩体深度6.3 m处,为3.2 mm; 工况4为基坑开挖深度13.4 m的情况,最大侧移量位于桩体深度6.3 m处,为3.5 mm。随着基坑开挖深度的增加,最大侧移位置逐渐向下移动。
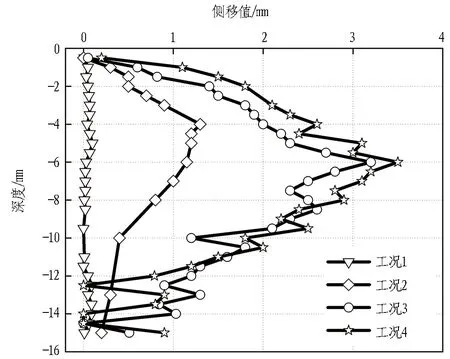
图4 测斜CX1深度-位移变化曲线图Fig. 4 CX1 depth-displacement curves
3 井筒基坑数值计算模型
3.1 有限元模型的建立
利用大型有限元软件MIDAS/GTS建立井筒基坑的三维模型。根据基坑开挖影响范围,数值模型的整体尺寸为160 m×160 m×30 m(长×宽×高)。土体采用修正摩尔-库仑模型,结构单元采用线弹性模型。根据地勘报告及相关经验取值,土层及结构的力学参数如表3和表4所示。土体采用实体单元,冠梁和排桩均采用梁单元模拟[8]。模型四周约束各面的法向位移,底部约束3个方向的位移,荷载主要考虑土体及结构的自重荷载。井筒基坑三维模型如图5所示。
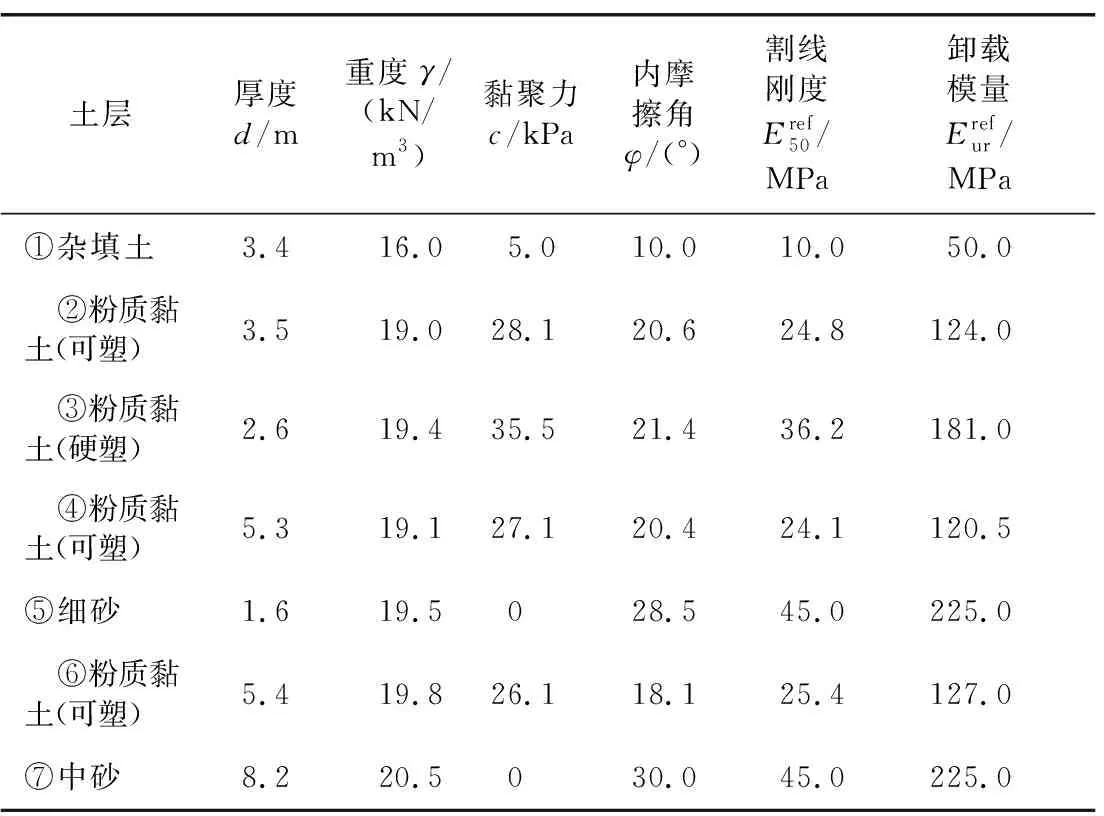
表3 土层力学参数Table 3 Soil mechanical parameters
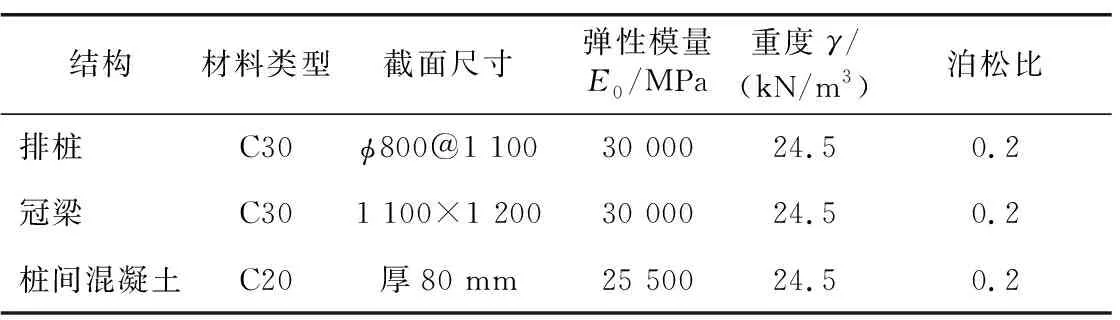
表4 结构力学参数Table 4 Structure mechanical parameters
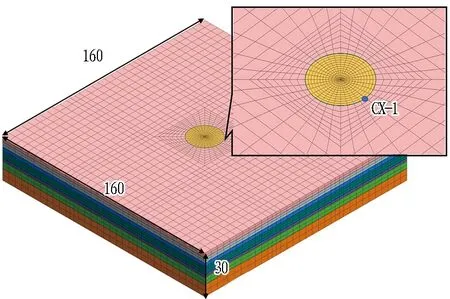
图5 井筒式基坑三维模型(单位: m)Fig. 5 Three-dimensional model of shaft-type foundation pit (unit: m)
3.2 有限元模型的验证
结合2.3节围护桩水平变形的监测数据,对比MIDAS/GTS数值计算结果,以验证数值计算结果的正确性。有限元数值模拟计算中井筒基坑内土体被挖除的模拟进尺与施工阶段(见表2)一致。有限元分析桩体水平位移时选取的是基坑南部测点CX-1,如图5所示。数值计算与监测值对比如图6所示。由图可知,MIDAS/GTS计算的围护桩最大侧移值为4.15 mm,监测值为3.5 mm,两者均在深度6.3 m处桩体水平位移达到最大,有限元计算结果与实际情况较为符合。从曲线的整体趋势上来看,两者都呈现出“两头小,中间大”的变形特点,数值计算曲线光滑、平顺,实测曲线不平顺,数据存在一定程度的离散。究其原因,主要是在有限元分析时采用了诸多假设,例如将土体按各向同性、均匀材质模拟,故计算结果与实测值存在一定差异。

图6 数值计算与监测值对比Fig. 6 Comparison between numerical calculation and monitoring value
3.3 井筒基坑环向拱效应分析
3.3.1 拱效应分析
井筒基坑开挖时土压力拱的形成,主要为环向和竖向拱效应。井筒挡土结构径向移动过程中,环向拱效应发挥先于竖向拱效应[9]。考虑到井筒基坑尺寸小,且实测位移小,本节主要对环向压力拱的形成过程及分布规律进行详细分析。
轴对称井筒基坑是柱坐标下的平面问题,只在径向平面内产生变形。开挖时土压力拱的形成,主要是由于水平面内中主应力与小主应力的方向调整,由中主应力在基坑环向形成连续封闭的压力路径。土压力拱的形成有利于基坑的稳定,其形成过程与开挖工况息息相关。由于基坑地质条件以粉质黏土为主,因此取地表下6.9 m深度网格组为观测面。
观测面上中主应力矢量图如图7所示。为方便对比各个开挖工况下井筒周边拱效应变化,隐藏了图7(a)中基坑内部的土体单元。1)在基坑开挖之前(见图7(a)),观测面上任意一点的小主应力为自重应力σz=γz(γ为土的天然重度,z为土的厚度),中主应力则为-92.80 kPa(σx=σy=K0γz,σx为x方向应力,σy为y方向应力,K0为侧应力系数),沿深度呈线性关系。即初始未开挖状态下,作用于挡土结构两侧的土压力计算值与公式计算值一致,不存在环向拱效应。

(a) 开挖前

(b) 工况1
(c) 工况2

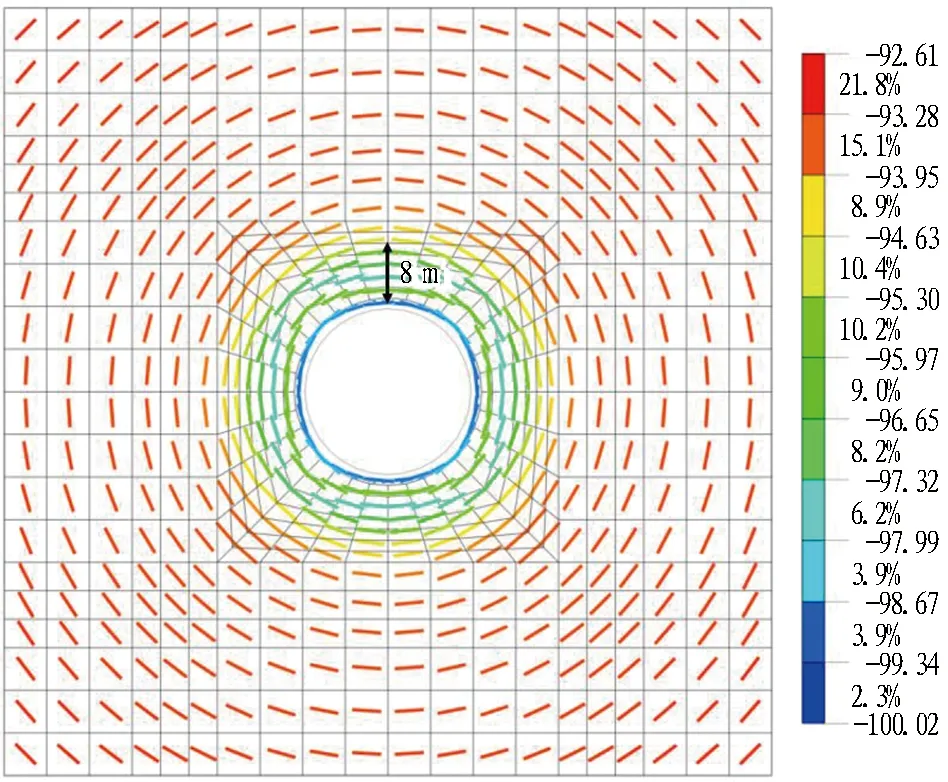
(d) 工况3图7 观测面上中主应力矢量图(单位: kPa)Fig. 7 Vector diagram of medium principal stress on observation surface (unit: kPa)
2)在基坑开挖工况1完成后(见图7(b)),观测面的表层土体被挖除,围护结构已发生一定的径向变形,引起土体应力重分布,对应观测面位置的中主应力最大值略有增加(-95.05 kPa)。从整体应力矢量图来看,初步形成连续、封闭的环向传力路径。
3)在基坑开挖工况2完成后(见图7(c)),观测面以上的土体被完全挖除,围护结构后方土体变形进一步增大,中主应力数值随距离坑边的远近不同呈现出不同程度的增大,在近基坑开挖面处增幅明显,较远处增加较小并逐步趋于初始值。中主应力的环向影响范围进一步扩大,表明拱效应的作用程度逐步增强,基坑观测面处受开挖影响的环向压力拱已形成。
4)在基坑开挖工况3完成后(见图7(d)),随着观测面下方的土体被挖除,围护结构位移进一步增大,中主应力在靠近围护结构处均小于初始环向应力值,随着距坑边距离的增大,其应力值先增大后减小,再趋于初始中主应力。
综上所述,圆形基坑的环向拱效应,可以采用土体的中主应力矢量图进行表达。随着基坑开挖深度的逐步增大,其环向拱效应作用的土体范围也逐步扩大。
3.3.2 中主应力变化分析
为进一步探究中主应力影响范围的大小,绘制不同开挖阶段距坑边不同距离的土体中主应力变化曲线,如图8所示。

(a) 距坑边0.7 m
(b) 距坑边3.0 m
(c) 距坑边8.0 m
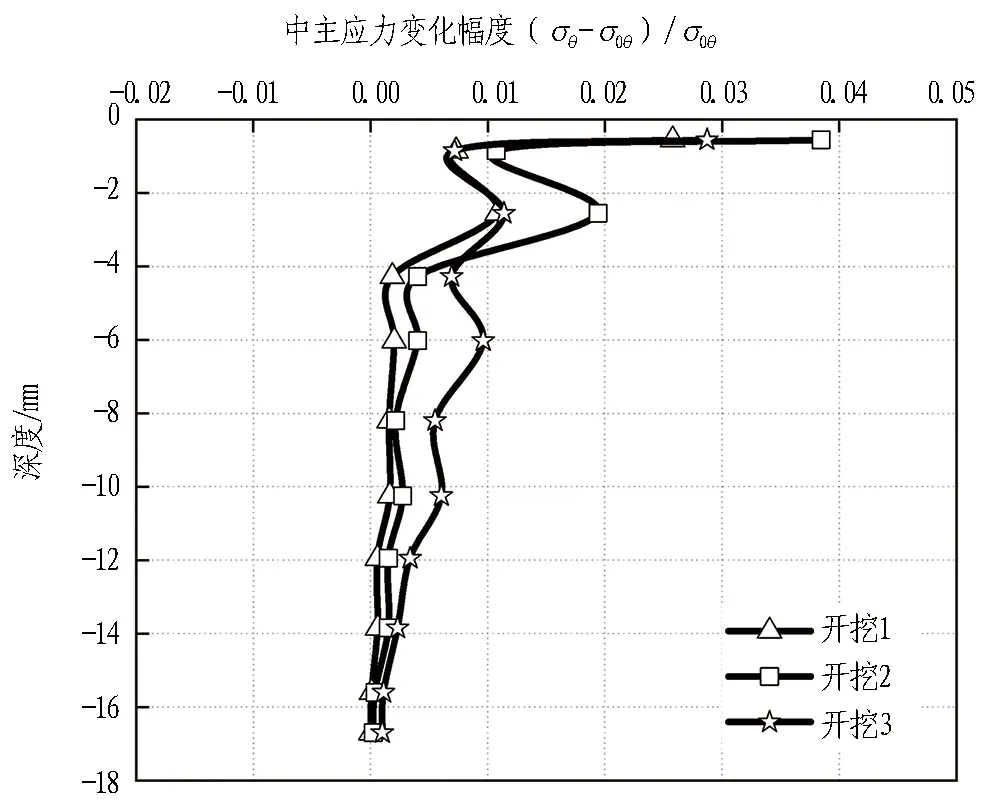
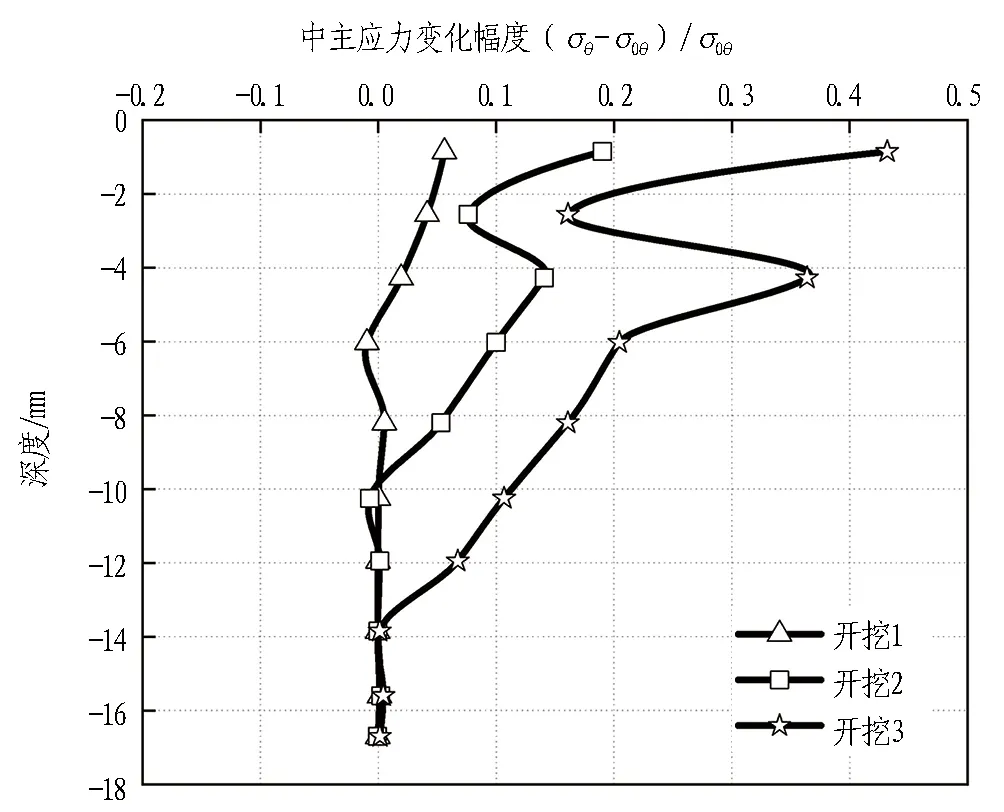
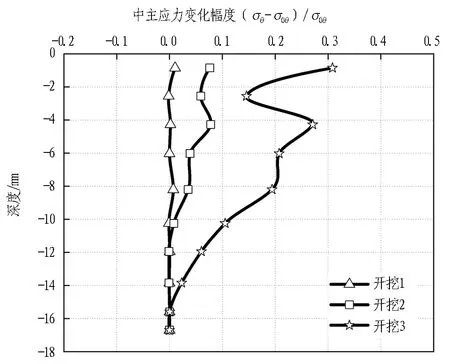
(d) 距坑边12.0 m图8 不同开挖阶段距坑边不同距离中主应力变化曲线Fig. 8 Variation amplitude distribution curves of medium principal stress at different distances from pit edge in different excavation stages
基坑开挖前中主应力为σ0θ,基坑开挖后中主应力为σθ,基坑开挖前后中主应力变化幅度为(σθ-σ0θ)/σ0θ。由图8(a)可知,不同开挖阶段中主应力表现为负的增量,是土方开挖卸载导致的。由图8(b)—(d)可知,随着距坑边距离增大,中主应力值随着基坑逐步开挖均表现为正的增量,且增幅逐渐变缓。当距坑边12 m时,其增量基本可以忽略不计。
其中,基坑在开挖1工况下,由图8(b)可知,距坑边3 m时中主应力最大变化幅度为6%; 由图8(c)可知,距坑边8 m时中主应力最大变化幅度为1%,中主应力变化幅度随着基坑的距离增加逐渐减弱。因此,开挖1引起的拱效应范围为距坑边3 m。
基坑在开挖2工况下,由图8(b)可知,距坑边3 m时中主应力最大变化幅度为19%; 由图8(c)可知,距坑边8 m时中主应力最大变化幅度为8%,中主应力变化幅度随着基坑距离的增加逐渐减弱。因此,开挖2引起的拱效应范围为距坑边8 m。
基坑在开挖3工况下,由图8(b)可知,距坑边3 m时中主应力最大变化幅度为43%; 由图8(c)可知,距坑边8 m时中主应力最大变化幅度为31%;由图8(d)可知,距坑边12 m时中主应力最大变化幅度为2.8%,中主应力变化幅度随着基坑距离的增加逐渐减弱。由于基坑网格划分缘故,距离基坑越远处网格划分越大,因此,开挖3引起的拱效应范围为距坑边12 m。
综上所述,以应力增幅10%为判别值,将对应观测面处的中主应力影响范围标识于图7(b)—(d)中。在基坑逐步向下开挖过程中,由于表层土体性质较差,初始应力值小; 当基坑开挖深度不断增大,中主应力的变化幅度逐步减小。但是,在土层交界面处,由于不同地层侧压力系数不同,环向应力曲线存在突变段。在接近围护结构底部位置处,环向挤压效应不明显,也可说明现有围护结构嵌固深度已满足要求。
3.4 工况分析
3.4.1 基坑直径的影响
随着地下工程的规模越来越大,基坑直径逐渐变大。目前,最大的圆形基坑直径为70.6 m[10],本工程中基坑直径为22 m。为研究基坑直径对围护结构受力和变形规律的影响,本节选取基坑直径为22、33、44、55、66、77 m进行分析。不同基坑直径的桩体水平位移曲线如图9所示。由图可知: 当基坑直径分别为22、33、44、55、66、77 m时,围护结构最大水平位移为4.15、7.12、10.51、14.41、18.39、22.25 mm。通过上述分析可知,在同样的桩径和桩距情况下,随着基坑的直径增大,顶端变形约束效应减弱,变形增大,呈明显非线性。随着基坑直径的增加,产生的“拱效应”逐渐减弱。因此,在实际工程设计时应注意基坑直径对拱效应的影响。
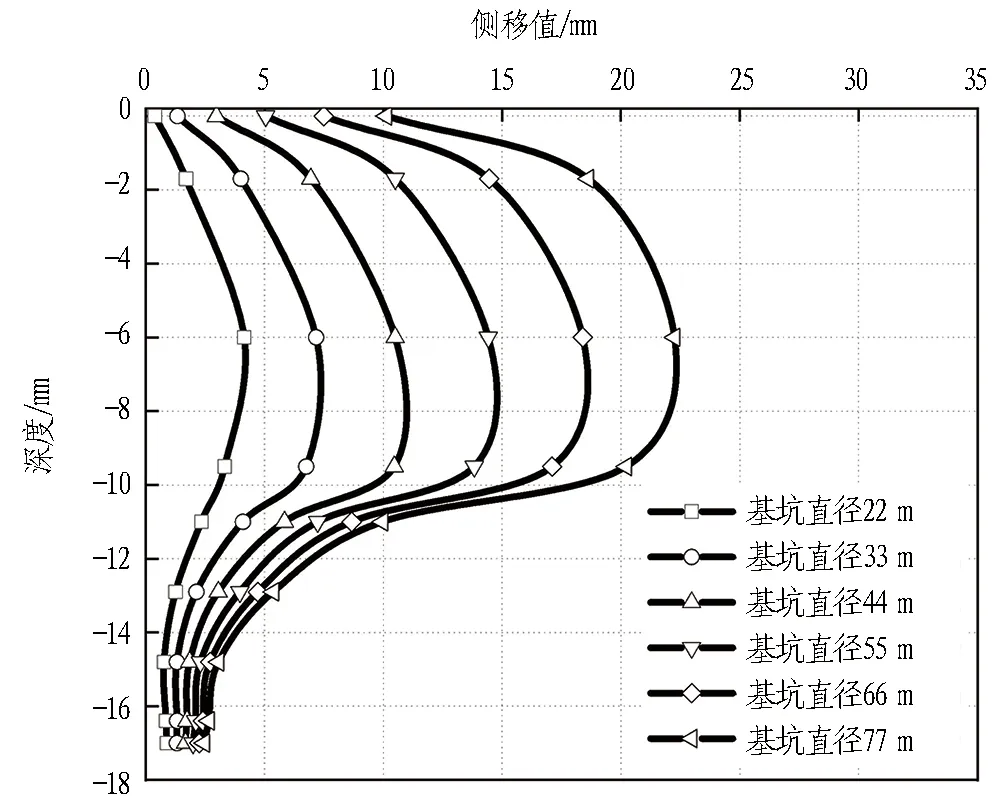
图9 不同基坑直径的桩体水平位移曲线图Fig. 9 Pile horizontal displacement curves of different foundation pit diameters
3.4.2 排桩直径的影响
本文中排桩直径为0.8 m,为研究筒排桩直径对围护结构受力和变形规律的影响,本节选取排桩直径为0.6、0.8、1.0 m进行分析。不同排桩直径的桩体水平位移曲线如图10所示。由图可知,当基坑直径为22 m、排桩直径为0.6、0.8、1.0 m时,围护结构最大水平位移为10.58、4.15、2.59 mm。其中,排桩直径为0.6 m时侧移值较大,而排桩直径为0.8 m和1.0 m时侧移值相差不大。因此,应综合考虑经济因素和变形控制要求选取基坑排桩直径。
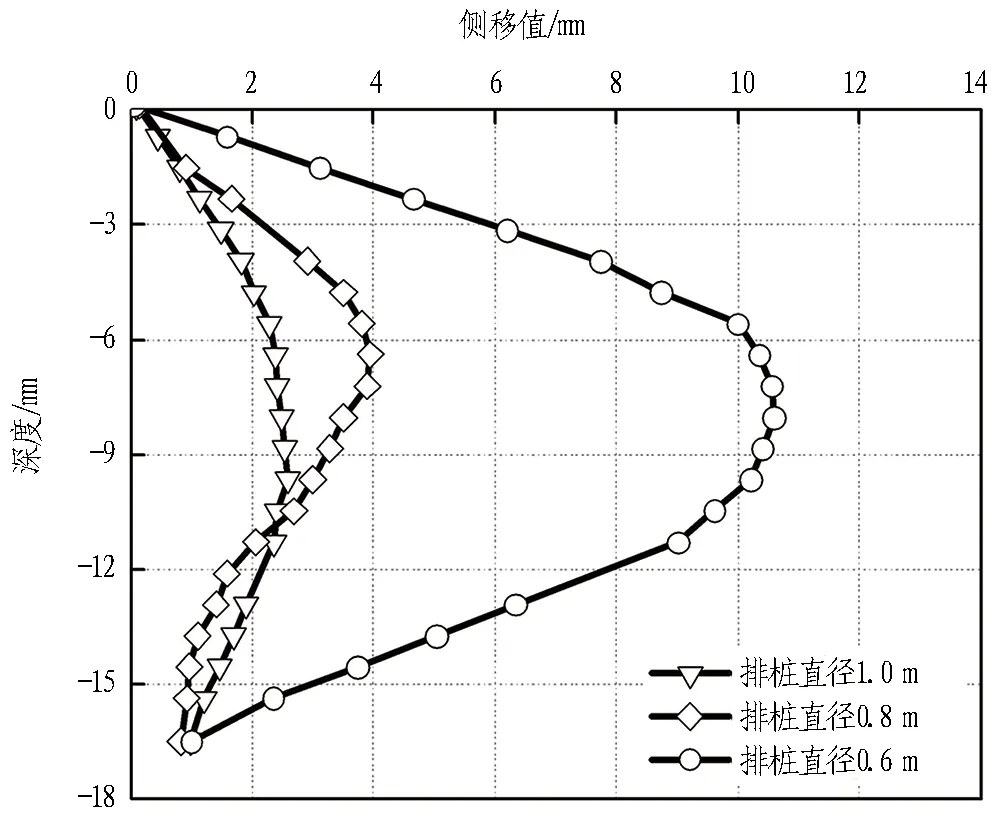
图10 不同排桩直径的桩体水平位移曲线图Fig. 10 Horizontal displacement curves of piles with different pile diameters
4 井筒基坑稳定性工况分析
为存放井筒式地下车库的大型机电设备,通常需要在原有基坑基础上进行土体的二次开挖,形成“坑中坑”,内坑土体的开挖势必会对基坑的稳定造成影响。为研究井筒式坑中坑的破坏失稳机制,基于强度折减法与有限元相结合的方法对基坑开展弹塑性分析[11]。
4.1 有限元强度折减法
强度折减法是通过不断折减土体的抗剪强度指标,将折减后的土体参数代入到有限元中进行试算,当计算结果与土体破坏准则一致时,此时的折减系数F称为最小安全系数。随着折减系数F的增加,土体的强度包线不断与莫尔圆靠近。当两者相切时,表明土体在安全系数F的条件下达到了极限平衡状态。
式中:τ为抗剪强度;c为黏聚力;φ为内摩擦角;F为强度折减系数;cm=C/F; tanφm=(tanφ)/F。
4.2 有无内坑工况的稳定性分析
不同折减系数下基坑塑性应变变化云图如图11所示。在图11(a)中,当土体抗剪强度参数不进行折减(F=1.0)时,桩底角部以及桩身外侧产生塑性区,且塑性区面积较小,基坑处于稳定状态;在图11(b)中,桩底及桩身外侧塑性区进一步扩大,桩身外侧的塑性区逐渐向基坑顶部发展;在图11(c)中,桩身外侧塑性区与坑中坑土体塑性区连通,逐渐形成弧形滑动带,此时折减系数F=2.0,随后继续折减,MIDAS/GTS会出现不收敛,同时剪切应变塑性区贯通[12],表明此时基坑处于失稳状态。

(a) F=1
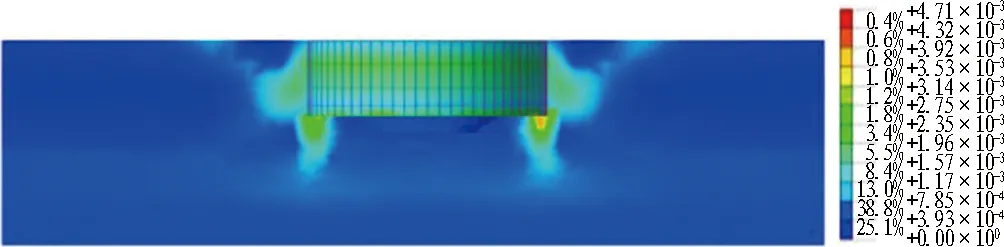
(b) F=1.4
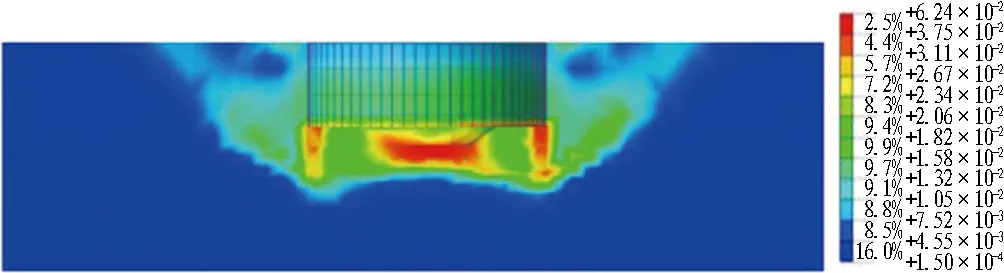
(c) F=2.0

(d) 无内坑F=2.3图11 不同强度折减系数下基坑塑性应变变化云图Fig. 11 Nephograms of plastic strain variation of foundation pit under different strength reduction coefficients
采用强度折减法对未进行土体二次开挖的基坑进行稳定性分析,由图11(d)得出最大折减系数F=2.3,此时云图显示塑性区与基坑底部贯通形成圆弧桩,且基坑底部塑性区域为向上凸起形式。通过与图11(c)对比可知,内坑的存在使得折减系数大小有着明显的区别,因此,在设计基坑内部存在二次开挖的情况时,需要考虑内坑对基坑整体的稳定性。
4.3 内坑不同开挖深度工况的稳定性分析
为研究内坑开挖深度h对基坑的影响规律,使基坑开挖深度、桩长和内坑上下表面内径保持不变,改变内坑开挖深度h对基坑塑性区发展情况进行分析,不对土体进行强度折减,即F=1。不同内坑开挖深度下的基坑塑性应变变化云图如图12所示。由图可知,随着内坑开挖深度的增加,使得被动区土体抗力损失,桩体嵌固端向坑内发生移动; 排桩刚度较大,基坑底部土体发生塑性变形。当内坑开挖4.8 m时,桩身外侧与内坑底部土体塑性区达到连通状态,容易产生基坑倾覆破坏。
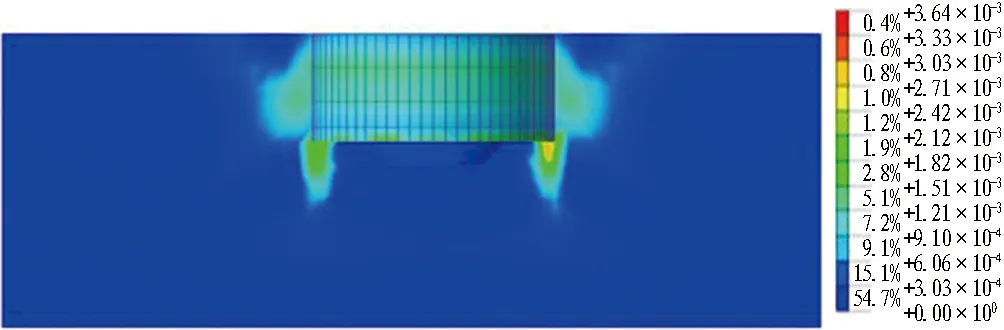
(a) h=2.4 m

(b) h=3.6 m

(c) h=4.8 m图12 不同内坑开挖深度下的基坑塑性应变变化云图Fig. 12 Nephograms of plastic strain variation of foundation pit under different excavation depth of inner pit
4.4 内坑不同平台宽度工况的稳定性分析
根据上述分析,内坑开挖深度h为3.6 m时土体进入塑性区发展阶段,此时坑中坑上平台宽度a为1.54 m。因此,在此开挖工况下改变上平台宽度a来分析基坑塑性发展情况。不同平台宽度下的基坑等效塑性应变云图如图13所示。由图可知,当坑中坑上平台宽度增加至2倍宽度时,桩底塑性区面积逐渐扩散,桩身外侧土体塑性区无变化。对于上下内径不同的内坑而言,由于内坑存在边坡,边坡下部的土体较为稳定,平台宽度的改变对于对桩体的影响较小。

(a) a=1.54 m
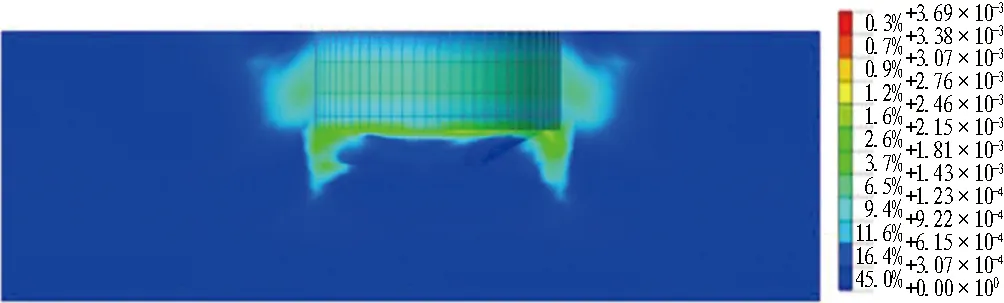
(b) a=3.08 m图13 不同平台宽度下的基坑等效塑性应变云图Fig. 13 Nephograms of equivalent plastic strain variation of foundation pit under different platform width
5 结论与建议
本文以哈尔滨省委广场井筒式智能停车场为工程背景,首先,根据监测数据对基坑的变形进行评述;其次,采用有限元软件MIDAS/GTS建立井筒基坑三维模型,探讨了井筒式基坑施工过程中的拱效应演变规律,并对基坑直径和围护桩桩径等主要影响参数进行分析;最后,基于强度折减法对基坑开展弹塑性分析,研究了二次开挖平台宽度和深度对基坑稳定性的影响。主要结论如下:
1)通过现场监测数据可知,井筒基坑由于空间“拱效应”的存在,桩体水平位移最大为3.5 mm,最大沉降量为11.6 mm。其中,随着基坑开挖深度的增加,“鼓肚”形状逐渐下移。
2)圆形基坑的环向拱效应,可以采用土体的中主应力矢量图进行表达。随着基坑开挖深度的逐步增大,其环向拱效应作用的土体范围也逐步扩大。
3)在对外坑支护结构进行计算时,需考虑内坑对外坑稳定性的影响。内外坑开挖深度之比为0.44时,需考虑内坑对基坑整体安全系数的影响。对于上下直径不同的内坑,由于内坑存在边坡,边坡下部的土体较为稳定,平台宽度的改变对桩体的影响较小。
通过有限元模拟和现场监测对井筒式基坑的变形及稳定性进行了分析,但有关冻胀效应对井筒式基坑的影响有待进一步深入研究。
——以淮南矿区为例

