无信号控制路段人行横道人车冲突风险分析

袁 黎，王曌亚，周荷媛

（1.河海大学，土木与交通学院，南京 210098；2.河海大学，计算机与信息学院，南京 210098）

0 引 言

无信号控制路段是未设置机动车和行人信号灯的路段。它是道路交通网的重要组成部分，其人行横道处因行人过街存在大量行人和机动车交织，是人车冲突的高发点。相较于信号控制路段，此处缺乏信号灯的保护和引导，行人和驾驶员存在着争夺路权的现象，极大地威胁着行人和驾驶员的人身安全。另外，与交叉口处的人行横道相比，机动车在路段人行横道处行驶速度较高，驾驶员警惕性不强。因此，衡量无信号控制路段人行横道处的安全水平并提出合理的人车冲突风险评估方法，对提升此位置行人通行安全水平极其重要。

近年来，国内外研究者对人车冲突进行了相关研究并取得了一定的成果，这些成果多为路段人车冲突概率、严重程度差别和评价。对于人车冲突概率，王俊骅等[1]基于交通冲突技术理论，通过摄影法获得车流量、路段平均车速和行人流量变量指标，证明了人车冲突服从负二项分布并建立人车冲突概率模型；陆斯文等[2]利用概率论方法，研究行人与机动车之间的交通冲突和碰撞微观机理，分别推导出人车冲突和碰撞概率微观模型。对于人车冲突严重程度。Hyden[3]通过冲突速度（CS）和冲突时间（TTC）来确定交通冲突严重度水平；李杰等[4]以TTC 为指标，将模糊推理思想引入交通冲突严重度判别，有利于实现自动冲突检测；牟瑞芳等[5]在Hyden 提出的指标基础之上，建立评价指标属性离散标准，构建人车冲突严重度矩阵，通过云模型理论实现评价指标定量计算与人车冲突严重度定性模糊概念的互相转换；除了CS 和TTC 两个指标之外，Almodfer 等[6]通过视频采集分析，研究了无信号控制路段各车道上的人车冲突分布情况，并以后侵入时间(PET)作为评估人车冲突的指标，提出一种基于车道的后侵入时间评估方法；Zhang 等[7]利用基于车道的后侵入时间（LPET）对多车道中段人行横道人车冲突进行分析。然而冲突严重性可能会伴随行人或驾驶员行为的变化而变化，上述指标作为严重性评估维度对此考虑不足，蒋沛[8]则采用行人安全边际时间（PSMT）作为PCS（Pedestrian-vehicle Conflict Severity）分级指标，对人车冲突分级，再根据分级后的结果构建基于Ordered probit 的人车冲突量化模型，对样本进行OP 回归分析后确定对无信号控制路段人车冲突严重程度有显著影响的因素；Kadali等[9]采用数据搜集的方法，评估了在印度无信号控制路段人行横道处人、车矛盾的严重程度，引入行人和驾驶员行为变化两个因素，并探讨其对严重程度的影响；Lu 等[10]以构建人车交互仿真模型，结合TTC的定义对行人安全进行评估。

上述研究大多只考虑时间和速度这两个冲突严重度指标，并且路段的安全评价结果都主要基于对单个机动车与个体行人之间冲突严重度的衡量，考虑冲突可能性和碰撞后果较少，不能很好地评价路段整体的人车冲突风险。而现有的冲突风险评估多集中在交叉口交通冲突上，袁黎等[11]提出“车流冲突线”概念，通过概率、严重度、冲突向后传递长度构建无信号交叉口安全风险评估；朱胜雪等[12]利用冲突指数、几何设计影响系数、安全设施影响系数建立交叉口安全评价指标；王春勤等[13]以交通冲突数与混合当量交通量的比值（TC/MPCU）作为指标对冲突进行分级评价；袁黎等[14]以期望值的观点构建交叉口车流当量冲突量，用以评估交叉口潜在风险性的高低。针对无信号路段的人车冲突风险评估较少。

除了严重度指标，对无信号控制路段人车冲突风险的考量也应该包括曝光程度和发生的概率[15]。此外，已有的冲突时间、后侵入时间等指标数据在实际中获取难度较高。故本文从车流-行人流出发，利用道路条件、交通流特征、数学概率与期望、物理碰撞原理、行人碰撞损伤等知识，探讨分析人车冲突概率、肇事后严重性以及期望人车冲突量，并给出具体量化方法。基于此，构建无信号控制路段人行横道处人车冲突风险评估模型，可在不需观测和统计冲突情况下，对无信号路段的安全性进行评估。该模型可为交通设计、管理者服务，让其快速得到目标无信号路段风险程度，为控制事故率、安全决策提供依据。

1 无信号控制路段人车冲突

1.1 无信号控制路段人车冲突定义

交通冲突指交通行为者在参与道路交通中，两个或两个以上的道路使用者在空间和时间上接近彼此到某种程度，此时如果二者的运动保持不变则会导致交通损害危险的发生。根据交通冲突定义及相关文献，本研究将无信号控制路段人车冲突定义为行人和驾驶员在参与道路交通中，双方感知到危险时，行人或驾驶员必须改变路线或速度或采取其他避险措施以避免碰撞的交通遭遇事件，如图1所示。

图1 人车冲突示意图Fig.1 Diagram of pedestrian-vehicle conflicts

1.2 无信号控制路段人车冲突特性

随机性、可避免性和严重性是人车冲突的三个基本特性。行人和机动车在一段时间内出现在路段的时间和位置是不确定的，故人车冲突是一件不可预测的高度随机事件，可用数学概率和期望知识来描述人车冲突的随机性。行人和机动车在不断接近的过程中，行人和驾驶员出于求生本能会采取一定的避险行为来规避冲突，因此人车冲突具有一定的可避免性。

当人车冲突发生时，因冲突发生的后果接近肇事事故的程度各异而存在不同的严重性。根据严重程度不同可将人车冲突分为无冲突、一般冲突和严重冲突三种，其中严重冲突是最接近事故的冲突。

2 无信号控制路段人车冲突风险评估模型构建

在分析无信号控制路段人车冲突特性的基础上，本研究采用人车冲突概率、人车冲突肇事后严重性、人车冲突期望冲突量三个指标来构建无信号控制路段人车冲突风险评估模型。模型如下式所示：

式中：Ai为人车冲突风险值；Pi为人车冲突概率；Ti为人车冲突严重程度；Di为人车冲突期望冲突量；i为与行人发生冲突的机动车类型。

无信号控制路段人车冲突风险评估流程如图2所示。

图2 人车冲突风险评估流程Fig.2 Establishing process of risk evaluation model

根据《城市道路工程设计规范》（CJJ37—2012），本研究将机动车分为小客车和大型车，i=1,2 分别代表小客车和大型车（“小型普通客车”和“轻型普通货车”统一简称为“小客车”，“大型普通客车”和“重型普通货车”统一简称为“大型车”）。考虑到在城市道路上行驶的小客车多为小轿车，大型车多为公交车或大型巴士，综合考虑载客因素并参考《机动车运行安全技术条件》（GB7258—2017）和《汽车、挂车及汽车列车外廓尺寸、轴荷及质量极限》（GB1589—2016），确定出小客车和大型车的相关基本参数假定值，如表1所示。

表1 不同车型的基本参数Tab.1 Essential parameters of different vehicle models

2.1 人车冲突概率模型

无信号控制路段人行横道处发生人车冲突时，行人和机动车将同时出现在过街人行横道某处，故针对无信号控制路段的单一车道，分析机动车和行人出现在人行横道处的概率。

2.1.1 机动车出现在人行横道处概率

研究显示机动车到达服从泊松分布，则机动车在行人穿越机动车宽度范围所需时间内到达的概率可用下式表示：

式中：PVi为i种机动车到达行人行横道的概率；QVi为i种机动车流量（pcu/h）；Ei为i种机动车宽度（m）；VP为行人的步行速度（m/s）。

2.1.2 行人出现在人行横道处概率

行人在无信号控制路段人行横道处过街时的过街行为包括两个部分：一是行人到达人行横道过街起点；二是行人选择合适过街间隙选择过街。因此分析行人出现在人行横道处概率时需要考虑上述两部分的概率。

（1）行人到达概率

研究显示行人到达与机动车到达一样服从泊松分布，则行人在机动车穿越行人位置所需时间内到达的概率可用下式表示：

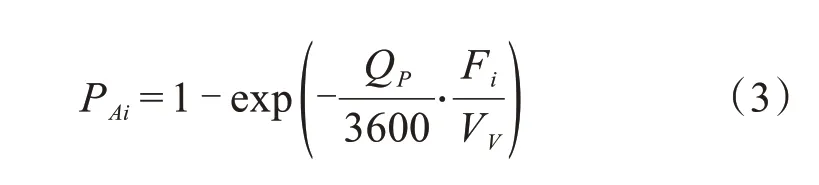
式中：PAi为行人在i种机动车穿越行人位置所需时间内到达的概率；QP为行人流量（人/h）；Fi为i种机动车长度（m）；VV为机动车速度（m/s）。

（2）行人选择过街概率

假设道路宽度为L，当行人能顺利穿越道路时，车头时距需大于所设置最小可接受安全间隙t0=L VP，即在t0时间内没有机动车到达，此时行人选择过街。由于机动车到达服从泊松分布，车头时距则服从负指数分布，行人选择过街概率可用下式表示：式中：Pi为人车冲突概率值；H为路段道路车道数。

2.2 人车冲突肇事后严重性分析

在行人与车辆发生碰撞时，碰撞时的能量会造成行人、驾驶员的受伤或者死亡以及车辆的变形，碰撞时产生的能量即机动车与行人之间传递的动能的大小与事故的严重性呈正相关。此外，根据文献[16]中关于人车碰撞数据研究，可总结得到影响行人损伤严重程度的主要因素是碰撞速度和车辆体型。其中随着碰撞速度的增加，行人受重伤的概率增大；同时与小型车相比，行人在被大型车撞击时受重伤的风险更大。因此本研究分车型探讨人车冲突肇事后的严重性，依据物理动力学原理并利用机动车的质量以及碰撞速度来量化严重程度。

（1）不同车型的人车冲突严重程度

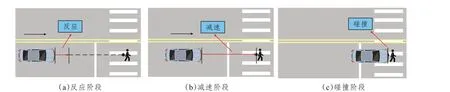
图3 人车碰撞示意图Fig.3 Diagram of pedestrian-vehicle collisions

依据物理动力学以及数学概率知识可得到人车冲突的严重程度如下式所示：

式中：Ti为i种机动车冲突严重程度；λ为双向所有车种车流量之和（pcu/s）；tP为驾驶员的反应时间（s），依据《城市道路设计手册》推荐混合车流取1.5 s；tsi为i种机动车减速至完全停止所需时间（s）；ai为i种机动车的制动减速度（m/s2）；VV为机动车的行驶速度（m/s）；Mi为i种机动车的质量（t）。

同时，碰撞位置的不同也会影响人车冲突肇事后的严重性。因碰撞过程中的动力学响应非常复杂，行人头部损伤与胸部损伤之间具有较强的相关性[17]，故本文仅以行人的头部损伤指标HIC（Head Injury Criterion）作为判别不同碰撞位置对人车冲突肇事后严重性造成的影响。从计算公式看，HIC 是对行人头部响应加速度短时间内的积分，且指数为2.5[18]。因此，为简化计算，可以不同碰撞位置下行人抛出速度比的2.5 次方作为标准探讨不同碰撞位置所带来的影响。

行人与机动车前部碰撞位置是随机的，假设碰撞位置服从均匀分布[18]，则碰撞位置在机动车的左侧、中部、右侧（各部分宽度为车宽的三分之一）的概率是一致的。在人车碰撞过程中，行人侧向形态被机动车碰撞的情况占比为68 %[18]，加之人行横道上行人纵向穿越过街，故本文主要考虑行人侧向形态的碰撞。

根据文献[19]中关于行人抛距与机动车碰撞速度之间关系的研究，可分别得到行人侧向形态与机动车侧边三分之一、中部碰撞时行人抛距与机动车碰撞速度的拟合关系，并结合行人抛距公式，得到行人抛出速度比，如式（10）、（11）所示：

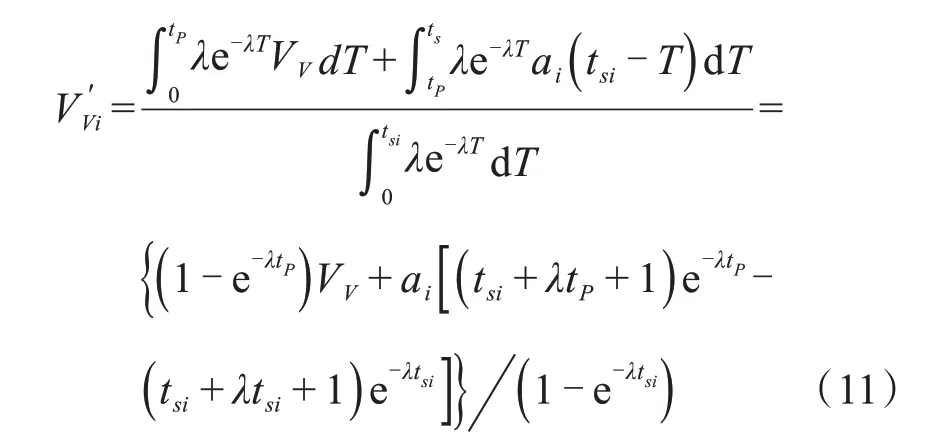
式中：ei为行人与i种机动车在不同位置碰撞时的抛出速度比；vai为行人侧向形态与i种机动车侧边三分之一碰撞时抛出速度（m/s）；vbi为行人侧向形态与i种机动车中部碰撞时抛出速度（m/s）；hi为与i种机动车碰撞后行人平抛高度（s），行人被平抛的高度大致是机动车发动机罩高度与行人躯体半径之和[19]，本文取机动车高度的一半；φ为行人与地面的摩擦系数，本文取0.48[19]；V′Vi为i种机动车的碰撞速度（m/s）。

（2）权重一致化

为避免扭曲期望人车冲突量的计算，需保持两种车型的冲突权重值的总和为2，权重值计算结果如表2所示。

表2 各车型期望人车冲突严重比权重值一致化Tab.2 Weight value of the expected pedestrian-vehicle conflict of each vehicle model

2.3 期望人车冲突量

由于人车冲突发生时行人的步行方向与机动车的行进方向相互垂直，且行人需要从人行横道的一侧行至另一侧，则行人与机动车可能会产生交叉冲突。假设每股行人流对应行人数为S，每股机动车流对应当量交通量为N（其中小客车为N1，大型车为N2，N=N1+N2）。当发生人车冲突时，S个行人对应于S+ 1 个行人位置中，任意一个位置都有可能和N辆机动车交叉冲突，则根据排列组合可知S个行人与N辆机动车发生冲突的可能数F以及概率Pc：

2.4 模型构建

根据上述关于人车冲突概率、冲突严重性、期望冲突量的分析，构建无信号控制路段人行横道处人车冲突风险评估模型，即式（1）可改写如下：

2.5 安全风险等级划分

以人车冲突风险值A为划分指标，将路段危险程度划分为很安全（A 级）、较安全（B 级）、一般（C级）、较危险（D 级）、很危险（E 级）这5 个安全风险等级，安全风险等级越高，事故发生的概率越大[20]。在江苏省南京市15个无信号控制路段进行现场观测，并以问卷调查的方式问询得到受访人员的主观危险度感受。梳理调查问卷结果，结合模糊理论得到人车冲突风险值与不同安全风险等级之间的隶属函数值，利用Origin软件对不同等级下的隶属函数值进行拟合[21]。由于拟合输出结果较多，故以参数少、相关性高为筛选原则对拟合结果进行筛选。筛选后的拟合结果如图4所示。

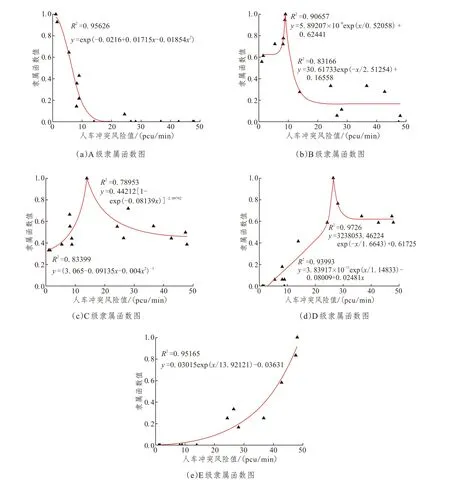
图4 各安全风险等级隶属度拟合曲线Fig.4 Fitting curve of membership degree of each risk level

为了将隶属函数描述的迷糊集合明确化，需要通过水平截集α确定新的集合。水平截集α越高，则对安全风险等级的描述越苛刻。为了更为保守且高标准地划分安全风险等级，本文选用α=0.9 时各等级下隶属度大于或等于α的人车冲突风险值集合作为等级区间，并以区间右边界值与相邻等级的左边界值的平均值作为最终区间划分标准值，具体各等级区间左右边界值以及划分情况如表3、表4所示。

表3 无信号控制路段各安全风险等级区间边界值（α=0.9）Tab.3 Interval boundary value of each risk level at unsignalized mid-block crosswalks（α = 0.9）

表4 无信号控制路段安全风险等级划分Tab.4 Risk level of unsignalized mid-block crosswalks

2.6 模型有效性验证

为了验证无信号控制路段人车冲突风险评估模型的合理性，选择南京市15 处无信号控制路段作为数据采集的对象，计算出模型结果。同时，组织8 名交通从业人员依据对现场录像的观察以及自己的知识和经验，对这15 处路段的人车冲突风险性打分（100 分制），分数越低，路段人车冲突风险性越高。利用SPSS 软件对模型计算值与主观打分均值进行相关性分析，如表5和图5所示。

表5 模型计算值与主观打分均值相关性分析Tab.5 Relativity analysis of the values calculated by the model and subjective average score

图5 模型计算值与主观打分均值相关性分析Fig.5 Relativity analysis of the values calculated by the model and subjective average score

由表5 和图5 可知，无信号控制路段人车冲突风险评估模型计算值与主观打分均值之间呈较强的负相关性，模型具有一定的合理性。

3 实例应用

以南京市一处无信号控制双向4车道路段（南京古南都饭店）为例进行实证研究，此处道路限速50 km/h，宽度为12 m，人行横道宽度为4.9 m，其地理位置如图6（a）所示。

图6 南京古南都饭店实地调查情况Fig.6 Survey in Nanjing Grand Hotel

3.1 数据获取

选择摄影法，在平峰时段（15:00 开始计时）对此处无信号控制路段进行为期1 h 的观测。利用图林白板和视频播放软件获取并处理数据（如图6（b）所示），得到行人流量、车流量、行人步行速度以及车辆速度等数据的观测值，如表6所示。

表6 模型参数标定值Tab.6 Model parameters calibration

3.2 人车冲突风险值计算

（1）人车冲突概率

根据式（6）计算不同机动车类型下的冲突时间间隔，同时接受路段人行横道人车冲突概率等于1 减去路段人行横道内每条车道均不发生冲突的概率，即结合式（7）、（8）计算得到路段行人与小型车、大型车冲突概率分别为P1=0.000 536,P2=0.000 06。

（2）肇事后严重性分析

肇事后严重性分析可根据式（9）计算得出T1=100.3678,T2=1075.883，再根据式（10）、（11）计算得出e1=1.0126,e2=1.0123。故各车型期望人车冲突量权重值一致化结果如表7所示。

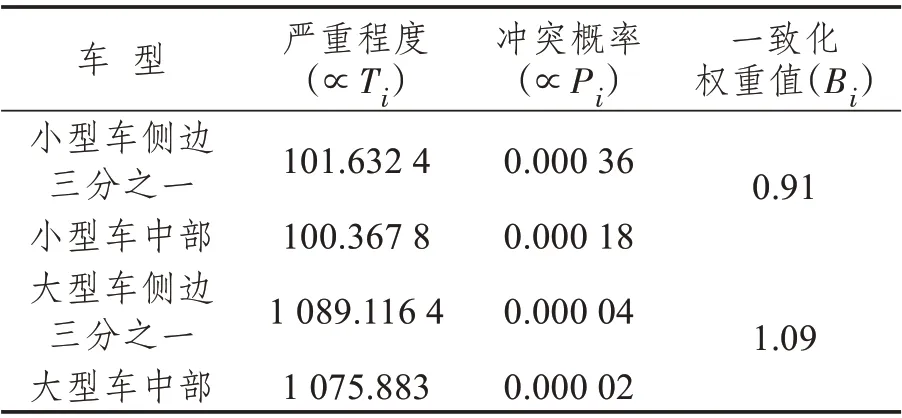
表7 各车型期望人车冲突量权重值一致化Tab.7 Calculation of the weight value of the expected pedestrian-vehicle conflict of each model

（3）期望人车冲突量

根据式（15）计算得到每分钟内人与小型车、大型车的期望人车冲突量D1=9.54pcu/min,D2=0.25pcu/min。

（4）人车冲突风险值

根据式（16）计算得到无信号控制路段人行横道处人车冲突风险值为：

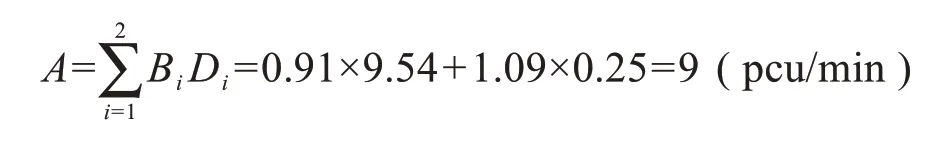
结合表4 无信号控制路段安全风险等级划分标准，判断该无信号控制路段人行横道处人车冲突风险等级为B级，处于较安全水平。

4 结 论

在分析无信号控制路段人行横道人车冲突基本特性的基础上，构建无信号控制路段人行横道人车冲突风险评估模型，划分安全风险等级并进行实例应用。

（1）分析无信号控制路段人车冲突基本特性。经剖析无信号控制路段人行横道处行人与机动车在发生冲突时的过程，得出无信号控制路段人车冲突的基本特性：随机性、可避免性及严重性。

（2）构建无信号控制路段人车冲突风险评估模型。不同于仅从速度和时间的角度来考虑单个机动车与个体行人之间冲突的严重程度，本文模型综合考虑了人、车、路的相关基本参数以及人车冲突的概率、肇事后的严重性和期望冲突量这三个指标，其中还将行人与机动车在不同碰撞位置下对严重性所带来的影响纳入探究范围，更为全面地描述人车冲突的可能性、严重性和曝光程度。该模型可以针对某一具体无信号控制路段人行横道处的人车冲突风险进行评估。将调查数据带入模型中获得模型计算值，其与交通从业人员主观打分均值之间的相关性分析验证了模型的有效性。

（3）建立无信号路段人车冲突安全风险等级划分标准。基于受访行人对无信号路段危险感受度调查问卷，利用模糊隶属函数的分级方法得到在水平截集为0.9条件下的5个风险等级的区间边界值，最后确定出无信号控制路段人车冲突安全风险值的等级标准量化值。