面向站内换乘便捷性的到发线运用优化研究

胡留洋，鲁工圆，詹丛茵，侯 倩，彭 慧

（1.西南交通大学，交通运输与物流学院，成都 611756；2.综合交通运输智能化国家地方联合工程实验室，成都 611756）

0 引 言

截至2021 年底，我国高速铁路运营里程超4万km，高速铁路网络日趋复杂，客流量日益增加。我国高速铁路采用跨线列车直达为主的运输组织模式，这种模式存在区域客流需求不能满足，列车运行图结构变动频繁，路网通达度低等问题[1]，通过在车站内组织旅客中转换乘，可在一定程度上解决以上问题，如何在大型高铁站组织旅客中转换乘值得深入研究。大型高铁站是高速铁路网络上旅客中转换乘的重要节点，往往衔接多条高铁线路并配备动车段，具有到发线和站台数量多、站内列车作业种类多样、列车进路及接续关系错综复杂的特点[2]。由于大型高铁站的这些特点，以及在编制到发线运用方案时未充分考虑旅客中转换乘问题，旅客往往无法在站内方便快捷地换乘。表1为“12306 手机App”推荐给旅客，由漯河西经郑州东至成都东，换乘接续时间低于25 min的方案。由表1 可知，除去开车前停止检票时间5 min，旅客要在11～20 min 内跨越19～26 个站台完成换乘，反映了旅客在大型高铁站内换乘不便捷的问题。

表1“12306手机App”推荐部分换乘方案Tab.1 Recommended transfer schemes from the“12306 mobile App”

通过调整列车图定到发线的方式，可在一定程度上解决大型高铁站内旅客换乘不便捷的问题。如：将G258 次列车的图定4 号到发线调整为16 号到发线，G89 次列车的图定30 号到发线调整为21 号到发线，旅客只需在17 min 内从16 号站台走行至21号站台，距离大幅缩短。基于此，本文研究如何通过优化到发线运用方案，提升旅客在大型高铁站内换乘的便捷性。

面向站内换乘便捷性的到发线运用优化研究需要满足以下3方面要求：

（1）站内换乘便捷性要求

到发线运用优化方案应保证换乘接续列车停靠在距离合适的两条到发线上，使旅客能在有限时间内便捷换乘。

（2）可操作性要求

到发线运用优化方案应在满足到发线固定使用方案前提下，尽可能少改变到发线运用图定方案。

（3）安全性要求

到发线运用优化方案应满足列车占用到发线安全间隔时间以及列车占用接发车进路、到发线不冲突原则。

国内外学者针对到发时刻固定的到发线运用优化问题进行了大量研究。文献[3]将问题转化为加权节点打包问题，以最大化列车径路选择偏好为目标，基于预处理、有效不等式和分支定界算法设计算法求解。文献[4]将“时间片”的概念引入到发线运用优化问题，简化了到发线占用相容性约束，设计最小最大蚂蚁系统算法求解。文献[5]以旅客列车的接发车作业进路为决策，以道岔和到发线占用相容性为约束，以最大化接发车作业进路效用和到发线运用效用为目标，设计基于极大列车过站径路方案的k剔除邻域系的模拟退火算法进行求解。文献[2]将到发线运用调整问题分解为到发线运用方案编制子问题与列车到发时刻调整子问题，以列车运行晚点和车站作业秩序影响双方面最小化为目标，设计基于分支定界的算法框架对到发线运用方案编制子问题进行求解。文献[6]以到发线固定使用、到发线均衡使用、旅客服务质量为目标建立多目标0-1 规划模型，通过功效系数法统一目标函数量纲，转化为单目标，利用分支定界算法求解。文献[7]考虑轨道电路分段解锁的特性，结合列车作业链思想，以提高到发线运用时空均衡性和车站作业计划稳定性为目标，建立列车进路链式分配模型，设计贪婪模拟退火算法求解。

对旅客站内换乘的研究多从换乘客流量和换乘等待时间角度评价旅客站内换乘的质量。文献[8]研究单个大型换乘站旅客列车换乘接续方案优化，以最大化有效接续客流量、最小化旅客在站无效等待时间为目标，分别建立列车接续关系已定、未定模型，并对模型进行求解。文献[9]明确高铁枢纽站列车接续优化是优化换乘接续列车到发时刻，以最大化换乘客流量和最小化换乘等待时间为目标，建立列车换乘接续优化模型，并设计遗传算法进行求解。文献[10]分析高铁枢纽站旅客换乘过程，提出中长途客流换乘满意度概念，以平均换乘满意度和枢纽车站列车到发均衡性为优化目标，建立基于列车接续优化模型，并设计改进遗传算法进行求解。

亦有学者将旅客站内换乘纳入到发线运用优化研究。文献[11]考虑咽喉区进路，对客运专线与既有线衔接站的到发线运用进行优化，以列车满足同台换乘的客流量最大化作为目标之一，设计遗传算法求解。文献[12]基于咽喉区进路与到发线一体化优化，以最大化同站台换乘满足的潜在客流量为目标之一，设计遗传算法进行求解。文献[13]对高速铁路车站咽喉区进路与到发线进行综合优化，考虑接续列车同台换乘，设计多目标遗传算法求解。

综上，既有研究存在以下问题：

（1）考虑换乘的到发线运用优化研究中：①换乘往往只是优化目标之一且不是主要目标，或者只在约束中考虑换乘而不将其作为目标；②将旅客站内换乘局限于同台换乘，不符合大型高铁站到发线和站台数量多，到发线固定使用，难以实现同台换乘的实际情况；③多以潜在换乘客流作为目标，忽略了大量存在换乘接续关系的列车对，且在客流发生变化时，需要重新制定到发线运用方案，造成资源浪费。

（2）对旅客站内换乘的研究：单从换乘客流和换乘等待时间评价旅客站内换乘质量，忽略了走行距离对旅客站内换乘便捷性的影响。

针对以上问题，本文根据能实现换乘接续的列车对的到发时间间隔和停靠到发线距离，将其划分为3种列车对，并相应描述旅客在大型高铁站站内的3 种换乘方式。通过到发线运用优化的手段，增加站内可供旅客选择的满足列车种类、方向、到发时间间隔、停靠到发线距离等条件的换乘接续列车对的数量，从而达到提升旅客站内换乘便捷性的目的。

1 问题描述与假设

1.1 问题描述

面向站内换乘便捷性的到发线运用优化研究，是指通过优化到发线运用图定方案，提高旅客站内换乘便捷性，如引言部分提到的郑州东站旅客换乘实例。具体解释如下：在给定车站站型、到发线固定使用方案、列车时刻表的前提下，改变部分列车的图定到发线，增加车站可供旅客选择的换乘接续列车对数，并满足列车图定到发线数量改变上限，一列车只能占用一条过站径路，列车过站径路不存在时空冲突等要求。

换乘列车指有换乘需求的旅客完成前段旅程在换乘站换出的列车；接续列车指有换乘需求的旅客完成后段旅程需要换入的列车[14]。换乘接续列车对指换乘列车和接续列车组成的列车组合。旅客站内换乘，指有换乘需求的旅客自换乘列车停靠站台面，不出站经由站内换乘路径前往接续列车停靠站台面。需要注意的是岛式站台具有两个站台面，侧式站台只有一个站台面。旅客站内换乘便捷性要求旅客在站内能方便、快捷地完成换乘。“方便”要求站内可供旅客选择的换乘接续列车对数量多、换乘接续关系丰富；“快捷”要求站内可供旅客选择的换乘接续列车对停靠两个站台面邻接的到发线间距合适、到发时间间隔合理。站内换乘总体上分为站厅换乘和站台换乘两种方式。站台换乘中的同站台换乘又可分为同台同面换乘、同台异面换乘[15]。本文考虑旅客在大型高铁站站内换乘的3种方式：同台同面换乘、同台异面换乘、短距离站厅换乘，如图1所示。

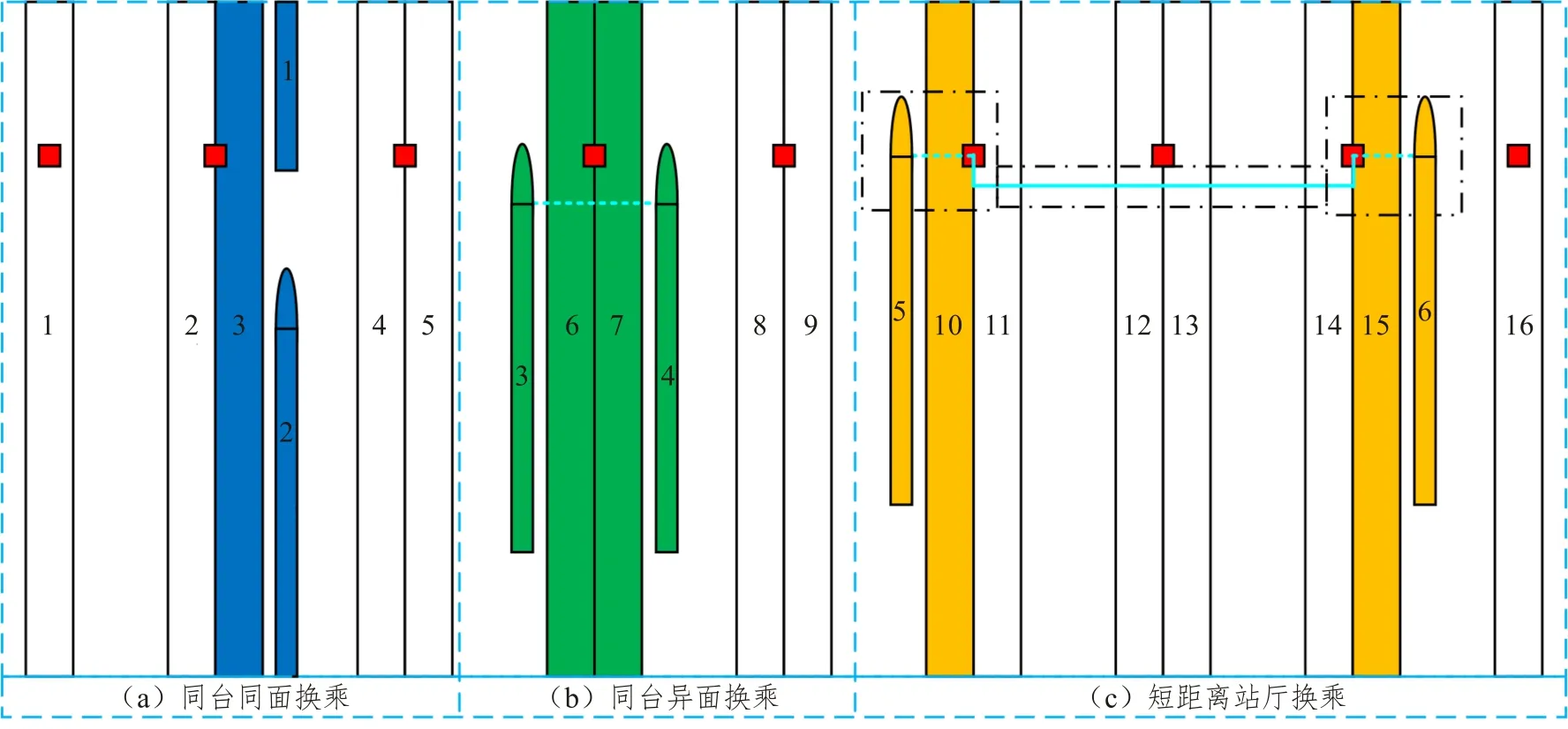
图1 大型高铁站旅客站内换乘方式示意图Fig.1 Schematic of passenger transfer modes at a large high-speed railway station

（1）同台同面换乘

同台同面换乘方式指旅客通过先后占用同一到发线的两列列车进行换乘，如图1(a)中列车1、2先后占用站台面3侧到发线。

（2）同台异面换乘

同台异面换乘方式指旅客通过占用岛式站台两侧到发线的两列列车进行换乘，如图1(b)中列车3、4占用站台面6、7侧到发线。

（3）短距离站厅换乘

短距离站厅换乘方式指旅客经由便捷换乘电梯、站厅，通过占用两个相距一定距离的站台面侧到发线的两列列车进行换乘。两站台面距离应能保证旅客在合理时间内便捷换乘，如图1(c)中列车5、6占用站台面10、15侧到发线。

考虑大型高铁站到发线数量多且固定使用、站台数量多的实际情况，以上3 种换乘方式中，同台同面换乘最难实现，同台异面换乘次之，短距离站厅换乘最易。但从提高旅客换乘便捷性的角度，同台同面换乘最为便捷，同台异面换乘稍次之，短距离站厅换乘最不便捷。将以上3种换乘方式纳入目标函数，要综合考虑大型高铁站实际情况和旅客换乘便捷性，合理设置目标函数各部分权重系数。

面向站内换乘便捷性的到发线运用优化研究要满足特定约束，包括列车占用过站径路唯一性约束，列车占用过站径路相容性约束以及到发线运用图定方案改变限度约束。列车的过站径路由列车接车进路、到发线和发车进路拼接而成，接发车进路唯一确定列车占用的到发线[5]。列车占用过站径路唯一性约束指一列列车只能选择一条过站径路。列车占用过站径路相容性约束指任意两列列车的过站径路在时间、空间上不存在冲突。在此引入到发线运用图定方案改变程度与改变限度。到发线运用图定方案改变程度指到发线运用优化方案相较于图定方案到发线改变（改变后仍符合到发线固定使用方案）的列车数量占列车总数的比例。到发线运用图定方案改变限度是到发线运用图定方案改变程度的上限，取值0%～100%。到发线运用图定方案改变限度约束指到发线改变的列车数量存在上限。

在给定车站站型图与到发线固定使用方案的前提下，可根据列车的接入发出方向、可占用的接发车进路及到发线，预先生成任意列车的可行过站径路集。考虑换乘接续条件，从列车的可行过站径路集中可预先筛选出满足3 种换乘方式的换乘接续列车及过站径路的两两组合。如图2所示，若占用过站径路1=（①，1，⑤）的列车1 与占用过站径路2=（②，2，⑥）的列车2 满足旅客进行同台异面换乘的条件，则将其记为（（1，1），（2，2）），并将其称为同台异面换乘接续列车径路对，由此可生成3种换乘方式的换乘接续列车径路对集。

综上，面向站内换乘便捷性的到发线运用优化研究的实质是从列车的可行过站径路集中筛选出符合特定约束的列车径路，并最大化其中满足3种换乘方式的换乘接续列车对数（根据过站径路占用唯一性约束，换乘接续列车径路对数即换乘接续列车对数）。

1.2 问题假设

为便于后续阐述，根据国内大型高铁站作业秩序，提出以下假设：

（1）车站站型已知。

（2）列车到达和出发时刻、列车各接发车进路走行时间、进路办理时间、列车到发线走行时间已知。

（3）不考虑立即折返列车中的转线立折列车[12]。

（4）在判断列车过站径路冲突时，将共用车底、只占用接车进路的折返前列车与只占用发车进路的折返后列车视为1 列占用1 条过站径路的停站列车；将折返前列车的序号作为此停站列车的序号。此停站列车的到达时刻即为折返前列车的终到时刻，出发时刻即为折返后列车的始发时刻。在统计换乘接续列车径路对时，将折返前后两列车视为占用同一条过站径路的终到、始发列车共两列列车。在车站不转线，进行终到、始发作业的同一交路上、共用车底的前后两列列车也照此处理。

（5）车站内，交路始端的始发列车从车站配备动车运用所出发，到达车站的时刻为其始发时刻往前推20 min；交路末端的终到列车去往车站配备动车运用所，出发时刻为其终到时刻往后推20 min。

（6）站台容量可保证旅客换乘不受限制。

2 模型构建

2.1 备选集生成

根据1.1 列车可行过站径路集、换乘接续列车径路对集的定义，2.1.1 提前生成所有列车的可行过站径路集。2.1.2 基于生成的列车可行过站径路集，筛选符合3 种换乘方式的换乘接续列车径路对集。

2.1.1 可行过站径路集生成

图2 为某小型高铁站站场图。该小型高铁站衔接A、B 两个方向，有4 条到发线，8 条咽喉区进路。到发线固定使用，1、2 到发线接发A 至B 方向列车，5、6 到发线接发B 至A 方向列车。令P为所有列车的可行过站径路集合，p为可行过站径路，p∈P。若列车G1 从A 方向进站，B 方向出站，则列车G1 的可行过站径路有p1=(①,1,⑤)，p2=(②,2,⑥)。列车G1 的可行过站径路集为PG1=(p1,p2)，PG1⊂P。

图2 某小型高铁站站场图Fig.2 Station yard of a small high-speed railway station

令K为列车集合，k= 1,2,…,kmax为列车索引，k∈K。任意列车k的可行过站径路集为Pk⊂P。在车站立即折返或进行终到、始发作业的同一交路上、共用车底的前后两列列车，集合K只包含前车的索引，集合K+是与前车对应的后车索引集合。在判断列车过站径路冲突时k∈K，在统计换乘接续列车径路对时k∈K∪K+。

2.1.2 换乘接续列车径路对集生成

若列车k1、k2∈K∪K+，k1≠k2为一对换乘接续列车 对，p1、p2分 别 为k1、k2占 用 过 站 径 路，则((k1,p1),(k2,p2))换乘接续列车径路对需要满足：

（1）换乘接续列车对种类条件：换乘接续列车对是形如终到列车→出发列车、终到列车→停站列车、停站列车→停站列车、停站列车→出发列车的列车对。

（2）换乘接续列车对接入发出方向条件：①当换乘列车为终到列车，接续列车为始发列车或停站列车时，换乘列车的接入方向与接续列车的发出方向不相同，即ok1≠dk2。②当换乘列车为停站列车，接续列车为始发列车或停站列车时，换乘列车的接入方向与接续列车的发出方向不相同，同时换乘列车的发出方向与接续列车的发出方向也不相同，即ok1≠dk2且dk1≠dk2。

按照以上方法构建换乘接续列车径路对集，首先确定换乘接续列车对接入发出方向，可最大限度保证存在换乘客流的换乘接续列车对被选择；其次将同台同面、同台异面换乘接续列车对的到发时间间隔控制在5～15 min，保证旅客换乘安全，也保证站台上不滞留过多旅客（因开车前提前15 min 检票、提前5 min 停止检票）；最后按照时间段对短距离站厅换乘进行细分，保证旅客的换乘时间与换乘走行距离更加匹配。

综上，可生成同台同面换乘接续列车径路对集SP，同台异面换乘接续列车径路对集DP，短距离站厅换乘接续列车径路对集SHϕ，ϕ= 1,2,…,6。ϕ对应表2 短距离站厅换乘接续列车径路对的6 种细分类型（ϕ= 1,2,…,6 分别对应到发时间间隔为15～20 min、20～25 min、25～30 min、30～35 min、35～40 min、40～45 min）。

表2 换乘接续列车对到发时间间隔及停靠到发线距离条件Tab.2 Arrival-departure time intervals and platform distance conditions of transfer-connection train pairs

2.2 目标函数

2.2.1 目标函数权重设置

根据1.1 问题描述，面向站内换乘便捷性的到发线运用优化研究的目标为最大化分属于3 种换乘方式的换乘接续列车对数。令α为同台同面换乘方式的权重；β为同台异面换乘方式的权重；η为短距离站厅换乘方式的权重。3 种换乘方式的权重需综合考虑大型高铁站实际情况与旅客换乘便捷性，合理设置。

2.3 约束条件

2.3.1 列车占用过站径路各时段、时刻关系约束

图3、图4为列车k∈K从接车进路开始办理时起至尾部出清发车进路时止，占用过站径路p的示意图。图3 为非通过列车的示意图，图4 为通过列车的示意图。

图3 非通过列车占用过站径路示意图Fig.3 Schematic of a stop train occupying a station-passing path

图4 通过列车占用过站径路示意图Fig.4 Schematic of a non-stop train occupying a station-passing path

为方便建模，将通过列车的过站径路视为由接车进路、到发线、发车进路拼接而成。接发车进路走行时间、到发线走行时间按照列车不停站计算。通过列车的到发时刻为同一时刻，由接入发出时刻、进路走行时间、到发线走行时间推算。

（1）车长m：动车组列车的长度。

（2）接车进路r：列车k进站经过的，从咽喉区与接入方向A 衔接的轨道区段至与到发线b衔接的轨道区段间的咽喉区进路（具有方向性，A→b）。

（3）发车进路l：列车k出站经过的，从咽喉区与到发线b衔接的轨道区段至与发出方向B 衔接的轨道区段间的咽喉区进路（具有方向性，b→B）。

（4）过站径路p：列车k的过站径路p由接车进路r，到发线b，发车进路l组成。

（5）进路办理时间σl：接发车进路办理时间。

（6）列车到发线走行时间σc：对于非通过列车，自列车k尾部出清接车进路时起至该列车在到发线上停稳时止的时间，或自列车k从到发线上启动时起至该列车头部开始占用发车进路时止的时间。对于通过列车，自列车k尾部出清接车进路时起至该列车头部抵达停车位置标时止的时间，或自列车k头部抵达停车位置标时起至该列车头部开始占用发车进路时止的时间（停车位置标作为标志点，列车并不停车）。

（7）接车进路走行时间trp：自列车k开始占用过站径路p∈Pk的接车进路r时起至该列车尾部出清接车进路时止的时间。

（8）发车进路走行时间tlp：自列车k开始占用过站径路p∈Pk的发车进路l时起至该列车尾部出清发车进路时止的时间。

（9）接入时刻trk：列车k接车进路开始办理的时刻。

（10）tfk：列车k发车进路开始办理的时刻，通过列车和非通过列车不同。

（11）到达时刻tak：非通过列车k在到发线上停稳的时刻或通过列车k头部经过停车位置标的时刻。

（12）出发时刻tdk：非通过列车k自到发线上启动的时刻或通过列车k头部经过停车位置标的时刻。

（13）发出时刻tlk：列车k尾部出清发车进路的时刻。

令xk,p为0-1 变量，当列车k占用过站径路p时，xk,p= 1，否则xk,p= 0。令θk为0-1 参数，当列车k为通过列车时，θk= 1，否则θk= 0。根据图3、图4，上述各时刻、时段的关系如下，式中∀k∈K，p∈Pk：

2.3.3 到发线占用相容性约束

所有列车的过站径路必须相容，包括到发线占用相容，即任意两列列车先后占用同一条到发线时，前行列车出发一段时间后，后行列车才能开始占用该条到发线所在过站径路的接车进路。这里的一段时间即到发线占用安全间隔时间ρ。令Uk,h为0-1 变量，当列车k先于列车h占用到发线时Uk,h=0，否则Uk,h=1。令M为足够大正数，其中∀k∈K，∀h∈K，k≠h，∀p∈Pk∩Ph，则：

2.3.4 咽喉区进路占用相容性约束

所有列车的过站径路必须相容，包括咽喉区进路占用相容，即所有列车占用咽喉区进路时不能存在时空冲突。文献[16]引出“冲突度（Degree of Conflict，DOC）”的概念计算敌对进路的解锁时间；文献[17]给出了车站进路“封闭-解锁”的3 种模式下，时间冲突度的计算公式；文献[18]给出了车站进路“一次封闭，分段解锁”模式下，时间冲突度计算的近似方法，并利用其计算了郑州东站、西安北站车站咽喉区进路的时间冲突度。若进路α与进路β为敌对进路，则进路α与进路β的时间冲突度γα,β表示进路α开始占用γα,β时间后，进路β才能开始占用。对于∀k∈K，∀h∈K，k≠h，∀p∈Pk，∀q∈Ph，共有以下4类时间冲突度：

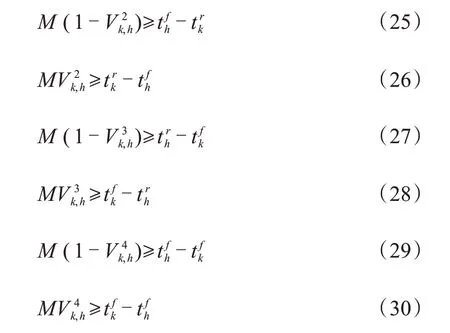
2.3.6 在车站立即折返或进行终到、始发作业，同

一交路上共用车底的前后两列列车相关约束

2.3.7 换乘约束

3 种换乘方式的换乘接续列车径路对须满足列车占用到发线唯一性约束与列车过站径路占用相容性约束。3种换乘方式的约束如下：

2.3.8 到发线运用图定方案改变限度约束

令ck,p为0-1 参数，当列车k的过站径路p中的到发线为其图定到发线时ck,p=1，否则ck,p=0，kmax为集合K的列车总数。到发线运用图定方案改变程度D的计算公式如下：

综合2.2 目标函数与2.3 约束条件，可构建面向站内换乘便捷性的到发线运用优化研究问题的多目标混合整数线性规划模型：

目标函数：式（1）～（4）

约束条件：式（5）～（44）

面向站内换乘便捷性的到发线运用优化问题是到发线运用方案编制层面的问题，对求解时间要求不高，故可直接调用商业求解器CPLEX，寻找精确解以保证解的质量。

3 算例分析

本部分选取郑州东站真实站场数据及2021年12 月10 日11 时至15 时高峰时段139 列列车的真实数据进行实验验证。图5 为郑州东站咽喉区与到发线示意图，郑州东站设有32条到发线，30个站台面（站台面编号与到发线编号一致，Ⅹ、Ⅺ为不邻站台的正线，不设站台面），其中到发线1～16 为京广场，17～20为城际场，21～32为徐兰、郑渝、预留郑济场。郑州东站衔接北京、广州、徐州、西安、重庆、郑州、新郑机场、宋城路等方向，另有太原方向经郑州方向引入，阜阳方向经重庆、新郑机场方向引入。郑州东站配备郑州东动车组运用所。图6为郑州东站引入方向与到发线衔接关系示意图。郑州东站共有接车进路133 条、发车进路112 条，各进路走行时间由进路长度、列车长度、列车运行速度共同确定，限于篇幅不再展示。郑州东站咽喉区进路采用“一次封闭，分段解锁”模式，进路办理时间σl取30 s，前后两列列车占用同一到发线安全间隔时间ρ取180 s，前后两列列车占用接发车进路的时间冲突度γα,β根据文献[18]给出的方法计算得到，列车到发线走行时间σc取30 s。139 列列车中，始发列车1 列，终到列车1 列，停站列车93列，立即折返列车19 对共38 列，在郑州东站进行终到、始发作业，属于同一交路共用车底的前后两列列车3 对共6 列。所有列车经过郑州东站均停站，故算例中不包含通过列车。各列车详细信息限于篇幅不再展示。

图5 郑州东站咽喉区与到发线示意图Fig.5 Station yard at Zhengzhoudong Railway Station

图6 郑州东站引入方向与到发线衔接关系Fig.6 Train’s inbound and outbound directions when it occupys an arrival-departure tracks of Zhengzhoudong Railway Station

图7 为车站到发线运用图定方案。图中淡绿色梯形代表列车，梯形左上点代表列车到达时刻，梯形右上点代表列车出发时刻，梯形左下点代表列车接车进路开始办理时刻，梯形右下点代表列车尾部出清发车进路时刻。梯形上数字为列车编号，其中13（120）表示这是一对折返列车或在车站进行终到、始发作业的同一交路上共用车底的前后两列列车。

图7 到发线运用图定方案示意图Fig.7 Schematic of original arrival-departure tracks utilization schedule

图8为到发线运用图定方案中列车换乘接续关系示意图。图中淡金色圆点（以列车到达时刻表示）代表列车，两圆点间浅蓝色带箭头线段代表两列列车是一对可供旅客选择的短距离站厅换乘接续列车对，箭头由换乘列车指向接续列车。同理，紫色带箭头线段代表两列列车是一对可供旅客选择的同台异面换乘接续列车对。黑色带箭头线段代表两列列车是一对可供旅客选择的同台同面换乘接续列车对。在统计换乘接续列车对数时，将一对折返列车或在车站进行终到、始发作业的同一交路上共用车底的前后两列列车视为两列车，如图中13、120，前车用其到达时刻表示，后车用其出发时刻表示。

图8 到发线运用图定方案中列车换乘接续关系示意图Fig.8 Schematic of transfer-connection train pairs in original arrival-departure tracks utilization schedule

3.1 到发线运用图定方案可优化空间分析

图8 中，无列车对实现同台同面换乘，仅有列车23 占用到发线28 与列车121 占用到发线29，列车41占用到发线30与列车44占用到发线31，列车81 占用到发线21 与列车130 占用到发线20，列车102 占用到发线17 与列车99 占用到发线16，共4对列车实现同台异面换乘。 6 种细分类型的短距离站厅换乘列车对数共有154对。

在处理器为11th Gen Intel(R) Core(TM) i7-11700K @ 3.60GHz 3.60 GHz，内存为16GB 的个人计算机上，调用商业求解器CPLEX12.6.2，设置到发线运用图定方案改变限度，分别以同台同面换乘接续列车对数最多、同台异面换乘接续列车对数最多、短距离站厅换乘接续列车对数最多为目标求解模型，结果如表3所示。

由表3可知：

（1）在郑州东站，旅客进行同台同面换乘的难度极大。究其原因，郑州东站当前到发线固定使用方案严格、清晰。不同引入、发出方向的列车无法占用同一条到发线。因此，对郑州东站基于到发线运用优化提升旅客换乘便捷性不再考虑同台同面换乘方式。

（2）分别以上述3 个目标求解模型，在到发线运用图定方案改变程度D＜90%的情况下，均得到明显优于到发线运用图定方案的最优解，说明郑州东站到发线运用图定方案的旅客换乘便捷性存在较大优化空间，本文构建的模型是有效的。

3.2 Dmax灵敏度分析

根据同台同面换乘、同台异面换乘、短距离站厅换乘对旅客的便捷程度，以及短距离站厅换乘接续列车对数在到发线运用图定方案中数量众多，将3种换乘方式的权重系数设置为α=0，β=100，η=1。根据算例中139 列列车经停312 个车站的日停站列车数，计算每一个换乘接续列车对的权重系数λk1,k2。设置不同到发线运用图定方案改变限度Dmax，分析模型的优化效果，实验结果见表4、图9。

由表4与图9可知：

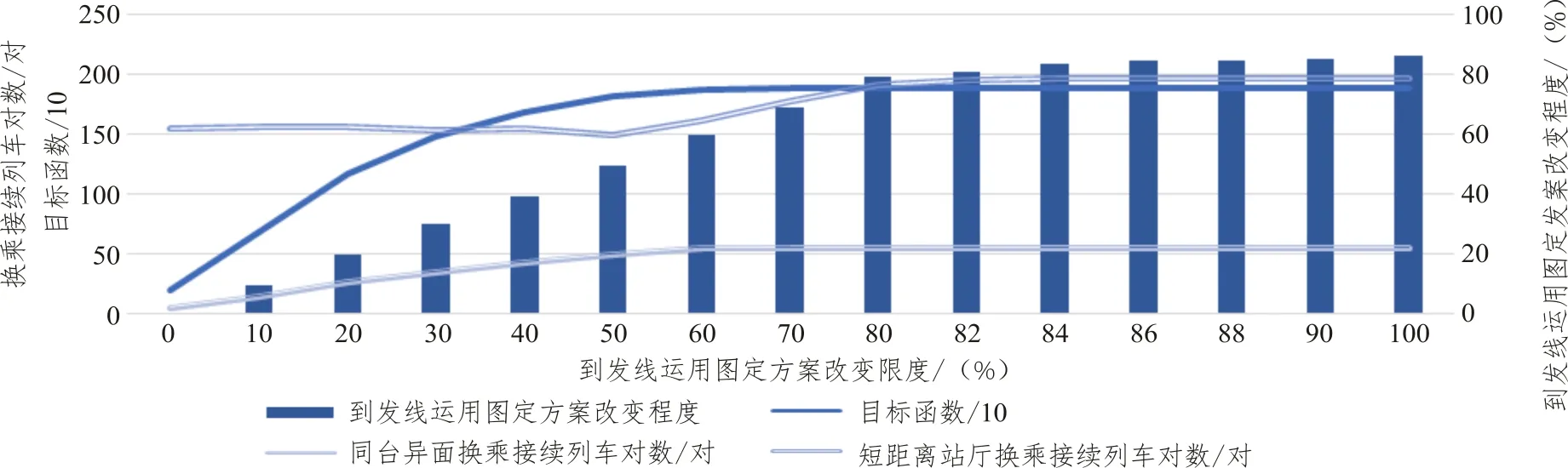
图9 不同Dmax实验结果Fig.9 Experimental results under conditions of different Dmax

表4 不同Dmax实验结果Tab.4 Experimental results under conditions of different Dmax

（1）随到发线运用图定方案改变限度Dmax增大，同台异面换乘接续列车对数在Dmax增至60%后保持55 对不变；短距离站厅换乘接续列车对数在Dmax增至84%后保持197 对不变；目标函数在Dmax增至86%后保持不变。由此说明模型在Dmax增至84%～86%时已取得当前权重下的最优目标。

（2）在到发线运用图定方案改变限度Dmax增至84%前，到发线运用图定方案改变程度D和到发线运用图定方案改变限度Dmax保持一致，呈线性增长趋势。究其原因，在Dmax增至84%前，Dmax是模型最优解的影响因素。在此阶段，模型通过改变列车的图定过站径路的方式，随Dmax增大不断提升目标函数值。

（3）在到发线运用图定方案改变限度Dmax增至84%后，到发线运用图定方案改变程度D和到发线运用图定方案改变限度Dmax不再保持一致，出现趋于平缓的趋势。究其原因，在Dmax增至84%后，Dmax不再是模型最优解的影响因素。模型不能通过改变更多列车的图定过站径路的方式来提升目标函数值。由此说明本文建立的模型具有一定的对称性，模型的可行解具有同质性。在Dmax增至84%后，D不同的较多可行解均能得到同一最优目标。

（4）在到发线运用图定方案改变限度Dmax=40%时，求解模型得到同台异面换乘接续列车对数为42 对，相较于到发线运用图定方案提高了950%；短距离站厅换乘列车对数为154 对，与到发线运用图定方案保持一致。考虑到发线运用图定方案改变程度D越小对车站作业秩序影响越小，且继续增大Dmax模型优化效果提升较小，设置Dmax= 40%得到的到发线运用优化方案能较好兼顾旅客、车站双方利益。

到发线运用图定方案改变限度Dmax= 40%时，到发线运用优化方案如图10，图中淡金色梯形代表图定到发线发生改变的列车，浅绿色梯形代表图定到发线未改变的列车。

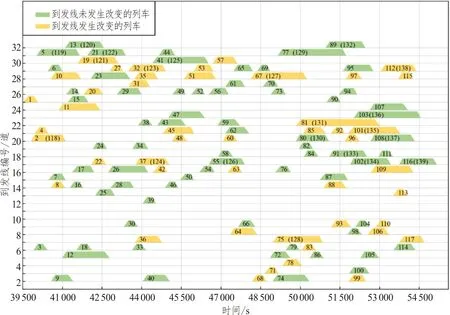
图10 Dmax = 40%到发线运用优化方案示意图Fig.10 Schematic of optimized arrival-departure tracks utilization schedule when Dmax = 40%

图11为到发线运用优化方案中列车换乘接续关系示意图。图中存在双向箭头线段，如列车64和66 之间的紫色双向箭头线段，表示此换乘接续列车对的到达出发时间间隔合适，可双向换乘。

图11 Dmax = 40%到发线运用优化方案中列车换乘接续关系示意图Fig.11 Schematic of transfer-connection train pairs in optimized arrival-departure tracks utilization schedule when Dmax = 40%

4 结束语

本文基于集合划分，构造了列车可行过站径路集、换乘接续列车径路对集。考虑列车种类、接入发出方向、到发时间间隔及换乘接续列车对停靠到发线距离等多方面因素，构建了3种换乘方式的换乘接续列车径路对集，实现了最大限度保证存在换乘客流的换乘接续列车对被选择，保证旅客换乘安全、换乘走行时间与走行距离更加匹配，更加符合大型高铁站实际情况的目的。本文基于构建的过站径路集、换乘接续列车径路对集以及到发线运用优化模型，加入换乘约束，建立面向站内换乘便捷性的到发线运用优化问题的多目标混合整数线性规划模型，并加入有效不等式约束改进模型求解效率。郑州东站实例验证表明本文构建的模型可有效提升旅客在大型高铁站内换乘的便捷性，并兼顾车站利益，具有实际意义。

下一步，将从以下3方面继续深入：①进一步完善换乘接续列车径路对集的构造方法；②优化模型目标函数，根据换乘接续列车对能服务的OD 范围及客流需求，给每一个换乘接续列车对设置更加合理的权重，使模型目标函数更加合理；③探索解决列车晚点等因素造成列车径路对换乘接续关系改变，影响旅客换乘便捷性的方法。