钢筋混凝土烟囱爆破拆除的下坐及早期断裂预测*

孙金山，谢先启，贾永胜，姚颖康，刘昌邦，韩传伟，王洪刚，黄小武

（1. 江汉大学精细爆破国家重点实验室，湖北 武汉 430056；2. 江汉大学爆破工程湖北省重点实验室，湖北 武汉 430056；3. 武汉爆破有限公司，湖北 武汉 430056）

目前，废弃的钢筋混凝土烟囱主要采用爆破技术拆除。近年来，在拆除约180 m 的高烟囱时，部分烟囱会发生严重的下坐问题，并在起爆后不久发生中部断裂，且上、下段有时会发生分离，上段烟囱的倒塌方向可能失控，而由于下段烟囱的重心位置发生了改变，容易导致烟囱下半段向相反方向倒塌或“炸而不倒”（如图1～2 所示），该现象可能导致严重的安全事故。

图1 萧山热电厂180 m 高烟囱Fig. 1 The 180-m-high chimney of Xiaoshan thermal power plant

图2 成都热电厂210 m 高烟囱Fig. 2 The 210-m-high chimney of Chengdu thermal power plant

烟囱爆破拆除过程涉及爆破切口形成、支撑区破坏、应力重分布和结构动力响应等诸多方面，其力学机制较复杂。针对烟囱爆破切口形成后支撑部位的破坏机制问题，褚怀保等观测了爆破切口形成后保留筒壁的受力状态，认为爆破切口形成后存在0.5～3.0 s 的荷载重新分布和中性轴形成的过程。郑炳旭等观测了6 座钢筋混凝土烟囱切口的支撑区，认为支撑区在爆破后承受自重突加的荷载，容易引起烟囱下坐；切口端先受压破坏，而后中性轴受拉，呈现大偏心受压脆性断裂特征。郑炳旭等还分析了切口自重突加载荷引起的支撑区受压范围，认为切口圆心角宜取210°～230°。徐鹏飞等认为爆破切口形成后2～3 s 的中性轴稳定时间是烟囱预防过早下坐和形成定向倾倒趋势的关键。言志信等建立了钢筋混凝土烟囱爆破后支撑区的应力计算模型，提出引入冲压系数来考虑突加荷载的影响。

针对高烟囱爆破过程中的“空中折断”问题，杨建华等建立了烟囱任一截面的内力分布和极限承载力模型，认为高度超过150 m 的钢筋混凝土烟囱在倾倒角度超过40°后，均可能在离顶部约1/3 高度处发生断裂，烟囱越高，折断发生的时间越早。言志信等认为烟囱折断发生的位置和时间与切口形状及材料的力学性能密切相关。唐海等认为烟囱在倾倒过程中主要发生弯曲破坏，首次折断的部位约在距离顶部1/3 高度处，强度不大的烟囱可能会有多次折断。侯吉旋等认为质量均匀分布烟囱的断裂点距离顶部1/3 处，而对于上细下粗的烟囱，断裂点将会下移。

针对烟囱结构在纵波作用下的动力响应问题，王云剑实验研究了烟囱断裂位置与冲击波作用周期和烟囱固有周期之间的关系。Pallarés 等采用三维有限元模型分析了砌体烟囱在地震作用下的破坏现象，得到了结构的破坏模式、最大应力和位移特征。Wolf 等研究了核电站典型烟囱在地震和冲击荷载作用下的响应特征。Wilson根据10 座烟囱在地震作用下的非线性特征，提出了钢筋混凝土烟囱的非线性动力分析方法。Huang 等根据高115 m 钢筋混凝土烟囱的地震动力响应，提出了一种新的三维推覆分析方法。Minghini 等对地震中砖砌烟囱破坏问题进行了分析，阐述了烟囱上部的剪切破坏机制。

综上所述，对钢筋混凝土烟囱爆破拆除的失稳、倒塌、运动过程以及烟囱地震响应等问题已有大量研究，但对烟囱在爆破拆除过程中的下坐及其诱发的早期断裂问题研究较少。本文中将通过对一座高180 m 的钢筋混凝土烟囱的运动和断裂过程的观测，对烟囱爆破拆除的下坐和早期空中断裂现象进行分析讨论，研究失稳、下坐和早期断裂的判别或预测方法。

1 烟囱下坐及其诱发空中断裂的案例

1.1 爆破方案

爆破拆除的钢筋混凝土烟囱高180 m，0～25 m 高程混凝土标号为C40，25～180 m 高程混凝土标号为C30，烟囱主要结构尺寸见表1。烟囱横截面轴向配筋为双层配筋，环向配水平箍筋。7.25 m 高程处分布有2 个烟道口并设有积灰平台，大烟道尺寸为5.9 m×10.4 m，小烟道尺寸为5.9 m×5.4 m；东、西方向各有2 个检修门，尺寸均为2.4 m×2.4 m，如图3 所示。

表1 烟囱主要结构尺寸Table 1 Structure parameters of the chimney

烟囱采用正梯形爆破切口，如图3 所示。切口高4.4 m，布设在烟囱底部0.5 m 高程处，爆破切口的圆心角为220°，底边展开长30.95 m。切口两侧布设定向窗，底边长3.0 m，张开度为30°。爆破前用钢筋混凝土对西侧检修门进行封堵。爆破切口区共布置634 个炮孔，乳化炸药总装药量为136 kg，炮孔内安装延期时间为3 400 ms 的导爆管雷管。

1.2 监测方案

为分析烟囱的失稳破坏过程，在烟囱支撑区外侧布置一套动态摄影测量系统。该摄影测量系统由高精度工业相机、基准尺、测量标志、计算软件和电脑组成，先利用测量相机采集目标点的坐标值，再利用目标点做点线面的标准拟合等。将2 台工业相机对称安装在支撑区背侧地面的支座上（见图3），相机分辨率4 872×3 248，采集频率1 000 s。经标定，动态摄影测量系统的测量误差标准值小于3 mm。

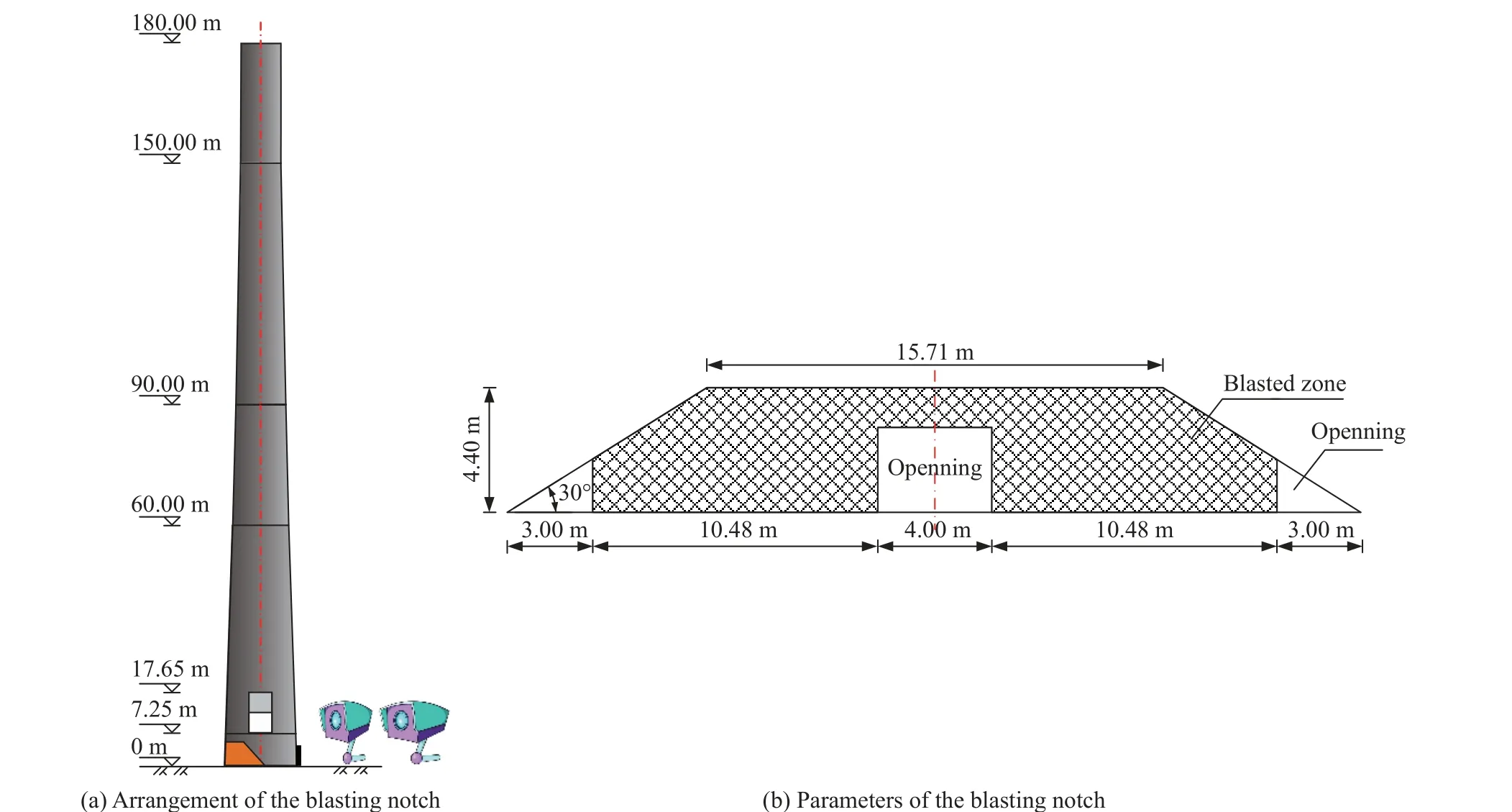
图3 爆破方案Fig. 3 Blasting plan of the chimney

同时，在支撑区外围地面上布置2 个分辨率1 280×960、采集频率25 s的普通监控摄像头。在爆破远区，则采用无人机在空中对爆破过程进行视频录像。

1.3 下坐过程

由爆破过程的监测视频可知，起爆后切口两侧的混凝土受到强烈挤压而发生破坏。起爆后约0.5 s，支撑区产生了与水平方向夹角为45°的裂缝（见图4(a)），伴随着主裂缝的扩展，大量的混凝土不断从筒壁挤出、脱落；起爆后约1.2 s，裂缝沿着混凝土薄弱部位扩展（见图4(b)）；起爆后约1.8 s，支撑区的主裂缝贯通（见图4(c)）；起爆后约2.5 s，爆破切口完全闭合（见图4(d)）。

图4 烟囱支撑区裂纹扩展过程Fig. 4 Crack propagation process in the support part

监测结果显示，在支撑区后部裂缝扩展较快，混凝土破坏也较严重。在裂缝产生、扩展至贯通的过程中，支撑区后部未观测到明显的拉裂缝产生，表明该烟囱支撑区的破坏方式主要是压剪破坏。

烟囱贯穿裂缝形成后，支撑区无法承受上部结构的荷载而发生整体下坐。下坐过程中，烟囱筒体不断与底部残余结构及地面发生剧烈碰撞，筒体底部混凝土被压碎、挤出，并堆积在烟囱周围。起爆约4.0 s 后，烟囱下坐过程结束。整个下坐过程中，烟囱下坐速度先增大，然后迅速减速至0，共历时约2 s，下坐总高度约10 m。与此同时，烟囱在下坐过程中还产生了轻微转动，但总体转动角度不大，下座结束时烟囱转动角度大约为3°。

通过摄影测量，获得了烟囱下坐过程的位移时程曲线，如图5 所示。测量数据表明，烟囱爆破后下坐量先随时间缓慢增长，随后快速增加，最后则逐渐停止。将下坐位移时程曲线对时间进行一次和二次微分后，可以近似获得下坐速度(见图6)和加速度时程曲线(见图7)。在下坐开始后的1.0～1.5 s，下坐速度可达10 m/s，而向下运动的加速度最大可接近10 m/s。下坐运动减速时，向上的加速度最大可接近30 m/s。因此，烟囱在下坐过程中可能经历多次“失重”和“超重”效应。而“失重”和“超重”的变换速度较快，将在烟囱中诱发压缩应力波，可能造成烟囱的持续下坐。当下坐量较大时，底部破碎的钢筋混凝土能起到显著的缓冲作用，“超重”效应逐渐减弱，直至下坐停止。

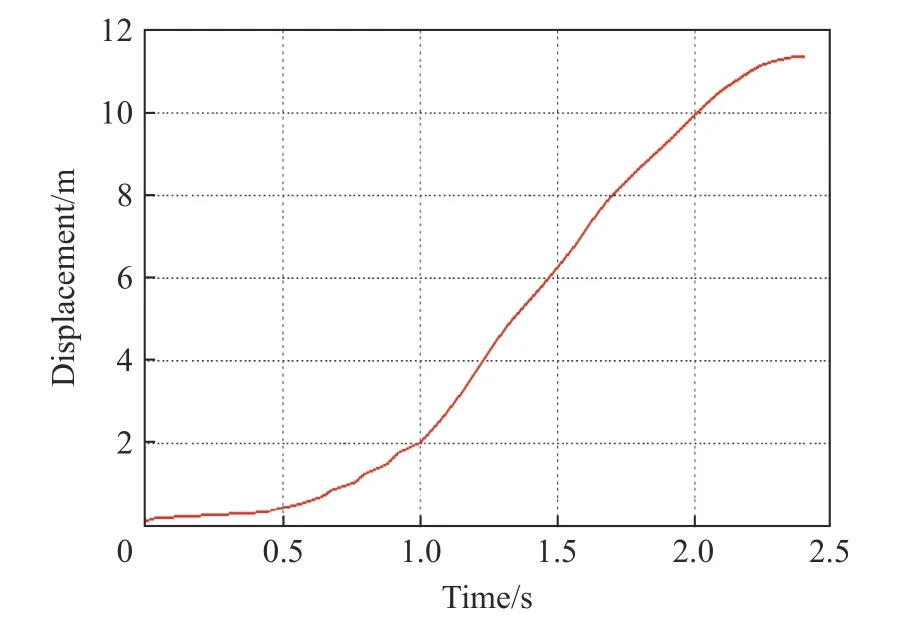
图5 烟囱下坐位移时程曲线Fig. 5 Displacement-time history curve of chimney sinking down

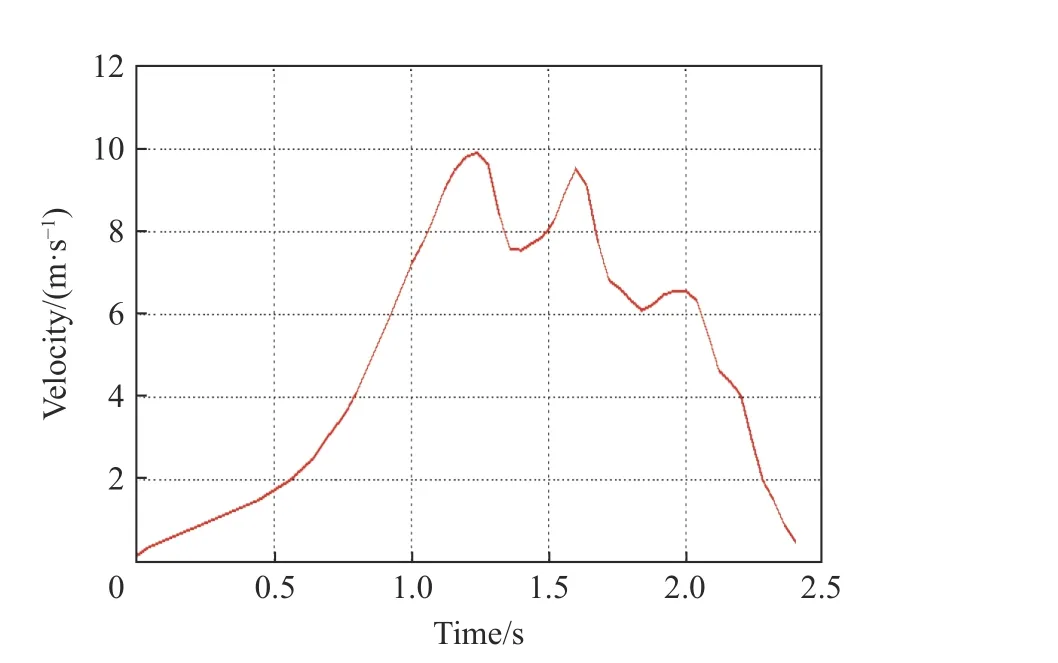
图6 烟囱下坐速度时程曲线Fig. 6 Velocity-time history curve of chimney sinking down

图7 烟囱下坐加速度时程曲线Fig. 7 Acceleration-time history curve of chimney sinking down

1.4 空中断裂过程

烟囱在下坐结束时，在其中部发生了断裂，断裂位置约在90 m 高程处。断裂后的上半段筒体继续向原倒塌方向发生转动。起爆后约12 s 时，烟囱上、下两部分筒体分离，上部分筒体在其原初速度的基础上加速下落；下部分筒体由于重心位置未偏出筒体的投影区且倾倒动能不足，导致无法继续倾倒（见图8(d)）。

图8 烟囱空中折断过程Fig. 8 Breaking in the air of the chimney

2 烟囱失稳下坐的预测

2.1 失稳下坐时支撑区演化过程

根据烟囱支撑区的受力特征与现场观测结果，同时考虑混凝土受压破坏过程的全应力-应变曲线特征（见图9），支撑区的失稳下坐过程可分为以下4 个阶段。

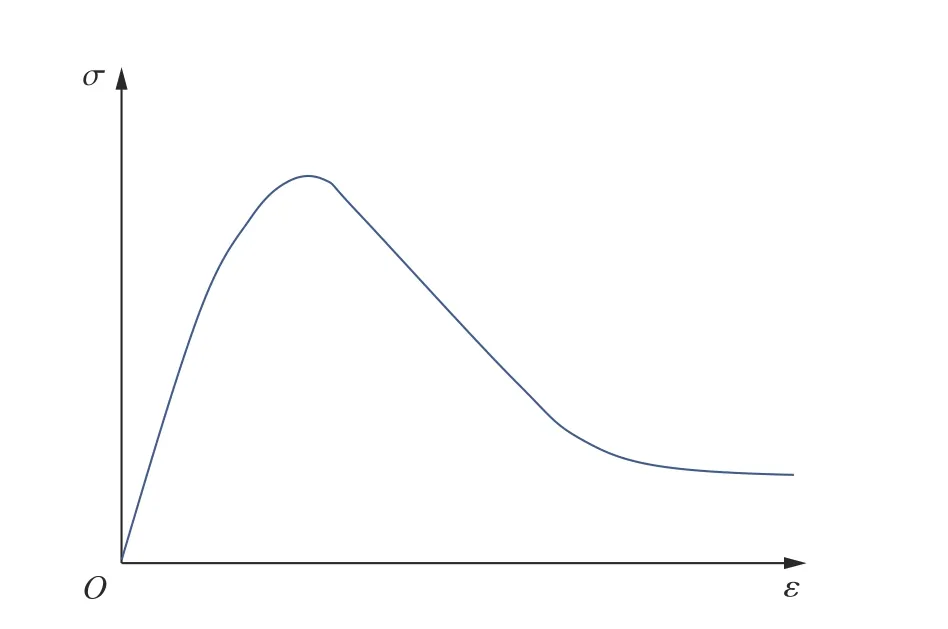
图9 混凝土典型应力-应变曲线Fig. 9 Typical full strain-stress curve of concrete

（1）起爆后应力瞬态调整

爆破切口形成瞬间，支撑区将发生应力瞬态调整，爆破切口部分承受的荷载将迅速向支撑区混凝土上转移。

（2）支撑区正截面抗弯承载力达到峰值

应力瞬态调整完成后，保留的支撑区变为大偏心受压构件(见图10(a))。钢筋与混凝土将发挥材料最大承载性能以抵抗倾覆力矩和竖向压力。根据大偏心受压构件的受力变形特点，在支撑区横截面上距离中性轴最远位置处的应力和应变最大，同时，由于混凝土的屈服应变远低于钢筋的屈服应变，靠近定向窗的支撑区混凝土最先发生压缩屈服，此时整个截面的抵抗力矩达到峰值或接近峰值（见图10(b)）。若支撑区抵抗力矩大于倾覆力矩则混凝土将不再进一步破坏，烟囱则不能顺利倾倒；若支撑区抵抗力矩小于倾覆力矩则混凝土将进一步破坏，烟囱则可继续发生转动。

（3）支撑区正截面受压承载力达到峰值

当烟囱失稳倾覆时，随着其转动角度的增大，支撑区截面上的应变将持续增大，且中性轴位置发生变化。当支撑区中性轴消失时，整个支撑区横截面均呈受压状态。由混凝土的全应力-应变曲线特征可知，混凝土达到屈服状态后，随着应变的增大其承载能力将不断降低直至达到一定的残余强度，变为塑性材料。因此，中性轴刚刚消失时，截面上各处混凝土的压应力分布与其应变相对应，分别处于混凝土全应力-应变曲线的不同应力值，此时支撑区断面达到其最大竖向承载力（见图10(c)）。

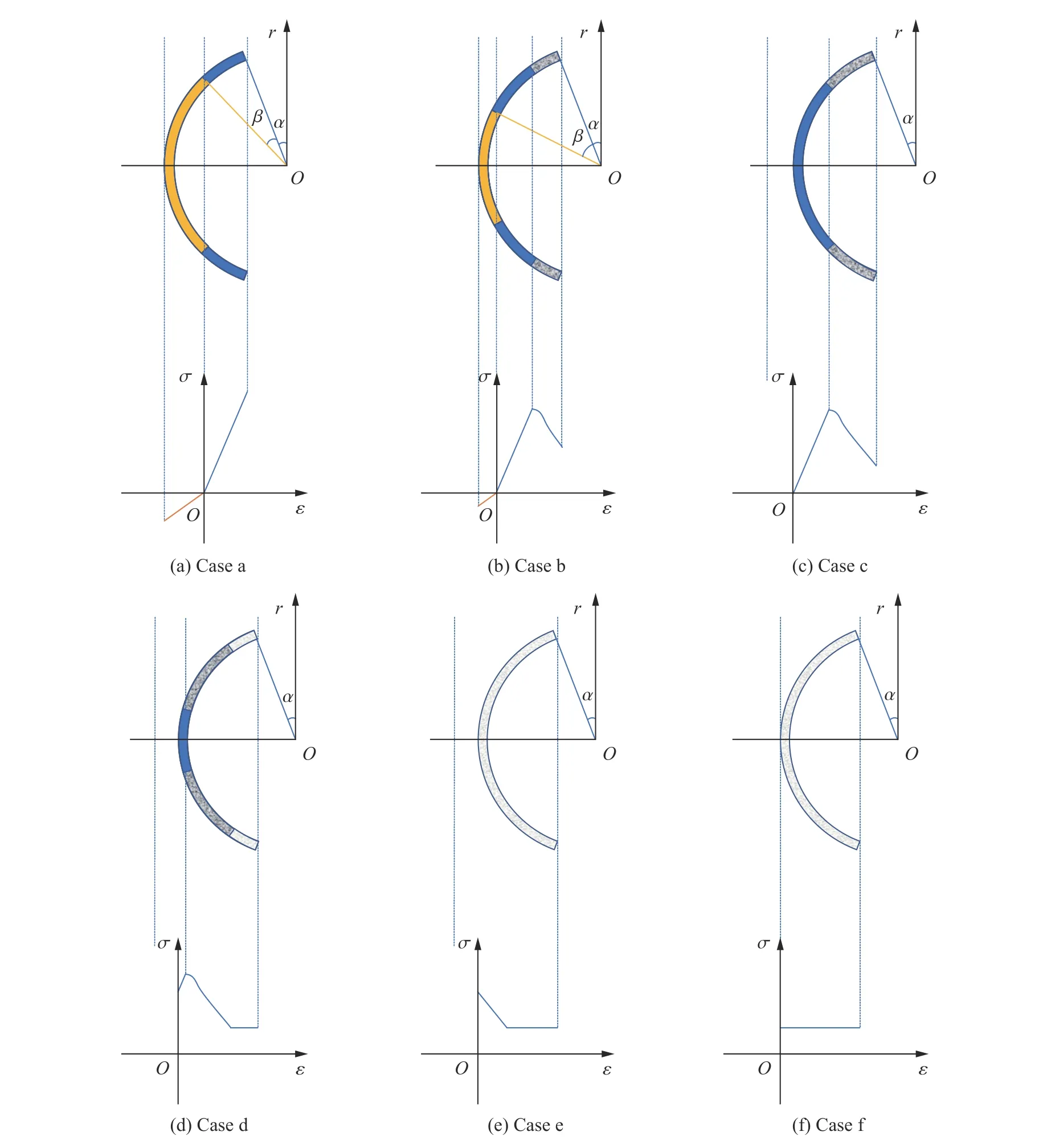
图10 支撑区不同区域混凝土的应力与应变状态示意图Fig. 10 Schematic of the stress and strain status of the concrete in the support part

（4）支撑区塑性铰的形成或下坐

受倾覆力矩的作用，混凝土的应变还将持续增大，因此一般情况下整个支撑区最终将变成“塑性铰”，此时，支撑区的混凝土仅剩余残余承载力（见图10(d)～(f)）。当烟囱的重量小于或等于支撑区的残余承载力时，烟囱则匀速破坏、缓慢下坐、持续转动。当烟囱重量大于支撑区竖直向残余承载力时，烟囱将获得一定的竖向加速度进而向下加速下坐，并同步发生转动，但由于下坐速度快、历时短，下坐过程中烟囱偏转角度一般较小。

2.2 支撑区受力及失稳判别

爆破拆除烟囱时，为了提高爆破切口设计的可靠性，需对不同设计方案进行对比和失稳判别。为了简化计算，传统的失稳判别力学模型通常假定受拉区和受压区完全达到极限承载状态，这与支撑区的实际受力状态存在显著差异。支撑区中性轴附近的应力和应变均较小，而在前后边缘处应变最大（但应力不一定最大）。

在起爆后的短时间内，支撑区筒壁处于低应变状态，因此，可认为中性轴处竖向应变为0，中性轴两侧混凝土的应变与到中性轴的距离呈线性关系。即混凝土受压区外边缘屈服应变为ε，将逐渐减小至中性轴处的0。

式中：δ 为支撑区筒壁的厚度，为混凝土的弹性模量。

同理，已知支撑区筒壁单根钢筋的极角时，也可得到单根钢筋的压力、拉力及其合力。但是在爆破设计过程中钢筋的定位难度较大，逐根钢筋的受力计算也较繁琐，因此可将钢筋网等效为薄壁圆筒进行计算。忽略钢筋保护层厚度时，将钢筋网等效为钢筒后，等效钢筒壁厚δ和δ可表示为：

式中：为钢筋的弹性模量。

同理，支撑区的受拉区混凝土受到的竖向拉力为：

受拉区钢筋受到的竖向拉力为：

需要指出的是，爆破后切口区裸露的钢筋骨架也具有一定的承载能力，但在工程实践中爆破切口高度往往较高，且爆炸荷载会使竖向钢筋发生弯曲。因此，爆破后切口区的钢筋骨架竖向承载能力较低时，其贡献的竖向承载力可忽略。

假定应力重新调整后，烟囱处于临界失稳状态，且受压区边缘应变恰好达到屈服应变，此时烟囱处于静力平衡状态，且未发生加速转动，则烟囱的重量与支撑区竖直向力的合力为0，得到平衡方程：

式中：为烟囱的总重量。

将式（2）、（4）～（6）代入式（7）并化简得：

式（8）为超越方程，无解析解。为了方便工程应用，利用泰勒级数对三角函数进行展开，化简后解得β 的近似解为：

式中：

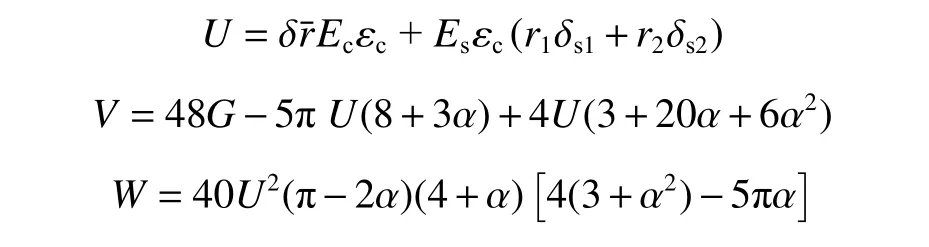
在工程设计过程中，先初步确定α 后可通过试算法解得方程（8）的中受压区对应的弧度β，或通过近似解（9）计算β，进而可确定中性轴位置，并可进一步对烟囱能否失稳进行验算。

烟囱要打破静力平衡状态而发生加速转动时，重力形成的倾覆力矩要大于抵抗力矩。忽略受拉区混凝土产生的抵抗力矩时，烟囱的失稳条件为：

定义倾覆失稳系数为：

由式（10）～（12）、（14）可计算烟囱的失稳系数。

根据混凝土应力应变特征及其在支撑区横截面上的分布规律，设支撑区边缘处混凝土刚进入塑性状态时，=1；假定受压区全部进入塑性状态且混凝土材料为理想弹塑性材料时，=2；假定受压区一半面积进入塑性状态且混凝土为理想弹塑性材料时，=1.5。显然，=1.5～2 时可满足失稳的要求。而＞2 时倾覆力矩过大，可能导致支撑区快速压溃而发生下坐。

2.3 烟囱下坐预测

根据3.1 节的分析，烟囱支撑区满足倾覆失稳条件后，将发生加速转动，而由于钢筋混凝土的不断屈服，其抵抗力矩将变得越来越小，因此截面的中性轴将不断发生移动以发挥材料的最大承载能力，当钢筋最终被拉断或者中性轴消失时，支撑区正截面将主要受压缩作用。

混凝土在受压屈服后，承载能力将随着应变的增大而持续降低，最终将达到其残余承载力。由于烟囱爆破切口常常采用正梯形切口，会形成变截面的支撑区，因此设支撑区下侧最小截面面积为，上侧最大截面面积为，则支撑区残余承载力与烟囱重量存在以下3 种关系。

（1）烟囱重量大于支撑区最大残余承载力时，会发生显著加速下坐直至支撑区完全压溃消失。支撑区和爆破切口消失后，如新形成的断面较为平整，则烟囱重心在水平面的投影落在新截面的形心附近，倾覆力矩将急剧减小甚至消失，烟囱可能发生炸而不倒的现象，其判别条件表示为：

式中：σ为支撑区混凝土的残余强度，为支撑区上侧最大截面面积（采用正梯形切口时）。

（2）烟囱重量大于支撑区最小残余承载力，且小于最大残余承载力时，烟囱先发生加速下坐直至重量和支撑区残余承载力相等时再发生减速下坐，直至达到新的平衡。此时，支撑区可能部分保留，也可能因烟囱惯性力作用而全部压溃，因此，顺利倾倒和炸而不倒的现象均可能发生，其判别条件表示为：

式中：为支撑区下侧最小截面面积（采用正梯形切口时）。

（3）烟囱重量小于支撑区最小残余承载力时，烟囱因支撑区混凝土的压溃挤出而发生向下的位移，可能会发生短暂的下坐，但支撑区残余截面的不断增大将阻止下坐的进一步发生，使烟囱得以顺利倾倒，其判别条件表示为：

3 下坐诱发空中断裂的预测

烟囱空中断裂现象的宏观特征表明，发生下坐现象时支撑区底部截面将与基础碰撞，碰撞接触面上必然产生较高的动态压应力和应变并向烟囱顶部传播。假设烟囱筒体中有一压缩应力波传播，仅分析烟囱切口以上且远离切口区的部分时，该部分可简化为经典的变截面一维直杆力学模型。同时，仅考虑一个波动信号从底端到达顶端的应力波传播过程时，可忽略波在两端边界处的入射和反射等过程，进而可方便地对其动力学过程进行理论求解。

因此，当烟囱下坐导致切口闭合、支撑区消失时，在烟囱烟道口以上部分的横截面上将作用一个轴向脉冲荷载，在满足平截面假定条件时，取烟囱的一段微元体进行分析，如图11 所示。

图11 不受应力集中效应影响的烟道口以上烟囱的微元体模型Fig. 11 Microelement model of the chimney above the flue without stress concentration effect

根据达伦贝尔原理，微元体的受力平衡方程可表示为：

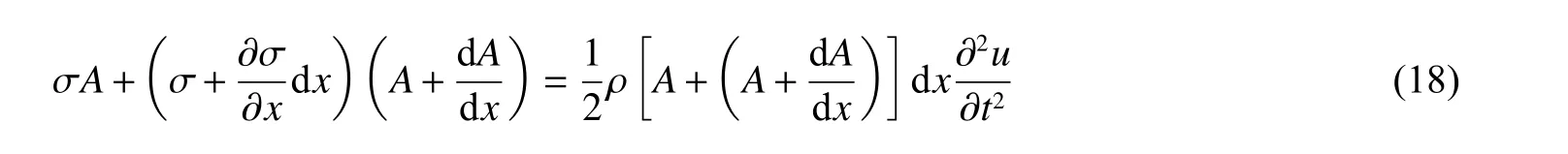
式中：σ 为烟囱横截面上的竖向应力，为烟囱的横截面面积。为获得微分方程的解，设烟囱截面随烟囱高度连续变化，可表示为：

式中：κ、λ 为系数，为横截面距离地面的高度，为烟囱总高度。

将式（19）代入式（18）中，化简并略去高阶项后，式（18）简化为：

在式（24）中，v为变量，需确定其数值方可求解波动方程。设=0 时，烟囱的运动速度为，并逐渐降低至0。根据碰撞冲击作用过程的特征，且为了便于方程的求解，以三角函数拟合的v为：

式中：为烟囱速度由降低至0 时所经历的时间。

根据3.3 节的分析，烟囱在下坐过程中，需克服支撑区的残余承载力而发生加速运动，其加速度为：

式中：为支撑区截面面积（可取平均值）。

设下坐高度为，根据运动距离、速度和加速度间的关系，可表示为：

由式(26)～(27)可得：

烟囱速度由降低至0 的过程中，设为基础提供的减速阻力，根据动量守恒原理得：

烟囱下坐后筒壁与基础的接触面为整个圆环形截面时，接触面上的力先增大，直至达到混凝土的动态屈服强度后，再减小至烟囱的重量。因此，取接触力的近似平均值时，的取值范围为：

式中：σ为混凝土的抗压强度，η 为混凝土的抗压强度动态提高系数，为烟囱底端筒壁的横截面面积。由式(28)～(30)得到的取值范围为：

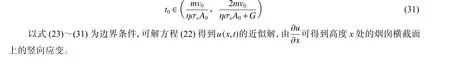
根据式(22)～(31)，可对下坐一定高度的烟囱进行动力学分析，估算烟囱横截面上的应变值，当一定高度范围内筒壁的应变均大于混凝土的压缩屈服应变时，则可判定烟囱将发生早期空中断裂现象。

4 案例分析与讨论

以第1 节中的高180 m 的烟囱为例对预测模型进行验证。该烟囱质量约8 600 t，重量约84.28 MN，截面面积函数中κ=24.5、λ=1.5。混凝土密度取2 500 kg/m，混凝土屈服强度标准值取σ=26.8 MPa，弹性模量取=32.5 GPa，泊松比取0.17，钢筋弹性模量取200 GPa。切口烟囱底端外半径为8.12 m，内半径为7.57 m，壁厚0.55 m。爆破切口设计圆心角 ω =220°，支撑区下边缘展开长度约33.56 m，截面面积18.46 m；上边缘展开长度约18.31 m，截面面积10.07 m。外侧钢筋截面面积为254.5 mm，内侧钢筋截面面积为153.9 mm，间距均为0.2 m。爆破切口参数如图3 所示。

4.1 失稳判别

根据式（9）～（10），可在初选切口圆心角后对支撑区中性轴位置进行计算，进一步计算支撑区受压区比例。计算结果如图12 所示，圆心角 ω 取180°～230°时，受压区占整个支撑区的比例约32%～34%。由式（14）计算得到，切口圆心角超过190°时，失稳系数接近满足＞1.5 的要求（见图13）。而该工程爆破方案确定的切口圆心角为220°，失稳系数=2.53，说明切口圆心角偏大，倾覆力矩远大于抵抗力矩，一旦切口角部混凝土失效，受压区必然向受拉区快速扩展，很难避免下坐现象的出现。

图12 切口圆心角 ω 与支撑区受压占支撑区比例ζ 的关系Fig. 12 Relationship between the blasting notch’s central angle and the compressive region ratio

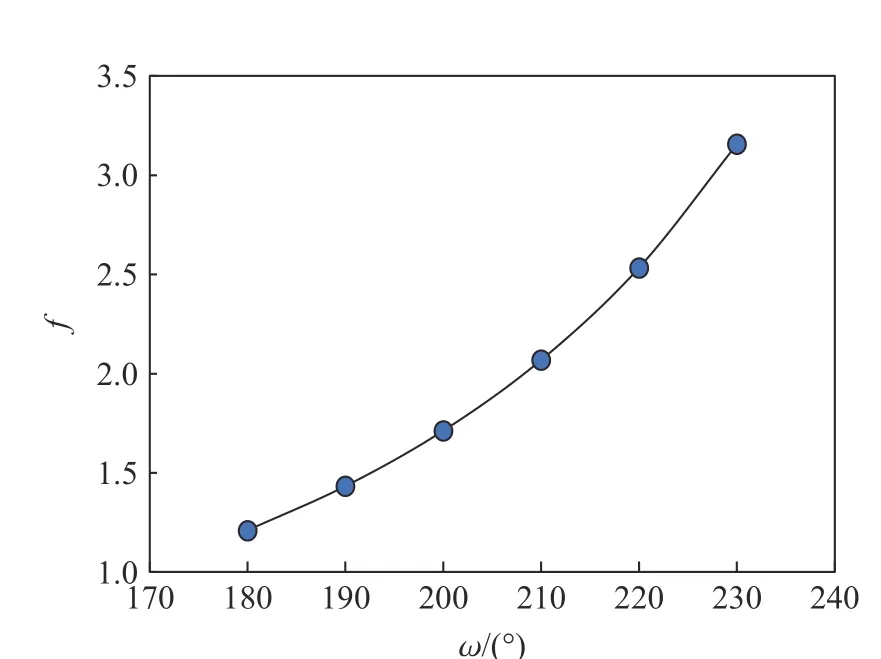
图13 切口圆心角 ω 与烟囱倾覆失稳系数f 的关系Fig. 13 Relationship between the blasting notch’s central angle and the instability coefficient

4.2 下坐判别

已知烟囱自重，根据爆破切口形状取支撑区下部的最小截面面积=10.07 m，上部最大截面面积=33.56 m，取混凝土残余强度σ=0.2σ=5.36 MPa 时，得到：

计算结果表明，该工程原设计方案将发生下坐现象，且支撑区横截面面积较小的下半部分的破坏将导致烟囱加速下坐，而横截面面积较大的上半部分则使下坐减速，但当减速产生的加速度超过-9.8 m/s时，下段支撑区也将承受大于2的荷载，整个支撑区可能完全被压溃，此时爆破切口将因下坐而完全闭合，倾覆力矩也将消失，烟囱存在“炸而不倒”的风险。因此，预测结果与烟囱实际下坐情况基本吻合。

4.3 下坐诱发空中断裂的判别

设烟囱自重与支撑区残余承载力相等时，对应的支撑区横截面面积为28.58 m，截面距离切口底边1.44 m，切口总高度5 m，则可能发生加速下坐的高度为2.96 m，近似取3 m 进行计算时，由式（28）计算得到加速下坐可能获得的最大初速度≈7.67 m/s。分别取η=1，1.5，由式(31) 计算得到烟囱下坐由7.67 m/s 减速至0 时所需的时间区间为：

计算结果表明（见图14），在烟囱下坐结束阶段，若其历时较短（如=0.06 s），随着烟囱横截面所处高度的增加，其竖向（烟囱轴向）峰值应变呈现出先增大后减小的趋势，呈现出“应变高程放大效应”。而若下坐结束历时较长（如=0.15 s），则“应变高程放大效应”消失，此时随着高度的增加，应变持续减小。

图14 减速过程对轴向应变放大系数ξ 的影响Fig. 14 Distribution of amplification factor of longitudinal strain in deceleration process

定义烟囱某处横截面与底部冲击断面上轴向峰值应变的比值为该处动应变放大系数ξ，下坐结束阶段历时较短时，峰值应变出现的相对位置较高，例如=0.06 s 时ξ 最大值出现在约90 m高度处，=0.1 s 时ξ 最大值出现在约60 m 高度处。

因此，当=0.06～0.1 s 时，存在ξ＞1 的可能，发生空中压溃的概率较高（忽略动应变衰减情况下）。本试验中180 m 烟囱空中折断位置大约位于距底端90 m 处，与=0.06 s 的情况较吻合。

4.4 讨论

由上述180 m 高烟囱下坐诱发空中断裂的案例可知，下坐产生的冲击荷载可造成烟囱的损伤甚至断裂。为了分析其他常见钢筋混凝土烟囱的断裂风险，对5 种典型烟囱进行了分析。假定烟囱下坐碰撞基础的最大速度为3 m/s，经历0.06 s 后速度降为0。忽略附加动应变沿烟囱轴线逐渐衰减时，计算结果（见表2）表明，随着烟囱高度的增加，烟囱的最大动应变放大系数ξ 由1.093 增加到1.728。烟囱越高，动应变放大系数越大，发生断裂的风险也越大。并且随着烟囱高度的增加，烟囱最大动应变放大系数所处的相对高度也随之增加，由烟囱中下部提升至烟囱中上部。实际上，当考虑附加动应变随传播距离发生衰减时，高烟囱发生空中断裂的可能性较高，而矮烟囱发生空中断裂的可能性较低。

表2 不同高度烟囱的最大动应变放大系数Table 2 Maximum amplification factor of peak dynamic strain of chimneys with different heights

由上述分析可知，避免烟囱下坐或者避免硬着陆是预防烟囱早期空中断裂的重要措施，具体可采用以下方法：

(1) 优化爆破切口形状，改梯形切口为三角形切口或喇叭形切口，使支撑区截面面积逐渐过渡至整个圆环截面，增大支撑区的极限承载力，避免支撑区被瞬间整体压溃；

(2) 优化爆破切口的圆心角，在满足倾覆条件时，需考虑支撑区的残余承载力，通过增大支撑区截面面积减小下坐的速度；

(3) 必要时应对支撑区混凝土进行加固，提高其抗压强度。

5 结 论

高烟囱爆破拆除过程中，常出现下坐和中部断裂的现象，严重影响爆破安全和爆破效果。结合典型钢筋混凝土烟囱爆破拆除工程，分析了烟囱下坐和空中断裂的宏观特征，并研究了其力学机制，构建了判别力学模型，得到以下结论。

(1) 传统的烟囱爆破设计方法认为，支撑区轴心受压极限承载力大于烟囱的重量即可预防支撑区的压溃，然而支撑区实际处于大偏心受压状态，因此，正截面轴心受压稳定条件不能作为下坐判别条件。

(2) 爆破切口形成后，基于混凝土的全应力-应变曲线特征以及应力和应变在支撑区横截面的分布特征、倾覆力矩与抵抗力矩的比值应作为切口设计的控制条件之一；且＞2 时支撑区受压截面面积过小可能使其发生强烈压缩破坏而导致烟囱下坐。

(3) 大偏心受压作用下支撑区混凝土的压缩破坏不可避免，支撑区最小残余承载力小于烟囱的重量是下坐判别的必要条件。

(4) 高度超过100 m 的混凝土烟囱在下坐结束阶段，其底端与基础碰撞产生冲击荷载作用，在烟囱中部诱发的应变值可能大于其底端的失效应变，即诱发动应变高程放大效应，该现象是导致烟囱发生早期断裂的主要原因。

(5) 烟囱越高，下坐冲击历时越短，动应变高程放大效应越显著，发生断裂的风险也越大。随着烟囱高度的增大，烟囱最大动应变放大系数所处的相对位置也随之变化，将由烟囱中下部移至烟囱中上部。