12.7 mm 弹侵彻不同强度钢靶的数值模拟*

王凯雷，李明净，董雷霆

（北京航空航天大学航空科学与工程学院，北京 100191）

对穿甲侵彻问题的研究方法主要有实验、理论分析和数值模拟。实验结果可靠性最高，能够为理论分析和数值模拟提供参照标准。然而，实验研究成本高、准备实验材料等耗时长，且只能得到少量数据点。理论分析便于更深刻地理解侵彻原理，通过理论公式能够快速建立多种变量之间的关系。但是，理论分析需要理想化的假设，对模型进行大量简化，对于涉及弹靶同时失效的复杂问题，理论分析难以实现。通过数值求解能够完整再现整个侵彻过程，可以获取实验中难以得到的数据。随着计算机水平不断提高，数值模拟已成为研究穿甲侵彻问题的重要手段之一。

对于子弹侵彻装甲钢的数值模拟，根据子弹的破碎情况可分为2 类。一类是子弹强度相比于靶板强度较高，子弹侵彻金属靶板之后几乎没有变形或损伤。数值模拟中，通常将子弹视为刚体，比如Dey 等和Flores-Johnson 等在实验中观察到子弹形貌始终保持完整，因此在数值模拟时将子弹设置为刚体。随着钢材料的不断发展，靶板材料的力学性能不断提升，不少超高强钢的强度可以达到2 GPa 以上。而实际弹体多由硬质合金钢制成，其屈服强度约为1.6 GPa。当子弹撞击超高强靶板时，子弹可能会发生破碎现象。因此，另一类考虑子弹破碎的数值模拟得到越来越多的关注。例如：赵太勇等开展了12.7 mm 动能弹冲击装甲钢的实验，结果表明弹体的破坏模式以断裂侵蚀为主，数值模拟再现了弹体的破碎过程。Chen 等、陈刚等和Chen 等在钝头弹侵彻钢靶实验中发现弹头呈向日葵形的破坏形式，数值模拟结果与实验基本一致。Fras 等模拟了7.62 mm 弹撞击带孔板时的破碎情况。Paris等模拟了钢弹侵彻钢靶的过程，采用最大主拉应力层裂失效模型，预测了子弹破碎情况，并与实验结果进行了对比。石益建等采用数值方法模拟了12.7 mm 穿甲弹侵彻异形BC/Al 复合靶板，结果表明异形陶瓷靶板更易使弹丸变形破碎。其他的相关工作可参见Woodward 等、谢恒等和Borvik 等的研究。

对于弹靶侵彻的数值模拟已进行了大量研究，但多数模拟只针对子弹保持完整的情况，或者只模拟子弹破碎的情况，很少使用同一模型来模拟这2 种情况。而魏刚在同时模拟这2 种情况时发现，适用于子弹破碎的数值模型无法模拟子弹保持完整的情况，弹头总会发生侵蚀现象。由此可见，目前有关弹靶侵彻的数值模拟存在明显的局限性，仅能模拟单一模式的子弹侵彻行为。

为此，本文中拟建立一种通用的弹靶模型，既可以用于模拟子弹侵彻低强度钢靶保持完整的情形，也适用于子弹侵彻超高强度钢靶发生破碎的情况，将来可用于研究子弹发生破碎条件、靶板结构设计等问题。

1 实验和数值模拟方法

基于12.7 mm 穿甲弹侵彻60 mm 厚603 钢靶板标准穿深实验，利用LS-DYNA 软件建立相应的三维数值模型进行模拟。

1.1 实验方法和结果

采用12.7 mm 穿甲弹垂直侵彻60 mm 厚的603 钢靶，实验重复3 次。实验后用游标卡尺测量侵彻深度，并对靶板进行剖分，查看弹坑形状。图1 为12.7 mm 穿甲弹弹芯和弹坑的剖面。12.7 mm 弹芯由硬质合金钢制成，质量约为30 g，长度为51.6 mm，弹芯直径为10.8 mm。3 次实验的弹丸初始侵彻速度分别为810、819 和818 m/s，穿深分别为29.5、30.1 和30.5 mm，平均穿深为30.0 mm。

图1 弹、靶实物Fig. 1 The projectile and target

1.2 数值模型

根据实验，建立如图2 所示的数值模型。考虑到问题的对称性，仅建立1/4 对称模型。靶板周围及底面采用固定约束，对称面采用对称约束。子弹采用有限元方法（finite element method, FEM）的Lagrange 算法，靶板中心区采用光滑粒子流体动力学（smooth particle hydrodynamics, SPH）算法，周围区域采用FEM 的Lagrange 算法。数值模拟中，子弹的初始侵彻速度设置为820 m/s。

图2 数值模型Fig. 2 The numerical model

2 材料模型及参数验证

子弹和靶板采用Johnson-Cook 材料模型，该模型是目前在冲击侵彻问题中应用最广泛的本构模型之一。Johnson-Cook 模型可以较好地描述金属材料在高应变、高应变率、高温条件下的力学行为，其表达式为：

本文中603 钢的材料参数通过霍普金森杆动态实验曲线获得。Johnson-Cook 模型中的材料参数、、可以根据室温、某恒定应变率下的应力-应变曲线拟合获得，图3 为1 842 s应变率下材料参数、、的拟合曲线与实验结果的对比。对于参数，大部分钢类材料的温度敏感系数均在1.0 附近，因此，本文中603 钢的取1.0。

图3 603 钢参数拟合Fig. 3 Parameter fitting of 603 steel

标定材料参数时，通常的做法是通过霍普金森杆实验测定一系列恒温条件下不同应变率的应力-应变曲线，然后取恒定应变时的应力值，作出 σ /(+ε)-1 和 l n(ε˙/ε˙) 的关系曲线，根据该曲线标定。然而，霍普金森杆实验应变率约在10s量级，而在弹靶侵彻过程中，材料的应变率一般在10s量级以上。显然，采用在较低应变率下获得的实验数据拟合的参数是否适用于高速冲击问题还有待验证。本文中根据标准穿深实验，采用图2 所示的弹靶模型，对参数进行了一系列反演计算。根据实验现象，在数值模拟中将子弹视为刚体。图4 为实验结果与数值模拟结果的对比。实验平均穿深为30.0 mm，数值模拟的穿深为32.9 mm，相对误差约为9.7%。而且，靶板表面的弹坑附近隆起高度也基本一致。由此可见，本文中采用的603 钢材料参数在模拟12.7 mm 弹高速侵彻方面是比较准确的。

图4 12.7 mm 穿甲弹侵彻半无限厚603 钢板实验与模拟结果对比Fig. 4 Comparison between experiment and numerical simulation of 12.7-mm projectiles penetrating semi-infinite 603 steel targets

由于子弹材料参数直接影响其在侵彻过程中的变形和破坏，因此在模拟子弹破碎时，需要谨慎采用合理的材料参数。表1 中弹芯的材料参数来源于文献[6]，绘制弹芯材料在1 和10s应变率下的应力-应变曲线，如图5 所示。图5 中，当应变率为10s时，若按照=0.075，可以看到子弹的等效应力达到了6 000 MPa 以上。为了考察子弹材料参数的合理性，根据文献[18]，绘制了不同金属材料在应变率为10s时，1 +ln(ε˙/ε˙) 与的关系曲线，如图6 所示。1+ln(ε˙/ε˙)表示材料取相同等效应变时，高应变率下的等效应力相比于参考应变率下等效应力的提高倍数。从图6 可以看到，对大部分金属材料而言，在10s应变率下，等效应力的提高倍数在1.5 以下。目前已知的超高强钢材料在准静态下的屈服强度达到1 900 MPa，在10s应变率下，该材料的等效应力按照1.5 倍提高，也仅为2 850 MPa，远低于子弹的等效应力6 000 MPa。由此可见，子弹的材料参数=0.075 是偏大的。因此，本文计算中适当调低子弹的材料参数至0.007 5，调整后子弹在10s应变率下的应力-应变曲线见图5。

表1 12.7 mm 穿甲弹弹芯和靶板的材料参数Table 1 The material parameters for the 12.7-mm-diameter armor-piercing projectiles and targets

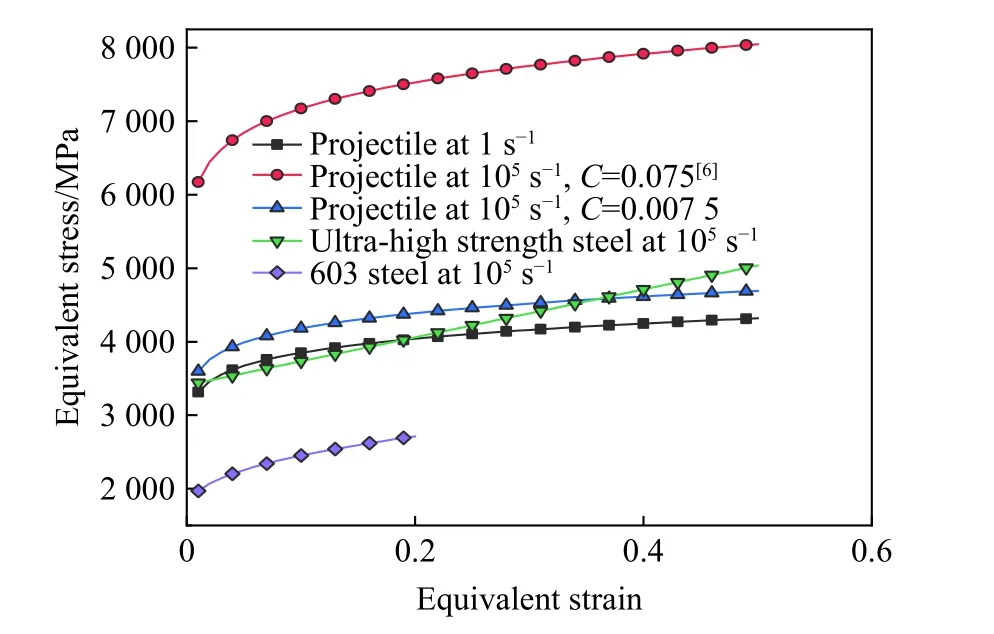
图5 子弹材料与603 钢和超高强钢的应力-应变曲线对比Fig. 5 Comparison of stress-strain curves of projectile material with those of 603 steel and ultra-high strength steel

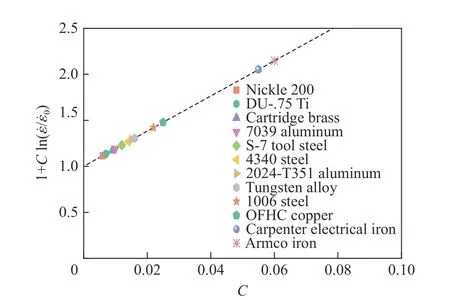
图6 不同金属材料的 1 +C ln(ε˙/ε˙0) 与C 的关系[18]Fig. 6 Relations of 1 +C ln(ε˙/ε˙0) and C for different metals[18]

考虑到本文的一个目的是，模拟子弹在侵彻强度较高的金属靶板时子弹产生破碎的情况；如果超高强钢的强度相比于子弹的强度过低，子弹在侵彻超高强钢靶板的过程中很可能不会发生破坏。因此，在设置超高强钢材料参数时，适当提高了材料强度，使10s高应变率下超高强钢的应力-应变曲线与子弹的大致相当。参考603 钢的材料参数，高强钢的参考应变率取整设置为2 000 s，屈服强度取2 850 MPa。参数和共同决定了材料的应变硬化效果，这里取=1，使材料的应变硬化程度仅由参数决定。从图5 可以看出，即使超高强钢的屈服强度取2 850 MPa，相比于子弹仍然较弱。因此，在对超高强钢参数取值时，适当增大了的值。子弹的应变硬化斜率约为1 000 MPa，超高强钢取=5 000 MPa。超高强钢材料参数和均参考603 钢的设置，分别取=0.05 和=1。尽管超高强钢材料参数采用了较高的估计值，但从图5 可以看出超高强钢的强度仍然略低于子弹的强度，也说明文献[6]中子弹的参数偏高。

3 子弹侵彻均质603 钢靶

基于12.7 mm 子弹侵彻603 钢的实验，研究子弹和靶板应当采用何种模型算法。在确定算法后，进一步研究了网格尺寸对计算结果的影响，并建立了一种可用于预测子弹破碎的弹靶数值模型。实验中603 钢靶的厚度为60 mm，本节中为了降低计算量，将靶板计算模型的厚度进行了适当减小，所有的模型尺寸均为75 mm×75 mm×40 mm。

3.1 靶板算法选择

靶板一般采用FEM 网格建模，但在弹靶侵彻过程中，靶板具有较大的变形，这会引起网格较大的变形，严重时甚至产生畸变，导致计算无法进行。为了使计算能够进行，通常会设置网格侵蚀参数，当网格变形到一定程度时，网格自动删除。然而，网格删除是一种数值处理手段，会造成材料丢失，并不符合物理过程。在12.7 mm 子弹侵彻603 钢靶板的剖面图（见图4）中可以看出，靶板受到子弹的强烈挤压作用，是典型的延性扩孔失效模式，并没有材料丢失。

SPH 方法是一种无网格方法，可以模拟材料较大的变形，不需要进行网格删除。为了比较这2 种算法对计算结果的影响，本文中分别建立了FEM 和SPH 算法的靶板模型。由于实验中未观察到子弹发生明显变形，因此对子弹采用刚体材料模型。

FEM 靶板模型如图7(a) 所示，冲击区域网格尺寸为0.15 mm，周边区域采用较粗的网格，共约290 万个网格。子弹与靶板之间采用CONTACT_ERODING_SURFACE_TO_SURFACE 侵蚀算法。

SPH/FEM 靶板模型如图7(b)所示，由于SPH 算法会引起计算量显著增加，因此仅在冲击区域设置SPH 粒子，粒子间距为0.15 mm，在非冲击区域采用FEM 网格，共约164 万个SPH 粒子和128 万个FEM 网格。SPH 粒子与FEM 网格采用CONTACT_TIED_NODES_TO_SURFACE_OFFSET 方式连接。子弹与靶板之间采用CONTACT_ERODING_NODES_TO_SURFACE 侵蚀接触算法。

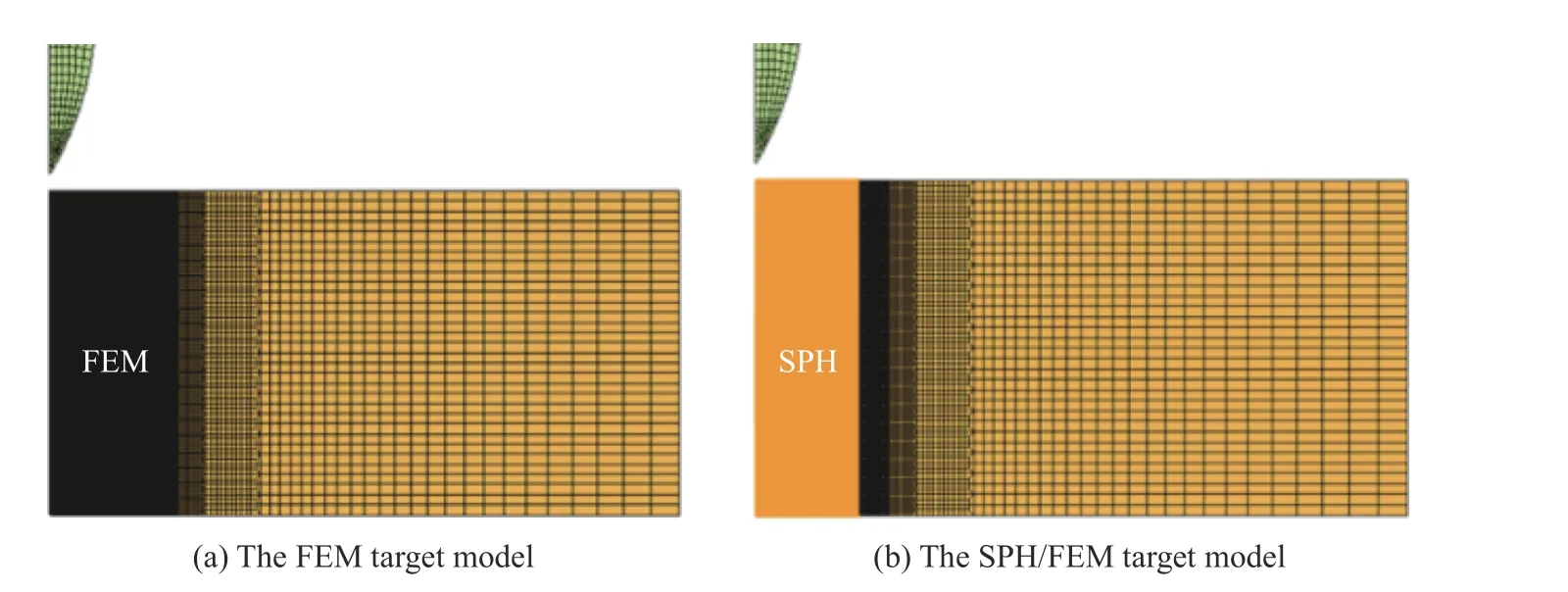
图7 采用不同算法建立的靶板模型Fig. 7 The target models with different algorithms

在FEM 靶板模型中，需要设置网格侵蚀的失效参数，否则会出现如图8 所示的子弹与靶板相互穿透的现象。

将等效塑性应变 ε作为失效准则，对靶板设置了多组失效应变值进行比较，来考察这2 种算法计算结果的准确性。图9 为设置不同 ε值时，FEM 靶板模型和SPH/FEM 靶板模型的侵彻深度计算结果。从图9 可以看出，采用FEM 靶板模型计算得到的侵彻深度总是大于采用SPH/FEM 模型的计算结果。采用FEM 靶板模型计算得到的的侵彻深度会随着 ε的增大而减小，而采用SPH/FEM 模型计算得到的侵彻深度基本是不变的。主要原因是：FEM 靶板模型计算中采用了网格侵蚀，但删除单元会使一部分材料丢失，从而使靶板对子弹的阻碍作用减弱，计算穿深会大于实际穿深；而SPH/FEM 靶板模型的粒子在计算过程中并没有消失，始终对子弹有阻碍作用，计算结果更加接近实验值。因此，若将子弹视为刚体，SPH/FEM 靶板模型的计算结果与实验结果吻合更好。另外，当 ε设置过大时，如 ε≥2.3，FEM 靶板模型计算时也会出现图8 中弹靶网格相互穿透的现象。而SPH/FEM 模型中， ε可以设置得很大，不会引起计算错误。

图8 弹靶网格相互穿透Fig. 8 Penetration of the projectile and target grids into each other

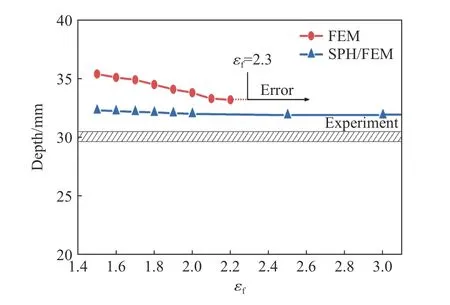
图9 不同失效应变下，FEM 靶板模型与SPH/FEM 靶板模型计算得到的侵彻深度的对比Fig. 9 Comparison of penetration depths obtained by the FEM target model and the SPH/FEM target model at different given failure strains

3.2 子弹算法

将子弹考虑为可变形体，具体材料参数见表1。子弹分别采用FEM 和SPH 算法建立模型，见图10。靶板也有FEM 和SPH 等2 种建模方式，共4 种弹靶模型：模型1，FEM 子弹-FEM 靶板；模型2，FEM 子弹-SPH 靶板；模型3，SPH 子弹-FEM 靶板；模型4，SPH 子弹-SPH 靶板。这4 种模型中，靶板材料均为603 钢。

图10 采用不同算法建立的子弹模型Fig. 10 The projectile models with different algorithms

模型1 和模型2 与3.1 节中的计算模型完全一致，仅更改了子弹的材料模型。为了保证子弹在发生变形时，计算能够进行，设置子弹侵蚀准则为失效应变为0.2，与文献[8]中给出的弹丸失效应变0.17 接近。子弹网格尺寸约为0.8 mm，共计1 377 个FEM 网格。

模型3 和模型4 的子弹采用SPH 算法。由于模型3 中子弹SPH 粒子与靶板FEM 网格之间需设置CONTACT_ERODING_NODES_TO_SURFACE 侵蚀接触算法，较大的SPH 粒子间距会导致粒子与网格之间发生穿透；因此，在模型3 中，将子弹SPH 粒子间距调整为0.4 mm，靶板FEM 网格尺寸调整为0.25 mm。对模型4，子弹的SPH 粒子间距与模型3 的保持一致，靶板的SPH 粒子间距调整为0.25 mm。

4 种模型的计算结果如图11 所示。由图11 可以看出，在采用相同的材料参数情况下，不同的建模方式得到的计算结果差异很大。而且，仅有模型2 的计算结果与实验结果吻合，即子弹保持完整形态。模型1、3、4 的计算结果中，子弹头部均发生了严重的变形和侵蚀现象，这与实验现象不符。

图11 不同弹靶模型的计算结果Fig. 11 Numerical results obtained by different projectile-target models

图12 为图11 对应模型在不同时刻的弹头局部放大图。从图12(a)可以看到，模型1 中，子弹头部在侵彻过程中发生了一定的变形。随着侵彻过程的进行，子弹头部变形程度不断提高，直到弹头变形达到设置的单元删除准则，导致弹头单元被删除。图13 为模型1 弹头局部放大图，可以看出弹头部分发生了沙漏变形，这可能是导致弹头发生变形的原因。

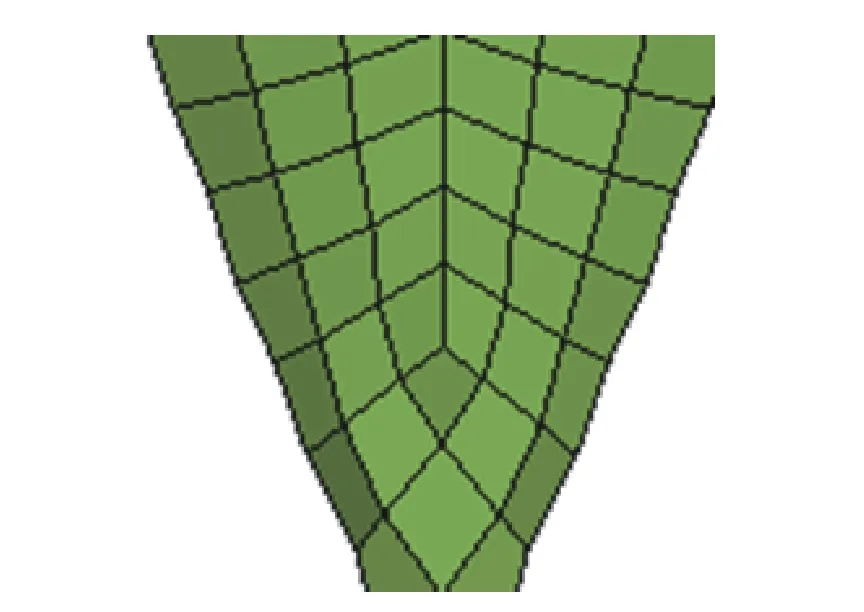
图13 模型1 弹头局部放大Fig. 13 Partial amplification of the projectile nose for model 1

图12(b)为模型2 弹头的侵彻过程，子弹在侵彻过程中基本没有变形，始终保持初始形状。

图12(c)和图12(d)分别为SPH 子弹对FEM 靶板和SPH 靶板的侵彻过程。当子弹采用SPH 算法建模后，子弹在接触到靶板时，头部即产生了明显的变形。

图12 不同弹靶模型的侵彻过程Fig. 12 The penetration processes obtained by different projectile-target models

因此，采用SPH 算法建立的子弹模型，难以模拟这类子弹变形很小的侵彻过程。而采用FEM 方式建立子弹模型后，靶板的建模方式对计算结果也有显著影响。FEM 靶板与FEM 子弹接触时，会使子弹产生异常的沙漏变形。综上所述，FEM 子弹-SPH 靶板（模型2）能够较好地模拟12.7 mm 弹侵彻603 钢靶板的实验现象，见图12(b)。

3.3 网格尺寸的影响

为了进一步考察模型2 的可靠性，开展了网格尺寸对计算结果的影响研究。在本文中，不仅需要确定子弹的FEM 网格尺寸和靶板的SPH 粒子间距，还需要考虑FEM 网格和SPH 粒子大小的匹配问题。对于子弹的网格划分，设置了2 种方案：一种是弹体半径方向有6 个单元，网格尺寸约为0.8 mm；另一种是弹体半径方向有12 个单元，网格尺寸约为0.4 mm。同时，设置了3 组不同的子弹FEM 网格尺寸和靶板SPH 粒子间距比，分别为3.2、4.0、5.3，共计6 组算例。具体的子弹FEM 网格尺寸/靶板SPH 粒子间距分别为0.8 mm/0.25 mm、0.8 mm/0.20 mm、0.8 mm/0.15 mm、0.4 mm/0.125 mm、0.4 mm/0.10 mm 和0.4 mm/0.075 mm，模拟结果如图14 所示。

从图14 可以看出，子弹FEM 网格尺寸和靶板SPH 粒子间距之比对计算结果影响明显。当子弹FEM 网格尺寸和靶板SPH 粒子间距之比为3.2 或4.0 时，靶板SPH 粒子与子弹FEM 网格接触也会使子弹网格产生沙漏变形，如图14(a)～(b)、(d)～(e)所示。这与3.2 节中模型1 的计算结果类似，见图12(a)和图13。而当子弹FEM 网格尺寸和靶板SPH 粒子间距之比增大至5.3 时，子弹网格沙漏变形消除，如图14(c)和(f)所示。弹靶0.8 mm/0.15 mm 算例（见图14(c)）和弹靶0.4 mm/0.075 mm 算例（见图14(f)）的模拟情况基本一致，然而，弹靶0.4 mm/0.075 mm 算例的网格和粒子数量会大幅度增加，计算效率大幅度下降，计算所需内存也会大幅度增加。综上，为防止子弹头部出现沙漏变形，子弹FEM 网格尺寸和靶板SPH 粒子间距之比可以设置在5.3 左右，可采用子弹FEM 网格尺寸0.8 mm/靶板SPH 粒子间距0.15 mm的设置。

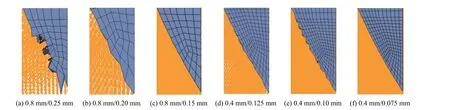
图14 不同的子弹FEM 网格尺寸和靶板SPH 粒子间距组合下的计算结果Fig. 14 Numerical results for different combinations of projectile FEM mesh size and target SPH particle spacing

4 子弹侵彻超高强钢靶板

在确定模型算法及网格尺寸，并与实验结果对比验证后，进一步开展12.7 mm 弹侵彻超高强钢的数值模拟。计算模型与3.3 节中子弹0.8 mm/靶板0.15 mm 模型设置完全一致，仅将靶板材料更改为超高强钢，超高强钢材料参数见表1。计算结果如图15 所示。

图15 粗糙网格子弹对超高强钢靶的侵彻过程Fig. 15 Penetration process of the projectile with coarse mesh into the ultra-high strength steel target

从图15 可以看出，子弹在侵彻超高强钢靶的初期（=6 µs），弹头受到靶板挤压，发生了一定的变形。在=8 µs 时，由于应变超过了所设置的失效值，弹头被破坏。随着侵彻过程的进行，弹头部分不断遭到破坏。数值模拟在进行到=38 µs 时，计算报错，原因是子弹网格过于粗糙，单元删除后粒子与网格之间的接触算法不稳定。因此，重新建立了网格尺寸约为0.4 mm 的子弹模型，并进行计算，计算结果如图16 所示。

图16 细化网格子弹对超高强钢靶的侵彻过程Fig. 16 Penetration process of the projectile with refined mesh into the ultra-high strength steel target

细化子弹网格后，计算可以一直进行到=56 µs，此时子弹速度降至零。与子弹网格尺寸为0.8 mm的模型的计算结果相比，在=0～34 µs 时间段内，弹头的破坏情况基本一致。

魏刚对卵形弹侵彻金属靶板的破坏行为进行了详细的实验与讨论。由于本文模拟中采用的子弹、靶板与魏刚实验中的具有一定的相似性，如表2 所示，因此将本文的模拟结果与魏刚实验中的子弹破坏形式进行了比较。魏刚对弹靶采用了不同的材料，但这2 种材料的性能比较接近，其中弹体材料屈服强度为1 614 MPa。本文中的弹体屈服强度为1 580 MPa，尽管本文靶板材料的屈服强度为1 900 MPa，高于子弹的，但是从图4 可以看出，在10s高应变率下，靶板材料的动态性能与子弹的是相近的。因此，本文中模拟的子弹侵彻超高强钢靶的算例也是2 种性能相近的钢发生侵彻。与此同时，本文中也根据魏刚的弹靶模型进行了数值模拟，并与其中的实验结果进行了比较。

表2 本文与文献[8]的弹靶比较Table 2 Comparison of the projectile and target used in this study with those used in Reference [8]

图17 展示了魏刚的实验和模拟结果及本文的模拟结果。在魏刚的实验中，当子弹撞击速度从573.0 m/s 升高到883.5 m/s 时，子弹均发生了头部破碎的现象，且弹尾部分直径未发生明显变化。从图17 可以看出，魏刚的模拟结果弹体头部发生了部分侵蚀，但与实验现象存在一定的差异，而本文的弹头破坏行为与实验现象基本一致。图17 同时列出了实验和模拟获得的残余弹体的长度。实验结果表明，在不同撞击速度下，残余弹体的长度基本一致。本文的模拟结果和魏刚的模拟结果均反映了这一规律。文献[8]和本文残余弹体长度的模拟结果均比实验值偏高，绝大部分结果的相对误差在20%～29%之间，绝对误差在3～8 mm 之间。总体来看，模拟结果还是比较有效的。本文中采用12.7 mm弹侵彻超高强钢靶的模拟中，残余弹体长度的模拟结果约为26.0 mm，而魏刚的残余弹体长度实验结果为27.4～29.0 mm。通过与魏刚的实验结果对比，可以验证本文的模拟结果具有一定的有效性。

图17 模拟结果与相关实验结果的对比Fig. 17 Comparison between the simulation and the related experimental results

虽然本节中通过细化网格成功地模拟了子弹侵彻超高强钢靶时，弹头发生破碎的现象，但是3.3 节中的计算结果表明，子弹网格尺寸为0.4 mm 和靶板粒子间距为0.125 mm 的模型无法模拟子弹不破坏的侵彻过程，见图14(d)。综上所述，粗糙网格（网格尺寸为0.8 mm）的子弹模型可以模拟子弹不破坏的侵彻过程，并且可以初步预测子弹是否会发生破坏，但无法模拟子弹破坏的完整侵彻过程。为了获得完整的侵彻过程，还需要进一步建立细化网格的子弹模型。

5 FEM/SPH 耦合弹靶数值模型及模拟结果

尽管3.4 节中的方法能够初步预测子弹破碎和模拟完整侵彻过程，但需要分别建立粗糙网格的子弹模型和细化网格的子弹模型。本文中希望建立一个通用的数值模型，在仅改变靶板材料的情况下，即可模拟子弹保持完整或破碎的侵彻过程。通过观察之前的模拟结果，可以发现子弹网格尺寸是影响计算结果的关键因素。在子弹未破碎的情况下，主要是子弹表面网格与靶板粒子接触。而在子弹发生破碎后，主要是子弹内部网格与靶板粒子接触。根据这一特点，建立了表面网格相对粗糙、内部网格较细的子弹模型，如图18所示。子弹表面网格尺寸约为0.8 mm，内部网格的尺寸约为0.3 mm，粗网格与细网格之间采用过渡网格。

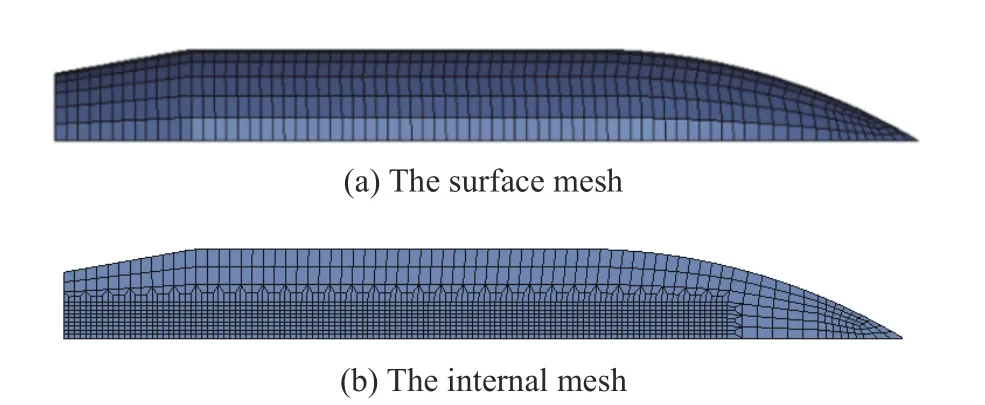
图18 改进网格形式的三维子弹模型的改进网格形式Fig. 18 The improved mesh forms of the three-dimensional projectile model

采用通用的弹靶数值模型分别模拟12.7 mm 弹侵彻603 钢靶和超高强钢靶，弹靶侵彻模拟结果见图19。图19(a)为子弹侵彻603 钢靶板的过程，由于603 钢强度相比于子弹较弱，子弹几乎不变形，与实验结果基本一致，见图1。图20(a)为子弹侵彻603 钢靶板情况下，子弹表面与内部某单元的等效塑性应变时间历程。表面单元最大等效塑性应变为0.001 3，内部单元最大等效应变为0.011。而对于子弹侵彻超高强钢靶的过程，如图19(b)所示，由于靶板强度较高，子弹头部会产生比较明显的变形，当变形达到设置的失效值后，单元被删除，即弹头遭到侵蚀破坏。改进模型的计算结果与图16 和图17(a)的模拟结果基本一致，与魏刚的实验结果也具有一定的相似性。图20(b)展示了子弹侵彻超高强钢靶情况下，弹头表面与内部某单元达到等效塑性应变为0.2 后即被删除。

图19 改进网格模型的弹靶侵彻过程模拟结果Fig. 19 Projectile-into-target penetration processes simulated by the improved mesh model

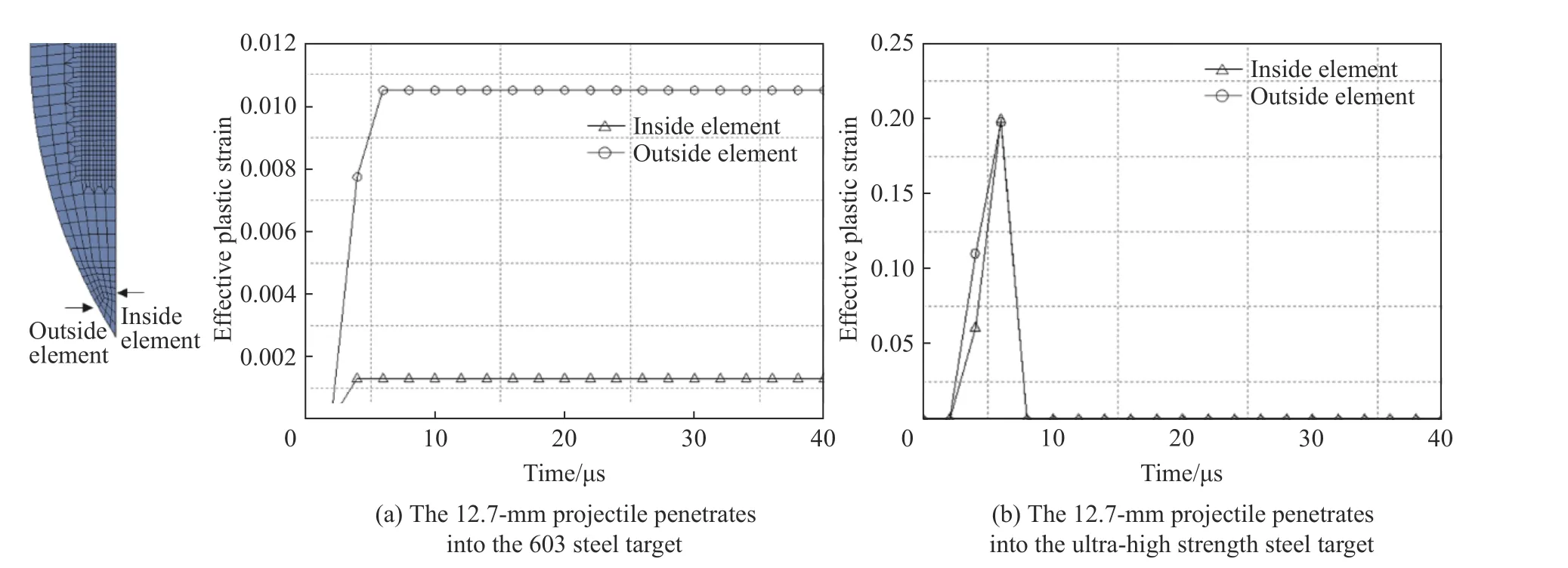
图20 子弹内部单元和外部单元的等效塑性应变时间历程Fig. 20 Effective plastic strain-time curves of the inside and outside elements of the projectiles

这里弹体失效准则并不是真实的失效准则，仅表示弹体变形到达一定程度后弹体破碎。考虑到弹体一般由硬质合金钢制成，延性较差，因此在子弹侵彻超高强钢的真实情况下，弹体可能更容易发生侵蚀破坏。本文的研究目的仅用于验证模型是否能够模拟弹体破碎的情况，更准确的弹体破碎模拟可以采用Johnson-Cook、C-L 等断裂准则，具体可参考Johnson 等、 Chen 等、Børvik 等和Xiao 等的研究。

本文算例在Intel(R) Core(TM) i7-6 700 3.4GHz 四核处理器上进行，改进模型的计算时间约为12 h，整体细化网格模型的计算时间约为18 h。相比较而言，改进模型的计算时间缩短了近30%。

6 结 论

针对12.7 mm 弹侵彻不同强度金属靶板，结合603 钢穿深实验，在深入研究模型算法、网格尺寸的基础上，分别模拟了子弹保持完整和产生破碎2 种情况，得到以下结论。

(1) 12.7 mm 弹侵彻603 钢靶的实验中，子弹保持完整形态。模拟中，弹靶模型算法对计算结果影响极大。子弹和靶板分别采用FEM 算法和SPH 算法建模后，计算结果与实验基本一致。

(2)子弹FEM 网格尺寸与靶板SPH 粒子间距的比例对计算结果有显著影响，该比例需要保持在5.3 附近或以上。若小于该比例，会出现与实验现象不符的网格畸变模拟结果。

(3)在模拟子弹破碎时，弹靶尺寸比例为5.3 的情况下，粗糙网格删除会引起计算中止。细化子弹网格可有效避免该问题，并且能够较好地模拟子弹破碎现象，模拟结果与实验一致，但该网格尺寸比例不适合模拟子弹在侵彻中保持完整的情况。

(4)为了能够采用同一个模型模拟子弹保持完整或产生破碎的情况，可以建立表面粗网格、内部细网格的FEM 子弹模型，采用SPH/FEM 耦合算法建立靶板模型，从而避免网格畸变和计算中止问题。