地面和埋置爆炸土中地冲击作用分区数值模拟及试验研究*

刘 琦，翟超辰，张跃飞，曲建波，吴祥云

（1. 湘潭大学土木工程与力学学院，湖南 湘潭 411105；2. 军事科学院国防工程研究院工程防护研究所，河南 洛阳 471023）

地表或浅埋爆炸产生的能量一方面用于破碎爆炸附近的岩土介质形成飞散的抛掷体，另一方面与地表上面的空气发生相互作用，在空气中形成冲击波。爆炸时，通过直接压缩地介质并在其中形成的波称为直接地冲击，而空气中的冲击波掠过地表，通过压缩空气和地介质相互作用形成的在地介质中传播的波称为感生地冲击。所以爆心附近土中浅层地下介质所受地冲击荷载比较复杂，既有直接地冲击，也有感生地冲击。地冲击和空气冲击波到达地表观测点的时间相对关系由岩土介质中的地冲击传播速度和空气冲击波传播速度差异决定，不同介质、不同埋置深度的爆炸造成地冲击应力、加速度场的不同分布。

近年来，对于岩土介质中直接地冲击方面的研究已经较为完善。Wu 等通过现场大型地下爆炸试验，研究了介质内部、岩土界面和地表的爆炸应力波特性；给出并分析了实测应力波时程及其特征参数，如质点速度峰值和质点加速度峰值以及不同位置的主频率。何翔等通过石灰岩中不同装药深度的爆炸试验，得到了石灰岩中爆炸成坑经验公式以及地冲击传播规律。Leong 等根据新加坡残积土的小规模现场爆破试验，检验了TM5-855-1 对应力峰值的估算。吴祥云等通过现场试验研究了常规装药爆炸埋深对自由场直接地冲击参数的影响，得到了不同岩土介质、不同地冲击参数等效当量埋深系数的计算方法。叶亚齐等运用等效当量埋深系数，给出了砂质黏土中不同深度爆炸自由场地冲击参数的预估方法。Yankelevsky 等通过现有经验数据的分析和数值模拟，研究了土中爆炸冲击波峰值压力衰减特性。Jayasinghe 等对不同埋深爆炸条件下饱和砂土中桩的动力响应进行了数值分析，给出了爆炸波在土体中的传播和桩的水平变形。Song 等对聚能装药爆炸过程进行了数值模拟，得到了土介质的动力响应、爆炸空腔的形成和发展规律以及爆炸波在土中的传播规律。

然而，感生地冲击方面的研究则十分有限，且大多是研究触地爆炸条件下的感生地冲击效应。埋置爆炸条件下土中感生地冲击的影响范围尚不明确。Alekseenko 等基于相似理论进行了相关试验研究，试验测量结果如图1 所示，得到了土中压缩波的大致分布情况以及表面区域地冲击有2 个峰值等结论。Beshara基于拟静态特性，给出了包括烈性炸药、混合气体和粉尘悬浮物在内的多种内爆气体压力的半经验关系式和预测方法，在忽略土-结构相互作用的情况下，给出了一种感生地冲击和直接地冲击的简化计算形式。Wu 等基于对地面爆炸的一系列参数化数值模拟，确定了可以应用于结构响应分析的地冲击和空气冲击波荷载。然后，他们以单层砌体填充的钢筋混凝土框架为例，计算了结构在地冲击和空气冲击波共同作用下，或单独在地冲击和空气冲击波作用下的动力响应和损伤。范俊余等结合Alekseenko 等的试验现象，对炸药地面爆炸条件下浅地表波场的分布以及作用到土中浅埋结构上的荷载进行了数值模拟研究，发现典型土中浅埋结构的顶板主要承受感生地冲击的作用，外墙主要承受直接地冲击的作用。柳锦春等基于数值模拟结果和试验数据，对根据一维平面波理论和特征线解法得到的空气冲击波为突加三角形荷载的感生地冲击的理论计算公式进行修正，提出了炸药地面接触爆炸下土中感生地冲击的实用计算方法。杨仁华等采用平面装药方法进行了核弹空爆试验模拟研究，给出了间接地冲击在黄土中的衰减规律。吴祥云等通过石灰岩中不同装药深度的爆炸试验，研究了石灰岩中装药埋深对地表空气冲击波超压的影响，给出了不同埋深爆炸地表空气冲击波超压峰值的预计方法。Krauthammer 等和Chee基于高能炸药模拟技术（high explosive simulation technique，HEST）试验，提出了一种改进的单自由度（single-degree-of-freedom，SDOF）方法，并对浅埋钢筋混凝土箱形结构在空气冲击波荷载下的受力性能进行了一系列研究。荣吉利等提出了考虑感生冲击波与直接冲击波叠加效应的核爆地冲击描述方法，并以美军核爆地冲击试验为例研究了核爆地冲击作用下土体运动特性。

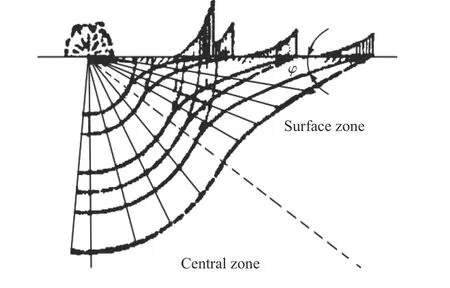
图1 波阵面的连续位置[9]Fig. 1 Successive locations of wave fronts[9]

为了研究爆炸条件下土中直接地冲击和感生地冲击的影响范围，本文中利用ANSYS/AUTODYN 软件建立二维轴对称有限元模型，开展土中爆炸地冲击效应数值模拟分析；通过黄土中爆炸试验，测得不同比例爆距上地面空气冲击波超压和土中直接地冲击竖向应力，并以此进行计算模型的验证；利用验证后的计算模型，对装药不同比例埋深和不同类型炸药的土中爆炸进行数值模拟；根据不同工况的计算结果，获得不同爆炸条件下土中感生地冲击和直接地冲击荷载的作用特征，并以此对地冲击作用区域进行划分；最后分析影响地冲击作用区的关键参数。

1 计算模型

1.1 几何模型

建立了如图2 所示的模型，该模型由炸药、空气和黄土3 部分组成，其中，对炸药和空气采用欧拉算法，对黄土采用拉格朗日算法。数值模拟中采用ANSYS/AUTODYN 软件的自动流固耦合算法。炸药装药为圆柱体，起爆点为炸药的几何中心。

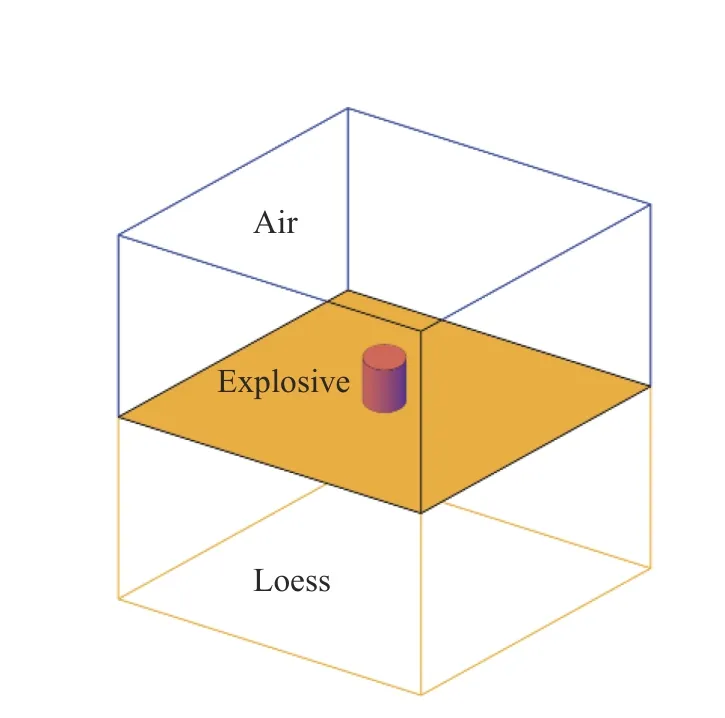
图2 爆炸模型Fig. 2 The explosion model

计算工况如表1 所示。B1～B10 为TNT 炸药不同比例埋深的工况，装药量为1 kg，比例埋深分别为-0.05、-0.025、0、0.025、0.05、0.075、0.1、0.2、0.3 和0.4 m/kg。C1～C12 为不同类型炸药的工况，不同工况以炸药的初始比内能为依据进行等效处理。炸药类型分别为ANFO、C4、EXPLOS.D、HMX、HNS 1.65、NM、PBX9407、PBX9502、PETN 1.77、SEISMOPLAS、TETRYL、TNT。

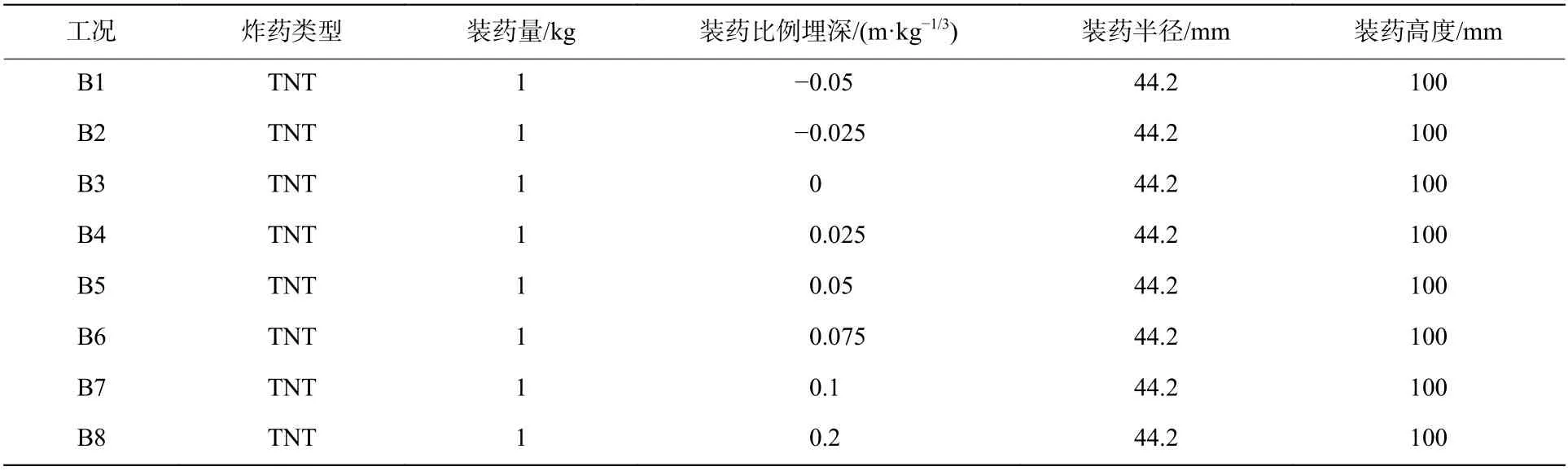
表1 计算工况Table 1 Calculation conditions

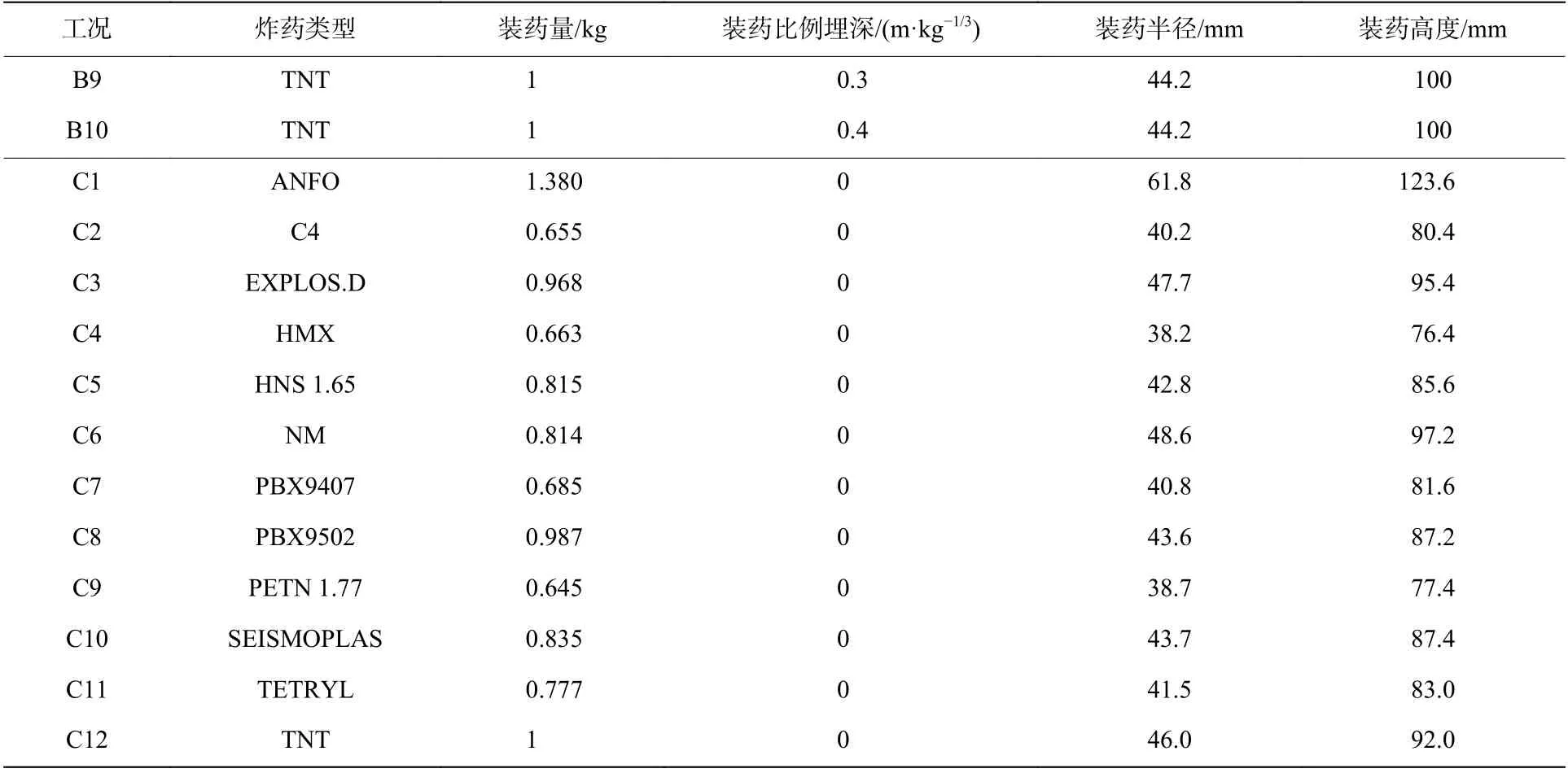
表1（续）Table 1 (Continued)

1.2 有限元模型

考虑到计算模型的对称性，建立了二维轴对称有限元模型，计算域尺寸为4 m×8 m，如图3(a)所示。其中，空气尺寸为4 m×8 m，炸药通过Fill 命令填充在空气中。如图3(b)所示，欧拉域的左边界为对称边界，其他3 条边界为流出边界。如图3(c)所示，拉格朗日域的左边界为对称边界，下边界和右边界为传输边界，其余边界为自由边界。

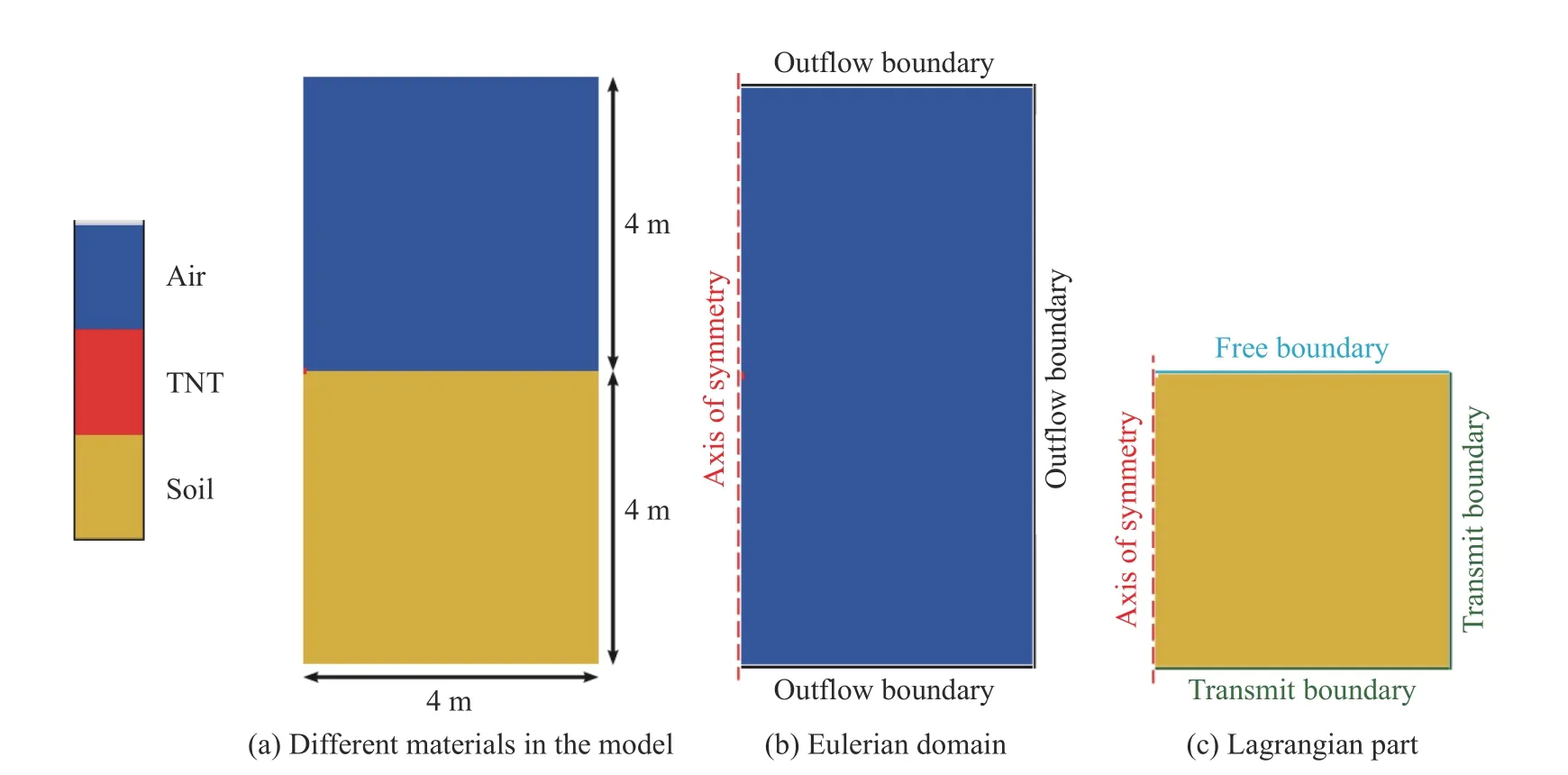
图3 有限元模型和边界条件Fig. 3 The finite element model and boundary conditions

如表1 所示，对于计算工况B1～B10，炸药尺寸为 ∅ 88.4 mm×100 mm。黄土的宽度为4 m，随装药比例埋深的增大，黄土的高度略有差别。炸药附近区域的局部放大如图4 所示，炸药放置位置以上为空气，以此模拟钻地武器的钻地效果。对于计算工况C1～C12，炸药密度和装药量的不同导致装药尺寸略有差别，黄土的宽度为4 m，高度为4 m。

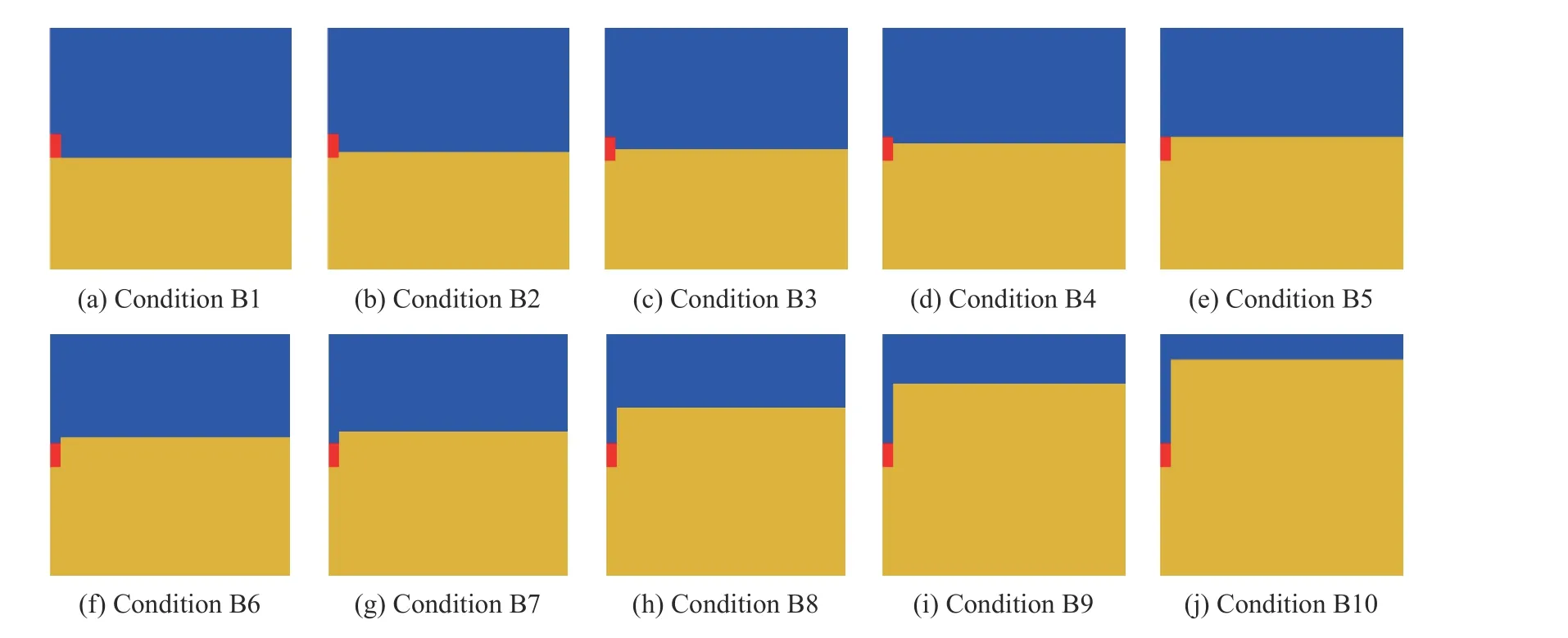
图4 工况B1～B10 下炸药附近区域的放大Fig. 4 Enlarged details near TNT under conditions B1-B10

以工况B3 为例，图5 给出了有限元模型的网格划分情况。炸药网格的径向长度为4.42 mm，高度方向长度为5 mm。对空气和黄土以炸药网格的尺寸为基础采用渐变网格，空气网格的最小尺寸为4.42 mm×5.0 mm，黄土网格的最小尺寸为8.84 mm×10.0 mm。整个有限元模型中，欧拉单元为165 000个，拉格朗日单元为36 000 个，共201 000 个单元。

图5 数值网格Fig. 5 Numerical mesh

1.3 材料模型

1.3.1 炸药

炸药采用ANSYS/AUTODYN 内置材料库中的炸药模型。Jones-Wilkins-Lee （JWL）状态方程常用来描述炸药的爆炸和膨胀，其表达式如下：

式中：γ 为理想气体等熵绝热指数，ρ 为气体密度，为初始比内能。本文中空气的初始密度为1.225 kg/m，γ=1.4，=206.8 J/g，比热容为717.6 J/(kg·K)，参考温度为288.2 K，这些参数均取自文献[25]。

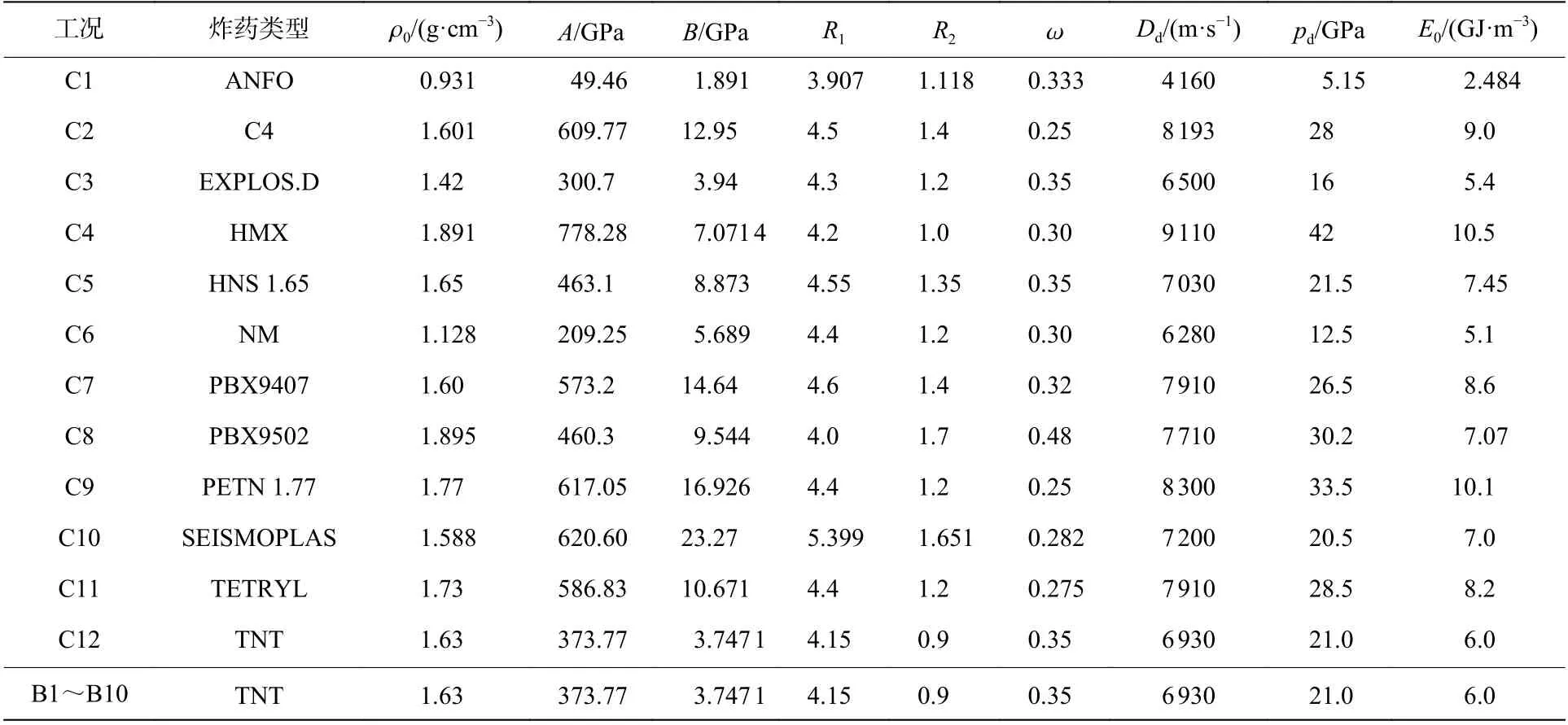
表2 炸药参数[23]Table 2 Explosive parameters[23]

1.3.3 黄土

对黄土采用ANSYS/AUTODYN 软件内置材料库中的SAND 模型。Laine 等根据砂土在动态加载条件下的响应提出了SAND 模型，并基于该模型进行了一系列数值模拟研究。SAND 模型主要包括状态方程与颗粒强度模型2 个部分。ANSYS/AUTODYN 软件中的压实态状态方程分为线性和非线性2 类，SAND 模型选用的是线性压实态状态方程。压实态状态方程还可以与多种强度模型、失效模型共同描述材料的力学行为。颗粒强度模型是Drucker-Prager 强度模型的拓展，考虑了包括粉末、黏土和砂土等颗粒介质的强度。除了压力强化效应，SAND 模型还描述了密度强化效应以及剪切模量与密度之间的函数关系。表3 为SAND 模型输入的参数值。

表3 SAND 模型参数[32-33]Table 3 Parameters of the SAND model[32-33]

试验时，土介质为洛阳地区的黄土，该黄土比重为2.54～2.84，干密度为1 200～1 790 kg/m，天然含水率为10%～15%，黏聚力为30～60 kPa，内摩擦角为15°～25°。洛阳地区黄土的压力（Pa）与体积应变 ε 的 关 系为：

因此，基于式(3) 对SAND 模型中冲击压实方程的压力与密度1 的对应关系进行修正，如表4所示。

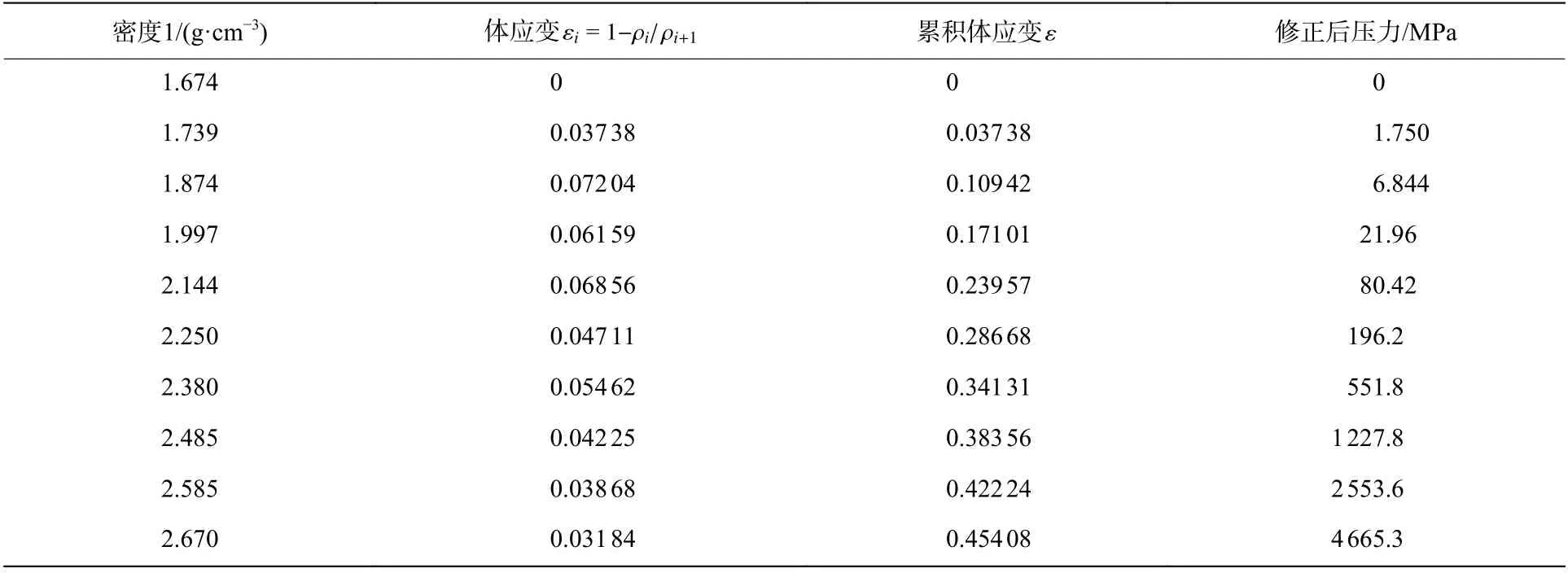
表4 线性压实状态方程中压力与密度1 的关系（基于式(3)）Table 4 Relationship between pressure and density 1 in the compaction linear equation of state(based on formula (3))

2 计算模型的试验验证

2.1 试验概况

图6 为土中接触爆炸和半埋爆炸的布置图，TNT 炸药的比例埋深分别为-0.05 和0.0 m/kg。地面布置空气冲击波超压测点A1～A4，土中爆心正下方布置直接地冲击竖向应力测点S1～S4。

图6 测试布置Fig. 6 Test arrangements

试验中采用PCB 压力传感器（见图7(a)）测试地面空气冲击波超压，采用电荷式压力传感器（见图7(b)）测试土中应力。图6 给出了8 个传感器的位置，4 个地面空气冲击波超压测点距爆心水平距离分别为0.50、0.75、1.00 和1.25 m，4 个土中直接地冲击竖向应力测点的爆心距分别为0.5、0.8、1.2 和1.7 m。回填黄土的密度控制在1 600～1 700 kg/m范围内。数据采集仪选用了东华测试公司生产的DH5960 超动态信号测试分析仪（见图7(c)），采样频率高达1 MHz。

图7 试验中的测量仪器Fig. 7 Measuring instrumentation used in test

2.2 试验方案

试验共进行2 炮次，工况见表5，试验工况E1 和E2 分别对应数值模拟中的工况B1 和B3。图8 为试验准备完成后的现场布置。炸药采用电雷管起爆，将电雷管插入炸药中间，使得起爆点接近炸药中心位置。

表5 试验工况Table 5 Test conditions

图8 试验前现场布置Fig. 8 Site layout before the test

2.3 试验结果与计算模型验证

图9 为试验后的破坏情况。将坑底回落的土进行清理后，测得试验E1 的真实爆坑直径约为69.0 cm，真实爆坑深度约为23.5 cm；试验E2 的真实爆坑直径约为87.0 cm，真实爆坑深度约为27.5 cm。根据图9 中传感器的位置判断，试验E1 的爆坑唇缘直径约为140 cm，试验E2 的爆坑唇缘直径约为160 cm。

图9 试验后破坏情况Fig. 9 Damages after the tests

采用截止频率为2 000 Hz 的低通滤波方法处理试验数据，这2 次试验中各测点的时程曲线如图10 所示，由于数据异常，部分测点未给出曲线。对比这2 次试验数据，随着装药比例埋深的增大，地面空气冲击波超压峰值减小，而土中直接地冲击应力峰值增大。图10～12 和表6 给出了试验与数值模拟结果的荷载峰值对比情况。其中，图10 测得的地下应力，在不同距离的传感器上测得波形在相同的时间均出现1 个类似的负向跳动，这是由于试验时传感器距离爆心较近，受到爆炸产生的电磁干扰。经计算，试验数据与数值模拟结果的平均偏差约为14.8%。由此表明，试验与模拟结果的一致性较好，可利用该计算模型做进一步分析研究。

表6 试验与数值模拟荷载峰值Table 6 Peak loads obtained by tests and simulations

表6（续）Table 6 (Continued)

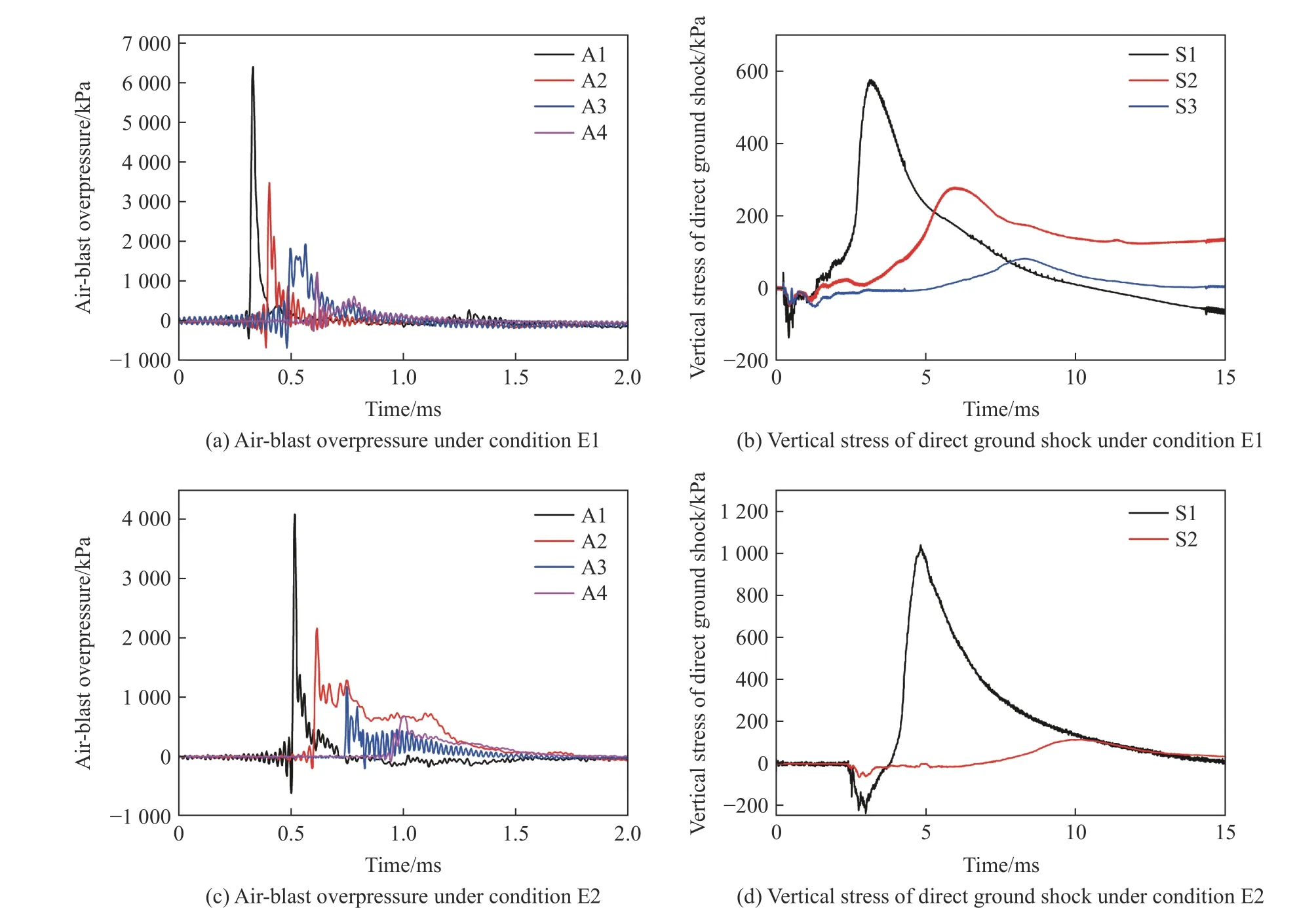
图10 地面空气冲击波超压和土中直接地冲击竖向应力时程曲线试验结果Fig. 10 Tested time history curves of air-blast overpressure and vertical stress of direct ground shock

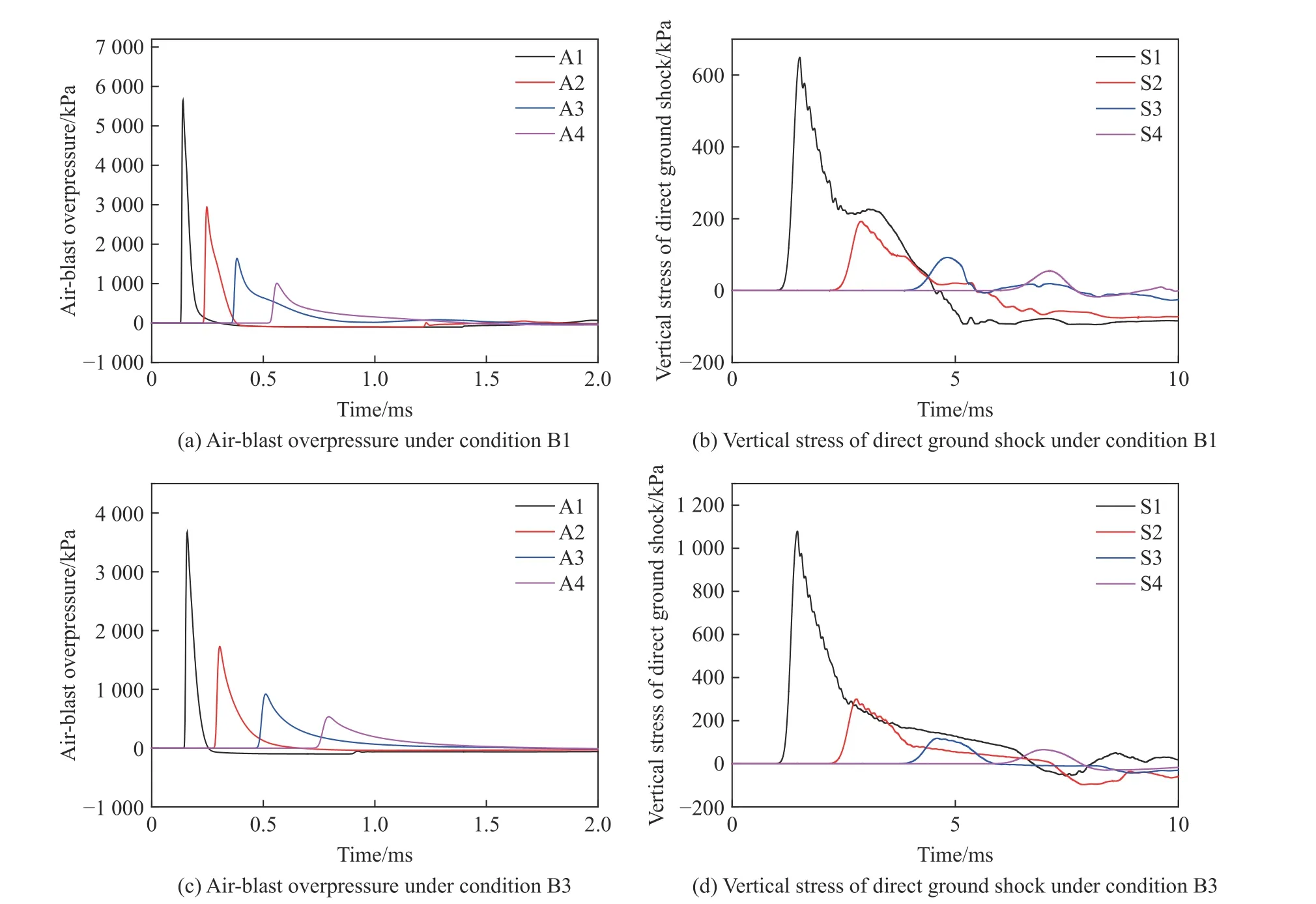
图11 地面空气冲击波超压和土中直接地冲击竖向应力时程曲线数值模拟结果Fig. 11 Numerically-simulated time history curves of air-blast overpressure and vertical stress of direct ground shock

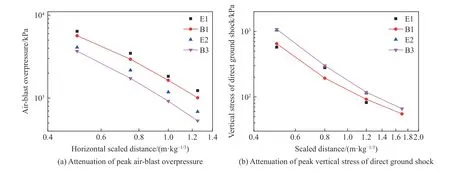
图12 试验与数值模拟数据对比Fig. 12 Comparison of tests and simulations

3 地冲击作用分区

3.1 感生地冲击影响范围

基于已验证的计算模型，对土中爆炸地冲击效应作进一步数值模拟研究。以工况B3 为例，其压力云图如图13 所示，从图中发现土中应力波的时空分布与图1相符，可将地冲击作用区域划分为表面区（即区域A 和B）和中心区（区域C）。

图13 工况B3 下的压力云图Fig. 13 Pressure contours under condition B3

图14(a)为表面区中地下5 cm 处压力时程曲线，该时程曲线存在2 个明显的峰值（即感生地冲击峰值和直接地冲击峰值）。图14(b)为中心区中地下40 cm 处压力时程曲线，该时程曲线只存在1 个峰值（即直接地冲击峰值）。由地下5 cm 至地下40 cm 处的压力时程曲线从2 个峰值减少为1 个峰值，表明随着深度的增加，地冲击作用区域的受力特征从感生地冲击与直接地冲击共同作用演变为主要受直接地冲击作用。进一步分析表面区的受力特征，如图15(a)所示，在区域A 中地下20 cm 处的竖向应力时程曲线存在2 个峰值，且感生地冲击应力峰值明显大于直接地冲击应力峰值，此时感生地冲击起主导作用。随着深度增加，在区域B 中地下35 cm 处的竖向应力时程曲线如图15(b)所示，此时同样存在2 个峰值，但感生地冲击应力峰值与直接地冲击应力峰值相当，说明该区域受感生地冲击和直接地冲击联合作用。根据表面区中不同深度竖向应力的特征，将表面区划分为地表区（区域A）和近地表区（区域B）。图14 和图15 中地下测点具体位置在图13 中用红色点进行标注。

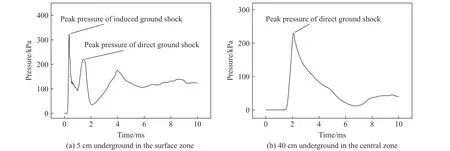
图14 工况B3 下爆心水平距离0.5 m 处的压力时程曲线Fig. 14 Pressure-time curves at the horizontal distance of 0.5 m from the detonation point under condition B3

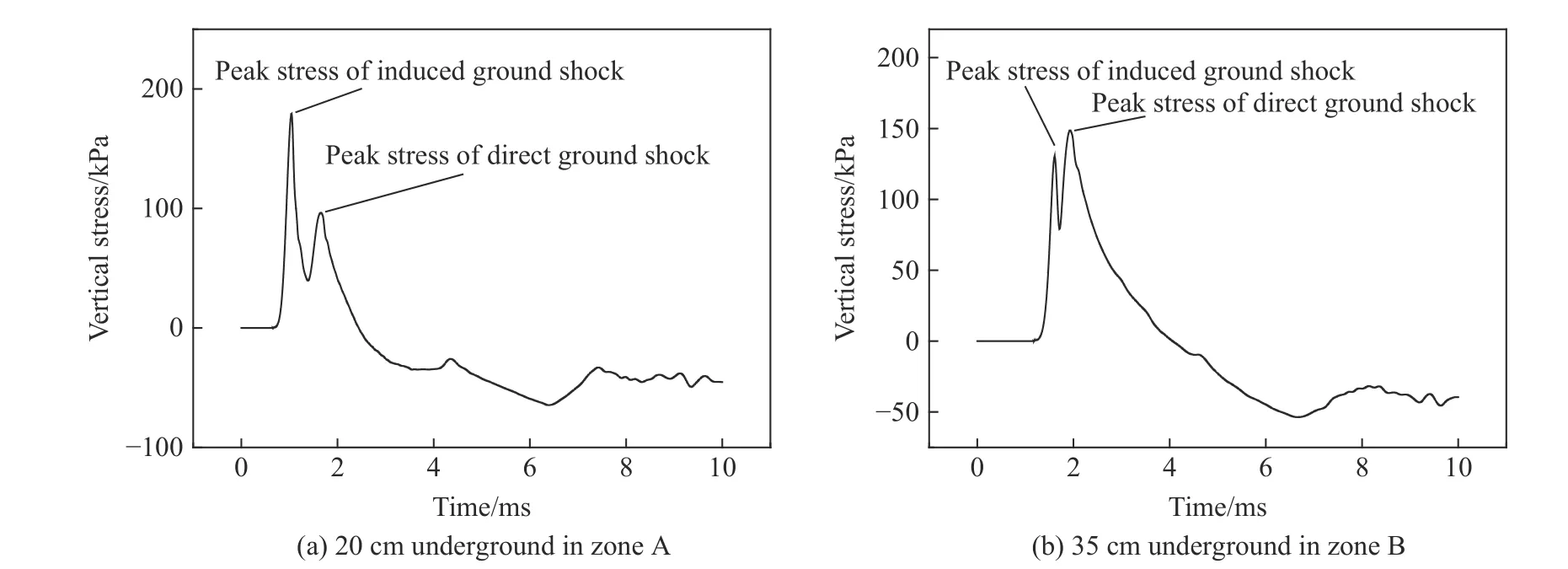
图15 工况B3 下爆心水平距离0.5 m 处竖向应力时程曲线Fig. 15 Vertical stress time curves at the horizontal distance of 0.5 m from the detonation point under condition B3

3.2 装药比例埋深的影响

图16 是工况B1～B10 下1.0 ms 时的压力云图，为了方便对比，压力云图截取了炸药周围2.5 m×3.5 m 的区域。图16 的压力云图采用了相同的标尺，可以发现相同时刻下，随着装药比例埋深的增加，黄土中直接地冲击的作用范围和压力值逐渐增大，而接近地面处空气冲击波的作用范围和压力值逐渐减小。

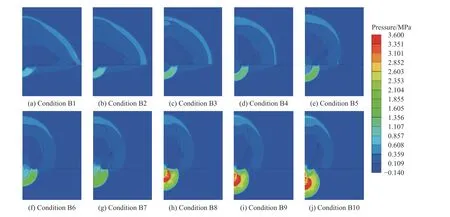
图16 工况B1～B10 下1.0 ms 时的压力云图Fig. 16 Pressure contours at 1.0 ms under conditions B1-B10

图17 以工况B3 为例，给出了数值模拟的总能量时程曲线和计算模型中空气、黄土和TNT 的动能时程曲线。由图17(a)可知，在6.4 ms 左右，空气冲击波到达流出边界，随后空气冲击波溢出流出边界，导致计算模型的能量逐渐降低。在6.4 ms 时，能量守恒误差为2.479×10J，计算模型能量为5.377×10J，能量守恒误差约为计算模型能量的0.46%；在计算终止时刻10 ms 时，能量守恒误差为2.532×10J，计算模型能量为4.898×10J，能量守恒误差约为计算模型能量的0.52%。由图17(b)可知，计算模型中空气、黄土和TNT 炸药的动能达到峰值的时间均在1 ms 以内，此时空气冲击波尚未溢出流出边界。

图17 工况B3 下的能量时程曲线Fig. 17 Energy time history curves under condition B3

图18 给出了空气和黄土的动能峰值随装药比例埋深的变化情况。随装药比例埋深的增加，空气的动能峰值迅速减小，在装药比例埋深达到0.1 m/kg后趋于稳定；黄土的动能峰值迅速增大，在装药比例埋深达到0.05 m/kg后趋于稳定。这说明随着装药比例埋深的增加，空气冲击波获得的能量越来越少，更多的能量耦合进入黄土介质，这将导致感生地冲击影响范围减小。

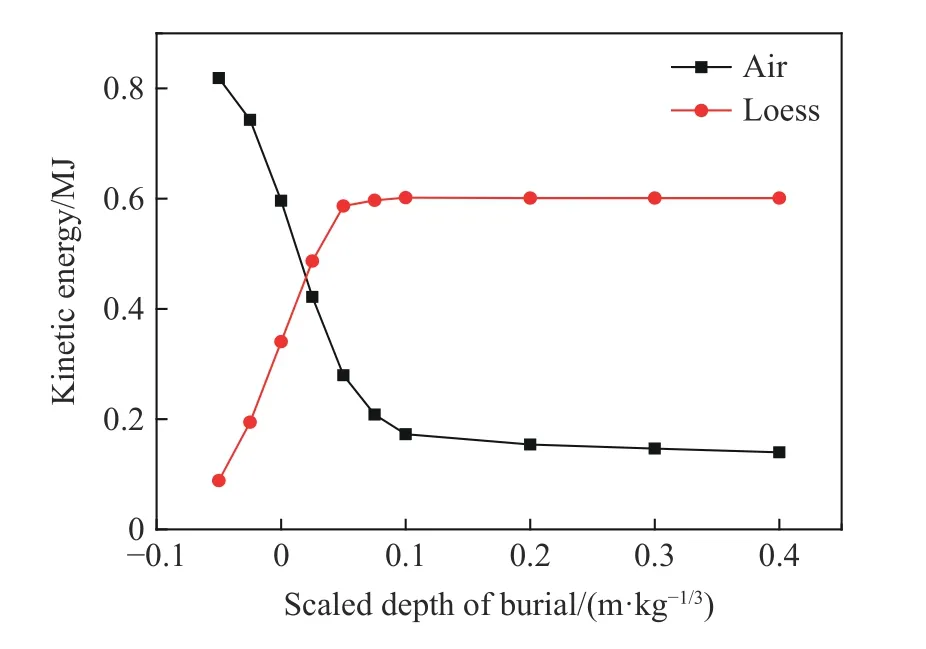
图18 工况B1～B10 下空气和黄土的动能峰值随装药比例埋深的变化Fig. 18 Peak kinetic energy of air and loess varying with charge scaled depth of burial under conditions B1-B10

如图19(a) 所示，以地平线为角的一条边，以对称轴和地平线的交点为顶点；从距离点水平距离500 mm 处的点向下选取数据测点。通过对比分析点正下方不同深度处数据测点的压力时程曲线，同时根据压力云图中波阵面经过数据测点的大致时间，可以发现，随着深度的加深，感生地冲击压力峰值迅速减小。在一定深度后，从压力时程曲线上只能观察到直接地冲击峰值，观察不到感生地冲击峰值。图19(b)仅展示部分数据测点，实际为了判断准确，所取数据测点间隔更小。存在某一深度处测点的压力时程曲线从2 个明显的峰值转变为1 个明显的峰值，取这一点为点，用90°减去∠即为γ 的大小。然后，对比点和点之间的数据测点的竖向应力时程曲线（见图19(c)），可以发现，随着深度的增加，感生地冲击竖向应力峰值减小，直接地冲击竖向应力峰值增大。存在某一深度处测点的竖向应力时程曲线中，感生地冲击和直接地冲击的竖向应力峰值相等，取这一点为点，则∠=α，∠-∠=β。

图19 α、β 和γ 的取值方法Fig. 19 Determination methods of α, β and γ

图20 给出了工况B1～B10 下的数值模拟结果。其中，α、β 和γ 分别表示图13 中地表区、近地表区和中心区的角度，且α、β 和γ 三者之和为90°。随装药比例埋深的增大，α、β 和γ 的变化呈较强的规律性。

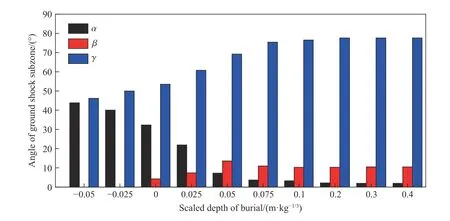
图20 工况B1～B10 下地冲击作用区的角度随装药比例埋深的变化Fig. 20 Angles of ground shock subzones varying with charge scaled depth of burial under conditions B1-B10

(1)当装药比例埋深为-0.05～0.075 m/kg时，地冲击作用区角度的变化较剧烈。随着装药比例埋深的增加，中心区的角度γ 迅速增大，地表区的角度α 迅速减小，近地表区的角度β 逐渐增大。

(2)当装药比例埋深为0.1～0.4 m/kg时，地冲击作用区的角度趋于稳定。

3.3 炸药类型的影响

图21 为工况C1～C12 下1.0 ms 时的压力云图，同样截取了炸药周围2.5 m×3.5 m 的区域。图22 给出了不同工况下空气和黄土的动能峰值的变化情况。不同工况下，直接地冲击和感生地冲击压力值不同，爆炸耦合进入空气和黄土介质动能存在差异，这将引起不同工况地冲击作用区角度的变化。

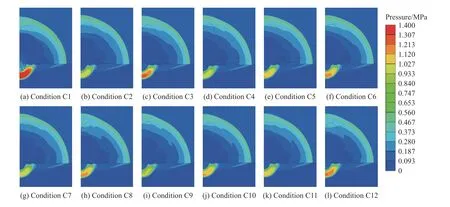
图21 工况C1～C12 下1.0 ms 时的压力云图Fig. 21 Pressure contours at 1.0 ms under conditions C1-C12

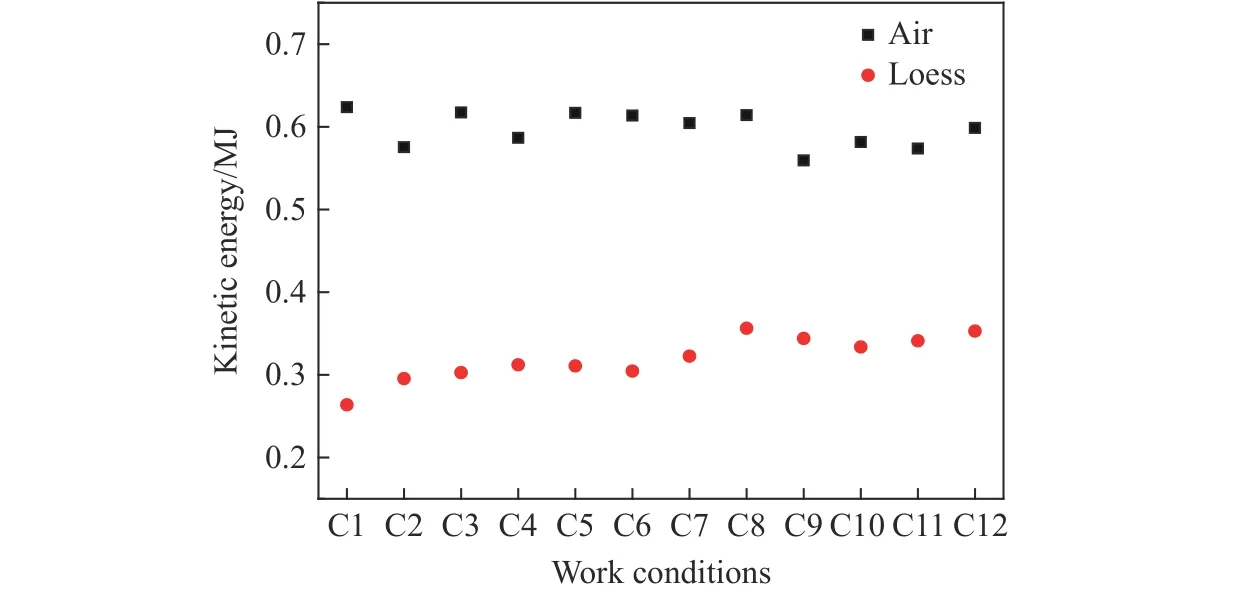
图22 工况C1～C12 下空气和黄土的动能峰值Fig. 22 Peak kinetic energy of air and loess under conditions C1-C12

表7 给出了工况C1～C12 下的数值模拟结果。表7 中：为水平爆心距0.5 m 处地面空气冲击波超压峰值，σ为爆心正下方0.5 m 处直接地冲击应力峰值，其位置可参见图6(b)）中A1 和S1 测点；为水平爆心距0.5 m 处地面空气冲击波超压的冲量，为爆心正下方0.5 m 处直接地冲击应力的冲量。由图23可知，/随炸药爆速和爆压的升高呈增大的趋势，即随着炸药爆速和爆压的升高，地面空气冲击波超压的冲量增大，而直接地冲击应力的冲量减小。

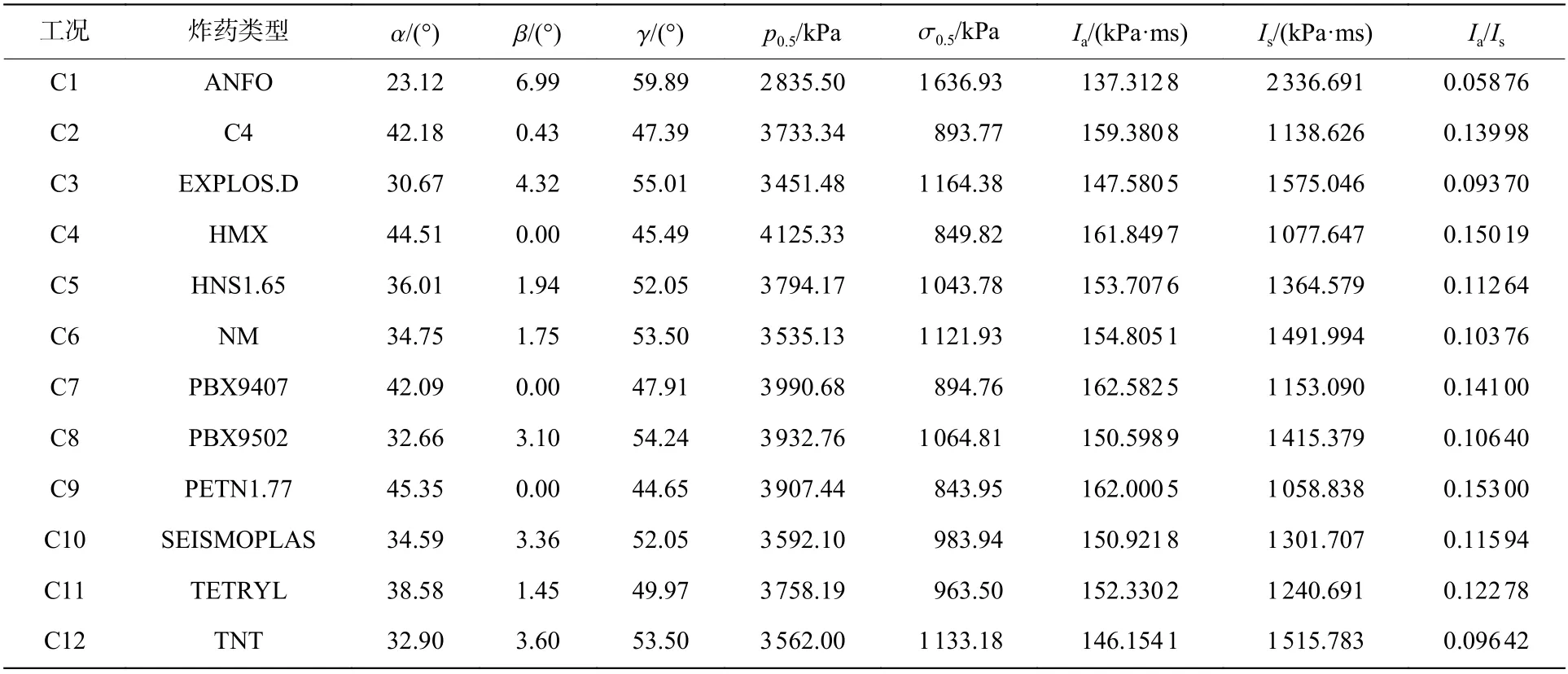
表7 工况C1～C12 下的数值模拟结果Table 7 Numerically simulated results under conditions C1-C12

图23 Ia/Is 随炸药爆速和爆压的变化Fig. 23 Variation of Ia/Is with detonation velocity and detonation pressure of explosive

经分析，发现当/的取值范围为0.058 76～0.153 00 时，地冲击作用区角度与地面空气冲击波超压冲量和直接地冲击应力冲量之比呈线性相关关系（见图24），拟合后可得到：

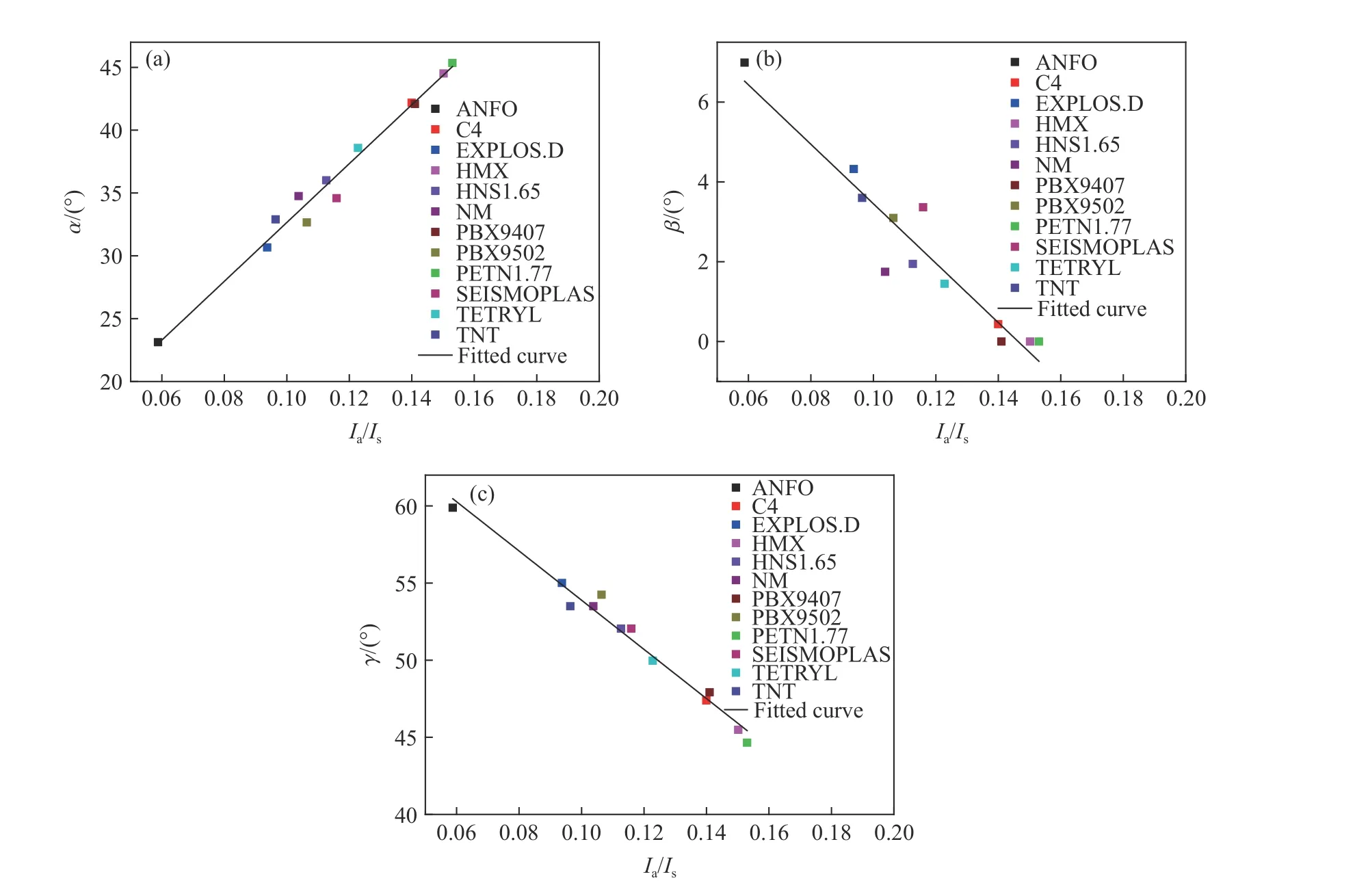
图24 α、β 和γ 随Ia/Is 的变化Fig. 24 Variation of α, β and γ with Ia/Is

式中：α、β 和γ 的单位均为(°)。

4 结 论

针对土中爆炸应力波的时空分布问题，以数值模拟分析为主要手段，并辅以土中爆炸试验，得到以下主要结论。

(1)通过黄土中接触爆炸和半埋爆炸试验，得到了不同比例爆距上地面空气冲击波超压和土中直接地冲击竖向应力，并以此验证了所建立计算模型的有效性。

(2)根据土中不同深度压力和竖向应力的特征，将土中应力波场划分为地表区、近地表区和中心区。地表区的时程曲线出现2 个峰值，且感生地冲击起主导作用；近地表区的时程曲线同样出现2 个峰值，且受感生地冲击和直接地冲击的联合作用；中心区的时程曲线仅出现1 个峰值，主要受直接地冲击的作用。

(3)通过研究不同装药比例埋深爆炸工况，发现当装药比例埋深为-0.05～0.075 m/kg时，随着装药比例埋深的增加，土中应力波场的中心区迅速增大，地表区迅速减小，近地表区逐渐增大；当装药比例埋深为0.1～0.4 m/kg时，地冲击作用区的分布趋于稳定。

(4)通过研究装药比例埋深为0.0 m/kg时，不同类型炸药爆炸工况，发现随着炸药爆速和爆压的增加，地面空气冲击波超压的冲量增大，而直接地冲击应力的冲量减小，在一定范围内，地冲击作用区角度与地面空气冲击波超压冲量和直接地冲击应力冲量之比呈线性相关关系。