锥形长药柱水下爆炸冲击波参数计算方法*

徐维铮，黄 超，张 磐，黄 宇，曾 繁，王 星，郑贤旭

（1. 中国工程物理研究院流体物理研究所，四川 绵阳 621999；2. 中国工程物理研究院高性能数值模拟软件中心，北京 100088；3. 北京应用物理与计算数学研究所，北京 100088）

水下爆炸与空中爆炸相比，由于水介质的密度和可压缩性远不同于空气，形成的冲击波具有压力衰减慢、脉宽短的特点。而在水下强爆炸实验中，有些情况下需要用到具有长脉宽特性的冲击波，如利用小当量装药来模拟大当量装药（如吨级以上）的水下爆炸问题，可以在一定程度上实现冲击波能的等效，这样的需求可以采用锥形长药柱技术来满足。通过调整锥形长药柱的形状和参数，能够对冲击波压力-时间曲线的波形进行控制，进而设计出满足实验需求的装药。锥形长药柱是由多个圆台形状的炸药首尾相连组成的细长装药，图1 所示为典型的双锥形长药柱结构。所谓“双锥”是指装药圆锥的母线与轴线之间的夹角有2 个值，如果只有1 个值则称为“单锥”。锥形长药柱从直径小的一端起爆，完成爆轰的时间由装药的总长度控制，水下爆炸时能够在起爆端一侧形成具有长脉宽特征的冲击波，而在其他方位形成的冲击波则各异，即冲击波压力具有各向异性。

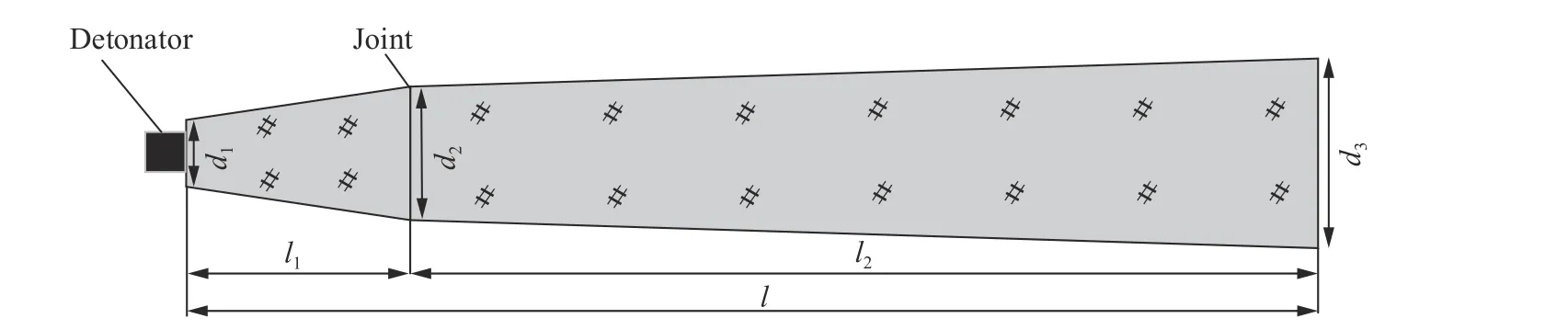
图1 锥形长药柱结构示意图Fig. 1 Construction of a cone-shaped charge

对于具有细长结构特征装药的水下爆炸研究，已有的工作大多是基于圆柱形装药。如根据Cole对圆柱装药实验结果的描述：对于长径比约15 的圆柱形药包，在距离6.10 m 处观测到药包周围压力-时间曲线的差异，这种差异在30.50～150.00 m 处仍然能够发现；在距长径比为1.4、质量为0.25 kg 的粉状特屈儿药包1.07 m 处，雷管一侧的压力比另一端的压力高。Sternberg采用Lagrangian 程序计算了长径比为1～7 的圆柱形装药的水下爆炸冲击波，发现在起爆端一侧的冲击波压力幅值较低，但持续时间更长，对应做功的有效能量更多。Hammond通过水下爆炸实验测试了 ∅ 0.222 m×1.333 m（长径比为6）的圆柱形装药，发现在比例距离/＜3.5 m/kg（为爆距，为装药TNT 当量）范围内冲击波的压力幅值和持续时间与装药形状和朝向密切相关。刘磊等采用AUTODYN 数值模拟软件研究了长径比为0.33～3.00 的圆柱形装药水下爆炸冲击波，发现柱形装药冲击波压力峰值分布与等量球形装药之间存在映射关系，但仅研究了压力峰值的规律，且缺少实验数据的验证。张弛宇等采用映射方法推导了圆柱形装药不同方位冲击波压力的经验公式，但只能计算冲击波的峰值压力，无法获得压力波形。Huang 等研究了长径比为2.0～9.2 的圆柱形装药的冲击波效应场和气泡运动，确认了装药附近不同方位的冲击波压力特征的差异，这种差异对气泡坍塌和射流行为也有影响。Zhang 等对成形装药水下爆炸冲击波的数值模拟研究也发现装药轴向与径向冲击波的峰值压力存在差异。

上述工作主要研究了圆柱形装药水下爆炸冲击波压力场的各向异性规律。现有的经验公式只能计算圆柱装药周围的冲击波峰值压力，而无法计算冲击波的压力-时间曲线。对于具有锥形结构或有形状变化的长药柱，目前还没有用于直接计算水下爆炸冲击波压力-时间曲线的经验公式。本文中，以锥形长药柱为对象，建立其水下爆炸冲击波压力-时间曲线的计算方法，并通过实验验证其有效性，在此基础上研究冲击波的压力剖面特征和峰值压力分布规律。

1 计算方法

由于基于球形装药的冲击波经验公式没有考虑爆源的形状因素，对于长药柱显然是不适用的。为了解决这一问题，就需要对锥形长药柱的水下爆炸冲击波进行建模。首先，锥形装药通常用于模拟大当量装药的远场冲击波，强度一般在兆帕量级，可看成弱冲击波，这样就可以基于声学近似假设对问题进行简化。其次，在声学理论中波动方程是线性的，那么流场中的压力扰动可以通过叠加得到。基于以上分析，可以对锥形长药柱水下爆炸冲击波进行预测估算，将细长的锥形长药柱划分为若干个小药包，然后按照爆轰波的传播顺序，将各个小药包在水中产生的冲击波压力进行叠加，从而得到整个锥形长药柱的冲击波压力曲线。

为了计算整个锥形长药柱的冲击波压力，首先要精确获得每个小药包产生的冲击波压力。水下爆炸冲击波压力曲线常采用指数衰减模型描述：

图2 冲击波压力的指数衰减模型Fig. 2 Fit of the shock-wave pressure profile by exponential models

下面针对锥形长药柱结构进行分析。图3 给出了双锥长药柱的分段示意图，起爆端位于180°方位，以装药中心为原点，把装药沿着方向划分为段，将每段炸药视为单独的装药，各分段的装药量相差也不大，这样就可以利用声学近似理论将不同分段的冲击波压力进行叠加，从而得到指定测点（,）处的爆炸冲击波压力。根据Sternberg的结论，长径比为1 的装药各个方位测得的冲击波压力与同等质量球形装药的一样。由于锥形长药柱的直径是不断变化的，在装药划分时可将每个小药包的长径比取为1 左右，这样就可以用前述公式来计算每个小药包产生的冲击波压力。基于类似Wilkins 提出的燃烧分数模型，对锥形长药柱采用时序爆轰模型进行控制，每个小药包的起爆时间由其几何中心的位置和炸药的爆速决定。

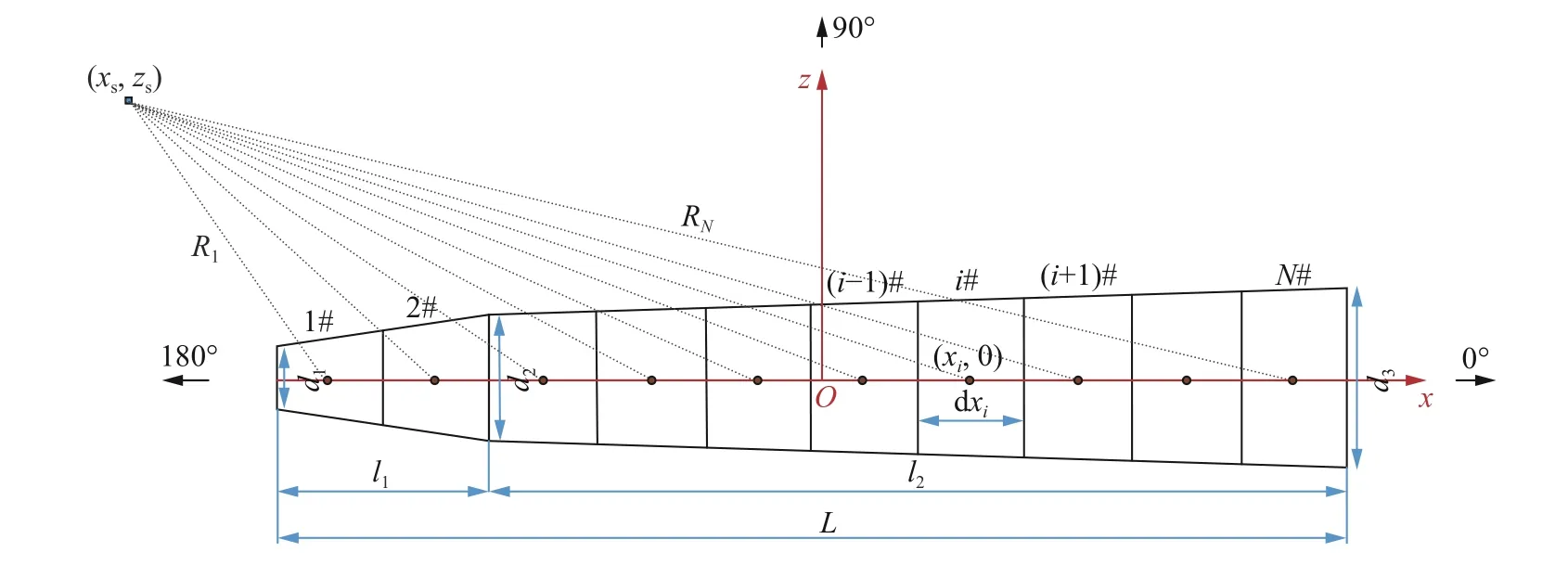
图3 锥形长药柱分段示意图Fig. 3 Discretization of the cone-shaped charge into subsegments

各分段装药从左向右依次起爆，这样多个分段装药的冲击波形成叠加，就可以计算得到水中指定测点（,）处的冲击波压力：

冲击波的相互作用非常复杂，边角处相邻冲击波碰撞后会形成反射冲击波和马赫杆。此外，后段装药形成的冲击波不仅在已经被冲击压缩的水介质中传播，同时也会在已反应炸药中传播，并从爆轰产物-水界面传播到水中，导致最终到达测点的冲击波压力降低。因此，必须考虑冲击波相互作用的非线性效应，采用下式对冲击波压力进行修正：

式中：A为峰值压力的修正因数，取A= 0.5/t，t为第段装药的冲击波到达测点经历的时间。这样每个修正因数是不同的，主要考虑了测点相对位置的影响，即不同分段装药的冲击波到达叠加点的过程存在差异，第段装药到达测点的冲击波会受到第1 段～第（-1）段装药到达测点的冲击波的影响。为时间常数θ的修正因数，在（0,1）范围内取值，可先取为1，对于本文中的装药结构，在获得一定量的实验数据后进一步修正为0.5。

由于装药形状和起爆方式对水下爆炸压力分布的影响主要在近场，中远场基本已经匀化，差异不会很大，这里有必要对上述计算模型的适用范围进行限定。Bjarnholt根据大量应用经验和分析指出，装药的形状、起爆方式等会对水下爆炸冲击波的压力测量产生影响，并且给出了避免这些影响的比例距离范围为/＜3.5 m/kg。比例距离的下限则应限定在气泡的最大半径之外，与装药类型和水深有关，可按经验公式进行估算。因此，对于TNT 装药，计算模型的适用范围可取为：

式中：为装药质量，kg；为水深，m。

2 实验验证

2.1 实验样品

为了对上述计算模型进行测试，设计了2 种锥形长药柱结构，如图4 所示，其几何参数和材料参数如表1～2 所示，ρ 为密度，为爆轰速度，为声速。计算用到的炸药常数按照装药类型和密度取自文献[11]。

表1 锥形长药柱几何参数Table 1 Geometric parameters for the slender cone-shaped charges

图4 锥形长药柱几何结构示意图Fig. 4 Structures of slender cone-shaped charges

表2 锥形长药柱材料参数Table 2 Material parameters for the slender cone-shaped charges

2.2 实验布局

将锥形长药柱水平吊放在爆炸水池中央，其几何中心轴距水面10 m。在装药几何中心轴所在的深度平面上，与锥形长药柱轴线夹角180、120、105、90、0方向，距离装药中心3、4、6、8 m 处布置PCB138A 型水中压力传感器（共12 个），见图5，记录不同角度方向上、不同距离处的冲击波压力时间历程。

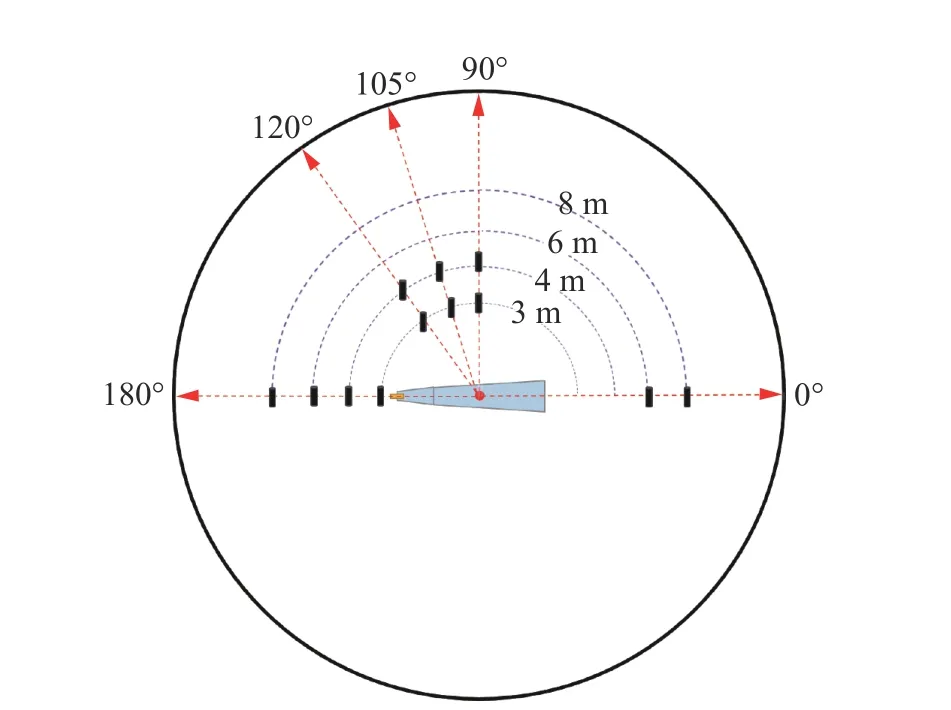
图5 锥形长药柱水中冲击波测试示意图Fig. 5 Measurement of underwater shock waves induced by a cone-shaped charge

实验测试系统由同步机、起爆台、示波器，适调仪、PCB 水中压力传感器等组成，系统的框图如图6 所示。测试系统由同步机主控，其输出的同步信号同时触发起爆台、记录压力信号的示波器；起爆台起爆炸药装置中的雷管并引爆炸药，锥形长药柱水中爆炸冲击波作用于PCB138水中压力传感器产生电压信号，经信号适调仪传输至示波器记录。实验前采用8 kg 标准TNT 药球对测试系统中压力传感器的灵敏度进行动态标定，测试系统的测试精度控制在5%以内。

图6 测试系统示意图Fig. 6 Construction of the measurement system

2.3 实验结果

实验结果和计算结果均在图7 中给出，比较了距离2 种锥形长药柱中心4 m 和6 m 处起爆端（180°）、侧面（90°）和远离起爆端（0°）3 个方位的冲击波压力-时间曲线。

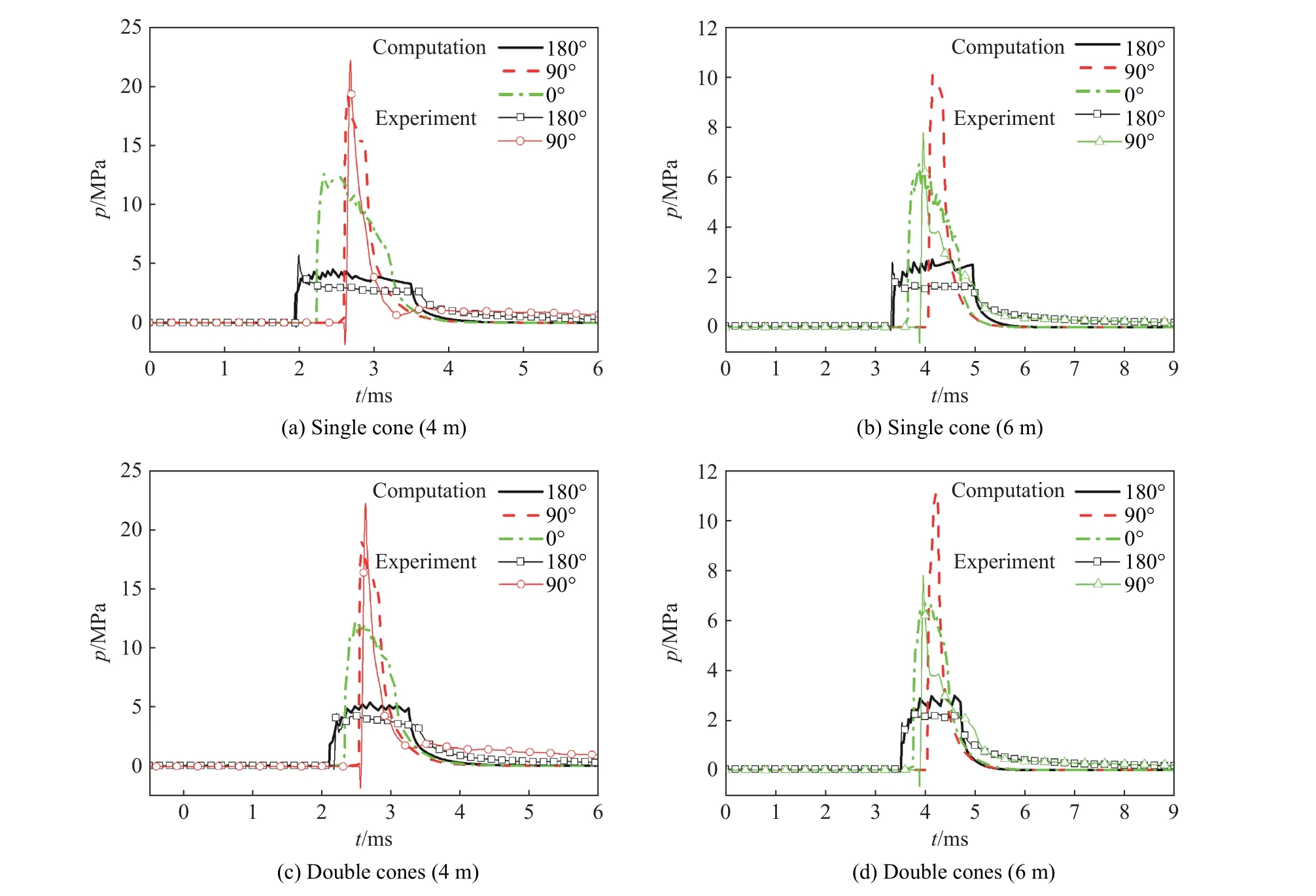
图7 锥形长药柱0°、90°、180°方位的冲击波压力曲线对比Fig. 7 Comparison of the pressure curves in the directions of 0°, 90° and 180° at different distances from the centers of the slender cone-shaped charges

总体上看，计算结果较好地捕捉到了不同方位冲击波压力曲线的主要特征，包括冲击波的到达时间、压力幅值和持续时间。对于冲击波的到达时间，起爆端一侧的冲击波最先达到，其次是远离起爆端一侧的冲击波，装药侧面的冲击波最晚达到。由于计算模型中采用的是平均冲击波速度，实验测到的冲击波到达时间与数值模拟结果存在微小差异，但不同方位冲击波的到达时间顺序是一致的，误差约为5%。对于冲击波的压力幅值，计算结果与实验结果基本在同一水平，起爆端一侧的冲击波压力最低，装药侧面的冲击波压力最高，远离起爆端一侧的冲击波压力介于前两者之间。对于冲击波的持续时间，在起爆端一侧叠加形成的冲击波的平台特征非常明显，说明形成的冲击波具有长脉宽特征。这是由于冲击波叠加的持续时间是从起爆端的冲击波达到测点的时刻开始，一直持续到远离起爆端一侧的冲击波到达测点的时刻为止。单锥装药压力平台持续时间的计算值约为1.53 ms，双锥装药压力平台持续时间的计算值约为1.14 ms，与实验测得的1.64 ms 和1.22 ms 基本接近，误差均在10%以内。因此，可以认为对于锥形长药柱水下爆炸冲击波压力的预估，本文中提出的计算模型可以满足工程应用需求。

3 冲击波压力和脉宽分布规律

计算和实验结果表明，锥形长药柱周围流场中的冲击波存在各向异性特征，即在不同的方位角方向，冲击波的压力幅值和脉宽（持续时间）均存在比较明显的差异。为了获得装药周围流场中冲击波压力和脉宽的分布规律，需要对装药不同方位的冲击波数据进行分析。由于实验数据有限，除模型计算外，还采用LS-DYNA 数值计算了装药周围流场中的冲击波压力。数值模型按照实验算例的布置建模，采用二维轴对称模型，计算域为 ∅ 8 m×16 m，装药置于模型的中心，网格总数为128 万。

图8 给出了距离锥形装药中心3 m 处，冲击波峰值压力的计算和数值模拟结果在三维幅值空间中的对比。从图8 可以看到，计算得到的冲击波峰值压力幅值图的形状相似，均呈扁平状，峰值压力的幅值在装药的轴向两端（起爆端和与其相对的一端）较低，而在侧面的幅值则较高。

图8 距离锥形装药中心3 m 处不同方位的冲击波峰值压力对比（三维幅值图）Fig. 8 Comparison of the peak pressures at 3 m from the centers of the cone-shaped charges (three-dimensional amplitude plots)

为了进一步与实验结果进行对比分析，将图8 的数据转换到极坐标系下，如图9 所示，给出了距离装药中心3 m 处，沿着圆锥母线不同方位冲击波峰值压力的对比。可以看到，锥形长药柱冲击波的峰值压力呈明显的非球对称分布，从起爆端到远离起爆端的变化，呈先升高再降低的趋势，在装药侧面（约75°）最大。在装药侧面（60°～90°和270°～300°）冲击波的峰值压力显著高于其他区域，这是冲击波在装药侧面叠加的效果；在起爆端一侧，180°方位冲击波的峰值压力最低；在远离起爆端一侧，0°方位冲击波的峰值压力也相对较低，但高于180°方位的冲击波峰值压力。这些规律与圆柱形装药的研究结果相似，但由于装药长径比很大，冲击波峰值压力的各向异性更显著。另外，锥形长药柱冲击波峰值压力的模型计算结果与数值模拟结果在大部分区域吻合较好。在装药侧面的预测结果较高，这是由于在装药侧面冲击波的脉宽较短，各分段装药的冲击波在相对短的时间内叠加，导致计算出的压力偏高。

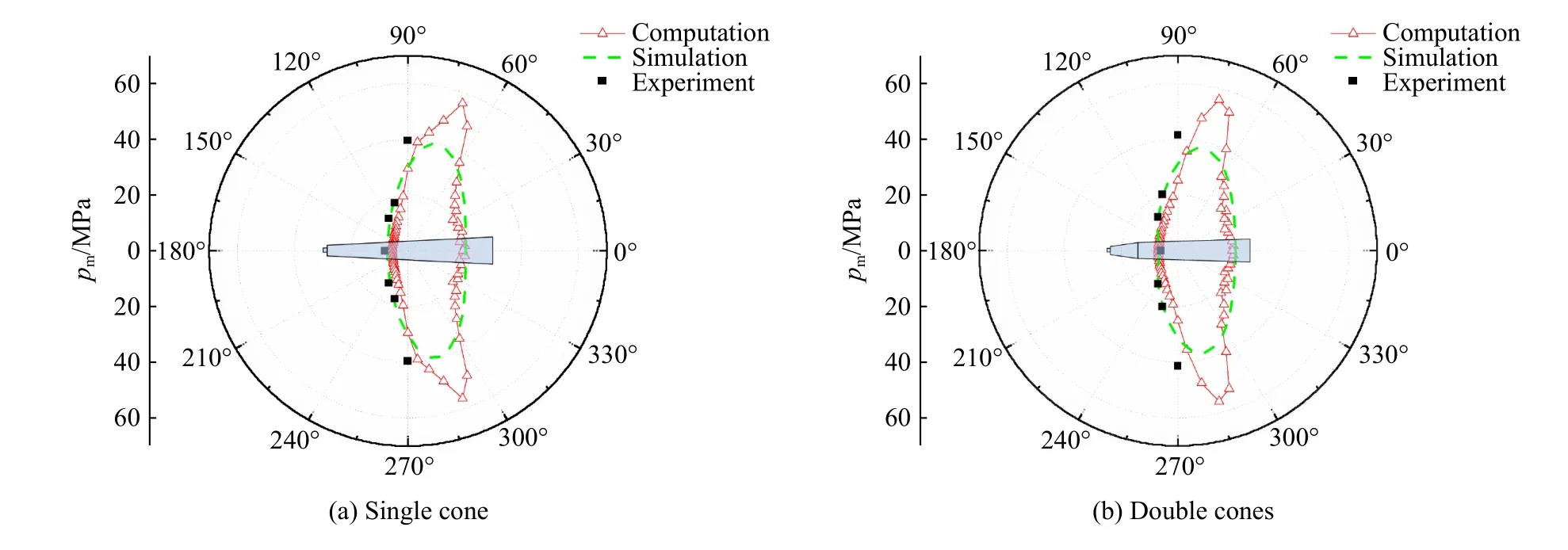
图9 距离锥形装药中心3 m 处不同方位的冲击波峰值压力（极坐标图）Fig. 9 Distributions of the peak pressures at 3 m from the centers of the cone-shaped charges (polar coordinate plots)

图10 为极坐标系下，距离锥形装药中心3 m 处，沿着圆锥母线不同方位冲击波脉宽的对比。可以看到，模型计算结果与数值模拟、实验的结果吻合很好。对于流场中的任一测点，冲击波的持续时间近似等于最后到达的冲击波与最先到达的冲击波的时间差，即冲击波的脉宽主要与炸药的爆速和冲击波在水中的传播速度有关。冲击波的持续时间从起爆端到远离起爆端的变化呈先缩短再延长的趋势，在装药侧面（约75°）冲击波的持续时间最短，与冲击波峰值压力的分布规律正好相反。

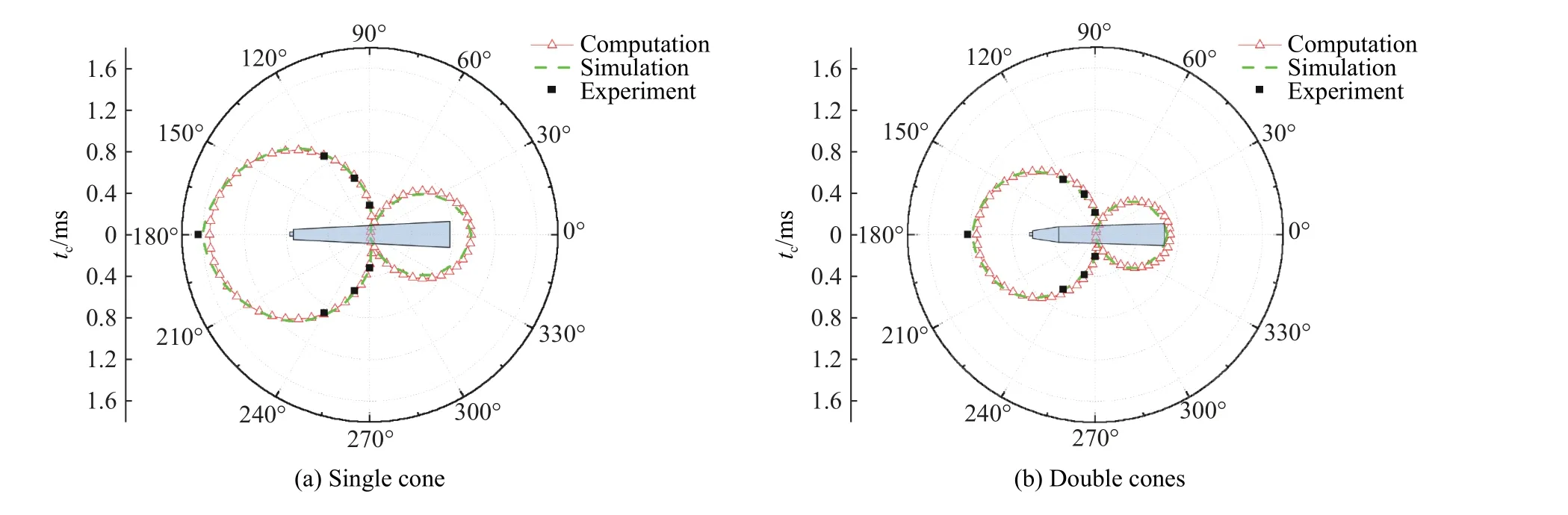
图10 距离锥形装药中心3 m 处不同方位的冲击波脉宽（极坐标图）Fig. 10 Distributions of the pressure duration at 3 m from the centers of the cone-shaped charges (polar coordinate plots)

总体上看，锥形长药柱与球形装药冲击波分布存在着明显的差异，这主要是由于装药形状和起爆方式的改变所导致的。在锥形长药柱周围流场中形成的冲击波压力分布具有方向性，在起爆端一侧的冲击波压力较低但脉宽较长，在装药侧面的冲击波压力较高但脉宽较短，而在远离起爆端一侧冲击波的压力和脉宽介于前两者之间。

4 结 论

针对锥形长药柱水下爆炸冲击波压力经验公式和工程算法的需求，基于分段叠加方法建立了能够估算冲击波压力分布和波形曲线的计算模型，并通过实验进行了验证，在此基础上研究了不同形状锥形长药柱水下爆炸冲击波的压力和脉宽分布规律，得到以下结论。

（1）基于叠加原理对水下爆炸冲击波压力进行参数化建模是可行的，在限定的距离范围内，模型计算结果与实验、数值模拟得到的规律基本一致，为工程应用提供了一种可用的快速计算方法。

（2）锥形长药柱水下爆炸能够在起爆端一侧形成具有长脉宽特征的冲击波，通过改变长药柱的锥形参数可以调整长脉宽冲击波的峰值压力、持续时间和波形衰减规律，这为水下爆炸冲击波毁伤研究提供了一种冲击波压力波形可调的实验方法。