混凝土冲击破坏动态力学及能量特性分析*
党发宁,李玉涛,任 劼,周 玫
(西安理工大学岩土工程研究所,陕西 西安 710048)
混凝土是重大基础设施、军事防护工程中用途最广、用量最大的一种建筑材料。近年来,随着国际局势复杂、恐怖主义抬头,以及各类精确制导武器的研发使用,许多混凝土结构都面临着承受冲击、振动以及爆炸等极端外部荷载作用的威胁。这就对研究混凝土抗打击能力及结构安全性评价提出了新的要求。
动强度是评价混凝土结构物在冲击荷载作用下承载力大小的重要指标,一直是国内外学者关注的焦点问题。目前,有关动强度的探讨仍存在争议。一种观点认为随着加载速率的提高,动强度会随之提高;另一种观点认为强度是材料的固有属性,与加载速率无关。总体来看,现在普遍认同前者的观点。在受到冲击荷载作用时,混凝土破坏具有突然性、不可预估性,难以准确测量其破坏动强度,论证其破坏机理。Eibl 等从断裂力学角度出发,认为混凝土动强度提高的原因是加载速率提高导致裂纹数目增多,而形成裂纹所需的能量远高于裂纹发展所需的能量。Weerheijm认为高应变率下混凝土动强度变大是因为惯性效应,惯性力使裂纹快速扩展直接导致混凝土变形和强度增加。Rossi 等认为混凝土动强度增加主要是自由水的黏性作用(Stefan 效应)引起的。Gurusideswar 等研究发现,在冲击荷载作用下混凝土内部裂纹发育时间不足,细观裂纹和宏观裂纹的出现导致动强度增加。马怀发等以混凝土变形、损伤与时间的相关性为出发点,认为混凝土在外部荷载作用下其微细观结构发生了变形,而这种变形需要时间积累,从而导致出现损伤滞后现象,引起混凝土动强度提高。秦川等采用细观力学方法进行研究,认为在高应变率条件下,混凝土动强度提高是因为更加分散的裂纹形态与能量需求的增加。党发宁等认为材料的不均匀性(骨料率不同)使得不同速率的动裂纹发展路径不同,决定了不同速率的动强度不同。可以看出,目前虽然对混凝土的动态力学行为进行了大量探索,但尚未形成统一认识。混凝土的动强度究竟受哪些因素影响?在不同骨料率、冲击速度下动强度如何变化?这些问题仍需进一步研究。此外,也有学者认为材料在破坏过程中应力应变状态十分复杂,单纯地用应力应变曲线很难确定材料的准确强度,而材料破坏的本质是能量驱动下的一种状态失稳现象,如果可以详细分析材料破坏过程中能量的传递与转化,就有可能较为真实地反映材料的破坏规律,因而很多学者从能量角度出发描述混凝土的损伤及其它力学参数。李庆华等用应变能密度来衡量材料的韧性,认为提高材料的抗爆炸、抗冲击能力的重要途径是提高其变形能力。巫绪涛等通过对混凝土试样耗散能的分析,发现其可以有效地反映混凝土拉伸损伤性能的变化。Li 等分析了混凝土能耗密度与分形维数之间的关系,认为两者呈正相关关系。Tan 等将混凝土的耗能能力分为损伤断裂能和惯性势能,系统分析了骨料粒径、水灰比和骨料率对耗能的影响。Zhang 等、翟越等通过试验分析出混凝土试件破坏时,吸收能量的至少85%用于裂纹的扩展和发育。可以看到,现阶段在进行岩石、混凝土类材料能量耗散分析时,多采用吸收能近似代替裂纹表面能进行研究,往往忽略了裂纹表面能本身的特征,混凝土在受到冲击荷载作用破坏时,吸收能量与裂纹表面能之间转化关系如何?冲击速度、骨料含量对二者有什么影响?有关这些方面的研究鲜有报道。而对吸收能和裂纹表面能的研究,可以更加准确、全面地认识混凝土材料的变形、动强度以及能量演化规律。
基于以上分析,本文利用杆直径为100 mm 的SHPB 装置,对骨料率为0、32%、37%和42%的混凝土试样,分别进行冲击速度为5、6、7 m/s 的冲击压缩试验,以研究冲击速度和骨料率对混凝土动态抗压强度、分形维数、吸收能以及裂纹表面能的影响规律,分析吸收能与裂纹表面能之间的转化关系。拟得到动强度关于冲击速度和骨料率的函数表达式,建立裂纹表面能的相关计算公式,并对结果进行必要的分析和讨论。
1 试样制备及加载
混凝土水泥为PO32.5 普通硅酸盐水泥,粗骨料为花岗岩碎石,粒径为5 mm~20 mm,抗压强度53.6 MPa,弹性模量为67.4 GPa,泊松比为0.17。按表1 中的配合比制得骨料率分别为0%(纯砂浆)、32%、37%和42%,底部直径约100 mm,高约50 mm 的圆柱体试样,试样两底面之间的平行度相差保持在±0.02 mm 之间。冲击压缩试验在压杆直径为100 mm 的分离式霍普金森杆(split Hopkinson pressure bar,SHPB)装置上进行,如图1 所示。
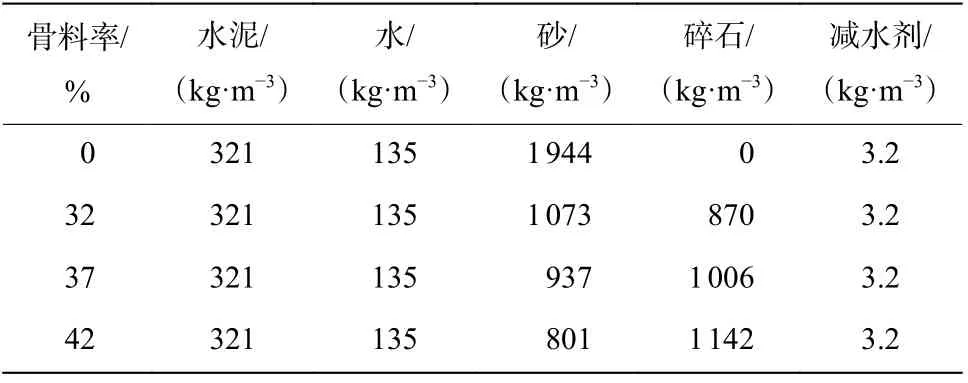
表1 混凝土配合比Table 1 Concrete mix proportions
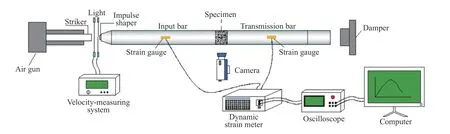
图1 SHPB 试验装置Fig. 1 SHPB test device
为解决加载过程中应力均匀性问题,减少入射波的高频震荡现象,在入射杆杆端粘贴T2 紫铜片作为波形整形器。同时,在混凝土试样两端均匀涂抹少量凡士林,以减少摩擦效应,防止不必要的干扰。通过对波形进行整形处理,试验采集的原始波形如图2 所示,可以发现入射应力波上升阶段比较平缓,上升前沿时间约为0.230 ms,作用时间维持约0.5 ms。这对减缓混凝土试样过早破坏、提高其应力均匀性起到了积极作用。对不同骨料率混凝土试样分别进行3 组不同速度(5、6、7 m/s)冲击试验,每种冲击速度下的试验重复3 次。根据SHPB 试验技术的基本假定,应力、应变和应变率为:
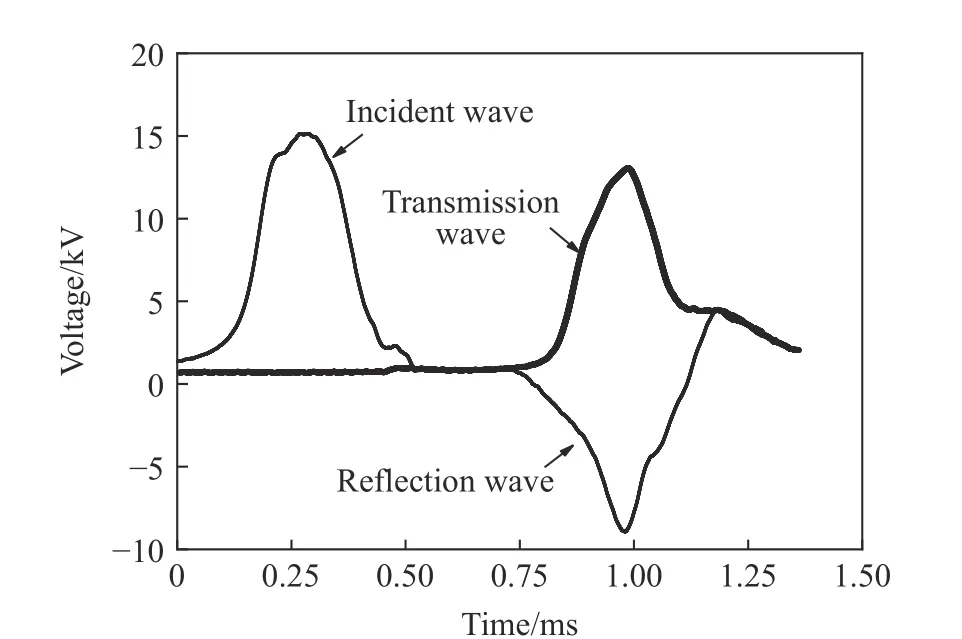
图2 SHPB 试验原始波形图Fig. 2 Primitive waveform in SHPB test

2 混凝土破坏模式及动力特性分析
2.1 混凝土试样破坏模式、破坏秩序与强度关系分析
限于篇幅原因,仅给出冲击速度为6 m/s 时不同骨料率试样动态破坏(见图3),以及骨料率为32%时不同冲击速度试样动态破坏(见图4),以研究骨料率和冲击速度对混凝土材料变形特性的影响。

图3 冲击速度不变时不同骨料率混凝土试样开裂状态Fig. 3 Cracking states of concrete specimens with different aggregate ratios at a certain impact velocity

图4 骨料率不变时不同冲击速度下混凝土试样开裂状态Fig. 4 Cracking states of concrete specimens with a fixed aggregate ratio at different impact velocities
从图3 中可以看出,当冲击速度为6 m/s 时,总是在靠近入射杆一端(试样右端)首先发现有细微的裂纹产生,随着加载的进行,裂纹沿着轴向方向开始发育、扩展直至贯穿整个试样。裂纹贯穿试样时,靠近入射杆的试样端部破坏最严重:其中当骨料率为0 时试样破坏程度最高,试样侧面有多条明显的轴向裂纹出现并伴有大量的碎块飞溅现象;当骨料为32%和37%时试样的破坏程度次之,裂纹贯穿时刻均能在试样侧面发现较明显的轴向开裂现象;当骨料率为42%时试样破坏程度最低,其侧面仅有细小的轴向裂纹。同时也可以发现,当骨料率为0、32%、37%和42%时试样裂纹起裂时刻分别为80、95、115 和125 µs;裂纹贯穿时刻分别为145、175、200 和225 µs。说明随着骨料率的增加裂纹起裂、贯穿时刻均呈增加趋势。结合图5 中所示应力-应变时程曲线进行分析,当冲击速度相同时,峰值应力随骨料率的提高而增大,应变随骨料率的提高而减小。不同骨料率混凝土起裂时刻对应的起裂应力分别为61.44、82.21、93.75 和102.46 MPa。即起裂应力随骨料率的增大而增大。混凝土试样峰值应力分别为80.36、92.48、99.36 和108.97 MPa,对应峰值应变分别为1.28%、1.09%、0.82%和0.65%,进而说明随着骨料的升高,发生破坏时混凝土动强度提高,变形减小。当骨料率为0 和32%时,起裂应力分别占峰值应力的76%和88%,而当骨料率为37%和42%时,其占比高达约94%,说明随着骨料的升高,混凝土的弹性变形能力随之提高,从而增强了混凝土的承载能力。峰值应力对应时刻分别为128.1、145.3、173.6 和188.4µs。对比试样裂纹贯穿时刻可以发现,混凝土出现了变形滞后现象,但相应的滞后间隔(16.9、29.7、26.4 和36.6 µs)随骨料率的变化没有明显的一致规律。
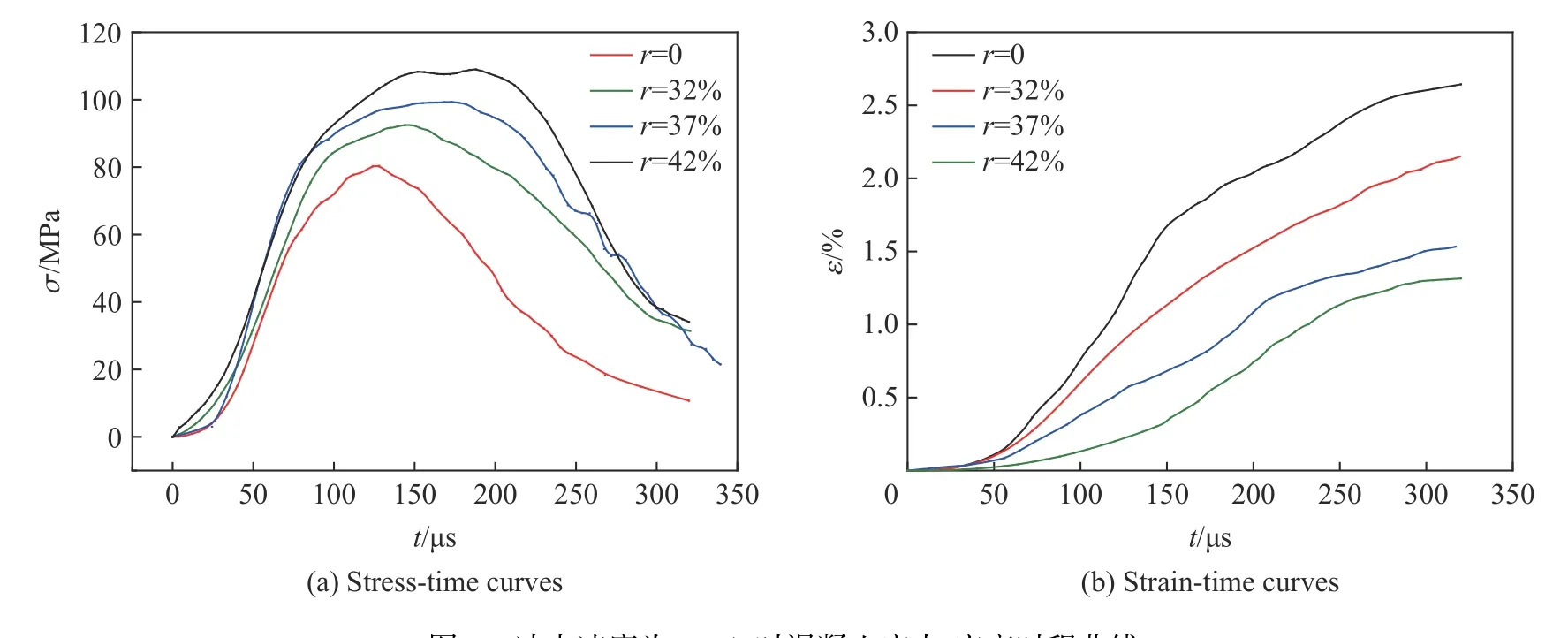
图5 冲击速度为6 m/s 时混凝土应力-应变时程曲线Fig. 5 Stress and strain history curves for concrete at an impact velocity of 6 m/s
从图4 中可以发现,随着冲击速度的增大,混凝土试样在裂纹贯穿时的轴向裂纹数目显著增多,宽度显著增大,碎块飞溅现象愈发明显。说明冲击速度越大,试样破坏越严重。结合试样受力状态、应力波传递规律和试样破坏形态分析判断,试样破坏模式主要以拉伸劈裂破坏为主。同时可以发现,当冲击速度分别为5、6 和7 m/s 时,裂纹起裂时刻分别为110、95 和55 µs;裂纹贯穿时刻分别为180、175 和145 µs,说明随着冲击速度的增大裂纹起裂、贯穿时刻均呈减小趋势。结合图6 应力、应变时程曲线进行分析,当骨料率相同时,峰值应力和应变均随冲击速度的增大而增大,应变起跳点也随冲击速度的增大有所提前,也就是说冲击速度越大,越先出现变形。不同冲击速度时混凝土起裂时刻对应的起裂应力分别为32.77、82.21 和89.35 MPa,即起裂应力随冲击速度的增大而增大。混凝土试样峰值应力分别为50.48、92.48 和105.12 MPa,对应峰值应变分别为0.26%、1.09%和1.78%。当冲击速度为5 m/s 时,起裂应力约占对应峰值应力的65%;当冲击速度为6 和7 m/s 时,起裂应力约占对应峰值应力的87%,说明冲击速度为5 m/s 时起裂应力较小,裂纹从起裂至贯穿发育迟缓,而当冲击速度为6 和7 m/s 时,起裂应力明显提高,裂纹从起裂至贯穿发育迅速,造成这种现象的原因与裂纹的扩展速度和路径等因素有关。峰值应力对应时刻分别为154.1、145.3 和90.9 µs,对比试样裂纹贯穿时刻可以发现,试样在达到峰值应力后的一段时间内才发生了贯穿断裂,出现了一定程度上的变形滞后现象,同时可以发现,随着冲击速度的增大,裂纹贯穿时刻与峰值应力时刻的间隔(25.9、29.7 和54.1 µs)呈增长趋势,即变形滞后现象愈发明显,这种滞后现象可以在一定程度上提高混凝土的承载能力。
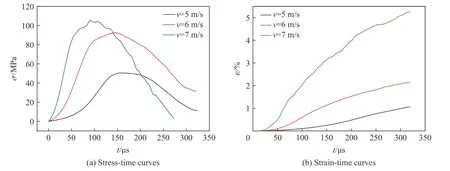
图6 骨料率为32%时混凝土应力、应变时程曲线Fig. 6 Stress- and strain- time curves for concrete at the aggregate ratio of 32%
2.2 应力-应变关系曲线分析
图7 为混凝土应力-应变关系曲线,以冲击速度为5 m/s、骨料率为32%时的应力-应变曲线为例,如图7(a),可以看出混凝土试样的动态应力-应变曲线可以分为弹性阶段()、裂纹稳定发展阶段()、裂纹非稳定发展阶段()和破坏后阶段()。在加载初期,从点开始进入弹性阶段,应变的变化缓慢应力线性增大,到达弹性极限点;随着加载的进行,从点开始进入弹塑性阶段,试样内部少许裂纹开始萌生并稳定发展至点达到屈服强度,此阶段应变持续增大,应力也迅速增大;从点开始进入塑性阶段,大量裂纹开始快速无序发展,此阶段应变快速增长,应力增长速度放缓到达峰值强度点,此时试样内部裂纹扩展、贯穿发生破坏;从点开始,进入破坏后阶段,此阶段应变继续增大应力迅速下降。另外,从图7(b)可以看出,当冲击速度不变时,随着骨料率的提高,混凝土弹性模量随之增大且弹性段增长;从图7(c)可以看出,当骨料率不变时,随着冲击速度的增大,混凝土弹性模量几乎不变仅弹性段有所增长。结合上节的分析,说明骨料率和冲击速度对混凝土强度提高的机制并不相同,骨料的增加会使混凝土的弹性模量增大,从而提升了混凝土抵抗变形的能力进而使其强度增大;而冲击速度的增大对混凝土弹性模量几乎没有影响,由冲击速度带来的惯性力及变形滞后现象更可能是混凝土动强度增大的原因。
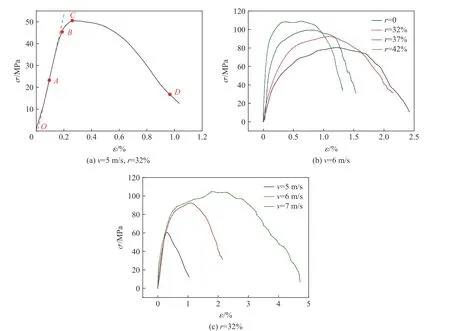
图7 混凝土应力-应变曲线Fig. 7 Stress-strain curves of concrete
2.3 动强度与骨料率、冲击速度关系分析
根据前面的分析可知,混凝土的动态抗压强度与冲击速度和骨料率含量有关。为进一步分析它们三者之间的关系,首先对不同骨料率含量的混凝土动强度与冲击速度的关系进行拟合分析。为消除骨料非均质性对混凝土强度的影响,此处取每种冲击速度下两个比较接近的动强度进行分析,如图8 所示,二者的拟合关系见表2,可以发现混凝土动强度与冲击速度均为对数形式:
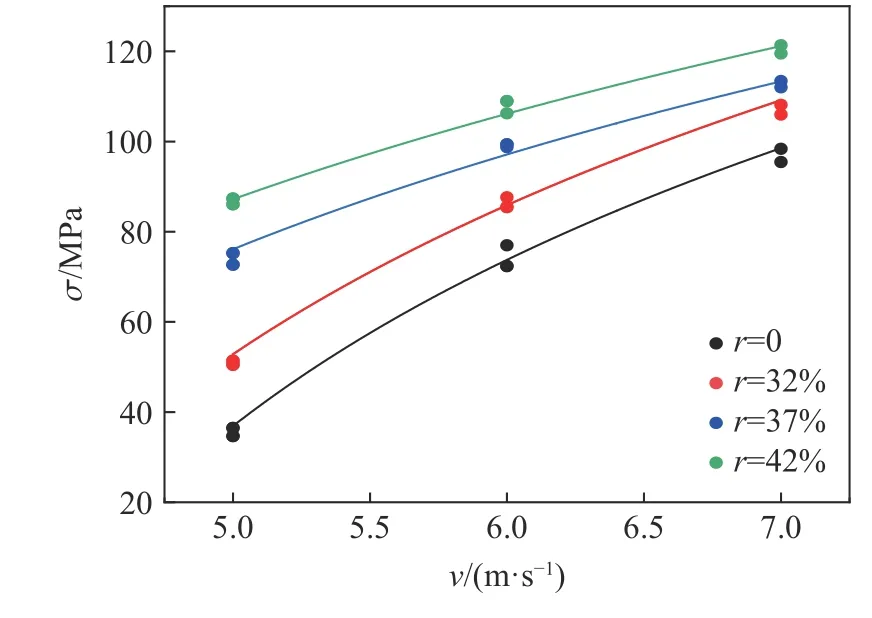
图8 混凝土动强度与冲击速度拟合关系Fig. 8 Fitting relationships between concrete dynamic strength and impact velocity

由表2 可知,拟合决定系数均在0.95 以上,表明拟合效果较佳。同时可以发现,造成式(4)中常数、不同的原因是因为骨料率含量不同,因此接下来研究、与骨料率的关系。图9 为、与骨料率的拟合曲线,可以发现、均随骨料率的增大而减小,拟合关系见式为:
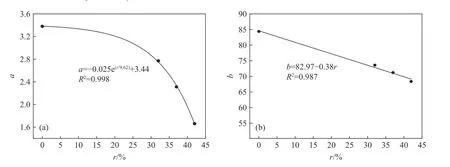
图9 骨料率与材料参数的拟合关系Fig. 9 Fitting relationships between aggregate rates and material parameters

表2 动强度与冲击速度拟合关系Table 2 Fitting relationship between dynamic strength and impact velocity


式中:σ 为混凝土动强度;、为材料参数;为骨料率;为冲击速度。
将式(5)、(6)代入式(4)便得到了动强度关于骨料率和冲击速度的函数表达式:
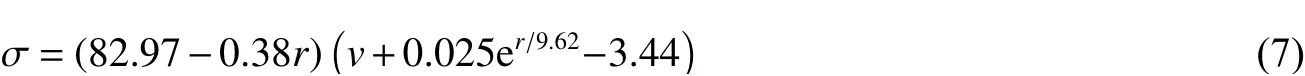
将文献[25-27]试验中相应的冲击速度和骨料率代入式(7)中进行对比分析,如图10 所示,发现用式(7)所拟合的曲线与试验实测值比较接近,证明了式(7)的适用性与可靠性。
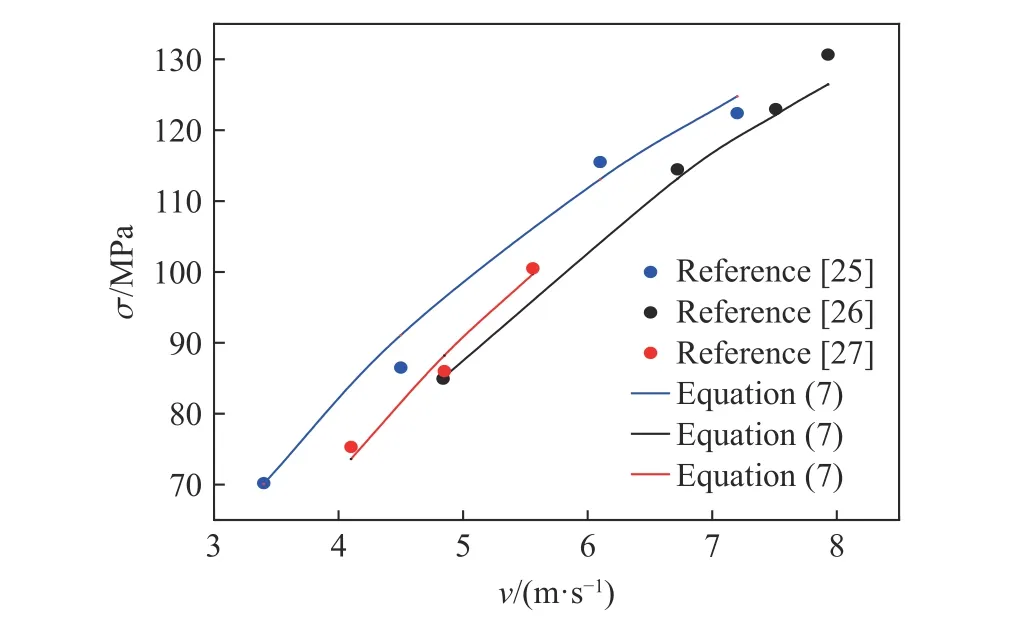
图10 混凝土动强度与冲击速度关系Fig. 10 Relationship between concrete dynamic strength and impact velocity
3 破坏碎块分形维数分析
3.1 破坏碎块分形维数计算
由于材料的宏观破坏是由小破裂群体集中而形成的,小破裂是由更微小的裂隙演化而来,这种自相似性的行为必然导致破碎后的碎块分布也具有自相似特征。由分形维数的基本概念可知,如果混凝土碎块分布具有分形特征,那么,破坏碎块分形维数的表达式如下:

式中:为碎块粒径大于的碎块数目,即筛孔径为时筛上混凝土碎块个数;为比例常数;为混凝土破坏碎块分形维数。
碎块的质量-频率分布方程为:
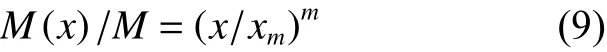
式中:() 为混凝土碎块粒径小于的累计质量;为混凝土碎块总质量;为混凝土碎块最大粒径;为比例常数。
对式(8)、(9) 分别求导得:d∝d,d∝xd;同时增加碎块数目必然引起质量的增加,即d∝d;于是得∝x,从而得到:

以冲击速度为7 m/s 时不同骨料率混凝土破坏碎块分形维数计算曲线为例,如图11 所示,从图中可以发现拟合直线的相关性较高,表明混凝土冲击破碎后的碎块分布符合分形规律。
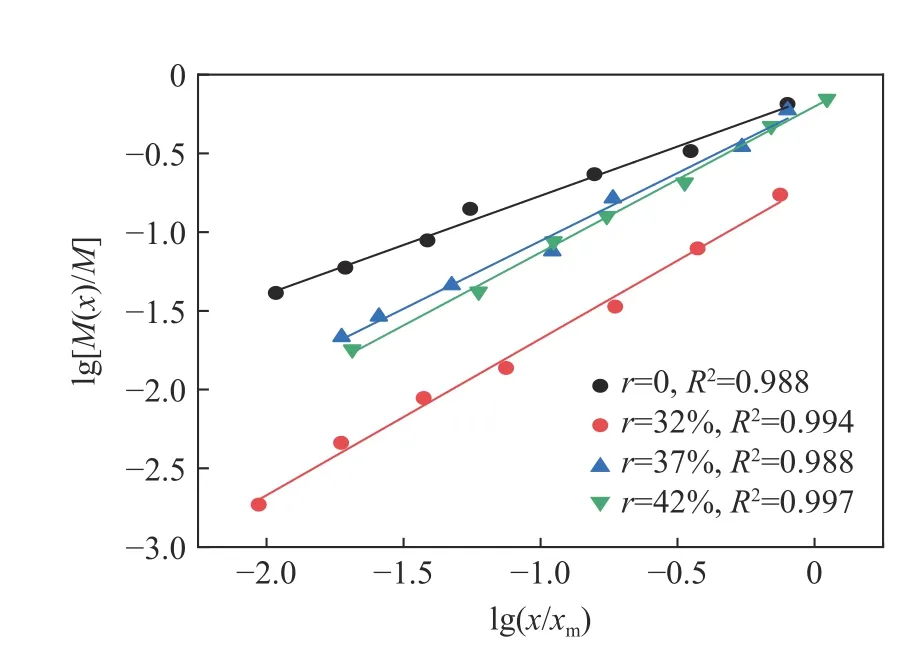
图11 分形维数双对数曲线Fig. 11 Double logarithmic curves of fractal dimension
3.2 破坏碎块分形维数与冲击速度、骨料率
冲击速度与混凝土破坏碎块分形维数关系如图12(a)所示。从图中可以看出,不同骨料率混凝土试样其破坏碎块分形维数均随冲击速度的增大而增大,呈线性正相关关系。以骨料率为32%的混凝土试样为例,对比混凝土破坏形态与冲击速度、破坏碎块分形维数关系(见图13)可以发现,加载速率越低,碎块数目少且粒径较大,破碎程度较低,混凝土破坏碎块分形维数越小;加载速率越高,碎块数目多且粒径较小,破碎程度较高,混凝土破坏碎块分形维数越大。这是因为不同冲击速度作用下混凝土试样内部裂纹的发展路径不同,当冲击速度较小时,裂纹会绕着骨料发育,混凝土试样破坏程度较低,破坏碎块分形维数较小;当冲击速度较大时,裂纹会直接穿越骨料发展,混凝土试样破坏彻底,破坏碎块分形维数更大。破坏碎块分形维数与骨料率的关系如图12(b)所示。从图中可以看出,相同冲击速度下,破坏碎块分形维数随骨料率的增加而减小,呈线性负相关关系。相同冲击速度下,骨料率为0 时破坏碎块分形维数最大,骨料率为42%时破坏碎块分形维数最小;骨料率从0 过渡到32%时,破坏碎块分形维数明显减小,约减小了8%。因为混凝土在冲击压缩过程中内部骨料会形成稳定的骨架结构,在一定程度上可以阻碍和抑制裂纹的发育、扩展,有利于保护混凝土试样的结构整体性,从而提高混凝土的抗冲击能力。在受到相同冲击作用时,无骨料混凝土试样已经发生整体碎裂破坏,而有骨料试样因其骨架结构作用只发生了局部断裂破坏,从而导致无骨料试样和有骨料试样破坏后破坏碎块分形维数变化幅度较大。另外,也可以发现,每种冲击速度下重复的3 次试验的分形维数大多数都比较接近,只有极个别组数据离散性大,说明骨料非均质性对分形维数的影响不大。
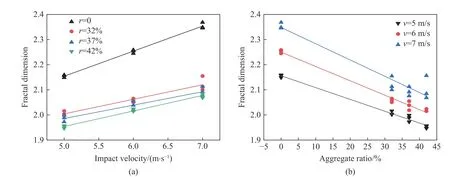
图12 冲击速度、骨料率与分形维数关系Fig. 12 Relationships between impact velocity, aggregate ratio and fractal dimension

图13 不同冲击速度以及分形维数下的混凝土破坏形态Fig. 13 Concrete failure morphology at different impact speeds and fractal dimensions
3.3 破坏碎块分形维数与碎块表面积
混凝土试样冲击破坏后碎块的比表面积与其受荷时吸收的能量以及静、动强度的大小有关,研究破坏碎块的比表面积有利于从断裂力学角度揭示混凝土动强度的提高机理。混凝土试样发生破坏时,其碎块粒径大小不一且表面凹凸不平,因此,很难有效地统计试样破坏后碎块的总表面积。为便于统计,计算混凝土碎块表面积时,当碎块粒径大于20 mm 且具有一定的形状特征时,按照碎块的特征形状进行计算。当碎块形状类似于圆锥形或圆柱形时,按相应的表面积计算公式计算碎块的理想表面积;当碎块粒径小于20 mm 时,将混凝土碎块等效成球体,球体直径取各层筛上混凝土碎块平均粒径,这样可以计算得到混凝土碎块的理想表面积。而混凝土试样由于骨料率以及所受冲击荷载不同,冲击后的碎块表面粗糙程度也不尽相同,而裂纹的发育、扩展路径不同是造成碎块表面粗糙度不同的直接原因,破坏碎块分形维数是试样内部裂纹扩展、演化的宏观反映,赵昕等的研究也表明混凝土碎块断裂面粗糙度与破坏碎块分形维数有一定关系,所以可以用破坏碎块分形维数表征试样破坏时碎块的粗糙程度。那么,混凝土受冲击压缩作用后,碎块的新增表面积可以用下式进行计算:

式中:为碎块理想统计表面积;为试样原有表面积;为碎块实际新增表面积。
4 能耗特性分析
4.1 能量计算
SHPB 试验加载过程中,入射波、反射波和透射波所携带的能量、和可分别表示为:


由前面混凝土破坏模式分析可知,试样在受到冲击压缩荷载作用时主要以拉伸劈裂破坏为主,为了得到试样冲击压缩作用下裂纹表面能,必须知道试样在劈裂拉伸状态下形成单位裂纹面积所需能量。为此,对不同骨料率混凝土试样进行了SHPB 劈裂拉伸试验,由于单位裂纹表面能是材料的固有属性,所以对每组试样只进行冲击速度为4 m/s 的劈裂拉伸试验并统计劈裂拉伸破坏后碎块的表面积。根据平琦等的研究可知,在SHPB 劈裂拉伸试验中,占的约95%,所以在加载速率较低情况下用近似代替,以此计算出劈裂拉伸状态下混凝土形成单位裂纹面积所需能量,结果如表3 所示,表中T 代表劈裂拉伸试验。
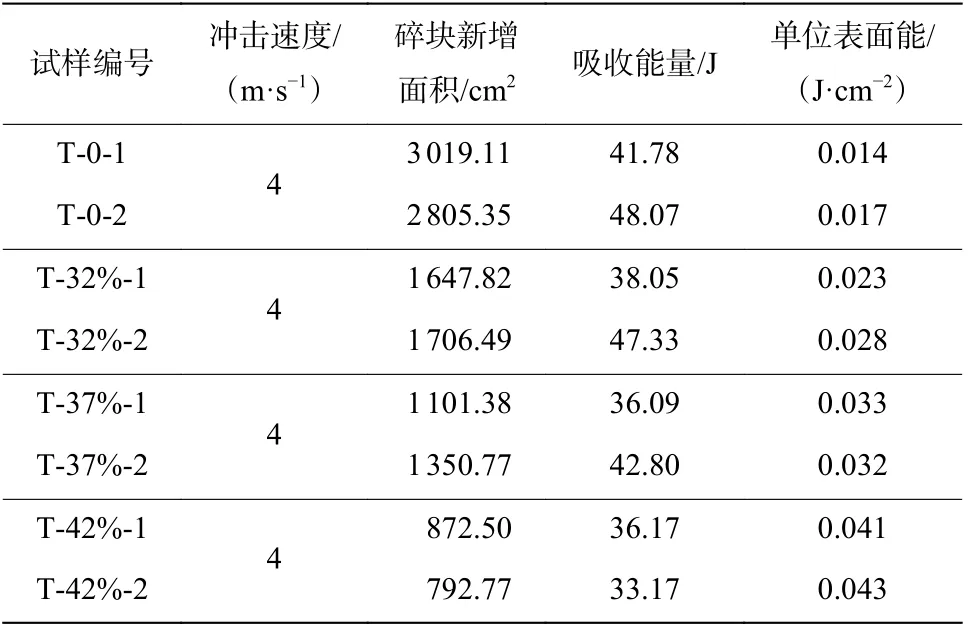
表3 单位表面能计算结果Table 3 Calculation results of specific surface energy
根据表3 所得结果,分别取两组劈裂拉伸试样单位裂纹表面能均值,作为其对应骨料率混凝土试样在冲击压缩作用下形成单位裂纹面所需表面能,联立式(11)和式(15)即可求得新形成裂纹面所需能量,即分形维数与裂纹表面能的关系式:

4.2 试样吸能与裂纹表面能
图14 为不同冲击速度下,试样吸收能、裂纹表面能随骨料率变化的关系曲线。可以发现,相同冲击速度下试样吸能和裂纹表面能均随骨料率的增加而降低,因为当冲击速度一定时,入射能的大小基本保持不变,反射能和透射能随着混凝土试样骨料率的变化而变化,当骨料率增加时,试样的平均密度和弹性模量会相应提高,试样在受到冲击荷载作用时更不易发生破坏,有利于保护混凝土试样的整体性,试样的整体性越好,波阻抗越大,则入射应力波在试样表面处的反射系数将减小,透射系数将增大,最终导致混凝土试样的反射能减小,透射能增大,吸收能总体呈减小趋势。同时,骨料会在一定程度上提高混凝土试样的抗压和抗拉强度,使得试样的破坏程度降低,混凝土碎块总面积减少,虽然随着骨料率的增加单位表面能也随之增加,但是单位表面能的相对增加量远不及碎块总表面积的相对减少量,所以裂纹表面能随骨料率的增加呈减小趋势。
图15 所示为不同骨料率混凝土试样吸收能、裂纹表面能随冲击速度变化的关系曲线,从图中可以看出,二者的变化规律基本一致,即试样吸收能和裂纹表面能均随着冲击速度的增加而增加。因为随着冲击速度的增加,入射能随之增加,试样破坏程度加重,导致混凝土试样与压杆波阻抗出现严重不匹配现象,使得入射波只能在初始应力均匀过程中向透射杆传递透射波,一旦试样发生破坏,将不再产生或只产生少量透射波,入射波大部分会以反射波的形式反射回入射杆中,而反射能的增量相对于入射能增量来说很小,由式(13)可以知道吸收能总体呈增加趋势;混凝土试样破坏程度越严重,产生的碎块越多,相应的裂纹表面积就越大,对于同种骨料率的试样来说,由于其单位裂纹表面能是恒定的,那么,碎块表面积越大,则裂纹表面能越大。此外,也可以看出,试样吸收能始终高于裂纹表面能,因为受到冲击作用时,试样吸收的能量不仅用于裂纹扩展形成裂纹表面能,还有一部分能量以碎块飞溅能、电磁能、热能等形式耗散于外部环境中。
从图14 和图15 中还可看出试样吸收能与裂纹表面能的关系。首先,两者变化规律的一致性很好,均随骨料率的增加而减少。其次,均随冲击速度的提高而提高,这是由于随冲击速度的提高混凝土碎块总表面积不断增大。其三,试样吸收能与裂纹表面能的差值随冲击速度的提高而增大,也就是冲击速度较小时,两者的差值较小,尤其是在准静态加载时试样吸收能基本全部转化为裂纹表面能,飞溅出去的碎块动能以及以其他形式消耗的能量可以忽略不计,而随着冲击速度的增加,以及所占比例增大,试样吸收能与裂纹表面能的差值随之增大。

图14 试样吸收能、裂纹表面能与骨料率关系Fig. 14 Relationships of absorbed energy and crack surface energy of the specimens with aggregate ratio
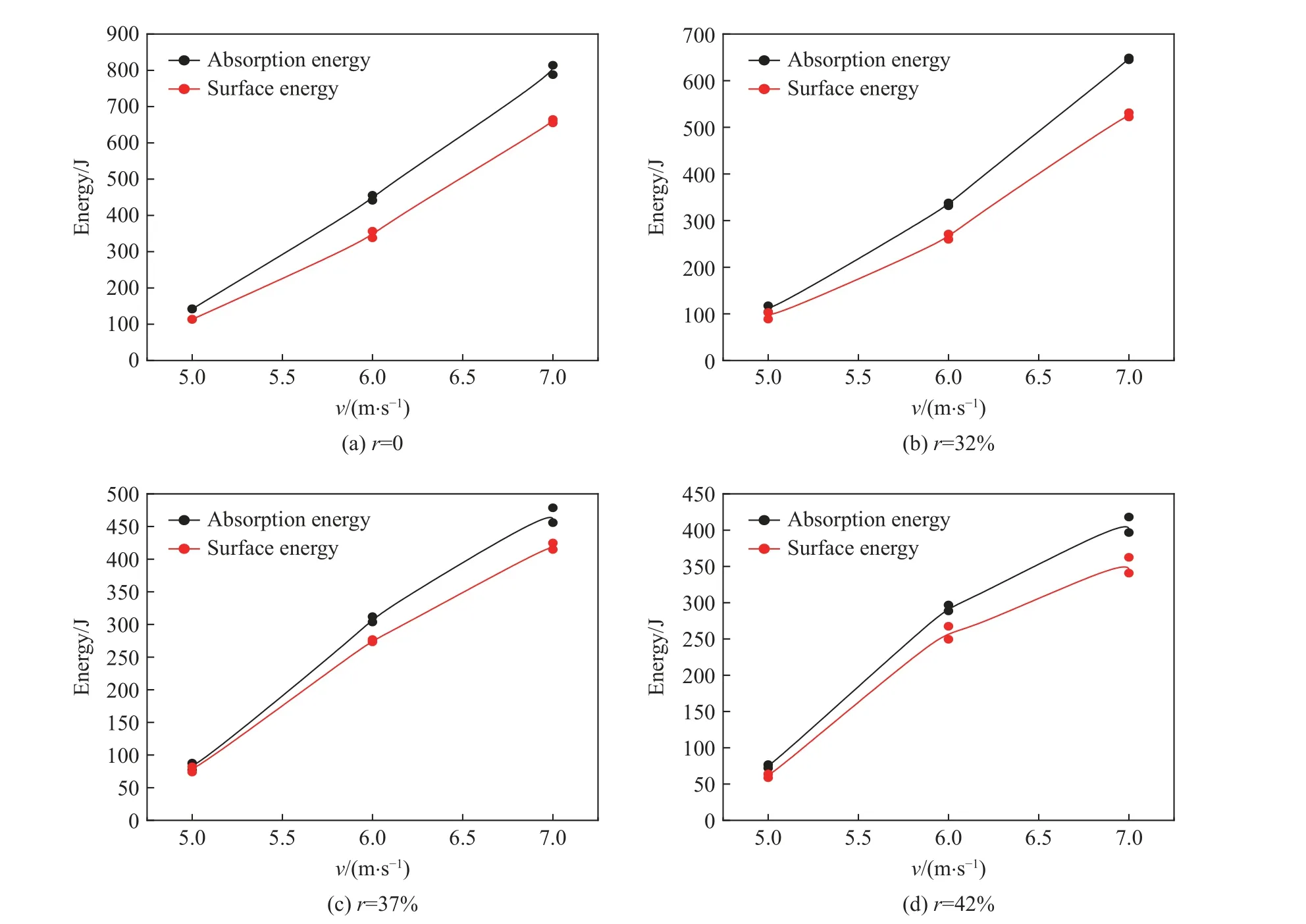
图15 试样吸收能、裂纹表面能与冲击速度关系Fig. 15 Relationships of absorbed energy and crack surface energy of the specimens with impact velocity
4.3 试样吸收能转化率
为进一步研究试样吸收能与裂纹表面能之间的关系,有必要对两者之间的差异进行分析。定义混凝土试样吸收能转化率α 为试样裂纹表面能与吸收能之比,即:

图16 所示为冲击速度与α 的关系,可以看到,当骨料率一定时,α 随冲击速度的改变变化幅度较小,骨料率为0 时,α 在0.77~0.83 之间变化,均值为0.80;骨料率为32%时,α 在0.78~0.88 之间变化,均值为0.83;骨料率为37% 时,α 在0.88~0.96 之间变化,均值为0.91;骨料率为42%时,α 在0.86~0.90 之间变化,均值为0.88。说明α 受冲击速度影响较小而受骨料率的影响较大,也可以认为α 是混凝土材料的固有属性,不会因冲击速度的变化而发生较大变化,但是骨料率的改变却会很大程度上影响α。同时也可以看到,并不是骨料率越大α 值越大,就本次试验而言,骨料率为37%时α 最大,值为91%,即该骨料率的混凝土试样在受到冲击荷载作用时,其吸收能量的91%用于裂纹的扩展和发育,转化为裂纹表面能。
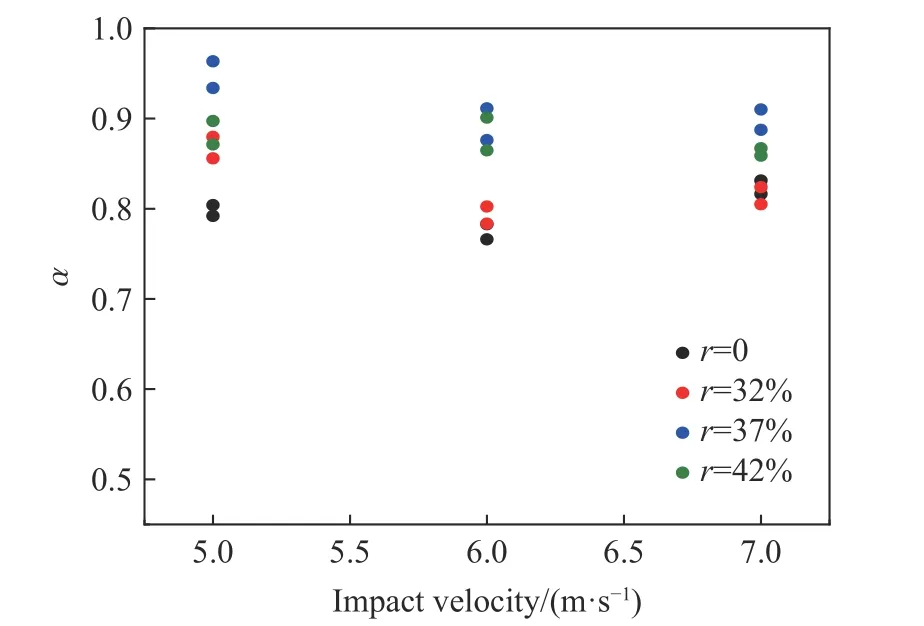
图16 冲击速度与α 关系Fig. 16 Relationship between impact velocity and α
5 结 论
利用SHPB 试验装置对骨料率为0、32%、37% 和42% 的混凝土试样,依次进行了速度为5、6、7 m/s 的冲击压缩试验。主要得出以下几条结论。
(1)混凝土试样在受到冲击荷载作用时,靠近入射端的试样一侧首先出现裂纹,随着加载的进行,沿试样侧面轴向有细小的裂纹产生并伴随着轻微的碎块剥落现象,随后裂纹继续沿着轴向发育、扩展,直至贯穿整个试样。结合试样受力状态、应力波传递规律和破坏形态分析判断,试样破坏以拉伸劈裂破坏为主。
(2)混凝土动强度的提高是骨料率和冲击速度的耦合作用结果,骨料的增加提高了混凝土的弹性模量,进而提高了动强度;冲击速度产生的惯性力以及变形滞后现象使混凝土动强度得以提高。建立了动强度关于骨料率和冲击速度的表达式,通过与其他文献数据对比验证了其适用性和可靠性。
(3)加载速率低,混凝土碎块数目少且粒径较大,破碎程度低,破坏碎块分形维数小;加载速率高,混凝土碎块数目多且粒径较小,破碎程度高,破坏碎块分形维数大;相同冲击速度下,破坏碎块分形维数随骨料率的增加而减小。
(4)破坏碎块分形维数不仅可以描述混凝土的破坏程度,也可以较好地表征碎块表面粗糙程度,建立了裂纹表面能、吸收能和破坏碎块分形维数之间的关系表达式。试样吸收能和裂纹表面能随冲击速度的增加而增加,随骨料率的增加而降低,吸收能始终高于裂纹表面能,且随着骨料率的增加二者的差异逐渐减小,随冲击速度的增加,二者的差异逐渐增大。
(5)可以认为吸收能转化率α 是混凝土材料的固有属性,对同一骨料率而言,α 随冲击速度的改变变化不大;当骨料率不同时,α 的变化幅度较大;但并不是骨料率越大,α 的值越大,就本次试验而言,当骨料率为37%时α 最大,为91%,即约91%的吸收能转化为裂纹表面能。

