一类带组合非线性项波动方程解的破裂

张文君，韩伟，明森，杜嘉仪

（中北大学理学院，山西 太原 030051）

0 引言及主要结论

随着现代科学技术的飞速发展，偏微分方程作为一门重要的学科被广泛应用于诸多领域。波动方程是偏微分方程的重要分支，常被用于研究波的传播及弦的微小振动等物理现象。波动方程是一类典型的双曲型方程，具有重要的物理背景、理论意义和应用价值。波动方程已成为非线性发展方程研究的热点问题之一，非线性波动方程的稳定性理论、散射理论及其破裂性态的研究可以更好地揭示波的传播规律等。由于非线性项的影响，波在传播过程中会变得陡峭直到破裂。由于现实中存在摩擦现象，因而阻尼等因素会影响物理系统的能量，结合非线性外力作用会影响解的破裂性态与生命跨度估计。然而，由于阻尼项系数依赖于时间变量，从而会对物理系统的能量以及振幅产生更为复杂的影响。因此，本文研究带阻尼项波动方程解的破裂性态，更深刻和全面地认识波传播理论中的物理现象，为数值模拟和实际应用提供理论支撑，具有重要的意义。

近来，许多数学工作者对波动方程的解的破裂及其生命跨度的上界估计与非线性项指数和空间维数的关系进行了大量的研究［1-20］。Strauss W A［1］得到波动方程utt-Δu=|u|p的初值问题具有Strauss临界指数pc(n)。当n≥2时，pc(n)是二次方程

的正根；当1＜p≤pc(n)时，问题的解会在有限时间内破裂；当p＞pc(n)时，问题存在整体解。文献［2］研究了变系数波动方程的初边值问题，其中非线性项为|u|p。文献［4］研究了带导数非线性项的波动方程ut-Δu=a2|ut|p+b2|∇u|p(a2+b2＞0)具有Glassey临界指数pG(n)=1+2(n-1)。文献［5］在n维全空间中研究了次临界指数带散射阻尼项μ(1+t)-βut(β＞1)的波动方程，其中非线性项为|u|p。文献［6］研究了带散射阻尼项与尺度不变阻尼项的波动方程，其中非线性项为|ut|p。文献［7］在次临界指数时研究了带散射阻尼项与组合非线性项的波动方程。利用检验函数方法和迭代方法得到解的生命跨度的上界估计。文献［12］研究了带散射阻尼项和负质量项的波动方程，得到解的生命跨度的上界估计。文献［18］在Rn中研究了半线性波动方程耦合系统解的破裂。

本文在外区域上研究如下变系数波动方程的初边值问题

其 中μ＞0，β＞1，Ωc=RnB1(0)。supp(f，g)⊂BR(0)∩Ωc，其 中BR(0)={x||x|≤R}，R＞2。f(x)，g(x)≥0且f(x)，g(x)不恒等于0。A(x)={aij(x)}n i，j=1表示光滑实对称n×n矩阵，并且存在正常数C使得C-1|ξ|2≤aij(x)ξi ξj≤C|ξ|2，∀ξ∈Rn，x∈Ωc。此处采用爱因斯坦记号，重复指标i，j表示求和。当|x|＞R＞2时，aij(x)=δij，其中δij为Kroneckerδ函数。V(x)表示位势。

本文拟结合文献［7，12］，在外区域上研究变系数问题（1）。主要结果如下。

定理1设n≥1，V(x)＞0，且V(x)≤C(1+|x|2+δ)-1，C＞0，δ＞0均为常数。aij(x)=δij。假设问题（1）的解满足suppu⊂{(x，t)∈Ωc×[0，T)||x|≤t+R}。若p＞1且

则解u会在有限时间内破裂，且生命跨度T(ε)的上界估计为T(ε)≤Cε-2p()q-1[2q+2-(n-1)p(q-1)]，其 中C是与ε无关的正常数。

定理2设n≥2，V(x)＞0，且V(x)≤C(1+|x|2+δ)-1，C＞0，δ＞0均为常数。aij(x)=δij。设问题（1）的解满足与定理1相同的条件。当p＞2n(n-1)，1＜q＜(n+1)(n-1)时，解u会在有限时间内破裂，且生命跨度T(ε)的上界估计为

定理3设n≥1，V(x)＞0，且V(x)≤C(1+|x|2+δ)-1，C＞0，δ＞0均为常数。aij(x)=δij。假设问题（1）的解满足与定理1相同的条件。则解的生命跨度上界估计为

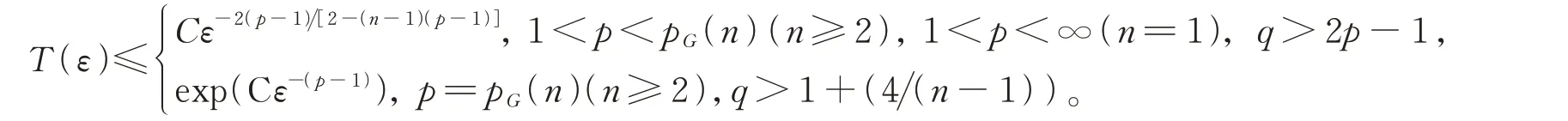
定理4设n=1时p＞1，n≥2时1＜p＜pG(n)，V(x)≤-K0，其中K0＞0。若问题（1）的解满足与定理1相同的条件，则解u会在有限时间内破裂，且生命跨度的上界估计为T(ε)≤Cε-2p(p-1)r(p，n)。

注1当V(x)=0时，问题（1）为带散射阻尼项的变系数波动方程的初边值问题。类似于文献［7］的证明过程，可知定理1-3的结论仍成立。

注2文献［5-6］在全空间中研究波动方程的初值问题，其中非线性项分别为|u|p，|ut|p。本文在外区域上研究带组合非线性项的变系数问题（1）。通过构造乘子，利用检验函数方法与迭代方法，得到问题（1）解的生命跨度的上界估计。当V(x)＞0时将文献［7］中研究的问题推广至外区域上带位势项的变系数问题。当V(x)=0时将文献［7］研究的问题推广至外区域上变系数问题。当V(x)≤-K0时将文献［12］中研究的问题推广至外区域上带负位势项的变系数问题。

1 一些引理

引理1［3］当V(x)≥0时，存在检验函数φ0(x)，φ1(x)∈C2(Ωc)满足

其中C0，C1为正常数。特别地，当V(x)=0时，有

现记ψ(x，t)=e-tφ1(x)，其中φ1(x)如引理1中所述。

引理2［2］设p＞1，φ0(x)与φ1(x)满足引理1中的条件。则∀t≥0，有

其中C为正常数。

令m(t)=exp(μ(1+t)1-β(1-β)，则有m(0)≤m(t)≤1。

引理3［7］设ψ(x，t)满足引理，u是问题（1）在[0，T)上的弱解。记

则对∀t≥0，有

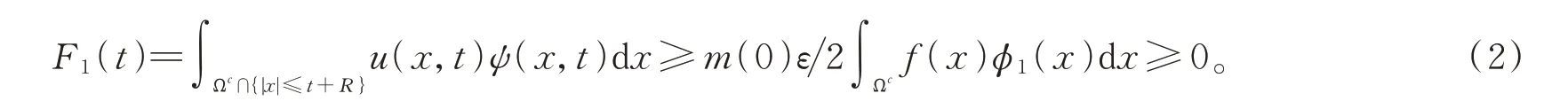
引理4［2］设φ0(x)，φ1(x)满足引理1中的条件，并且

其中φ0(x)满足x∈Ωc，0＜φ0(x)＜1。

并且存在常数C1＞0，使得0＜φ1(x)≤C1(1+|x|)-(n-1)2e|x|，∀x∈Ωc。

引理5［7］设ψ(x，t)满足引理1所述，u是问题（1）在[0，T)上的弱解。记

则对∀t≥0，有

首先，给出问题（1）的弱解的定义。

定义1当V(x)＞0，aij=δij时，问题（1）的弱解满足

并且

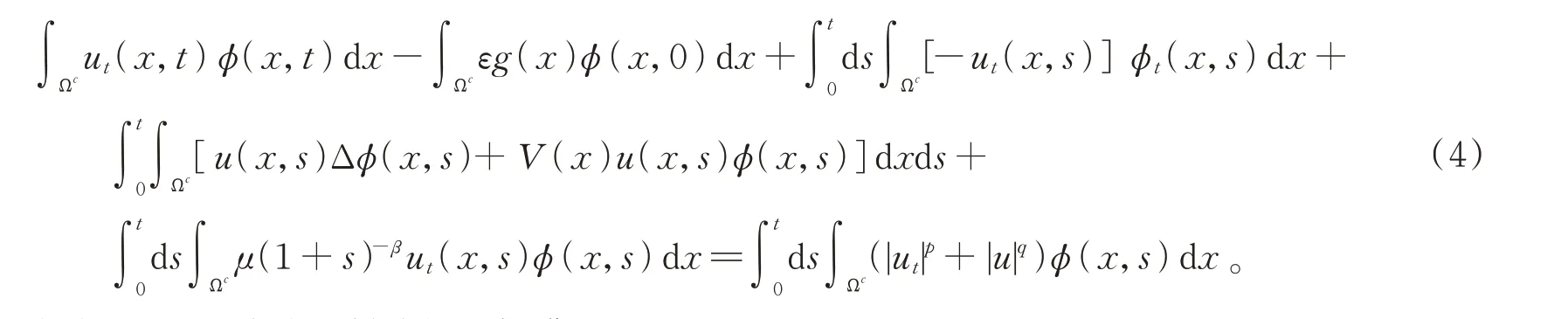
定义2当V(x)≤-K0时，问题（1）的弱解满足

并且

其中φ∈C∞0(Ωc×[0，T))，t∈[0，T)。

2 定理1的证明

引入如下函数

其中u是问题（1）在[0，T)上的解，φ1(x)如引理1所述，ψ(x，t)=φ1(x)e-t。

当V(x)＞0时，利用aij(x)=δij，在式（1）两边同乘以φ0(x)，并积分计算可知

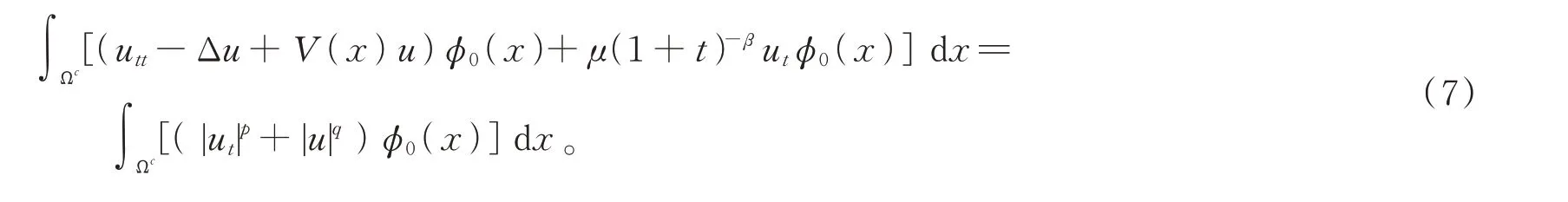
由引理1可得

从而

下面建立F0(t)的估计。

在式（4）中令φ(x，s)=φ0(x)，其中|x|≤s+R，结合引理1和式（8），得到

两边同乘以m(t)，利用F0(0)＞0，F′0(0)≥0，m(0)≤m(t)≤1，则∀t≥0，计算可得

类似于文献［7］中的计算，可知F1(t)的估计满足引理3中的式（2）。

下面建立F2(t)的估计。

由引理2，引理5以及Hölder不等式得

其中C3=m(0)C2[n(n+1)]。利用Hölder不等式可知

下面利用迭代方法建立问题（1）解的生命跨度T(ε)的上界估计。假设F0(t)满足

且D1=C3εp，a1=(n-1)p2，b1=n+1。将式（12）代入式（11）得到

当t≥1时，J(t)≥log(D1t1+2(q-1)-(n-1)p2)-C6，C6=((n-1)p2+n)log 2+Sq(∞)。所以若t≥，则有J(t)≥1。在式（14）中令j→∞，可知F0(t)→∞，从而得到定理1中生命跨度的上界估计。定理1证毕。

3 定理2-3的证明

定理2的证明根据式（9）可得

利用1＜q＜(n+1)(n-1)，可得定理2中生命跨度的上界估计。定理2证毕。

定理3的证明结合文献［6］和定理1的证明，令

根据m(0)≤m(t)≤1可知，m1-p(t)≥1。利用引理2，结合G(t)＞0，得到

其中H(0)=(m(0)C0，g2)ε＞0。通过求解常微分不等式（17），即得定理3中的生命跨度估计。定理3证毕。

4 定理4的证明

首先建立F0(t)的估计。当V(x)≤-K0时，在式（5）中令φ(x，s)=φ0(x)，由引理4得到

利用V(x)≤-K0，在式（18）两边关于t求导，计算得到

在式（19）两边同乘以m(t)，并在[0，t]上积分可得

类似于文献［12］中的分析，可得F0(t)＞0，进而得到F′0(t)≥0。

下面建立F1(t)的估计。对式（5）求导并且两边同乘以m(t)并在[0，t]上积分，可知

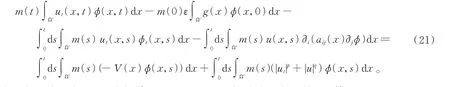
在式（21）中令φ(x，t)=ψ(x，t)=e-tφ1(t)，则φt=-φ，φtt=∂i(aij(x)∂jφ(x，s))。于是

计算得到

从而F1(t)＞(1-e-2)2m(0)Cf，0ε，t≥1。根据引理2，引理5及式（9）得到式（11）。

类似于利用迭代方法证明定理1的过程，即可得到定理4中解的生命跨度估计，此处略之。定理4证毕。