有限时间未知观测器的欠驱动轨迹跟踪控制*

郭亚楠，肖 菡，宋 帆

（1.许昌电气职业学院，河南 许昌 461000；2.郑州大学软件与应用科技学院，郑州 450000）

0 引言

欠驱动指的是控制量数目小于系统自由度数量，欠驱动系统已经在工业生产生活中越来越普遍。其中，欠驱动地面车辆的轨迹跟踪控制已经成为一个热点研究方向。如何实现欠驱动地面车辆的轨迹跟踪控制将对航空航天技术、车辆控制领域以及航海领域均具有重要的意义。针对欠驱动系统，已经产生了一系列研究，见文献［4-11］。

本文提出了一种基于有限时间未知观测器的欠驱动水面艇交互式轨迹跟踪控制（FUO-based interactive trajectory tracking control，FUO-ITTC）。有限时间未知观测器（FUO）可以在短时间内精确识别未知项，并且通过复合坐标变换（composite coordinate transformation，CCT）来建立解耦轨迹跟踪误差动力学，采用高阶滑模技术设计了FUO，实现了对复杂未知量的精确观测。实验结果证明了提出方法的有效性。

1 问题描述

本文考虑一种配备有两个螺旋桨的USV，这两个螺旋桨通常是前后不对称的，非对称欠驱动水面艇（AUSV）的运动学和动力学可以描述如下：

式（8）中所需的偏航动力学涵盖了一大类典型轨迹，包括直线、圆和渐开线螺旋，从而完全消除了要求的持续激励条件。

2 复合坐标变换

由于惯性不对称和系统式（1）和式（3）固有的欠驱动约束，需要一系列坐标变换来解耦摇摆和偏航动力学。在序列中设计了CCT，定义复合运动学和动力学跟踪误差，如下所示：

3 控制器设计与稳定性分析

3.1 有限时间未知观测器

3.2 偏航控制

在整个控制方案中，基于由式（15）～ 式（22）控制的FUO 的偏航控制器在第一步合成如下：

是全局一致渐近稳定，证明结束。

3.3 喘振控制

考虑∑系统（28）的标准形式如下：

使用式（15）和式（22）中的FUO 设计喘振控制器，如下所示：

交互摇摆和偏航动力学：

定理3：使用基于FUO 的喘振控制式（36），以及交互动力学式（37）和式（38），闭环∑系统如下：

是全局渐近稳定的。

证明：加上式（35）和式（39），可以得到

考虑Lyapunov 函数如下：

系统（42）对于V的微分：

将式（36）～ 式（38）和式（40）代入式（44）中，通过定理1，可以得到：

4 级联结构

在这种情况下，可以确保整个闭环系统式（49）的全局渐近稳定性。

定理4：方案（33）和（36）可以全局渐近地跟踪AUSV（1）到（3）所控制的期望轨迹，具有交互动力学（37）和（38），即整个闭环跟踪误差系统（49）是全局渐近稳定的。

证明：由定理2 和3，需要检查是否满足非线性上的线性G增长条件。从式（40），可以得出

式中，

5 仿真研究与比较

表1 主要参数

表2 FUO-ITTC 的用户定义参数

5.1 非零常数期望横摆角速度

5.2 零期望横摆角速度

如图1（b）所示，直线轨迹由具有恒定期望航向的虚拟AUSV 交互生成，即零期望横摆角速度r=0。图1（b）所示的轨迹跟踪结果表明，所提出的FUOITTC 方案即使在复杂未知情况下也能够使AUSV精确地跟踪直线轨迹。如图3（a）所示，可以同时精确地实现位置跟踪和姿态保持。此外，图3（b）所示的喘振、摇摆和偏航动力学的跟踪误差也可以通过图3（c）所示的基于FUO 的喘振和偏航控制输入，使其全局渐近稳定。另外，除了交互摇摆行为外，动力学和动力学的显著跟踪性能还得益于对复杂未知项的精确观测，如图3（d）所示。

图1 交互式轨迹跟踪性能

图2 非零常数DYR 情形的仿真结果

图3 零动态情况下的仿真结果

5.3 渐开线螺旋轨迹

如图1（c）所示，虚拟AUSV 交互生成具有渐近期望横摆角速度的渐开线螺旋轨迹，并可使用FUO-ITTC 方案由AUSV 精确跟踪。因此，可以同时使用图4（a）所示的渐近跟踪误差动力学来精确跟踪所需的位置和方向。此外，如图4（b）所示，所需的平移和旋转速度也可以精确跟踪。由于期望横摆角速度渐近收敛到非零常数，如图4（c）所示，AUSV 要求增加偏航控制扭矩，以确保所需航向能够被跟踪，而喘振控制输入同时为喘振和摇摆动力学提供力。在这种复杂情况下，除了基于FUO 的复杂未知的精确识别外，还可以跟踪渐开线螺旋控制扭矩，以确保所需航向的跟踪，而喘振控制输入同时为喘振和摇摆动力学提供力。结合图4（d）所示的基于FUO 的复杂未知量精确辨识，在这种复杂情况下，具有复杂未知量的AUSV 可以通过速度跟踪精确跟踪渐开线螺旋轨迹。

图4 渐近DYR 情形的仿真结果

5.4 性能比较

此外，为了定量地证明FUO-ITTC 框架的优越性，本节分别对积分绝对误差（IAE）和积分时间加权绝对误差（ITAE）指标测量的瞬态和稳态轨迹跟踪性能进行了比较。当交互动力学和FUO 技术都从本文框架中移除时，FUO-ITTC 方法将退化为所谓的级联反推（CB）方法。在本文中，通过通用用户定义参数，可以与CB 方法及其基于FUO 的变体（FUO-CB）进行比较。实际上，由于所提出的CCT方法，CB 方法不能处理非对称惯性质量，因此，CB方法适用于AUSV。下页表3 和表4 分别总结了非零常数、零动态和渐近动态的性能比较结果，从中可以看出，FUO-ITTC 方法在IAE 和ITAE 度量方面都达到了最高的轨迹跟踪精度，而FUO-CB 和CB方法在所有情况下都明显低于FUO-ITTC 和ITTC（其中不使用FUO）方法。在这种情况下，ITTC 方法的优越性可以从瞬态和稳态性能两方面得以证明。此外，可以观察到，无论ITTC 和CB 方法如何，FUO都能准确地识别复杂的未知量，从而在提高轨迹跟踪性能方面起到关键作用。

表3 轨迹跟踪性能比较

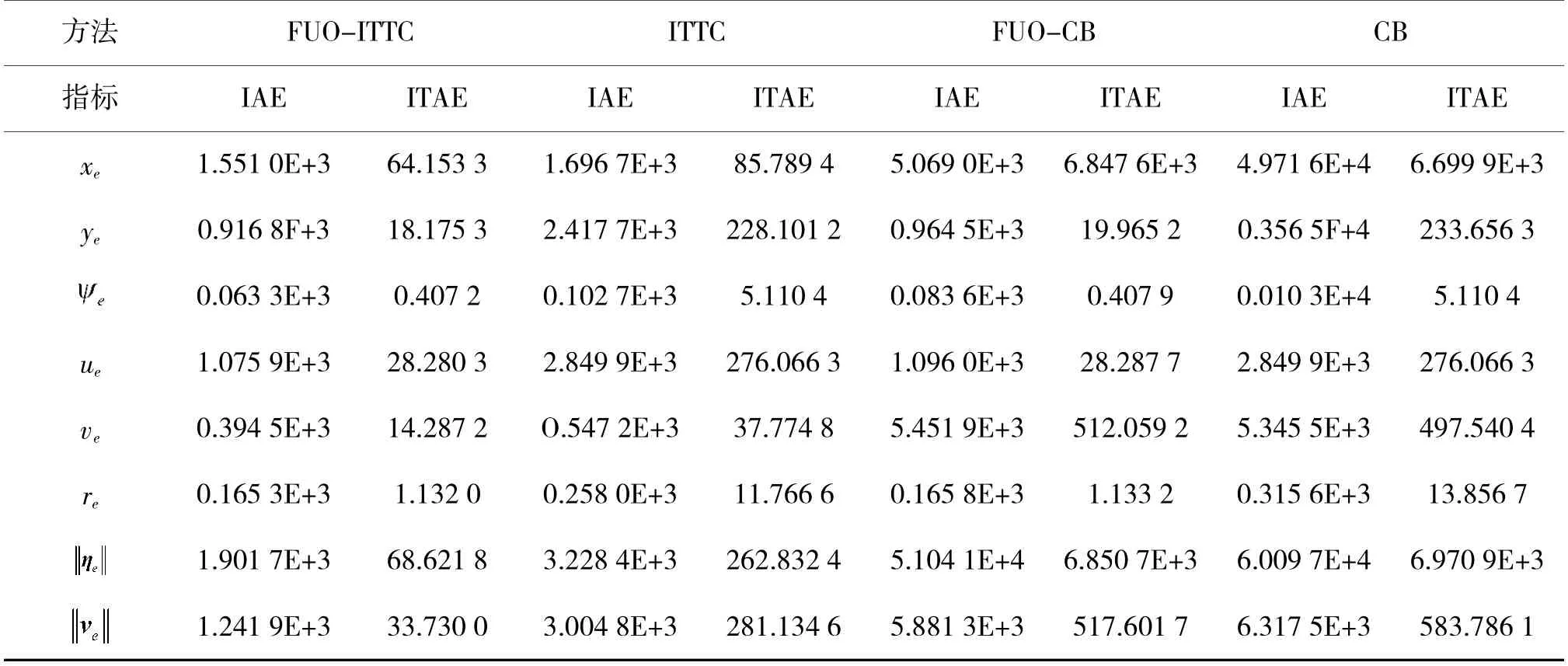
表4 轨迹跟踪性能比较（零动态）

表5 轨迹跟踪性能比较（渐进期望横摆角速度）

6 结论

为了提升跟踪精度与鲁棒性，有效解决欠驱动问题，提出了一种基于有限时间未知观测器的欠驱动水面艇交互式轨迹跟踪控制方法。在一个基准欠驱动水面艇上进行的实验可以证明如下结论：1）提出的方法能够准确地识别复杂的未知量，从而在提高轨迹跟踪性能；2）提出的方法即使在复杂未知情况下也能够使AUSV 精确地跟踪直线轨迹与渐开线螺旋控制扭矩，并且可以同时精确地实现位置跟踪和姿态保持；3）提出的方法对于可能出现的外部干扰和不确定性具有较强的鲁棒性，从而满足各种复杂条件下的控制要求。