移动机器人自适应轨迹跟踪控制*

马淑华，王锦华，马贤春，何 平

（1.东北大学秦皇岛分校控制工程学院，河北 秦皇岛 066004；2.暨南大学智能科学与工程学院，广东 珠海 519072）

0 引言

相较于传统工业机器人，轮式移动机器人具有体积小、自重轻、灵活性强、运动噪声低、工作环境多样化等特点，近年来被广泛应用于军事和工农业生产中，因此，其轨迹跟踪控制问题一直是广大科研工作者的研究热点。由于轮式移动机器人是典型的非完整约束系统，具有非线性、强耦合、外界干扰随机性等特点，使其高精度轨迹跟踪控制研究具有极大的挑战性。

针对移动机器人的轨迹跟踪控制问题，纵观国内外研究文献可知，主要的控制方法有：反演控制、滑模控制、预测控制、自适应控制等。Chwa针对二维极坐标运动的移动机器人，提出一种滑模控制方法，除了原点的小邻域之外，全局区域的参考轨迹都实现了渐近姿态的稳定和轨迹跟踪。Li等为解决移动机器人在轨迹跟踪控制中无法获得全球定位环境的问题，提出基于全向摄像头的视觉反馈自适应控制方法，针对机器人模型的参数进行在线调节。目前，常用相对笛卡尔坐标和相对极坐标两种局部位置表示方法对移动机器人的轨迹跟踪问题进行研究，其中，Miguel 等利用相对笛卡尔坐标，提出一种分布式控制方法来实现整个系统的全局稳定；Park 等在极坐标系下对移动机器人的轨迹跟踪问题进行研究。Yang 等设计了一种新型跟踪控制器，该控制器能够产生平滑连续的速度，驱动移动机器人实时跟踪路径。Sun 等针对领航者速度无法测量的问题，设计了一种基于神经网络的速度观测器来估计领航者的速度，实现了有限时间内的轨迹跟踪，但不能应用于没有通信的环境。为了消除测量噪声的负面影响，并且使跟踪控制方案适用于机器人之间没有通信的情况，Liang等提出了一种基于速度观测器的控制方案，实现了轨迹跟踪控制，但没有考虑到随机外部扰动的因素。Yang 等针对移动机器人受到外部干扰时的轨迹跟踪问题，提出了一种基于非线性干扰观测器的积分滑模控制系统，该方法能够很好地克服外部带来的非线性和不确定性，从而提高控制性能和鲁棒性。Chwa 等提出了一种基于自适应模糊输出反馈的轮式移动机器人同步位姿稳定和跟踪的控制方法，能够在运动和动态干扰下实现姿态稳定和跟踪控制。Luca 等提出了一种基于模型预测的控制方案，利用机器人状态反馈来适应运动过程中产生的扰动。Sharma 等提出一种新的控制方案，在完整和非完整移动机器人模型都受到外部干扰的情况下，实现多个简单连接的机器人在确保连通性和避免碰撞的同时保持稳定。Wang 等针对一系列遭受不可预测时变干扰的非线性系统，提出了一种鲁棒有限时间输出反馈的控制方法，利用有限时间状态观测器提供的状态估计控制闭环系统的稳定性。

1 问题描述

研究对象是4 轮结构移动机器人，如图1 所示，其中，R为领航机器人，R为跟随机器人。2 个后轮为驱动轮，通过调节各自驱动电机的输入电压形成差速来实现车体位置和角度的变化，2 个前轮为随动轮，仅起支撑车体的作用。本文采用笛卡尔坐标系，XOY 是全局坐标系，xoy 是以移动机器人自身为参考系的局部坐标系，选取移动机器人的质心点为参考点。领航者R的运动学模型如式（1）所示。

图1 移动机器人运动学模型

其中，r=（x，y）表示领航者R在全局坐标系中的位置；θ表示领航者R前进轴方向与X 轴的偏转角度；v与ω分别为领航者R的实际线速度与实际角速度。

跟随者R的运动学模型表示为：

其中，r=（x，y）表示跟随者R在全局坐标系中的位置；θ表示跟随者R前进轴方向与X 轴的偏转角度；v与ω分别为跟随者R的线速度与角速度；d 为未知时变外部扰动。

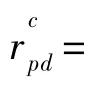
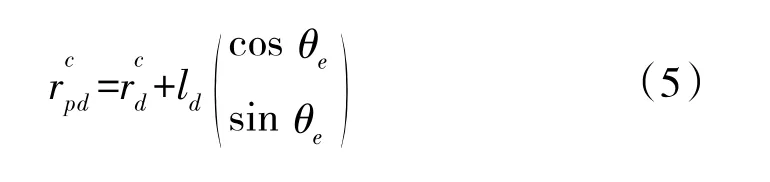
其中，l表示参考点P在前进轴方向的偏移量。对式（5）求导得：

2 控制器设计

在实际应用中，领航者速度在测量时存在噪声影响，导致其无法精确测量。因此，本文在领航者速度无法精确测量的基础上，考虑跟随者受到未知扰动的情况，分析移动机器人的运动学模型，提出基于运动学特性的轨迹跟踪控制器设计。

2.1 恒定速度

当领航者速度（v，ω）无法测量且为恒定值时，速度观测器设计为：

其中，K为对称正定矩阵。

将式（14）代入式（6）可得：

在设计控制器时，需要保证整个观测器-控制器闭环系统的稳定性，即移动机器人的观测器估计误差和跟踪误差均为收敛，利用Lyapunov 稳定性判据对系统的稳定性进行判断。

假设1：未知扰动信号d 是有界的，即|d|≤b，|d˙|≤b，其中，b、b是大于零的常数。

定理1：由一对领航-跟随机器人构成的轨迹跟踪控制系统，领航者速度为常数，使得0＜v＜∞和|ω|＜∞，初始时刻的相对方向满足条件|θ（0）|＜π。当领航者速度为恒定值时，针对式（15）描述的误差动态方程，若跟随机器人采用的控制器为式（8）、式（9）、式（12）和式（14），则当t→∞时，r收敛到原点小邻域内。

证明选取Lyapunov 函数为：

对式（16）求导并将式（15）代入可得：

将式（10）、式（11）和式（13）代入式（17）可得：

通过假设1 可得：

式（18）可进一步写成：

2.2 时变速度

当领航者速度（v，ω）为时变的情况下，速度观测器设计为：

其中，σ和σ表示大于零的常数。则其导数为：

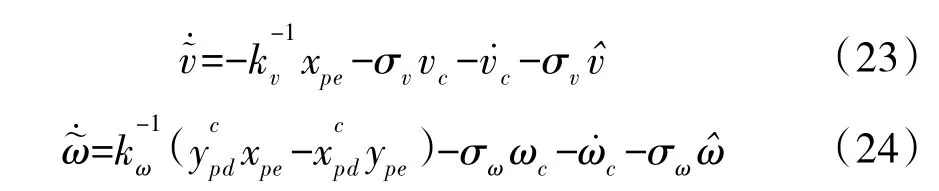
假设2：领航者的速度是有界的，即|v|≤b，|v˙|≤b，|ω|≤b，|ω˙|≤b，其中，b、b、b、b是大于零的常数。

定理2：当领航者速度为时变值时，针对式（15）描述的误差动态方程，若跟随机器人采用的控制器为式（12）、式（14）、式（21）和式（22），则当t→∞时，r收敛到原点小邻域内。

证明 选取Lyapunov 函数为式（16），将式（23）、式（24）和式（13）代入式（17）可得：

通过假设1 和假设2 可得：

进一步写成：

综上所述，在速度观测器和扰动观测器的基础上，结合移动机器人的运动学模型设计轨迹跟踪控制器，使跟随者在指定轨迹上进行跟踪，有效提高移动机器人的轨迹跟踪精度。

3 系统仿真及分析

为验证该控制方法的有效性，在Matlab 中进行仿真实验。选取1 台领航者与1 台跟随者来实现轨迹跟踪控制，分别对恒定速度和时变速度下圆形轨迹跟踪进行仿真。

图2 恒定速度控制输入

图3 恒定速度估计误差收敛曲线

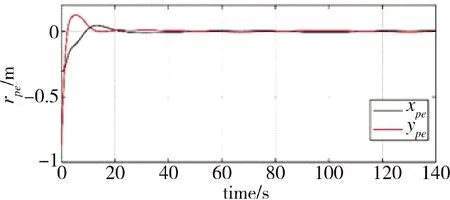
图4 恒定速度跟踪误差收敛曲线

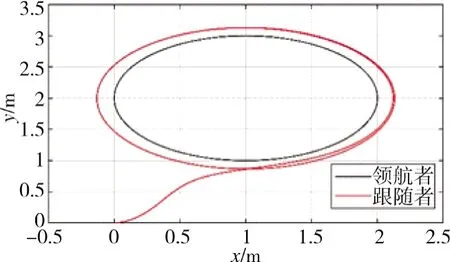
图5 恒定速度轨迹跟踪曲线

由仿真结果可知，在领航者速度恒定的情况下，跟随者虽然在运动过程中受到扰动作用，但是在轨迹跟踪控制算法的作用下，领航者的线速度和角速度以及未知扰动的观测估计误差都收敛到有界范围内，且实际的运动轨迹在目标轨迹附近波动，即跟踪误差收敛到原点的小邻域内，可以通过选择较大的控制增益，使跟踪误差根据需要变小。

仿真2：领航者的时变速度设置为v=0.1-0.02 cos（0.1t）m/s，ω=0.1-0.02cos（0.1t）rad/s。时变外部扰动设置为d=0.01sin（0.1t）m/s。跟随者的观测器参数分别为：K=0.7I，k=0.1，k=0.6，k=0.3，σ=0.01，σ=0.01，σ=0.5。在领航者速度时变的情况下，由式（12）、式（14）、式（21）和式（22）给出方案的仿真结果如图6～图9 所示。

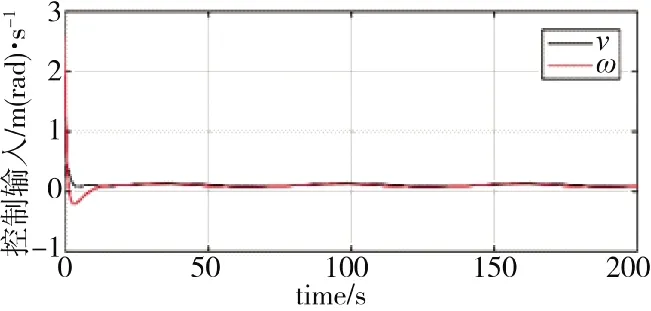
图6 时变速度控制输入

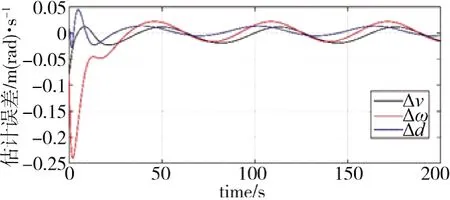
图7 时变速度估计误差收敛曲线

图8 时变速度跟踪误差收敛曲线

图9 时变速度轨迹跟踪曲线

由仿真结果可知，在领航者速度时变的情况下，领航者的线速度和角速度的估计误差、未知扰动的观测估计误差以及跟随者的跟踪误差相对于恒定速度时的误差要大，但最终还是收敛到有界范围内，使其实际的运动轨迹在目标轨迹附近波动。

4 结论

本文针对移动机器人跟随者受到未知扰动影响时的轨迹跟踪控制问题，提出一种基于估计扰动前馈补偿的轨迹跟踪控制方案，实现了在未知扰动作用下能够跟踪目标轨迹的控制效果。通过选择较大的控制增益，使跟踪误差根据需要变小。仿真结果验证了所设计控制方法的有效性。